我国未来十年基尼系数的预测及政策建议——基于灰色预测模型的分析

胡江霞 罗玉龙 杨孝良

(1.重庆工商大学长江上游经济研究中心 重庆 400067；2.重庆三峡职业学院经贸系 重庆万州 404155)

我国未来十年基尼系数的预测及政策建议
——基于灰色预测模型的分析

胡江霞1,2罗玉龙2杨孝良1

(1.重庆工商大学长江上游经济研究中心 重庆 400067；2.重庆三峡职业学院经贸系 重庆万州 404155)

本文运用灰色理论建立我国居民收入基尼系数的灰色预测模型，同时运用该模型对未来10年的中国基尼系数进行了预测。结果表明：未来10年中国的基尼系数基本呈现逐年递减的趋势。最后，本文从狠抓发展这个环节，扶持现代农业、切实增加农民收入，实施若干强有力的惠民政策和加大教育支出四个方面,提出了相应的建议。

居民收入；基尼系数；灰色预测模型；预测

基尼系数(Gini Coefficient)是意大利经济学家基尼于1922年提出的，它是现行较为通用的衡量一个国家收入分配差距的重要指标。基尼系数在0.25以下为平等程度较高状态，在0.3—0.4之间为正常差距状态，超过0.4为警戒状态，接近0.6则属于高危状态。[1]目前，国际上用来分析和反映居民收入分配差距的方法和指标很多。基尼系数由于可以定量的反映居民之间贫富差异程度，可以较客观、直观地反映居民之间的贫富差距，预报、预警和防止居民之间出现贫富两极分化，因此得到了世界各国的广泛认同和普遍采用。

灰色系统是既含已知信息又含未知信息的非确定的信息系统。灰色系统理论认为，系统是否会出现信息不完全的情况,主要取决于认识的层次、信息的层次以及决策的层次。对于城乡居民收支样本数据的采集以及基尼系数的计算，在中国统计系统中始终进行。由于原始数据的获取难度较大，加上各个统计口径的差异等等因素的制约，大大增加了基尼系数估算的难度。一直以来国家统计局都未正式公布我国居民收入的基尼系数，直到2014年1月国家统计局才公布了2003年至2012年全国居民收入基尼系数，这说明，关于基尼系数测算问题实际上是一个灰色系统问题。灰色系统理论认为，对既含有已知信息又含有未知或非确定信息的系统进行预测，就是对在一定方位内变化的、与时间有关的灰色过程的预测。尽管过程中所显示的现象是随机的、甚至是杂乱无章的，但是这些数据序列具有其潜在的规律。灰色预测就是利用这种规律建立灰色模型，对数据之间潜在的规律进行预测。本文运用灰色预测模型，对我国未来10年的居民收入的基尼系数进行预测，以期为有关部门今后制定调节收入分配差距的政策提供参考依据。

一、文献综述

王惠文、龙文、赵江涛[2](2003)利用洛伦兹曲线计算出基尼系数，并在成分数据预测建模方法的基础之上，提出洛伦兹曲线的预测模型，利用北京市城八区的人口和GDP数据，对城八区经济发展的不平衡趋势进行了预测，结论表明北京城八区的经济发展是不平衡的。陈昌兵[3](2007)利用非参数计量经济模型中的分布密度函数估计方法，分析了1995—2006年城乡居民基尼系数变化特征，并且对我国各地区居民的平均收入水平与城乡居民收入平均基尼系数进行判别分析。徐剑、吴广谋[4](2007)基于历史数据，采用适用控制理论中的多层次递阶方法建立了模型，对江苏省的基尼系数变化趋势进行了预测。杨竹莘[5](2007)利用灰色预测模型，得出2005年基尼系数的预测值为0.471。2010年，中国的基尼系数可能临近0.5，进而得出结论：中国的基尼系数仍然是逐年攀升的，进而分配差距的扩大也是逐渐扩大的。王祖祥、张奎、孟勇[6](2009)采用城乡收入分配统计分布的构造方法，利用《中国统计年鉴》(1995—2005)的收入分配数据估算了我国的基尼系数，结论表明：我国目前城乡两大部门内部的基尼系数都不大，都没有超过0.34，但是从2003年开始，我国加总的基尼系数已经超过0.44。张焕、王铮[7](2010)通过对中国基尼系数的理论分析和实证研究，发现我国的城镇化过程主导着我国基尼系数的变化，并且指出当前我国基尼系数的发展已经接近或达到U型曲线顶点的水平，我国最早在2005年，最晚到2010年，基尼系数开始下降。张君施[8](2010)首先以动态的方式，利用线性拟合方程，拟合并预测了我国居民的基尼系数，并详细阐述了基尼系数变动的趋势；其次，从历史的、政策的角度，分析了我国基尼系数过高的原因；最后，作者指出要结合我国的国情，充分利用政策优势，改善城乡收入分配格局，缩小城乡间的收入差距，使我国居民收入差距处于合理的范围，处在库兹涅茨的倒U型的左半部分。史王民[1](2013)采用时间数列灰色预测模型，对我国的基尼系数进行了估算，预测出2007—2010年4年的基尼系数分别是0.5075、0.5265、0.5463、0.5668。

纵观上述研究，在研究内容上，研究者主要从以下两个方面来分析：第一，从全国、区域或某一城市三个方面研究基尼系数，如杨竹莘(2007)，徐剑、吴广谋(2007)；第二，在研究方法上，研究者主要用多种计量方法来研究基尼系数,如非参数计量模型、线性拟合方程、洛伦兹曲线的预测模型等等。尽管大多数研究者从多个角度阐述了基尼系数，但是由于获取的数据口径的差异，所预测的基尼系数存在较大的差异，因此预测出的基尼系数在某种程度上难以科学地反应我国居民收入水平的客观差距。本文利用国家统计局公布的较为权威的基尼系数，采取灰色理论，从动态角度建立我国居民收入基尼系数的灰色预测模型，通过本研究能够更加科学的对我国基尼系数进行预测。

二、灰色预测模型的建构

灰色预测模型是于1982年由邓聚龙教授提出来的，该理论提出之后在学术界引起了很大的反响，该方法被很快地运用于各类学科。[9]灰色预测理论主要是通过鉴别系统中各个因素之间发展趋势的相似程度，做灰色关联度分析，并通过对原始数据的累加生成新的数列，最后运用新的数列建立相应的微分方程模型，从而预测研究对象未来的发展趋势。[10]本研究主要采用GM(1,1)灰色预测模型，建立灰色预测模型的步骤如下：

1.构建GM(1，1)原始数据序列。

按照所要预测的各项指标的原始数据如下：

X(0)(K)={X(0)(1),X(0)(2),X(0)(3)……X(0)(n)}

(1)

式中K=1,2,3…n,X(0)(1),X(0)(2),X(0)(3)…X(0)(n)为原始数据系列中的各个数字。

2.构建GM(1，1)累加生成序列以及微分方程。

第一步，灰色生成。具体计算方法：对原始数据累加生成下式：

第二步，建立GM(1,1)的微分方程。式子如下：

(3)

3.运用最小二乘法求解参数向量a和u,计算方法如下：

(4)

4.建立时间响应函数，其微分方程如下：

(5)

5.建立GM(1，1)预测模型。通过求导还原可以得出预测模型如下：

(6)

6.模型的精度检验。

残差检验：

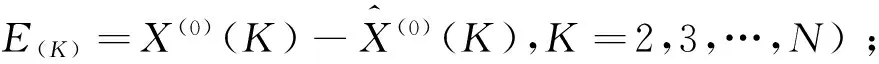
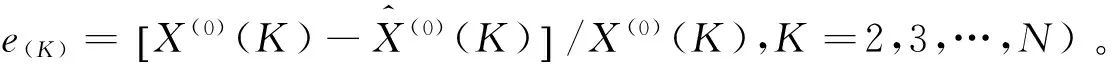
三、数据说明

2014年1月国家统计局公布的我国2003年至2012年全国居民收入基尼系数分别为：2003年是0.479，2004年是0.473，2005年是0.485，2006年是0.487，2007年是0.484，2008年是0.491。然后逐步回落，2009年是0.490，2010年是0.481，2011年是0.477，2012年是0.474。

四、实证分析

本部分主要根据国家统计局公布的2003—2012年10年间全国居民收入的基尼系数，建立了基尼系数的灰色预测模型。其研究框架如下：

(一) 构建原始数列

建立灰色预测模型的第一步，就是构建原始数列，具体数据参见表1。

表1 2003—2012年国家统计局公布的全国居民收入基尼系数

(二) 构建累加的生成数列

将表1中的全国居民收入基尼系数作为原始数据序列，累加构建新的数列：

原始数据系列：X(0)(t)={0.479，0.473，0.485，0.487，0.484，0.491，0.490，0.481，0.477，0.474}

累加生成的数列：X(1)(t)={0.479，0.952，1.437，1.924，2.408，2.899，3.389，3.870，4.347，4.821}

(三) 计算灰数a,内生控制灰数u

第一步，利用累计生成数列和原始数列分别构建矩阵B以及数据向量Yn:

第二步，计算BTB，(BTB)-1，BTYn:

第三步，利用最小二乘法计算参数向量a和u,计算方法如下：

将上面计算的(BTB)-1，BTYn的值代入公式4：

因此，a=0.000892,u=0.4848。

(四) 构建灰色预测模型

将a,u的值代入公式6，可以得出：

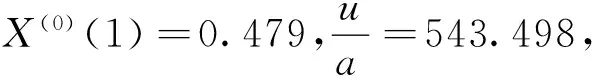
-543.019e-0.000892k+ 543.498

从而得出灰色预测模型为:

(五)模型的验证

首先按照上述建立的预测模型，求出X′0(K)数列，再与原始数列X0(K)计算绝对残差E(K)=X′0(K)-X0(K)，以及相对残差β=[E(K)/X0(K)]·100%，计算数值参见表2。由于本文篇幅有限，具体计算过程详见史王明[1](2013)、刘静暖[11](2013)，对于本模型的残差检验在此省略。通过计算可知绝对残差为0.0003，相对残差为1.0425%，这表示该模型的预测精度好。

表2 灰色预测模型的预测精度检验

(六) 未来10年的基尼系数的预测分析

根据建立的灰色预测模型，预测我国未来10年基尼系数的走向，详情参见表3。

表3 2013—2022年我国居民收入基尼系数的灰色预测

五、结论及政策建议

(一) 研究结论

1.本文运用灰色系统理论建立了灰色预测模型。灰色预测模型经过精度检验后，发现该模型的预测精度好，这说明本研究建立的灰色预测模型能够较好地预测我国居民收入的基尼系数。

2.本文运用灰色预测模型对我国近十年来的全国居民收入水平的基尼系数进行测算。从表3显示的未来10年我国基尼系数的走向来看，我国未来10年的基尼系数呈现是逐年递减的状态0.4803>0.4799>0.4794>0.4790>0.4786>0.4782>0.4777>0.4773>0.4769>0.4765,这表明随着经济的发展，我国城乡收入水平之间的差距将逐步趋向合理化，居民之间收入水平的差距会越来越小。但是，从表3中我们可以看到未来10年的基尼系数尽管是逐年下降的，但是下降幅度并不是很大，如2022年的基尼系数相比2013年而言，仅仅下降了0.0038，,而且未来10年的基尼系数均高于0.4，超过了国际警戒水平。这说明我国未来10年基尼系数稳中有降，但是从总体而言，我国居民收入水平的差距还是较大的。

3.如何将多种计量方法相结合，通过对比分析，更加科学地预测我国居民收入的基尼系数，这是后续研究要进一步努力的方向。

(二)政策建议

根据上述研究结论，我们可以看出我国居民收入的基尼系数在未来10年之内仍然高于国际警戒水平0.4，但是从总体而言呈现逐年下滑的趋势，笔者认为要想保障这种良性的趋势，政府必须实行一系列强有力的措施，改善居民收入水平，从而缩小城乡收入水平之间的差距。

1. 狠抓发展这个环节。切实提高国民的收入水平，必须狠抓发展这个环节。只有经济发展了,蛋糕做大了，才能为实现公平分配、缩小贫富差距打下牢固的物质基础。我国是一个典型的“二元”经济社会，农村和城市经济发展水平存在较大的差异。正是基于这样的现状，目前我们应该要特别重视农村经济的发展, 促进二元经济向现代经济的转换。只有加速这一进程, 才能为缩小城乡收入差别、地区收入差别创造必要的条件。只有把重视农村经济的发展要提到战略的高度来认识，才能为维持社会稳定提供重要前提。

2. 扶持现代农业，切实增加农民收入。我国是一个农业大国，农民人口占了绝大多数。因此，切实提高农民的收入，要想缩小城乡收入差距，必须扶持现代农业，切实增加农民收入。从世界范围来看，建立现代农业是大势所趋，我国农业只有从传统的农业生产方式向现代农业转型，才能不断提高农业生产效率，从而增加农民收入。发展现代农业的途径有：(1)增加对农业基础设施的投入力度，同时加快农业科技的研发和推广，发展高效特色生态农业；(2)加大对农民生产技能以及经营管理能力的培训，培养一批懂耕作、会经营的新型职业农民；(3)切实增加农民收入，逐步提高农作物价格，建立合理的价格形成机制，推动农产品流通渠道的多元化；(4)加快农村土地的流转，实现规模化经营；(5)进一步优化农村经济结构,提升农产品价值,拓宽农民就业渠道,提高农民政治地位和强化对农民的公共服务等。[12]

3. 实施若干强有力的惠民政策。政府要实施若干强有力的惠民政策，增加国民的收入，这样才能促进社会的和谐发展。重点实施以下惠民政策：(1)个人所得税政策。政府要大力实施个人所得税政策，大力调节高收入者与低收入者之间的差别。这是缩小高收入阶层同一般人之间收入差距的一项重要政策措施。为了发挥这一政策的作用, 首先要提高收入的透明度, 其次还要让人们乐于接受。(2)社会保障政策。社会保障政策要向农村重点倾斜。这是解决因失业、疾病以及年老等原因所造成的贫富分配不均的最重要政策措施。(3)实行宽松的劳动力流动政策。在国家对城乡劳动力流动采取比较宽松的政策的情况下，农村劳动力向城镇的流动就不可避免。城乡发展的差距越大，农村劳动力向城市流动的愿望就越强烈，这样大量富余的农村的劳动力大量流入城市，不仅可以实现农民增收，而且是促进产业结构调整，建设社会主义新农村的重要途径。(4)实施积极的就业政策。政府要积极调整就业政策，包括清理和取消各种针对农民工进城就业的歧视性规定，如对企业使用农民工的内政审批和行政收费，规定不得以解决城镇劳动力为由清退和排斥农民工。要将农民工纳入城市的公共服务体系，让农民工在就业服务、子女教育、居住以及疾病预防等公共服务方面享受与城镇居民同等的待遇。(5)实施积极的金融政策。在金融发展方面应积极发挥金融在农村经济增长中所起到的作用与力量，促进更多的金融资本为农村社会发展与建设提供资金支持。[13]

4. 加大教育支出。根据福利经济学的观点，直接转移支付对于缩小贫富差距的效果并不是很理想，无法发挥乘数效应的作用。与直接补偿低收入者相比，更加合理的方式就是加大教育投入力度，不断提高劳动者的素质，这样才可以提高其收入水平，从而缩小贫富差距。因此，政府应不断加大教育投入力度，提高劳动者的整体受教育程度，切实提高劳动者的素质，这样才能满足未来产业升级对人才的需求。只有这样，才能逐步缩小我国居民之间的贫富差距。

[1] 史王明.基于基尼系数的时间灰色预测模型[J].统计与决策，2013(3)：17-20.

[2] 王惠文，龙文，赵江涛.基尼系数的预测建模方法及在北京市经济发展分析中的应用[J].系统工程，2003(21)：11-18.

[3] 陈昌兵.各地区居民收入基尼系数计算及其非参数计量模型分析[J].数量经济技术经济研究，2007(3)：21-25.

[4] 徐剑，吴广谋.基于历史数据的江苏省基尼系数变化趋势预报——采用多层递阶方法对江苏区域经济差异的模型分析[J].价值工程，2007(10)：68-73.

[5] 杨竹莘.中国收入分配差距预测的GM(1，1)模型[J].数学的实践与认识，2007(37)：33-39.

[6] 王祖祥，张奎，孟勇.中国基尼系数的估算研究[J].经济评论，2009(3)：54-58.

[7] 张焕，王铮.中国基尼系数预测及分析[J].数量经济技术经济研究，2010(4)：12-17.

[8] 张君施.基尼系数理论在我国的适用性[J].北京工商大学学报(社会科学版)，2010(2)：48-52.

[9] 胡江霞,罗玉龙，郑宏伟.职业教育经费投入与区域经济发展的灰色关联分析[J].教育学术月刊，2013(10)：20-24.

[10] 邓聚龙.灰色预测与决策[M].武汉：华中理工大学出版社，1990.

[11] 刘静暖，黄林，刘宇.基于灰色模型的碳减排压力分析[J].工业技术经济，2013(3)：150-155.

[12] 于代松.推进城乡一体化,建立农民增收长效机制——对成都地区农民增收的调查与分析[J].西华大学学报(哲学社会科学版),2005(2):30-33.

[13] 刘吕吉,郑理.开放经济视角下的金融发展对城乡收入差距的影响[J].西华大学学报(哲学社会科学版),2013(3):84-89.

[责任编辑 谭金蓉]

2014-10-20

本文获得国家社科基金青年项目(14CJL031)的资助。

胡江霞(1980—)，女，重庆工商大学博士研究生，重庆三峡职业学院经贸系讲师，研究方向为区域经济学。

F126

A

2095-1124(2015)01-0044-06