平板折叠桌的动态过程分析与参数的优化设计

吴丹丹朱家明

（安徽财经大学统计与应用数学学院　安徽蚌埠　233030）



平板折叠桌的动态过程分析与参数的优化设计

吴丹丹朱家明

（安徽财经大学统计与应用数学学院安徽蚌埠233030）

摘要：针对平板折叠桌动态变化过程中各参数，使用轨迹方程分析、非线性规划以及对比分析等方法，构建折叠桌动态变化和基于非线性规划的优化设计模型，使用Lingo、Matlab等软件编程，分别研究了：定量描述已知平板尺寸折叠桌的动态变化，桌角边缘线形状并求得每根木板的空槽长度；对于指定部分尺寸的平板桌确定最优加工参数和平板大小，使得产品稳固性好、加工方便并且用材最少。

关键词：平板折叠桌；优化模型；非线性规划；Lingo；matlab7

创意平板折叠桌（RisingSideTable）是Rising系列的最新作品（立体结构变化过程[1]见图1），此款折叠桌的平板尺寸为120cm×50cm×3cm，每根木条宽2.5cm，连接桌腿木条的钢筋固定在桌腿最外侧木条的中心位置，折叠后桌子的高度为53cm。经过之前的设计实验，这件作品更注重于表达木制品的优雅和设计师所想要强调的自动化与功能性[2]。为了增大有效使用面积，设计师以长方形木板的宽为直径截取了一个圆形作为桌面，又将模板剩余的面积切割成了若干个长短不一的木梁，每个木梁的长度为宽到圆上一点的距离，分别用两根金属棒贯穿两侧的木条，使用者只需提起木板两侧，便可以在重力的作用下达到自动升起的效果。

一、平板折叠桌动态变化的定量分析

（一）桌腿端点运动轨迹。根据所给数据，运用勾股定理，可求得木板尺寸表，如表1所示。

表1　木板尺寸表

图1　折叠桌立体结构变化图

简化结构以其中某一根木条BD为例探究其与最外侧木条的动态变化关系，在折叠过程中，当BD与水平面的夹角θ小于90度时运动状态主视图见图2。其中最外边木条记为OA,B为BD的转轴位置，C为钢筋与OA固定处。则BD的运动状态与最外侧木条由如下关系:

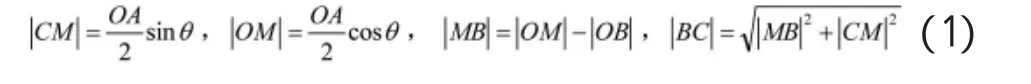
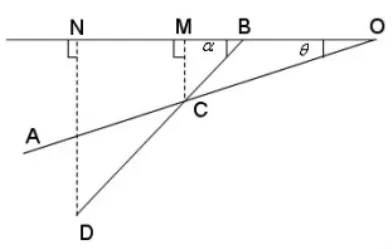
图2　折叠桌木板主视图

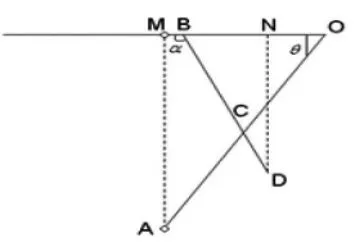
图3　折叠桌木板主视图

当BD与水平面的夹角大于90度时运动结构见图3，由（1）（2）式知，MB，NB小于0，即（3）式恰好也符合夹角α是钝角时的计算方向，故当0≤θ≤θmax，y有统一的计算公式。

由于整个桌子关于桌面中心点完全对称，所以，只考虑左下角部分的十根木条端点的坐标与θ的关系即可描述该动态折叠过程。为最外侧木板的长度,

运用matlab软件[3]做在此区间做每根木条划过的轨迹见图4。

图4　每根木条划过轨迹图

（二）相关参数的求解。

当θ=θmax时，即平板桌站立时：

2.木条端点坐标。结合（4）式计算该状态下桌脚边缘的坐标，10根木条的底端坐标与空槽长度(w)，如表2所示。

表2　木条端点坐标与卡槽长度值表

二、平板折叠桌的优化设计

（一）设计思路。根据上述对平板折叠桌动态变化过程的分析，对于桌高70cm，桌面直径80cm的情形，确定最优设计加工参数。例如，平板尺寸、钢筋位置、开槽长度等。并满足折叠桌的设计应做到产品稳固性好、加工方便、用材最少的条件。

（二）平板折叠桌设计模型。

1.参数设置。做出片板折叠桌的简图，如图5、图6所示。

图5　折叠桌俯视图

图6　折叠桌侧面示意图

图5表示，设计参数包括平板尺寸：a（长）×b（宽），此处不考虑平板的厚度。每根木条的宽度为d，所截木板个数为n，钢筋的位置表示为钢筋与最长边转轴的距离x，桌面两侧直线面的距离为s，开槽长度为w。

由图5,图6中关系可知：

2.条件分析。

(1)产品稳固性要求。由模型的准备，假设桌子的质量的分布是均匀的，故若要使桌面能承重，假设在桌面的边缘放置重力为G的物体，若此时的重心也偏移到桌面边缘，要使得桌面不发生倾翻，支撑面至少包含桌子的边缘。由力矩平衡，可知，

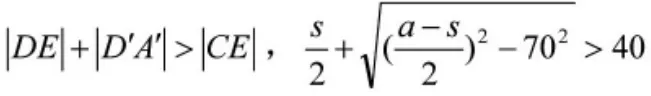
而且桌面两侧直线面的距离为s不能为0，因为桌脚对桌面有向上的支撑力，而且s在满足支撑面与稳定性的关系的条件下，s值越大越好。由第一题的近似，2d可作为s的下限，设定S0为s的上限。即满足S0叟s叟2d，

(2)加工方便要求。若要满足加工方便，则使木条的个数n尽量小，但是为了体现美观，要使桌面呈现一个类似的圆形，此时n满足一定的条件，即n大于一定的量，此处设为N0，即n≥NO。另开槽长度越小则加工越方便，即w越小越好。

在后续的分析中可以设N0=5,10,20,30,40，并对最终的结果进行比较。

(3)用料要求。用料最少即minab。根据(1)(2)(3)，可建立非线性规划模型[4]:minab

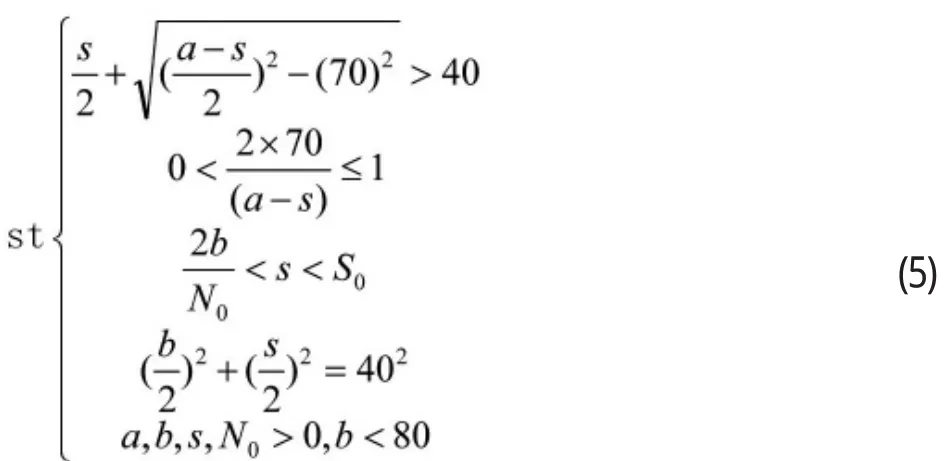
非线性参数方程中没有约束的条件，故设置来计算分析

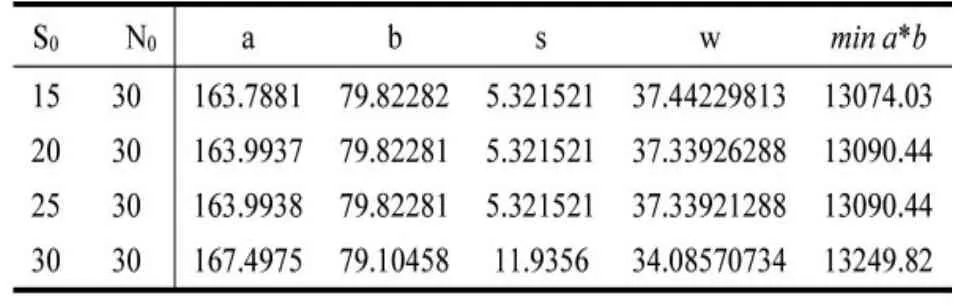
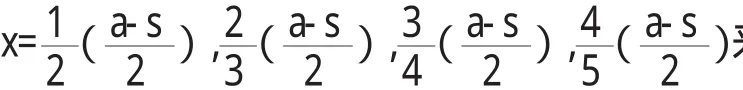
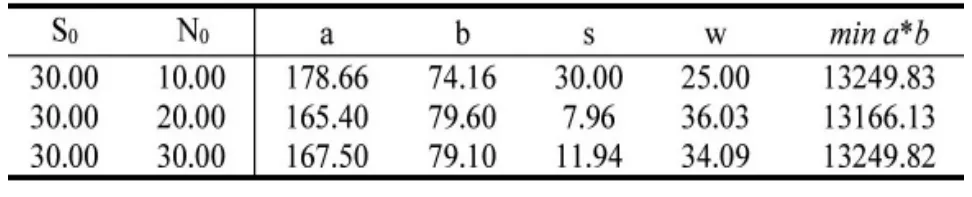
由表4可知，当设置不同的N0时，可见w随N0的变化增大而增大，minab随N0的变化的增大而减小，但是为了加工方便，w越小越好，而minab也越小越好，故对于不同的N0无法同时满足两个条件，根据实际情况，选取N0为20时有最优的参数。

表5　S0,N0固定时部分参数表（单位/厘米）

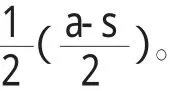
综上所述，最优的平板尺寸为长a=165.3974cm，宽b=79.60299cm，每根木条的宽度为d=4cm，所截木板个数为n=20，钢筋的位置表示为钢筋与最长边转轴的距离x=39.3593cm，桌面两侧直线面的距离为s=7.960299cm，开槽长度为w=31.79611cm。

三、总结

本文首先对给定平板折叠桌进行参数和运动过程的定量分析[5]，并利用其运动的数学规律通过非线性规划的方法建立了平板桌设计的优化模型，结论中应用对比分析法，综合考虑了用料以及性能的要求，以达到平板桌优化设计的目的。

参考文献：

[1]涂晶洁.机械制图[M].北京:清华大学出版社,2010.

[2]巩斌.基于随机前沿法上市商业银行产出效率的实证分析[J].绥化学院学报,2013(12).

[3]张贤明.MATLAB语言及应用实例[M].南京:东南大学出版社,2010.

[4]洪文,冯守平,吴本中.利用LINGO建立最优化模型[M].长春:吉林大学出社,2005.

[5]杨桂元,朱家明.数学建模竞赛优秀论文评析[M].合肥:中国科学技术大学社,2013.

[责任编辑郑丽娟]

中图分类号：TB11

文献标识码：A

文章编号：2095- 0438（2015）06- 0148- 03

收稿日期：2015-02-20

作者简介：吴丹丹（1984-），女，安徽潜山人，安徽财经大学统计与应用数学学院学生，研究方向：信息与计算科学；朱安明（1973-），男，安徽泗县人，安徽财经大学统计与应用数学学院副教授，硕士，研究方向：应用数学与数学建模。

基金项目：国家自然科学基金项目（11301001）；安徽财经大学教研项目（acjyzd201429）。