型钢混凝土纯扭构件极限扭矩计算理论研究

丁双双，邵永健，宋学强

(苏州科技学院 土木工程学院，江苏 苏州 215011)

型钢混凝土纯扭构件极限扭矩计算理论研究

丁双双*，邵永健，宋学强

(苏州科技学院 土木工程学院，江苏 苏州 215011)

在现有钢筋混凝土纯扭极限扭矩计算公式的基础上，基于叠加原理，对H型钢混凝土纯扭构件的极限扭矩计算公式进行了初步研究，提出了型钢混凝土纯扭构件的受扭承载力计算公式，并将计算值与试验值进行比较，计算值与试验值符合良好。比较了开口截面与闭口截面型钢的抗扭性能，结果表明在抗扭性能方面，闭口截面比开口截面具有很大的优越性。

型钢混凝土；纯扭构件；极限扭矩计算

0 引言

型钢混凝土结构中的钢筋混凝土对型钢提供侧向支撑，使型钢的稳定性得以提高；型钢使部分钢筋混凝土处于双向甚至三向受压，能够充分发挥混凝土抗压强度。可见，型钢混凝土结构充分发挥了两者的优势，取长补短，具有承载力高、刚度大、延性耗能好等优点。可是时至今日，我国型钢混凝土结构设计规程[1-2]尚无有关受扭承载力计算的相关条文规定。

近年来，伴随着结构形式与种类的不断创新，工程抗震要求的提高，出现了大量的受扭问题亟待解决。因此，对型钢混凝土构件受扭承载力的研究是理论发展的需要，也是工程应用的需要。

1 H型钢混凝土构件在纯扭作用下的极限扭矩的计算

型钢混凝土构件的极限扭矩，按外部的钢筋混凝土承担的扭矩和内部的型钢承担的扭矩相互叠加计算。

1.1 钢筋混凝土承担的极限扭矩

我国《混凝土结构设计规范》(GB50010-2010)是基于变角空间桁架模型计算钢筋混凝土构件的极限扭矩。为与我国规范相统一，取钢筋混凝土的极限扭矩计算公式如下：

(1)

式中各项符号意义详见参考文献[3]。

1.2 型钢部分承担的极限扭矩

轧制H型钢一般均属于薄壁杆件，因此可以运用薄壁构件的相关理论分析。实际工程中，扭转问题都为约束扭转，扭矩可以分为自由扭矩Ts和Tw翘曲扭矩两部分叠加。一端固定的H型钢在自由端作用有扭矩Tp的受力情况如图1所示。

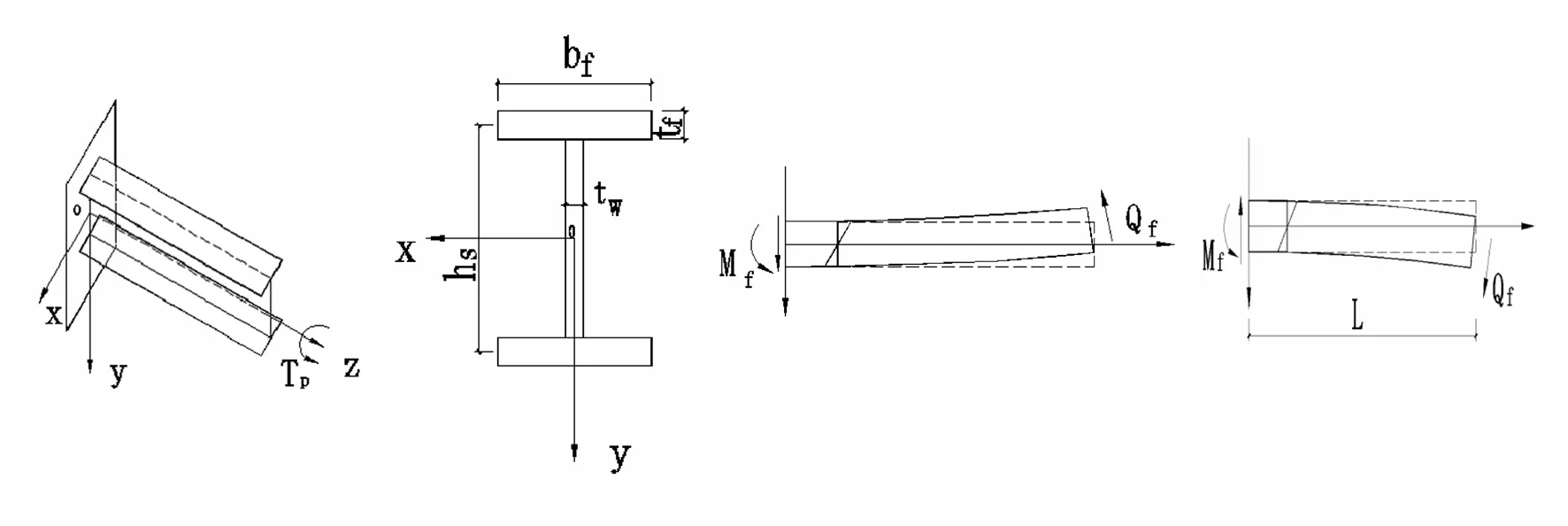
(a)约束扭转 (b)截面尺寸 (c) 上翼缘变形 (d)下翼缘变形

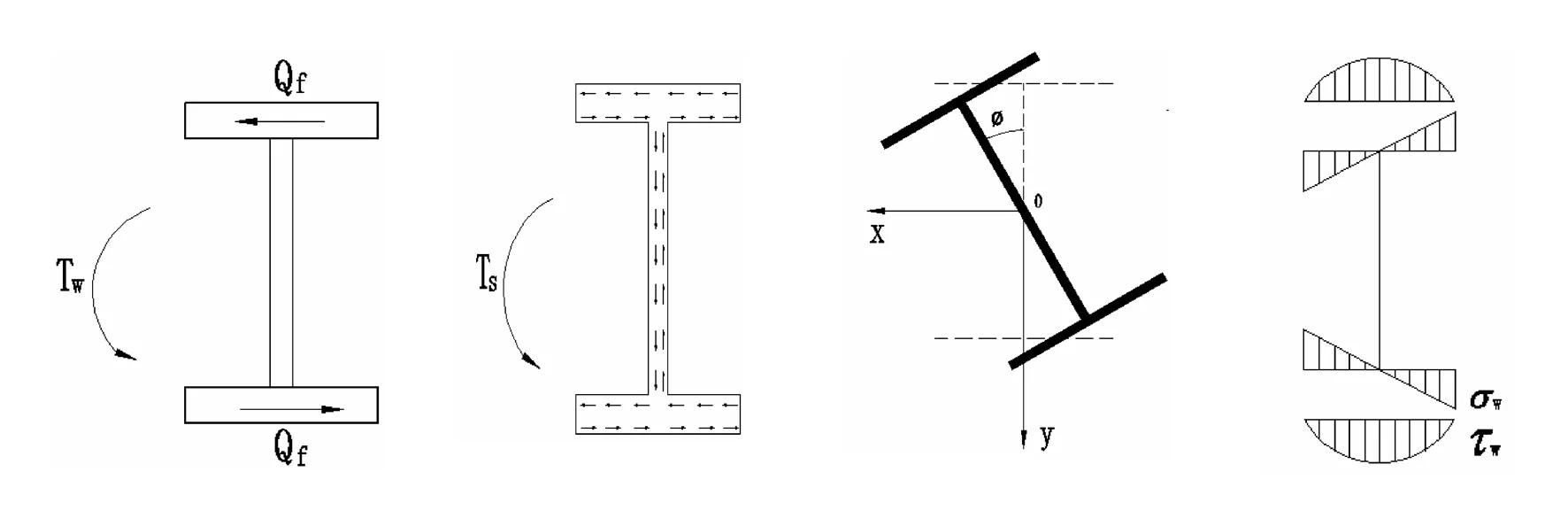
(e)Tw的产生 (f)自由扭矩Ts产生剪力流 (g)扭转角φ(h)τw和σw的分布

外力产生的扭矩Tp，由杆截面上的自由扭矩和翘曲扭矩与之平衡。即

Tp=Ts+Tw

(2)

在外扭矩增大到一定程度时，在界面的边界处，型钢开始发生屈服，并随着外扭矩的继续增大，屈服面向内扩展，最后全截面形成塑性截面。应用Mises屈服准则可知

(3)

式中，fv为型钢的抗剪强度，fp为型钢的屈服强度。

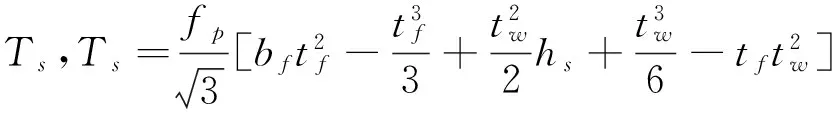
(4)

如图1(d)、(e)，当一端被固定时，扭转受到约束使型钢的上下翼缘产生弯曲变形，翼缘产生剪力，对杆产生翘曲扭矩。

QfL=Mf

(5)

Tw=Qfhs

(6)

当型钢破坏时

(7)

(8)

则型钢承担的极限扭矩

(9)

因此，型钢混凝土构件的极限扭矩计算公式为

(10)

式(2)～(10)各符号的意义见图1。

2 极限扭矩计算公式的试验验证

为了验证计算公式(1～10)的正确性与实用性，选用文献[4]的试验结果进行验证，文献[4]各试件的设计参数见表1，式(10)计算值与试验值的对比见表2。

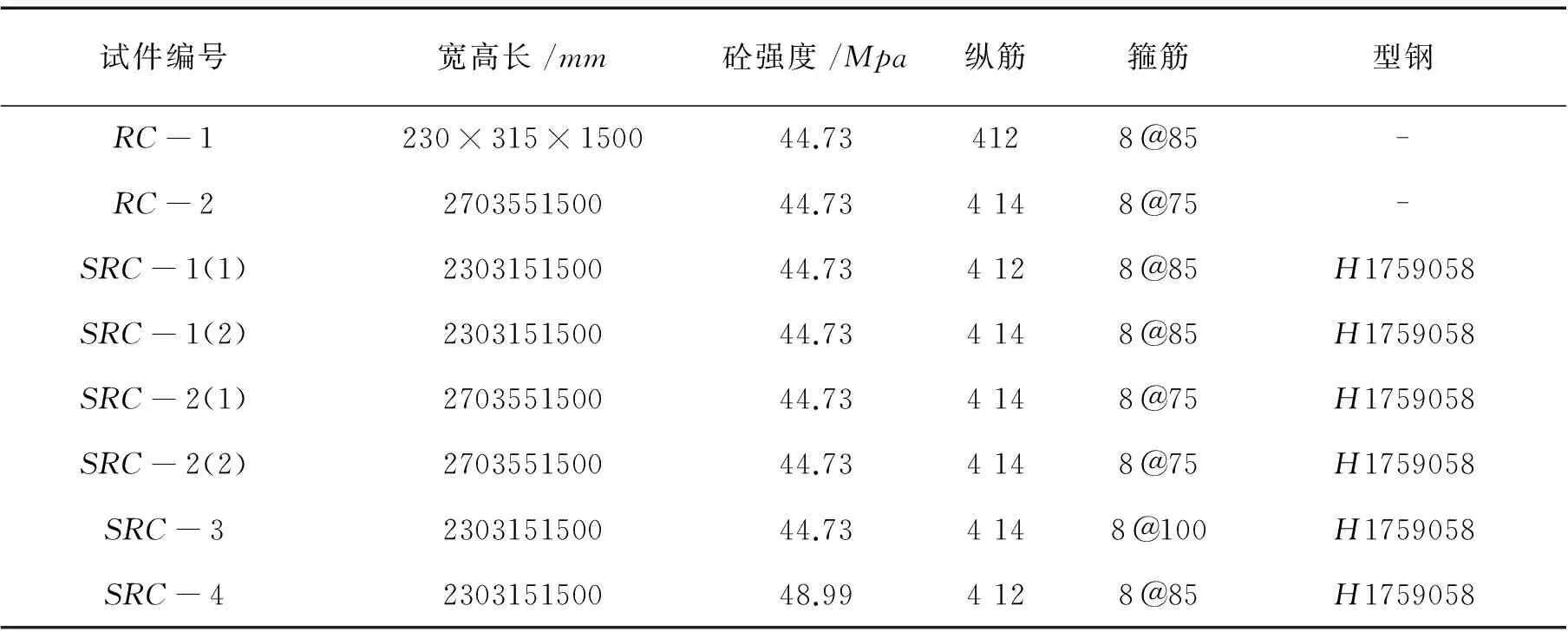
表1 文献[4]试件的设计参数

注：RC-1，RC-2表示钢筋混凝土构件，其余为型钢混凝土构件。表中直径为8、12、14的钢筋的屈服强度分别为328Mpa、406Mpa、411Mpa，型钢的屈服强度为245Mpa。

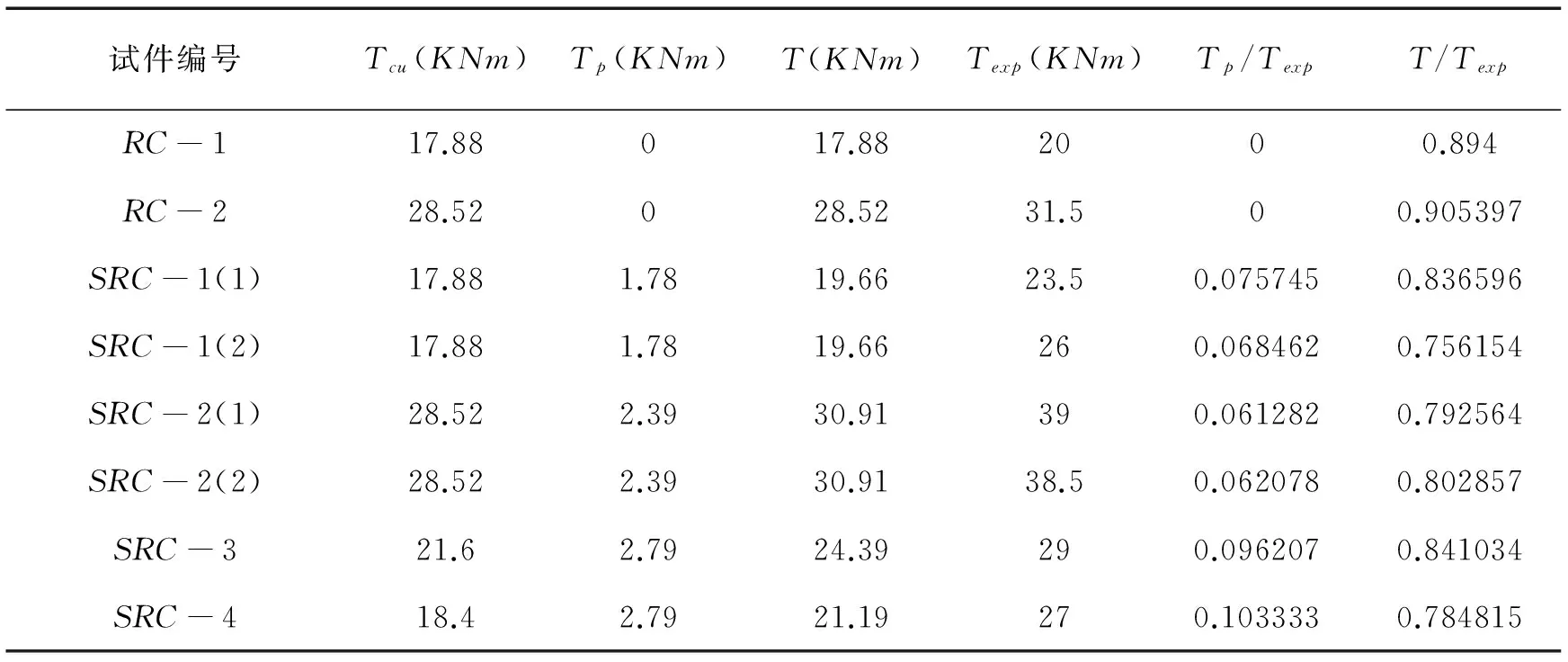
表2 式(1～10)计算值与文献[4]试验值的对比

注：Tcu表示钢筋混凝土的抗扭承载力，Tp表示型钢的抗扭承载力，T表示型钢混凝土的抗扭承载力，Texp表示试验得到的型钢混凝土抗扭承载力。

比较式(10)的计算值与文献[4]试验值发现：计算值与试验值比值的平均值为0.827，变异系数0.053。计算值与试验结果误差较大，其最大误差为24.4%。

3 极限扭矩计算公式的改进优化

分析造成较大误差的原因发现，用式(1)计算的钢筋混凝土抗扭承载能力的计算值与试验值的误差也达到10.6%。这说明公式(1)低估了钢筋混凝土的抗扭承载力。我国钢筋混凝土抗扭强度的计算公式是根据64组有效试验数据回归分析得到的，是半经验半理论公式，取值偏于保守。构件在开裂后，由于纵筋的联系，裂缝的发展受到限制，混凝土骨料之间仍有较大的咬合力。并且加载中，压溃的混凝土受压时存在握裹力，可能造成对于混凝土抗扭作用的低估。此外我国的钢筋混凝土截面核心部分bcor和hcor分别为箍筋内表面范围内截面核心部分的短边和长边尺寸。而HSUT.T.C教授通过计算推导，认为变角空间桁架模型的有效壁厚可以用式(11)简化计算[4-6]，

(11)

式中Tn为扭矩设计值，A为截面面积，fc为混凝土的抗压强度设计值。

这说明截面面积越大、混凝土抗压强度越高，等效壁厚越薄，等效箱型薄壁内的剪力流中心线将外移，抗扭承载力越高。因此，建议，式(1)引入混凝土抗扭强度影响系数γ1和等效箱型有效壁厚变化系数，即：

(12)

式中ucor=(2b+2h-8γ2td),Acor=(b-2γ2td)(h-2γ2td)

则型钢混凝土构件的抗扭承载力公式为：

(13)

为了比较混凝土抗扭强度影响系数γ1和等效箱型有效壁厚变化系数γ2的敏感性，将γ1按步长5%逐级增大，将γ2减按步长5%逐级减小，典型构件RC-2的受扭承载力变化如图2所示。

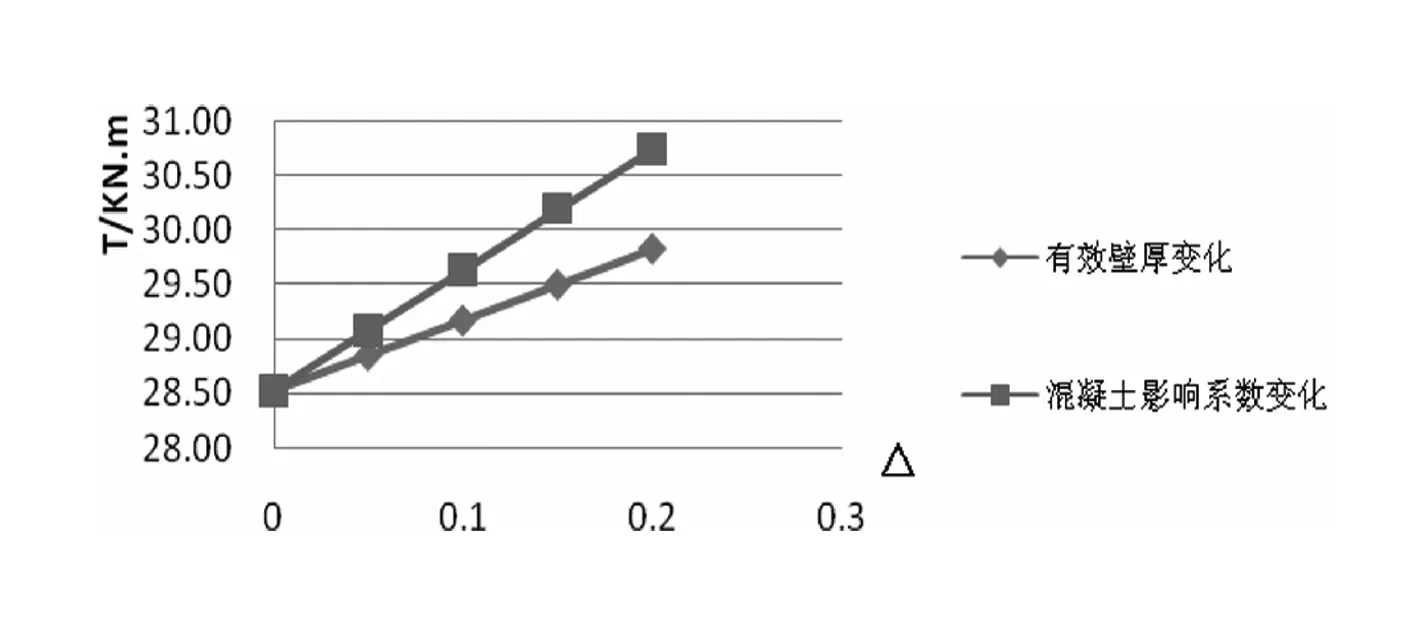
图2 各影响系数变化对承载力的影响

从图2可以看出，γ1对抗扭承载力的影响非常明显。对于型钢混凝土，γ2不仅包含钢筋混凝土间的握裹力及其骨料的咬合力的影响，还包括型钢对于混凝土的约束作用，即组合效应。但由于组合效应与型钢的形状、大小、厚度、位置等有着很大的关系，确定起来非常困难，并且对于处于核心区的开口截面型钢，组合效应发挥不明显，可以将组合效应作为安全储备不加考虑。有效壁厚的变化对钢筋混凝土承载力也有较大影响。我国混凝土规范对于强度较高、截面面积较大钢筋混凝土抗扭承载能力存在低估。对于文献4的试验值，通过回归分析，γ1取1.15，γ2取0.75。 改进后的计算值与试验值的比较见表3。

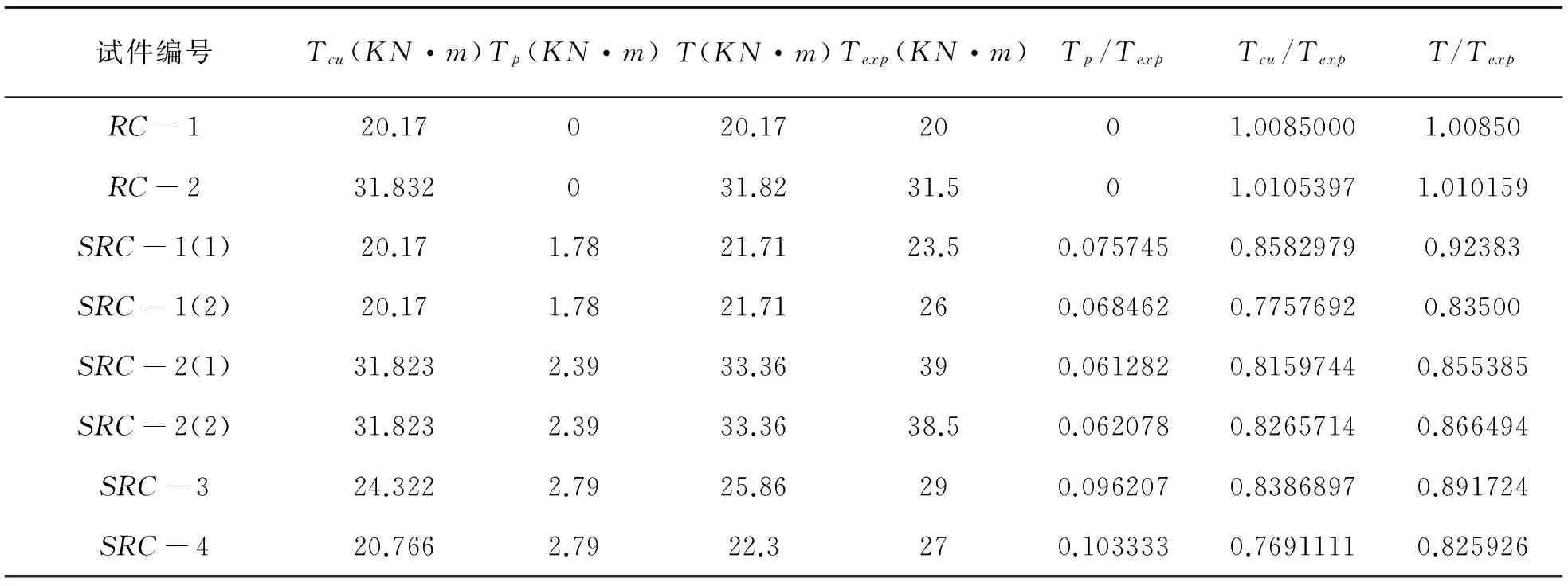
表3 改进后的公式计算值与试验值的对比

注：各符号的具体意义同表2

比较式(13)的计算值与文献[4]的试验值发现，其比值的平均值为0.902，变异系数为0.081，计算值与试验值吻合较好，尤其是钢筋混凝土抗扭承载力计算值与试验值非常接近。式(13)可以符合工程实际应用。分析表3可以发现，型钢的抗扭贡献非常小，即使考虑到组合效应，最大也仅占整个构件抗扭承载力的23.1%左右。这主要是由于文献[4]的H型钢的抗扭刚度非常小，型钢翼缘较窄且处于核心部位，所以对极限承载力影响不明显。

4 型钢截面形式改变对抗扭承载力影响的初步探究

前面的分析可以发现，型钢混凝土的配钢率相比于钢筋混凝土的配钢率有了极大的提高，但是抗扭承载力却提高不多。最主要的原因是开口截面的型钢抗扭刚度太小，且组合效应并不明显。如图3(a)所示，理论上将开口截面变为闭口截面时，型钢内折角增多，受约束的混凝土面积更大，混凝土基本上三向受压，组合效应更加明显。现比较文献[4]中开口截面的型钢与相同截面面积的闭口截面型钢在纯扭作用下的受扭承载力，见图3(b)。

H型钢自由扭转惯性矩、截面最大的剪应力、扭转率分别为：

闭口型钢自由扭转惯性矩、截面最大的剪应力、扭转率分别为：

开口截面型钢与闭口截面型钢两者的比较：

式中Ita、Itb分别为开口截面与闭口截面型钢的由扭转惯性矩，τmaxa、τmaxb分别为开口截面与闭口截面型钢的最大剪应力，θa、θb分别为开口截面与闭口截面型钢的扭率。

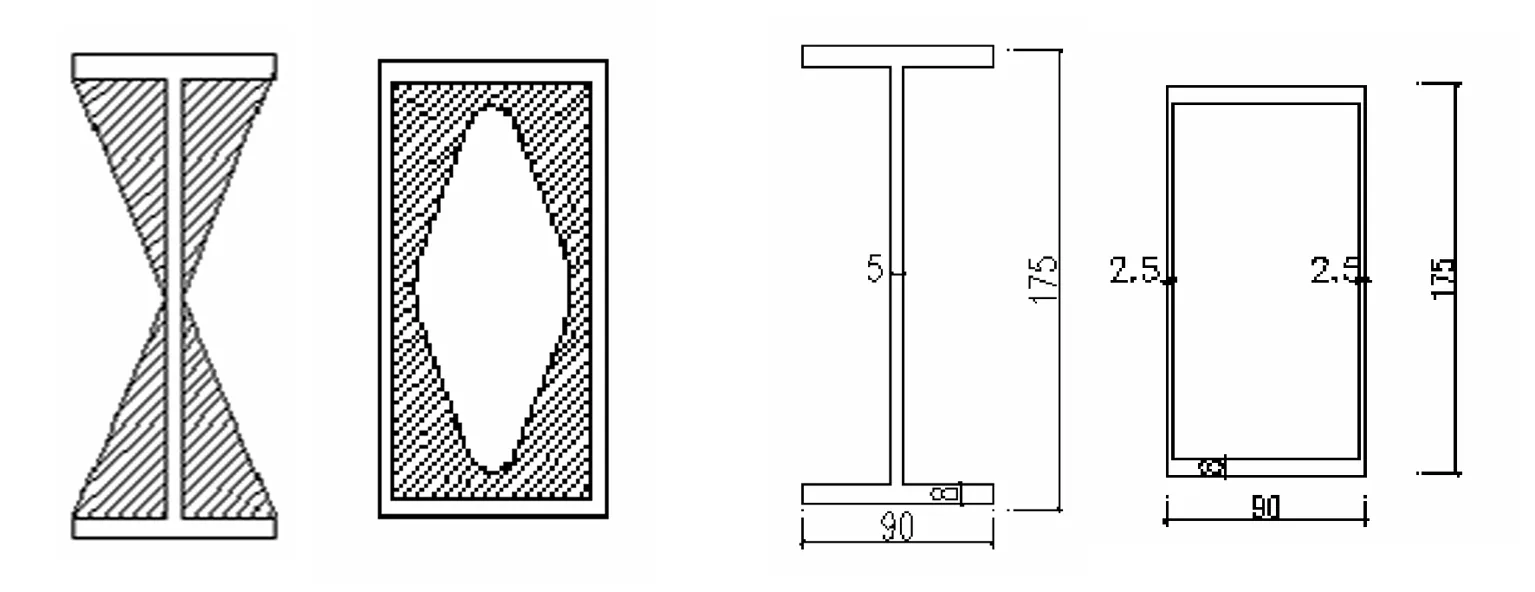
(a)开口截面与闭口截面对混凝土的约束(b)开口截面与闭口截面型钢的尺寸

通过对比可以发现，虽然型钢截面面积完全相同，但是闭口截面的型钢抗扭承载力远比开口截面型钢优越。在抗扭承载力方面，当按最大剪应力控制时，闭口截面约为开口截面的5倍，当按最大变形控制时，闭口截面约为开口截面的152倍。实际上，型钢混凝土一般都是变形过大造成结构破坏。通过型钢截面形式的初步分析，可以发现闭口截面的型钢混凝土具有组合效应明显、抗扭承载力高等优点，工程中应该优先选用闭口截面的型钢。

5 结论

(1)通过叠加法，推导出型钢混凝土构件的纯扭极限承载力计算公式，经过验证能够达到工程应用要求。通过分析发现我国混凝土结构设计规范低估了强度较高、截面面积较大的钢筋混凝土构件的抗扭承载能力。一是对于混凝土的抗扭贡献存在低估，二是等效箱型壁厚的取值过于保守，实际的剪力流中心线外移，承载力提高。本文提出引进增大系数来考虑混凝土的咬合力和握裹力对于抗扭的提高，引进有效壁厚影响系数γ2来表示混凝土抗压强度和截面面积对有效壁厚的影响。对于γ1和γ2的取值需要更多的试验来确定。

(2)通过研究发现H型钢的抗扭承载力比较小，虽然配钢量提高很大，但构件的抗扭承载能力提高极其有限，型钢混凝土的组合效应并不明显。若通过增设H型钢来提高构件的抗扭承载力并不经济。

(3)在抗扭方面，闭口截面型钢比开口截面的型钢具有承载力高，变形小等优势。闭口截面的型钢混凝土组合效应明显，即使应用简单的叠加法，不考虑组合效应，也可以预测闭口截面型钢混凝土构件具有较高的抗扭承载力，具体还有待进一步的试验验证。

[1] 中冶集团建筑研究总院.钢骨混凝土结构设计规程(YB9082-2006)[S].北京：冶金工业出版社，2007.

[2] 中国建筑科学研究院.型钢混凝土组合结构技术规程(JGJ138-2201)[S].北京：中国建筑工业出版社，2001.

[3] 中国建筑科学研究院.混凝土结构设计规范(GB50010-2010)[S].北京：建筑工业出版社，2010.

[4] 王炳晖.纯扭状态下型钢混凝土受扭构件承载力的性能研究[D].桂林：桂林理工大学，2009.

[5] 张根俞.型钢混凝土梁受扭性能的试验研究及理论分析[D].南京:东南大学，2009.

[6] 殷芝霖，张誉，王振东.抗扭[M].北京：中国铁道出版社，1990.

(责任编辑：蒋 华)

Study on Calculation Theory of the Ultimate Pure Torsional Torques of Steel Reinforced Concrete Members

DING Shuang-shuang*, SHAO Yong-jian, SONG Xue-qiang

(College of Civil Engineering, Suzhou University of Science and Technology, Suzhou Jiangsu 215011, China)

Based on the existing calculation formula of the ultimate pure torsional torques of reinforced concretes, the calculation formula of the ultimate torque of the H-type SRC pure torsion members was preliminarily studied, and the calculation equation was put forward by adopting the superposition principle. The comparison between calculation and test results showed that calculated results were in good agreement with the tested data. The torsional performance of the open section steel was also compared with the closed one, and the result manifested that the closed section had a great advantage in resisting torque over the other .

steel reinforced concrete; pure torsional members; ultimate torque calculation

2014-06-10

丁双双(1987-)，男，江苏宿迁人，在读硕士，主要从事钢结构研究；*为通讯作者。

TU37

A

1009-7961(2015)01-0035-06