几种图像去噪算法研究

李 权，赵晋芳

(1.中北大学 信息探测与处理山西省重点实验室，山西 太原 030051；2.内蒙古农业大学，内蒙古 呼和浩特 010018)

几种图像去噪算法研究

李 权1，赵晋芳2

(1.中北大学 信息探测与处理山西省重点实验室，山西 太原 030051；2.内蒙古农业大学，内蒙古 呼和浩特 010018)

图像是一种重要的信息源，通过图像处理可以帮助人们了解信息的内涵.数字图像噪声去除涉及光学系统、微电子技术、计算机科学、数学分析等领域.本文对常用的几种阈值去噪方法进行了分析比较和仿真实现，并且概述了小波阈值去噪的基本原理.最后结合理论分析和实验结果，讨论了一个完整去噪算法中影响去噪性能的各种因素.

小波变换；图像去噪；阈值；MATLAB

0 引 言

近些年来,随着数码产品及各类数字产品的普及，数字图像处理已成为数学技术和计算机技术交叉领域的一个研究热点.图像去噪是数字图像处理中一项基本而又十分关键的技术[1].图像在获取，传输及贮存时总是不可避免地受到各种噪声源的干扰，为了更准确的获取原始信息，图像去噪预处理算法的好坏成为后续处理的关键.随着网络及计算机在人们生活中的日益普及，图像、音频等多种形式的多媒体文件的出现，同时人们对于图像的画质要求也在不断提高，于是图像处理显得越发的重要.

图像空间域去噪方法多.邻域平均法是一种局部空间域处理的算法.图像经过邻域平均法处理后会变得相对模糊，这是因为平均本来就是以图像的模糊为代价来换取噪声的减少的.空间域低通滤波方法也可以平滑图像的噪声，它实际上是通过一个低通卷积模板在图像空间域进行二维卷积来达到去除图像噪声的目的.多幅图像平均法是利用对同一景物的多幅图像取平均来消除噪声的.中值滤波是一种空间域非线性滤波方法，由于它在实际运算过程中并不需要图像的统计特性，所以比较方便.在一定的条件下，它可以克服线性滤波器所带来的图像细节模糊，而且对滤除脉冲干扰及图像噪声最为有效.

图像变换域去噪方法是对图像进行某种变换，将图像从空间域转换到变换域，再对变换域中的变换系数进行处理，再进行反变换将图像从变换域转换到空间域来达到去除图像噪声的目的.将图像从空间转换到变换域的变换方法很多.如傅立叶变换、小波变换[2].每种变换它的变换域得到的系数都有不同的特点，合理地处理变换系数再通过反变换将图像去嗓方法的研究图像还原到空间域可以有效地达到去除噪声的目的[3].

1 传统去噪方法

图1 标准lena图和噪声图

根据噪声产生的来源，大致可以分为外部噪声和内部噪声两大类.这些噪声反映在图像画面上，大致可以分为两种类型的噪声.一类噪声幅值基本相同，但是噪声出现的位置为随机，这种噪声被称为椒盐噪声.一类每一点都存在噪声，但噪声的幅值是随机分布的.从幅值大小的分布统计，这类噪声被称为高斯噪声和瑞利噪声.

1.1 空域滤波

为了从图像中获取更准确的信息，图像去噪预处理算法的好坏成为后续处理的关键.常见的去噪方法有：均值滤波、中值滤波、边界保持类平滑滤波等等.

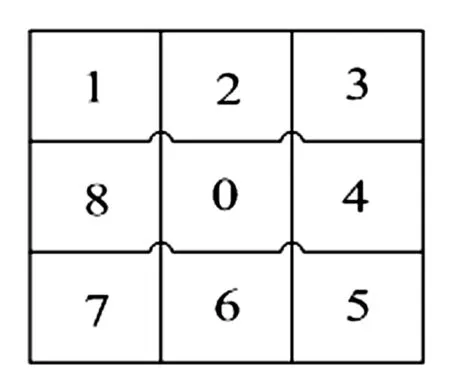
图2 均值滤波示意图

1.1.1 均值滤波

所谓均值滤波实际上就是用均值替代原图像中的各个像素值.如图2所示.

序号为0的是当前像素，序号为1～8的像素是其模板中的近邻像素.求模板中的所有像素的均值，再把该均值赋予当前像素点(x,y),作为处理后图像在该点上的灰度g(x,y),即：

(1)

其中S为模板，M为该模板中包含当前像素在内的像素总个数.考虑到数据分布的平衡性，模板一般选择为3×3、5×5，待处理像素放在模板的中心.

均值滤波对噪声有很好的抑制作用，而且算法简单，但对图像的边缘和细节处的处理方面却不令人满意，虽然噪声抑制效果好，但同时画面的模糊也更加严重.均值滤波对噪声的解决方法是将噪声分布到周围的像素点去.可以看到，在降低噪声的同时，也使得图像变得模糊了.

1.1.2 中值滤波

中值滤波是一种非线性滤波，由于它在实际运算过程中并不需要图像的统计特性，所以比较方便.在一定的条件下，可以克服线性滤波器所带来的图像细节模糊，而且对滤除脉冲干扰及图像扫描噪声最为有效.但是对一些细节多，特别是点、线、尖顶细节多的图像不宜采用中值滤波的方法.

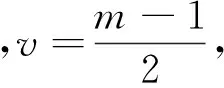
(2)

在实际使用窗口时，窗口的尺寸一般先用3×3再取5×5逐渐增大，直到其滤波效果满意为止.与平均滤波器相比，中值滤波器从总体上来说，能够较好地保留原图像中的跃变部分.

图3 均值滤波去噪效果图 图4 均值滤波去噪效果图

对于椒盐噪声，中值滤波的效果比均值滤波要好得多，但是对模版的选取有一定的要求.如图4所示，随着模版的变大，模版内数值幅值范围相对的变小，所以图像的清晰度在一定程度上遭到了破坏.

基于空域的平均滤波法和非线性的中值滤波都是通过对图像像素的灰度值进行运算，达到平滑图像的效果.平均滤波是以点邻域像素灰度平均值来代替该点的灰度值，而中值滤波则以点邻域像素灰度值中值来代替该点的灰度值，因此，对于随机噪音的抑制能力，中值滤波器的性能要比均值滤波器的差些.但对于脉冲干扰来讲，特别是脉冲宽度小于滤波器的窗口宽度一半，中值滤波还是很有效的.不过，他们在平滑图像的同时亦会使图像轮廓变得模糊，它们的噪音平滑效果与窗口的宽度有关，窗口宽度越宽，噪音平滑效果越好，但图像就越模糊，这个矛盾难于解决，也是均值滤波和中值滤波的缺点.

1.2 频域低通滤波

在分析图像信号的频率特性时，一幅图像的边缘，跳跃部分以及颗粒声代表图像信号的高频分量，而大面积的背景区则代表图像信号的低频分量.用滤波的方法滤除其高频部分就能去掉噪声使图像得到平滑，由卷积定理可知:

G(u,v)=H(u,v)F(u,v)

(3)

式中，F(u,v)是含噪声图像的傅里叶变换，G(u,v)是平滑后图像的傅里叶变换，H(u,v)是低通滤波器传递函数.利用H(u,v)使F(u,v)的高频分量得到衰减，得到G(u,v)后再经过反变换就得到所希望的图像g(x,y)了.低通滤波平滑图像的系统框图5所示.

图5 频域空间滤波图

下面介绍几种常用的低通滤波器.

(1)理想低通滤波器(LIPF)

一个理想的低通滤波器的传递函数由下式表示:

(4)

式中D0是一个规定的非负的量，称为理想低通滤波器的截止频率.D(u,v)代表从频率平面的原点到(u,v)点的距离，即:

(5)

图6 理想低通滤波去噪效果图

理想低通滤波器平滑处理的概念是清楚的，但它在处理过程中会产生较严重的模糊和振铃现象，使其平滑效果下降.

(2)巴特沃思低通滤波器(BLPF)

巴特沃思低通滤波器与ILPF不同，它的通带与阻带之间没有明显的不连续性，因此它的空域响应没有“振铃”现象发生，模糊程度减少.一个n阶巴特沃思低通滤波器的传递函数为:

(6)

图7 理想低通滤波去噪效果图

与理想低通相比，它保留有较多的高频分量，所以对噪声的平滑效果不如理想低通滤波器.

除了上述滤波方法外，学者们还提出了其它的基于频域滤波的图像去噪方法，如Wiener滤波等.各种低通滤波器的性能比较如表1所示:

表1 各种低通滤波器的性能比较

上述经典去噪方法要么完全在频率域，要么完全在空间域展开.这两类消噪方法造成了顾此失彼的局面，虽然抑制了噪声，却损失了图像边缘细节信息，造成图像模糊.因此，提出了基于小波变换的去噪方法研究.小波分析由于在时域频域同时具有良好的局部化性质和多分辨率分析的特点，能有效地把信号和噪声区别开来，因此不仅能满足各种去噪要求如低通、高通、陷波、随机噪音的去除等，而且与传统的去噪方法相比较，有着无可比拟的优点，成为信号分析的一个强有力的工具，被誉为分析信号的数学显微镜.

2 小波变换的图像去噪

2.1 小波变换

在实际应用中，常常有些非平稳信号，如音乐、语音信号等它们的频域特性都随着时间的变化而改变，这时傅立叶变换明显表现出了其中的不足.1986年，由Y.Meyer发现了构成希尔伯特空间的规范正交基，从而证明了小波正交系的存在.1987年，Mallat将计算机视觉领域内的多尺度分析的思想引入小波分析中，提出了多分辨率分析的概念，并提出了相应的分解和重构快速算法—Mallat算法，从而统一了以前所有具体正交小波基的构造[4-5].

2.2 小波去噪问题的描述

在数学上，小波去噪问题的本质是一个函数逼近问题.即如何在由小波母函数伸缩和平移版本所展成的函数空间中，根据提出的衡量准则寻找对原信号的最佳逼近以完成原信号和噪声信号的区分.这个问题可以表述为：

由此可见小波去噪方法也就是寻找从实际信号空间到小波函数空间的最佳映射.尽管在很大程度上小波去噪可以看成是低通滤波,但是由于在去噪后还能成功地保留图象特征，所以在这一点上又优于传统的低通滤波器.由此可见小波去噪实际上是特征提取和低通滤波功能的综合.其流程框图如图8所示.

图8 小波去噪流程框图

2.3 小波变换的图像去噪原理

二维塔式快速小波变换的分解过程如图9所示[6]，重构过程如图10所示.

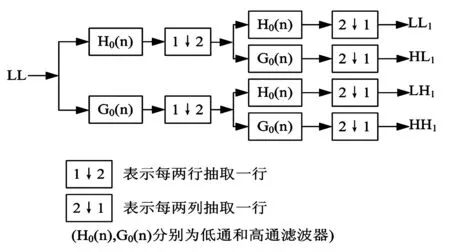
图9 二维小波分解示意图

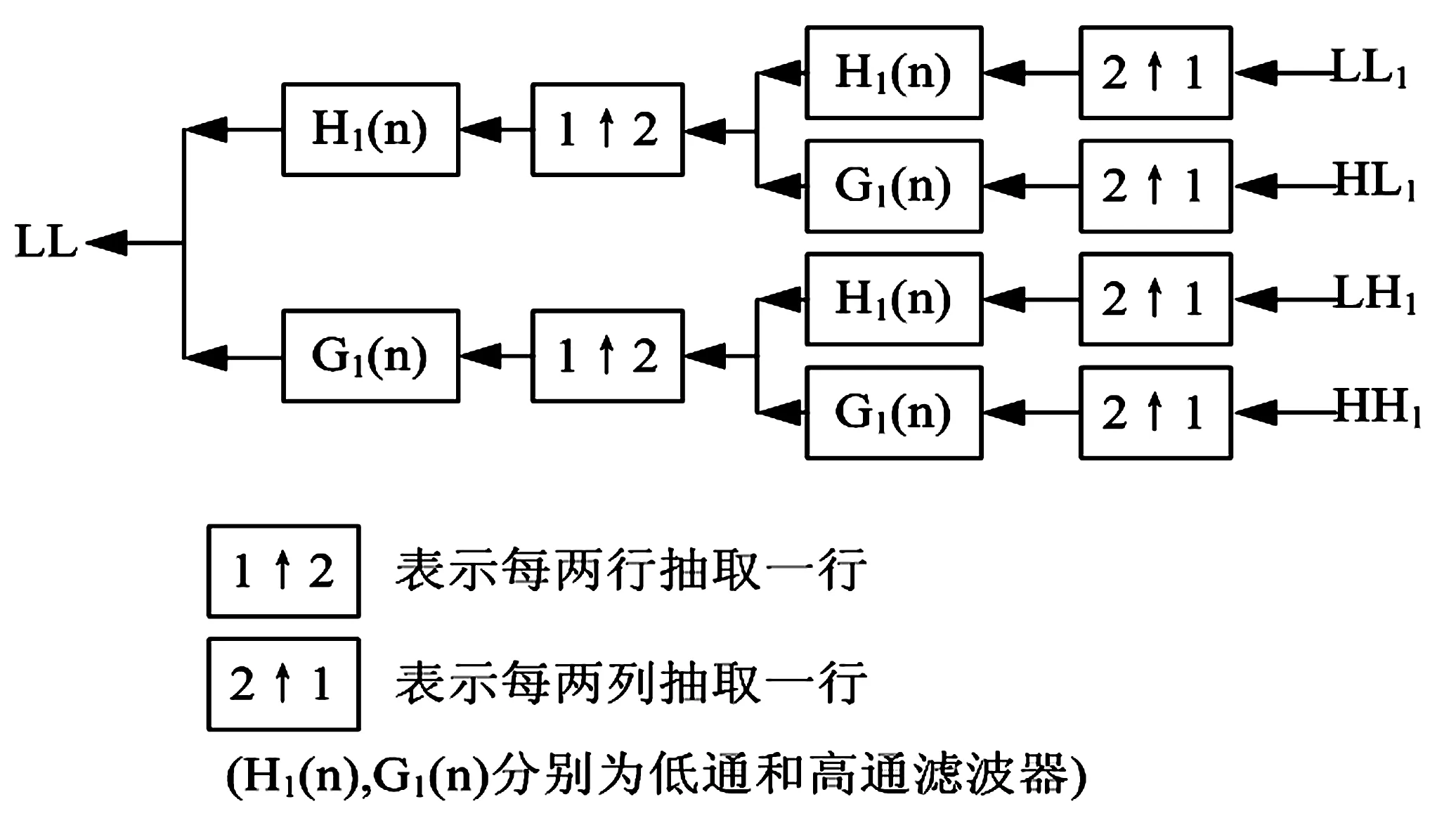
图10 二维小波重构示意图

2.4 阈值的选取

(7)

其中j是小波分解尺度.

2.5 波去噪的实现

图11 小波去高斯噪声效果图 图12 小波去椒盐噪声效果图

在阈值选择上也可以使用统一的全局阈值.虽然有关小波变换的函数是在小波工具箱中提供的，但在图像处理中利用小波变换去除图像中的噪声却是一种有效的方法，利用小波函数去除图像中的噪声过程如下：

(1)利用求去噪缺省值函数ddencmp求去噪声的缺省值.

(2)利用小波函数wdencmp对图像去噪，可以使用全局阈值.

图13 wpbmpen进行全局阀值去噪效果图

对于阈值函数的确定，Donoho提出了两种：硬阈值和软阈值.在硬阈值处理中，由于收缩函数的不连续性，会在恢复的信号中产生一些人为的“噪声点”.软阈值的连续性较好.

图14 全局阀值和SURE最优基进行降噪效果图

从含噪图像可以看出噪声含量非常强，而从去噪的结果可以看出，通过小波去噪后的图像基本和原图像一致.

3 几种算法的比较

均值滤波对噪声的解决方法是将噪声分布到周围的像素点去.如同将一把盐撒到水中，虽然咸味变淡了，可是盐的总量并不会少.使用均值滤波对图像去噪时，在降低噪声的同时也会使得图像产生模糊；中值滤波的算法较均值滤波虽较为复杂，但对噪声的抑制效果却是要好很多.但对模版的大小选取很是重要，模版太大也会使得图像的清晰度遭到破坏；小波去噪更多考虑的是在保留信号主要特征的基础上，如何滤除噪声，就是从含噪图像中恢复原始图像的同时保持原始图像的特征.不仅保持原图像的空间特性，而且很好的提取了图像的高频信息.在低频处有很好的频率特性，在高频处有很好的空间选择性.

[1] (美)冈萨雷斯(Rafael Gonzalez)，伍兹(Richard E.Woods),艾丁斯(Steven L.Eddins).数字图像处理 MATLAB版[M].北京：电子工业出版社, 2005.

[2] 飞思科技产品研发中心.小波分析理论与MATLAB 7实现[M]. 北京：电子工业出版社, 2005.

[3] 杨杰. 数字图像处理及MATLAB实现[M]. 北京：电子工业出版社, 2007.

[4] 董长虹,高志,余啸海. Matlab小波分析工具箱原理与应用[M]. 北京：国防工业出版社, 2004.1.

[5] 陈武凡. 小波分析及其在图像处理中的应用[M]. 北京：科学出版社, 2004.

[6] 李建平. 小波分析与信号处理—理论、应用及软件实现[M].重庆：重庆出版社, 1997.

【责任编辑：王军】

Several kinds algorithms of image denoising

LI Quan1，ZHAO Jinfang2

(1.Shanxi Key Laboratory of Signal Capturing & Processing, North University of China, Taiyuan 030051,China;2.Inner Mongolia Agricultural University, Hohhot 010018,China)

Image is an important source of information, it can help people understand the connotation of the information through image processing. Digital image noise denoising involve in optical systems, microelectronics technology, computer science, mathematical analysis, etc. In this paper, the commonly used several threshold denoising methods has carried on the comparative analysis and simulation, and summarizes the basic principle of wavelet threshold denoising. Finally combined with theoretical analysis and experimental results, a complete denoising is discussed various factors influencing the performances of denoising algorithm.

wavelet transform; image denoising;the threshold value; matlab

2014-05-29

国家自然科学基金资助项目(2012021011-2);山西省高等学校优秀创新团队支持计划资助

李权(1987-)，男，山西山阴县人，中北大学硕士研究生，主要从事CT重建的研究.

Q969.26

A

1672-3600(2015)03-0027-06