具有时变参数的分数布朗运动环境下欧式缺口期权定价
2015-03-03白婷李翠香
白婷,李翠香
(河北师范大学 数学与信息科学学院,河北 石家庄 050024)
具有时变参数的分数布朗运动环境下欧式缺口期权定价
白婷,李翠香
(河北师范大学 数学与信息科学学院,河北 石家庄 050024)
经典的期权定价模型假设股票价格服从标准几何布朗运动,但金融实证表明用分数布朗运动描述股票价格过程更贴近市场.本文假设标的资产服从几何分数布朗运动,且无风险利率r(t),红利率q(t),波动率σ(t)均为随时间变化的确定函数,运用拟鞅方法求出了欧式缺口期权的定价公式,推广了相关结果.
分数布朗运动;拟鞅;时变参数;欧式缺口期权
0 引 言
传统的期权定价假设股票的价格服从几何布朗运动,而金融实证表明股票市场价格具有长期依赖性和自相似性,用分数布朗运动来代替几何布朗运动更贴近市场.
Hurst参数为H∈(0,1)的分数布朗运动是一个高斯过程且满足:
(1)BH(0)=E[BH(t)]=0,(t≥0),
欧式缺口期权是一种奇异期权,其到期收益不是与执行价格K比较,而是与另外一个常数G(G为缺口)比较.在T时刻欧式缺口看涨期权的收益为
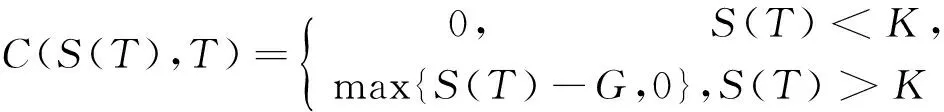
(1)
在T时刻欧式缺口看跌期权的收益为

(2)
由(1)(2)可以看出,当K=G时,缺口期权即为标准欧式期权.
张艳,周圣武,等[3]利用偏微分方程的方法给出了随机利率模型下标的资产服从标准几何布朗运动时欧式缺口看涨和看跌期权的定价.何成洁,沈明轩[4]研究了标的资产服从几何分数布朗运动,无风险利率r,红利率q,波动率σ均为常数时欧式缺口看涨和看跌期权的定价.蔺捷,薛红等[5]利用保险精算的方法研究了当标的资产服从几何分数布朗运动,无风险利率r服从Vasicek模型,波动率σ为常数时欧式缺口期权的定价公式.本文假设标的资产服从几何分数布朗运动,无风险利率r(t),红利率q(t),波动率σ(t)均为时间的函数,应用随机微分理论和拟鞅方法得到欧式缺口看涨和看跌期权的定价公式.
1 预备知识
以下假设市场满足B-S模型的条件,即市场是均衡的完备的且无套利存在,并假设在市场中仅有两种投资证券:无风险资产即债券和股票,其中债券价格M(t)满足:
dM(t)=r(t)M(t)dt,
股票价格S(t)满足:
dS(t)=[r(t)-q(t)]S(t)dt+σ(t)S(t)dBH(t),
(3)
其中r(t)为无风险利率,q(t)为红利率,σ(t)为瞬时波动率.
满足(3)的解为
(4)
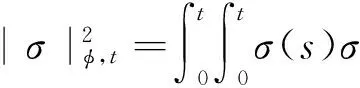
引理1[2](1)BH(t)是拟鞅;
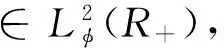
(5)
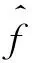

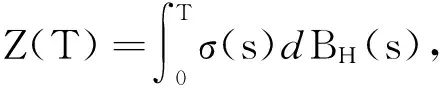
其中
因为两个函数卷积的傅立叶变换等于这两个函数傅立叶变换的乘积,所以
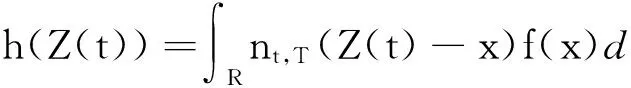
引理2得证.

证明:由于市场是完备的,所以存在自融资组合(m(t),s(t)),使得
F(t)=mt(t)M(t)+s(t)S(t),F(T)=F,
且有
dF(t)=m(t)dM(t)+s(t)dS(t)+q(t)s(t)S(t)dt=r(t)F(t)dt+σS(t)s(t)S(t)dBH(t).
从而

两边积分并整理得

因为F(T)=F,且由引理3知
所以
从而引理3得证.
2 欧式缺口期权的定价
定理1 到期日为T,执行价格为K,缺口为G的欧式缺口看涨期权在期满前任意时刻t的价值为
其中
证明:由引理3及(1)式知

由(4)式知
(6)
所以由引理2得
(7)
另外由(4)式可知
(8)
由(6)式和(8)式得
(9)
由(7)式和(9)式,定理1得证.
定理2 到期日为T,执行价格为K,缺口为G的欧式缺口看跌期权在期满前任意时刻t的价值为
其中d1,d2在定理1中已定义.
定理2的证明类似于定理1的证明,在此省略.
[1] HU Y, OKSENDAL B. Fractional white noise calculus and application to finance[J]. Inf. Dim. Anal. Quantum Prob. Rel. Top, 2003, 6(1):1-32.
[2] NECULA C. Option pricing in fractional Brownian motion environment[R]. Preprint, Academy of Economic Studies Bucharest, www.dofin.ase.ro/.
[3] 张艳,周圣武,韩苗,等.随机利率Vasicek模型下的欧式缺口期权的定价研究[J].大学数学,2012, 28(4):98-101.
[4] 何成洁,沈明轩.分数布朗运动环境中欧式缺口期权的定价[J].高校理论研究,2008, 24:435-439.
[5] 蔺捷,薛红,王晓东.分数布朗运动环境下缺口期权定价[J].哈尔滨商业大学学报,2012(05):616-619.
【责任编辑:王军】
Pricing of European gap options under fractional Brownian motion with time-varying parameters
BAI Ting, LI Cuixiang
(College of Mathematics and Information Science, Hebei Normal University, Shijiazhuang 050024,China)
In the classical option pricing model stock price was supposed to follow standard geometric Brownian motion. However financial evidence shows that using fractional Brownian motion to describe the process of stock price is more closer to the market. In this paper, we assume that underlying asset price follows geometric fractional Brownian motion, the riskless interest rater(t), dividend rateq(t), and the volatilityq(t) of the stock are all time-varying certain functions. Using quasi-martingale method, we get the pricing formulas of European gap option. The results extend the related results.
fractional Brownian motion; quasi-martingale; time-varying parameters; European gap options
2014-07-08
国家自然科学基金资助项目(10771049);河北省自然科学基金资助项目(A2012205028)
白婷(1989-),女,河北新乐人,河北师范大学硕士研究生,主要从事金融数学的研究.
O211.6
A
1672-3600(2015)03-0019-03
