自旋相干态法研究自旋轨道耦合BEC系统的基态性质
2015-03-03赵佳
赵 佳
(太原工业学院 理学系,山西 太原 030008)
自旋相干态法研究自旋轨道耦合BEC系统的基态性质
赵 佳
(太原工业学院 理学系,山西 太原 030008)
文章采用自旋相干态的方法研究自旋轨道耦合玻色爱因斯坦凝聚(BEC)系统的基态性质,在自旋相干态表象下把系统的哈密顿量对角化, 由变分法求出系统的基态能谱、原子布居数和光子数,从而得到系统的量子相变,与Holstein-Primakoff方法所得的结果一致.
自旋相干态;自旋轨道耦合;能谱;原子布居数;光子数
0 引言
自旋轨道耦合(SOC)描述了粒子的自旋和轨道自由度之间的相互作用.在凝聚态物理中,电子的自旋轨道耦合不仅产生了一些重要的量子现象,例如自旋和反常霍尔效应、拓朴绝缘体和拓朴超导等,在实现自旋电子学和拓扑量子计算方面也发挥了重要的作用[1].本文用自旋相干态方法研究自旋轨道耦合玻色爱因斯坦凝聚(BECs)系统的基态性质,主要思路:首先由玻色子算符取平均场近似后,得出等效赝自旋哈密顿算符,然后应用自旋相干态变换将其对角化[2],最后将能量泛函对复参数求变分并取极小值,从而得出基态能量和原子布居数的精确解.
1 模型及哈密顿量

图1 自旋轨道耦合实验装置示意图

(1)
(2)
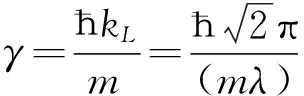
(3)
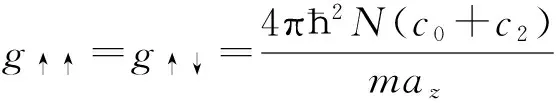
既然s波散射长度在实验可以测量:c0=100.86aB和c2=-0.46aB[3],其中aB是玻尔半径,那么可以得到g↑↑=g↑↓≈g↓↓,这说明囚禁BEC表现出原子间碰撞的强相互作用,而在这种强相互作用下,所有超冷原子都被限制在相同的基态上,每个原子的动量都完全一样.引入两个玻色算符
(4)
通过计算可以得到自旋轨道耦合驱动BEC系统的有效哈密顿量[4]
(5)
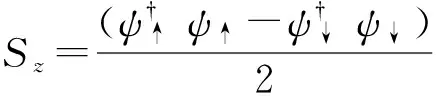
在图1所示的系统中,玻色子模在y方向上与超冷原子间没有相互作用,所以该系统的性质可以用下面的单模Dicke模型哈密顿量来描述[5]
(6)

2 理论方法
在玻色场相干态表象中,计算方程(6)所对应哈密顿算符的期待值
(7)
其中复数α=u+iυ是玻色子湮灭算符a的本征值,有a|α〉=α|α〉.
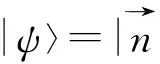
(8)
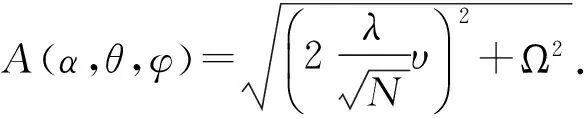
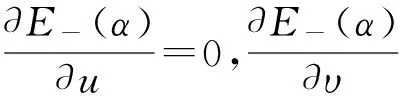

那么,基态能谱
(9)
在热力学极限(N→∞)下,HP方法给出了同样的结果[9,10],而自旋相干态法对任意原子数都成立.从图2可以看出,基态能量一阶导在临界点附近连续
在北极规范下,激发的宏观量子态能谱
(10)
原子布居数
(11)
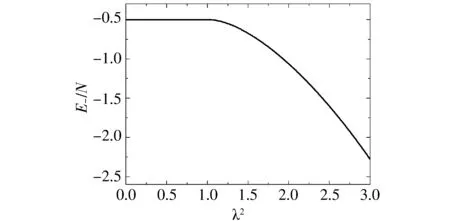
图2 基态能谱随耦合参数λ2的变化曲线
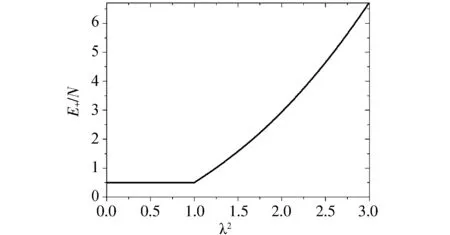
图3 宏观量子态能谱随耦合参数λ2的变化曲线

图4 原子布居数随耦合参数λ2的变化曲线

图5 光子数随耦合参数λ2的变化曲线
3 结果与讨论
参数ω=Ω=1,则有相变临界点λc=1.当λ<λc时,系统处于正常相;当λ>λc时,系统处于超辐射相.随着耦合参数λ2的增大,系统从正常相变化到超辐射相,发生了量子相变.基态能谱在相变临界点处的突然变化说明系统发生了量子相变,原子布居数和光子数在相变临界点处从零开始急剧增加.
[1] LIAN Jinling,YU Lixian,LIANG J Q.Orbit-induced spin squeezing in a spin-orbit coupled Bose-Einstein condensate[J].Sci Rep,2013,3(1):3166-3166
[2] LAI Y Z,LIANG J Q.Time-dependent quantum systems and the invariant Hermitian operator[J].Phys Rev A,1996,53:3691-3693
[3] LIN Y J,GARCIA K J,SPIELMAN I B.Spin-orbit-coupled bose-einstein condensates[J].Nature,2011,471:83-86
[4] ZHANG Y,CHEN G, ZHANG C.Tunable spin-orbit coupling and quantumphase transition in a trapped Bose-Einstein condensate[J].Sci Rep,2013,3(1):1937-1937
[5] DICKE R H.Coherence in spontaneous radiation processes[J].Phys.Rev,1954,93:99-110
[6] LIAN Jinling,ZHANG Yuanwei,LIANG Jiuqing.Macroscopic quantum states and quantum phase transition in the dicke model[J].Chin Phys Lett,2012,29(1):060302-060302
[7] EMARY Clive, BRANDES Tobias.Quantum chaos triggered by precursors of a quantum phase transition: The Dicke model[J].Phys Rev Lett,2003,90:044101-044104
[8] EMARY Clive, BRANDES Tobias.Chaos and the quantum phase transition in the Dicke model[J].Phys Rev E,2003,67(1):066203-066203
[9] CASTAFLOS O,ACHAR E N, HIRSCH J G.No singularities in observables at the phase transition in the Dicke model[J].Phys Rev A,2011,83(1):05160-05160
[10] EMARY Clive, BRANDES Tobias.Phase transitions in generalized spin-boson (Dicke)models[J].Phys Rev A,2004,69(1):053804-053804
Studying the Ground-State Properties of the Spin-Orbit-Coupled BEC by Means of the Spin Coherent-State Transformation
ZHAO Jia
(Department of Science, Taiyuan Institute of Technology, Taiyuan 030008, China)
We study the ground-state characteristics of the spin-orbit-coupled BEC by means of the spin coherent-state transformation. In the picture of the spin coherent-state,the Hamiltonian of the spin-Orbit-coupled BEC can be diagonalized by the spin coherent-state transformation. Based on the variational method we are able to obtain the expression of the ground-state energy spectra, the atomic population and the photon number. Consequently, The quantum phase transition is detected by these physical quantities. the same results are exactly obtained by using the Holstein-Primakoff approach.
the spin-orbit-coupled; the spin coherent state transformation; the energy spectra;the atomic population;photon
2015-10-11
赵 佳(1983-),女,山西太原人,太原工业学院理学系助教,主要从事量子理论研究.
1672-2027(2015)04-0004-04
O175
A
