基于最小支撑树的光纤布线——以福建师范大学福清分校为例

谢超凡，徐鲁雄

(福建师范大学 福清分校,福建 福清 350300)

基于最小支撑树的光纤布线
——以福建师范大学福清分校为例

谢超凡，徐鲁雄

(福建师范大学 福清分校,福建 福清 350300)

信息技术的迅猛发展,人们对数据的通信要求的质量也越来越高,为了全校师生员工的科研、教学和信息检索提供了更好的网络服务.文章使用最小支撑树来解决校园网光纤布线,在提高学校网络服务效率的同时减少费用的支出,达到效率和成本兼顾．

最小支撑树;光纤;校园网

计算机网络使用人员不仅仅追求高质量的办公效率,对于图像、音频、视频等多媒体数据传输的速度等与生活娱乐相关的信息也提出更高的要求[1-2]．校园网作为学校网络的信息承载中心,其带宽和传输速率直接影响到全校师生对信息系统的使用效率和满意度．基于计算机和网络技术建立起来的对教学、科研、管理、技术服务、生活服务等校园信息的收集、处理、整合、存储、传输和应用,使数字资源得到充分优化利用的一种虚拟教育环境．数字化校园用层次化、整体的观点来实施校园信息化建设,将校园网上信息进行更好的组织和分类,让用户在网上快速发现自己需求的信息．为师生提供网上信息交流环境,让管理人员科学地、规范地管理自己的数据,并将这些信息方便地发布出去．

在信息化浪潮席卷全球、日益渗透到社会生活各个领域的今天,数字化校园建设如火如荼．特别是欧美、日本等发达国家高度重视信息化建设,早在20世纪90年代初几乎所有的高校便建成了比较完善的校园网,各个职能部门都基本实现了网络化、信息化管理．我国高校信息化建设起步较晚,近十年来,随着我国高等教育的快速发展,高校办学规模不断扩大,使各个管理部门任务越来越繁重,不仅增加了工作量,更增大了工作难度,管理手段落后将直接影响教学质量和办学水平．教育信息化已成为教育改革与发展的必然要求和重要推动力．

通过建设一个高速、安全、可靠、可扩充的网络系统,实现校内信息的高度共享、传递,教学及管理信息化,并通过与广域网的互联,实现校际间的信息共享及与INTERNET的连接,实现远程教育,为学校的教学、管理、日常办公、内外交流等各方面提供全面、切实的支持．

由于上述的需求对校园网建设提出了很高的要求,归根结底校园网建设的基础都是实现校内网络传输全光纤化．然而,网络的建设不是一劳永逸的,随着招生规模的扩大和师资队伍的不断壮大,对校园网网络要求只会越来越高,在这种环境下,需要提高学校的光纤覆盖和光纤升级改造,但是在改造过程中不能仅仅只考虑到设备的先进性和成熟性,对于经济性和实用性同样重要．本文使用最小支撑树来保证网络节点正常高速通信的同时,达到成本最小[3-4]．

1 校园网网络拓扑构造

节点的集合代表各个要铺设的楼与中心机房记为V,如果要在两个楼或者与中心机房铺设光纤则用边进行连接,所有边的集合记为E,由于铺设的光纤成本依赖于光纤的长度,则边的权重直接用两个节点之间的距离来表示记为W.为了保证学校的行政办公,因此行政楼与机房只能直连,其他楼之间由于地理位置和高度的原因确实存在铺设的难题则距离就用+∞表示,可得网络拓扑图，见图1.

两个节点之间无法铺设或者存在铺设障碍的将权重定义为+∞,不在图上画出,现在要解决的问题是要确定铺设哪些光纤,以使每两个节点之间通信的总成本最低．实际上,这就是最小支撑树的问题．首先,将边的权重按从小到大排列如表1.

表1 各楼层权重分布 单位:m

2 最小支撑树构造

构造最小支撑树常用的方法有避圈法和破圈法构造,本文详细使用避圈法构造成本最低的光纤铺设,用破圈法验证一下．

2.1 使用避圈法构造(kruskal)

开始选一条最小的边,以后每一步中,总从与已选边不构成圈的那些未选边中,选一条权最小的(每一步中,如果有两条或两条以上的边都是权最小的边,则从中任选一条)．

算法的具体步骤如下:

第1步:令i=1,E0=Ø

第2步:选一条边ei∈EEi-1,使ei是使(V,Ei-1∪{ei})不含圈的所有边e(e∈EEi-1)中权最小的边．令E=Ei-1∪{ei},如果这样的边不存在,则最小支撑树T就构造好了．

第3步:把i换成i+1,转第2步．

按照算法构造的最小支撑树如下:

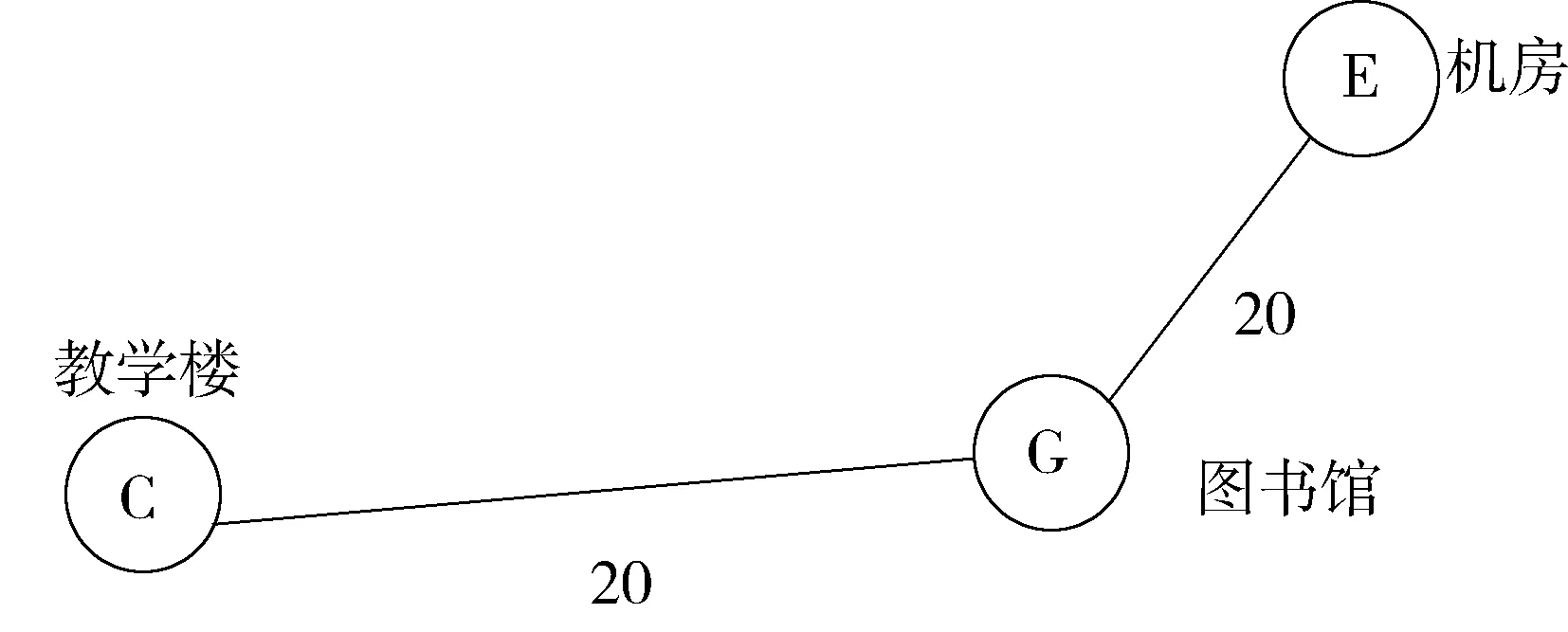
仿造上述的步骤可得到如下的构造图,见图2.

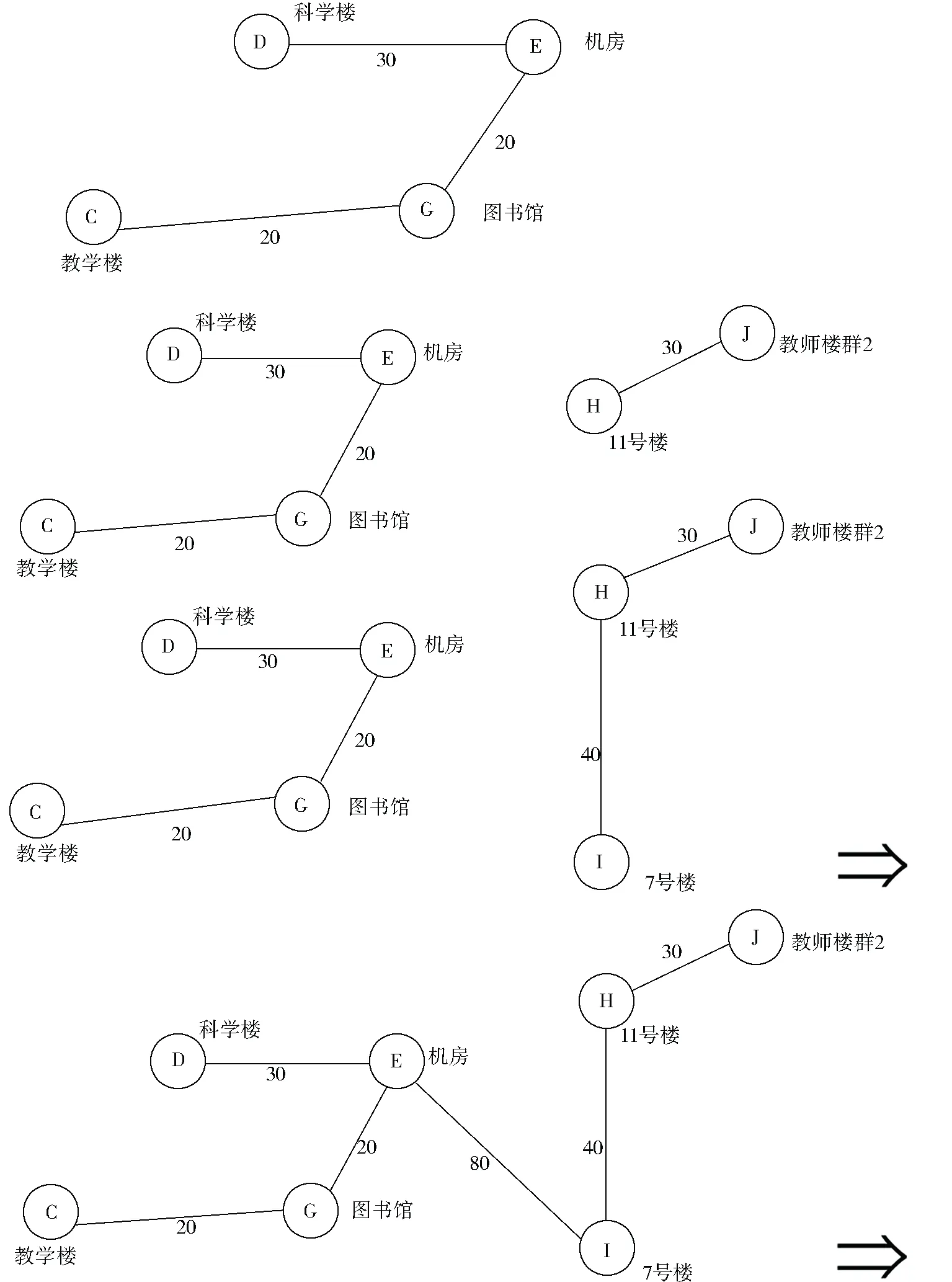
图2 最小支撑树T

2.2 使用破圈法构造(Rosenstiehl和管梅谷)

任取一个圈,从圈中去掉一条权最大的边(如果有两条或两条以上的边都是权最大的边,则任意去掉其中一条)．在余下的图中,重复这个步骤,直至得到一个不含圈的图为止,这时的图便是最小树．

算法具体步骤:

第1步:i=1,V0=V．

第2步:若Vk中不含圈,转3.否则,设C为Vk中一个圈,ek为C上带权最大的边,令Vk+1=Vk-ek;k=k+1,重复2．

第3步:结束．

由图3可知利用破圈法构造的最小支撑树与避圈一致．

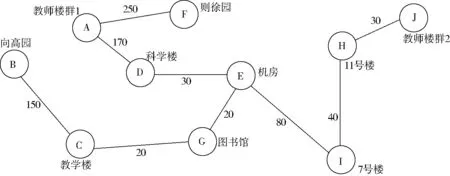
图3 最小支撑树T

3 结论

本文首先利用图来对校园网的网络建立拓扑结构,将成本看成是使用光纤的总长度,问题转化为在保证网络节点正常通信的同时,怎么使得铺设光纤使得总成本达到最小,由此自然而然借用图论中的最小支撑树理论,从而求出最优的方案,为校园网建设的科学决策提供理论和实际的依据．

[1] 姚 坤.高校校园网建设方案的设计与研究[D].银川：北方民族大学,2013

[2] 邓宝林.高校校园网改造工程的规划与设计[D].大连：大连理工大学,2013

[3] 杨文宇.基于最小生成树算法的配电网架优化规划[D].西安：西安理工大学,2005

[4] 沈 广，陈允平，刘 栋.基于最小生成树编码的配电网恢复遗传算法[J].电力系统自动化,2007(14)：31-33

Based on the Minimum Spanning Tree of Fiber Optic Cabling ——Case Study of Fuqing Branch of Fujian Normal University

XIE Chaofan, XU Luxiong

(Fuqing Branch of Fujian Normal University, Fuqing 350300, China)

The rapid development of information technology, people's requirements are also increasingly for quality of data,providing a better network services for school staff and students’ research, teaching and information retrieval. This article uses the minimum spanning tree to solve the campus fiber optic cabling, network services to improving school efficiency of network services while reducing the cost of spending to achieve both efficiency and cost.

spanning tree; fiber; campus network

2015-10-24

谢超凡(1984-),男,硕士,福建师范大学福清分校实验师,主要从事数据挖掘研究.

1672-2027(2015)04-0034-05

TP202

A