巴拿赫空间中一类非线性二阶微分方程组的边值问题
2015-03-03周碧波张润玲
周碧波,张润玲
(吕梁学院 数学系,山西 吕梁 033000)
巴拿赫空间中一类非线性二阶微分方程组的边值问题
周碧波,张润玲
(吕梁学院 数学系,山西 吕梁 033000)
利用空间中锥理论和不动点定理作为研究工具,由算子的不动点定理推导出了一类非线性二阶微分方程组具有唯一一组解的不动点定理,降低了非线性算子具有不动点的条件,拓宽了研究二阶微分方程组的方法.
锥;边值问题;单调迭代序列
1 预备知识
随着非线性科学的发展,在过去的十年中,非线性泛函分析在科学研究领域扮演者越来越重要的角色.作为非线性泛函的一个分支,非线性算子理论在各个科学领域的到了广泛的研究和推广,尤其是非线性算子理论在非线性微分方程积分方程的研究领域得到了极大的研究和推广[1].众所周知在理论研究和应用方面,非线性算子不动点的存在性和唯一性是非常重要的,许多学者针对这个问题进行了研究,如在参考文献[2,3,5]中,作者研究了形如A(x)=x或者A(x,x)=x的不动点定理,在上述定理中对A算子要求是全连续的,条件比较强;而对于二阶非线性微分方程组的研究相关文献很少,在这篇文章里研究一类二阶非线性微分方程组,利用算子的紧性和上下解的方法得出了算子具有唯一一组不动点的定理,降低了算子具有不动点的条件,扩展了它的应用.
为了方便研究,我们给出以下定义,设E是实的巴拿赫空间,P是E中的锥,E中的半序“≤”由锥P导出,即x≤y当且仅当y-x∈P,用θ代表E中的零元素,若集合P满足以下两个条件:
1)x∈P,λ≥0⟹λx∈P;
2)x∈P,-x∈P⟹x=θ;
则称P是E中的一个锥, 令Pc={u∈C[I,E]:u(t)≥θ,t∈I=[0,1]},则Pc是C[I,E]中的锥.对u0,v0∈C[I,E],u0≤v0,记序区[u0,v0]={u∈C[I,E]:u0(t)≤u(t)≤v0(t),t∈I},α(*)表示非紧性测度.
这篇文章我们主要讨论以下巴拿赫空间E中二阶微分方程组的两点边值问题(BVP):
(1)
其中t∈I,f,g∈C[I×E×E,E],x0≤x1,y0≤y1,对B⊆C[I,E],t∈I,记
B(t)={u(t):u∈B}.
为了更好的讨论(1)中的二阶非线性两点边值问题,首先我们考察巴拿赫空间E中二阶线性微分方程组的两点边值问题(LBVP)
(2)
其中M>0,N≥0,ξ,η∈C[I,E].
2 几个引理
引理2.1[2]设w∈C2[I,E],满足
w″(t)≤Mw(t),w(0)≥θ,w(1)≥θ,其中M>0,则w(t)≥θ,t∈I.
(3)
引理2.2[2]设M+N<4,其中M>0,N≥0,则LBVP(2)有唯一解.
引理2.3[3](u,v)∈C2[I,E]×C2[I,E]是BVP(1)的解的充要条件是
(u,v)∈C[I,E]×C[I,E]是下列非线性积分方程组的解:
(4)
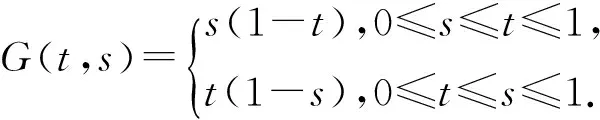
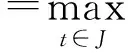
3 结论
定理3.1 设u,v∈C2[I,E]满足
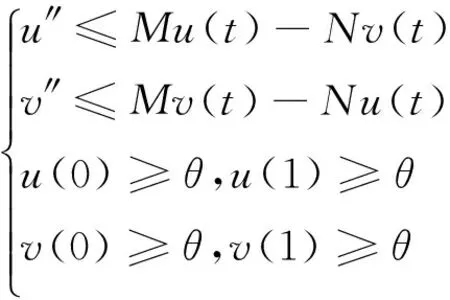
(5)
其中M>0,N≥0,M>N,则u(t)≥θ,v(t)≥θ,t∈I.
证明:令w(t)=u(t)+v(t),t∈I.由(5)知道:
w″(t)≤(M-N)w(t),w(0)≥θ,w(1)≥θ,
于是由引理2.1可以知道w(t)≥θ,t∈I.即u(t)+v(t)≥θ,t∈I.
(6)
再由(5)和(6)式,
u″(t)≤(M+N)u(t),u(0)≥θ,u(1)≥θ,
v″(t)≤(M+N)v(t),v(0)≥θ,v(1)≥θ,
因此,由引理2.1可以知道,u(t)≥θ,v(t)≥θ,t∈I.证毕.
定理3.2 设P⊂E是正则锥并且假设以下条件被满足,
(H1)存在u0,v0∈C2[I,E],u0(t)≤v0(t),t∈I,使得
-u″0≤f(t,u0,v0),u0≤x0,u0(1)≤x1,
-v″0≤g(t,v0,u0),v0≥y0,v0(1)≥y1.
(H2)存在常数M≥0,N≥0,L≥0,对任意的ui,vi∈[u0,v0](i=1,2),u2≥u1,v1≥v2,t∈I,有
f(t,u2,v2)-f(t,u1,v1)≥-M(u2-u1)-N(v2-v1),
g(t,u2,v2)-g(t,u1,v1)≥-M(u2-u1)-N(v2-v1),
g(t,u2,v2)-f(t,u1,v1)≥-M(u2-u1)-N(v2-v1).
(H3)M>N,M+N<4.
则BVP(1.1)有唯一一组解(u*,v*)∈[u0,v0]×[u0,v0],并且存在单调迭代序列
{un},{vn}⊂[u0,v0],使得{un(t)}和{vn(t)}关于t∈I分别一致收敛于u*(t)和v*(t),更进一
步,{un(t)}和{vn(t)}满足
un(t)=x0+t(x1-x0)
(7)
vn(t)=y0+t(y1-y0)
(8)
u0≤u1≤…≤un≤…≤u*≤v*≤…≤vn≤…≤v1≤v0.
(9)
证明:对任意(ξ,η)∈[u0,v0]×[u0,v0],由条件(H3)和引理2.2可以知道,LBVP(2)有唯一解(u,v)∈C2[I,E]×C2[I,E].
定义算子A(ξ,η)=(A1(ξ,η),A2(η,ξ))=(u,v).
令un=A1(un-1,vn-1),vn=A2(vn-1,un-1),(n=1,2,…).
显然,由引理2.3可知{un},{vn}满足(7)和(8)式,以下用归纳法证明
un-1≤un≤vn≤vn-1,n=1,2,…
(10)
由(H1)和(H2),有
(u1-u0)″(t)≤M(u1-u0)-N(v0-v1)
(u1-u0)(0)≥x0-x0=θ,(u1-u0)(1)≥x1-x1=θ,
(v0-v1)″(t)≤M(v0-v1)-N(u1-u0),
(v0-v1)(0)≥y0-y0=θ,(v0-v1)(1)≥y1-y1=θ,
(v1-u1)″(t)≤M(v1-u1)-N(v1-u1),
(v1-u1)(0)=y0-x0≥θ,(v1-u1)(1)=y1-x1≥θ.
因此,由引理2.1和定理3.1可知,u0≤u1≤v1≤v0.
假设un-1≤un≤vn≤vn-1.由(H2)得
(un+1-un)″(t)≤M(un+1-un)-N(vv-vn+1),
(un+1-un)(0)=x0-x0=θ,(un+1-un)(1)=x1-x1=θ,
(vn-vn+1)″(t)≤M(vn-vn+1)-N(uv+1-un),
(vn-vn+1)(0)=y0-y0=θ,(vn-vn+1)(1)=y1-y1=θ,
(vn+1-un+1)″(t)≤(M-N)(vn+1-un+1),
(vn+1-un+1)(0)=y0-x0≥θ,(vn+1-un+1)(1)=y1-x1≥θ,
因此,再由引理2.1和定理3.1可知,un≤un+1≤vn+1≤vn.故对任何自然数n,不等式
(11)
式成立.再利用(10)式得到u0≤u1≤…≤un≤…≤vn≤…≤v1≤v0.
(12)
在上述条件下我们再定义U={un},V={vn},U(t)={un(t)}⊂E,V(t)={vn(t)}⊂E,t∈I.所以U,V⊂[u0,v0],因为P⊂E是空间中的一个正则锥,所以由正则锥的性质Pc⊂[I,E]是空间中的一个正规锥.因此,U,V都是C[I,E]空间中的的有界集.由条件(H1)和(H2)并利用定理易证,U和V在区间I上都是等度连续的集合.
由Pc⊂[I,E]的正规性,可以证明,{un},{vn}在I上分别一致收敛于u*,v*∈[u0,v0],在(7)和(8)中令n→+∞,我们有:
(12)
即(u*,v*)是非线性微分方程组的(4)的解,由极限性质知是唯一一组解,再由上面已知引理2.3得到(u*,v*)∈[u0,v0]×[u0,v0]是巴拿赫空间中二阶非线性微分方程组两点边值问题(1)的一组解,且具有唯一性,且上述不等式(10)成立,证毕.
[1] 孙经先.非线性泛函分析及其应用[M].北京:科学出版社,2007
[2] Suzuki T.Characterizations of Fixed points of nonexpansivem appings[J].Int JM athSci,2005:1723-1735
[3] 蒋秉华,张 敏.不动点定理的应用[J].德州学报,2004,21(5):76-79
[4] 吴幼明,王向东,岳珠峰.一类二阶微分方程组的通解[J].汕头大学学报(自然科学版),2007(3):15-20
[5] 谭长明,龙 丽.不动点定理在方程解方面的应用[J].吉林师范大学学报(自然科学版),2006(3):83-85
The Two-Point Boundary Value Problems for the Systems of Second Order Nonlinear Differential Equations
Zhou Bibo,Zhang Runling
(Department of Mathematics Lvliang University, Lvliang 033000,China)
By using the cone stretching method,To study the two-point boundary value problems for the systems of second order nonlinear differential equations.Some new results are obtained, some relevant results are extended and improved.
cone theory; completely continuous operator; banach space
2014-10-28
山西省吕梁学院自然科学校内青年基金项目(2RXY201306).
周碧波(1978-),男,山西运城人,吕梁学院数学系助教,主要从事非线性泛函分析研究.
1672-2027(2015)01-0005-04
O175
A
