基于信号去噪的小波算法研究

王香云

(山西大学 软件工程学院，山西 太原 030013)

基于信号去噪的小波算法研究

王香云

(山西大学 软件工程学院，山西 太原 030013)

小波作为一种数学函数，被应用在很多领域，从信号去噪的角度对小波进行分析研究。首先给出小波的理论介绍，接着在matlab中通过实验对前面的理论进行进一步的阐释，最后鉴于FPGA的查找表的特点和DA算法的思想，硬件实现小波算法。

小波；信号去噪；查找表

0 引言

噪声在现实中无处不在，噪声通常认为是夹杂在有用信号中的无用成分，而噪声的存在对信号的检测、特征提取、信号的分析与处理都有很大的影响，所以能否对信号进行很好的去噪对后续的信号处理起着关键的作用。传统的去噪都是基于频域的，即把信号从现实当中的时域空间变换到方便处理数据的频域空间，然后根据噪声和有用信号在频域空间中表现出的不同特性，分别给予不同的处理，从而滤除噪声[1]。但是，传统去噪法不能同时具备频率和时间分辨率的特性，虽然通过加不同的窗函数，具有了时频特性，但是因为窗函数的关系，部分频率分辨率会损失，同时窗的大小也制约着时间分辨率。而小波变换是科恩类变换，变换时通过核函数将信号函数展开，因为核函数具有时频特性，所以小波也就具备了时间和频率分辨率的特征。本文以信号处理为基础，研究了小波算法在信号去噪中的应用。

1 小波算法介绍

小波简单的说是一种数学函数，并且这种函数不像傅里叶函数只有正弦、余弦，而小波函数不具有唯一性，只要这种函数满足小波基的数学特性，紧支性、对称性、正则性等，这种函数就可以作为一个小波基。图1为正弦波与小波示意图。除了自己定义小波基函数外，在MATLAB中，小波基函数也有很多，那么在处理特定问题时，到底应该选用那一种小波基函数，目前没有一个标准性的定论。对于同一个问题，选用不同的小波基，得到的信号特征，分析的结果也不一样，所以在小波应用中，最优小波基的选取是很关键的一步。要清楚待处理信号的类型、特征，然后通过反复的实验或经验来选择最优小波基。

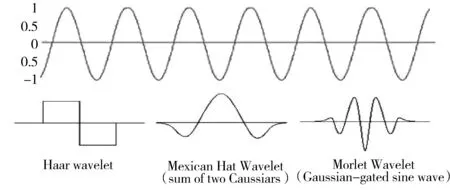
图1 正弦波与小波示意图

2 小波去噪的原理

从数学的角度看，小波去噪是函数逼近的问题，也就是根据一定的准则，在父小波和母小波平移和伸缩所形成的函数空间中，找出对原信号的最佳近似。信号去噪的过程也是实际信号空间变换到小波函数空间寻找最佳映射的过程。

从信号处理的角度看[2]，小波去噪是信号滤波，类似于低通滤波，但是小波和低通滤波相比较而言，它的优势在于去噪后能很好地保留信号的细节，所以又优于传统的低通滤波。因此，小波去噪实质上是低通滤波和特征提取的综合应用，其流程框图如图2所示。

图2 小波去噪流程框图

小波是建立在多分辨率、多尺度分析基础上的新兴算法，小波去噪的基本原理[3]如图3所示，即根据噪声与信号在小波域空间形成的小波分解系数具有不同强度分布，然后将噪声对应的小波系数按照一定的算法进行处理，有用信号的小波分解系数保留下来，然后将所有小波系数通过小波重构的方式，得到有用信号。小波去噪的方法有很多种，有模极大值去噪、阈值去噪、去相关性去噪等。本文采用的是阈值去噪。阈值去噪理论认为：信号经小波分解后，有用信号的能量集中在有限的幅值比较大的系数中，而噪声一般分散在幅值较小的系数当中，所以通过选取合适得阈值而对噪声系数进行萎缩，从而达到滤除噪声的目的。

图3 小波去噪基本原理图

3 小波去噪的MATLAB实现

3.1 噪声信号的生成

在MATLAB 7.0中通过LOAD函数装载了一个携带高斯白噪声的信号，信号如图4所示。在图中，横坐标是点数，共有1 024个点，纵坐标是信号的幅值强度大小，图5是噪声信号的频谱图，由图可知，频率变化主要集中在0～50 Hz。

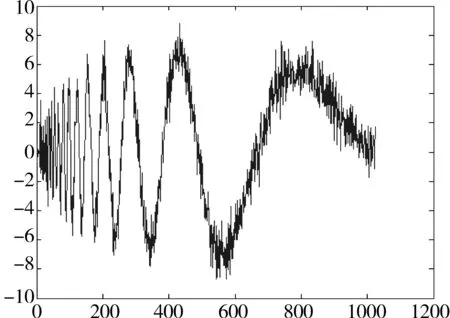
图4 含有高斯白噪声的信号

图5 噪声信号的频谱图

3.2 信号的去噪

分别设计了低通滤波器和小波变换对图4中的信号去噪，去噪效果如图6、图7所示。由图6可看出，低通滤波器在滤波时把所有的高频信号都过滤了，不仅包括高频的噪声信号，同时把信号前面的部分有用高频信号也滤掉了。图7是用不同的小波基对噪声信号进行阈值去噪处理后的结果，分别运用sym4和db4两种小波基都对噪声信号进行了4层分解，并且每层用不同的阈值对小波系数进行削切，阈值函数采用了软阈值的方式。由图7可看出小波在去掉噪声的同时，能很好的保留原始信号的高频信息，这就是小波的优势。小波能对信号进行多尺度分解，能对信号的细节部分进行很好的处理，被称为数学上的“显微镜”，并且去噪后信号的光滑性和相似性都比传统的滤波效果要好。仔细观察图7中的两幅图，可以看出采用不同的小波基对同一信号进行处理，去噪后的效果不一样，采用sym4小波基对信号进行去噪后，能很好的逼近原始信号。所以，最优小波基的选择在小波应用中是很重要的一步。

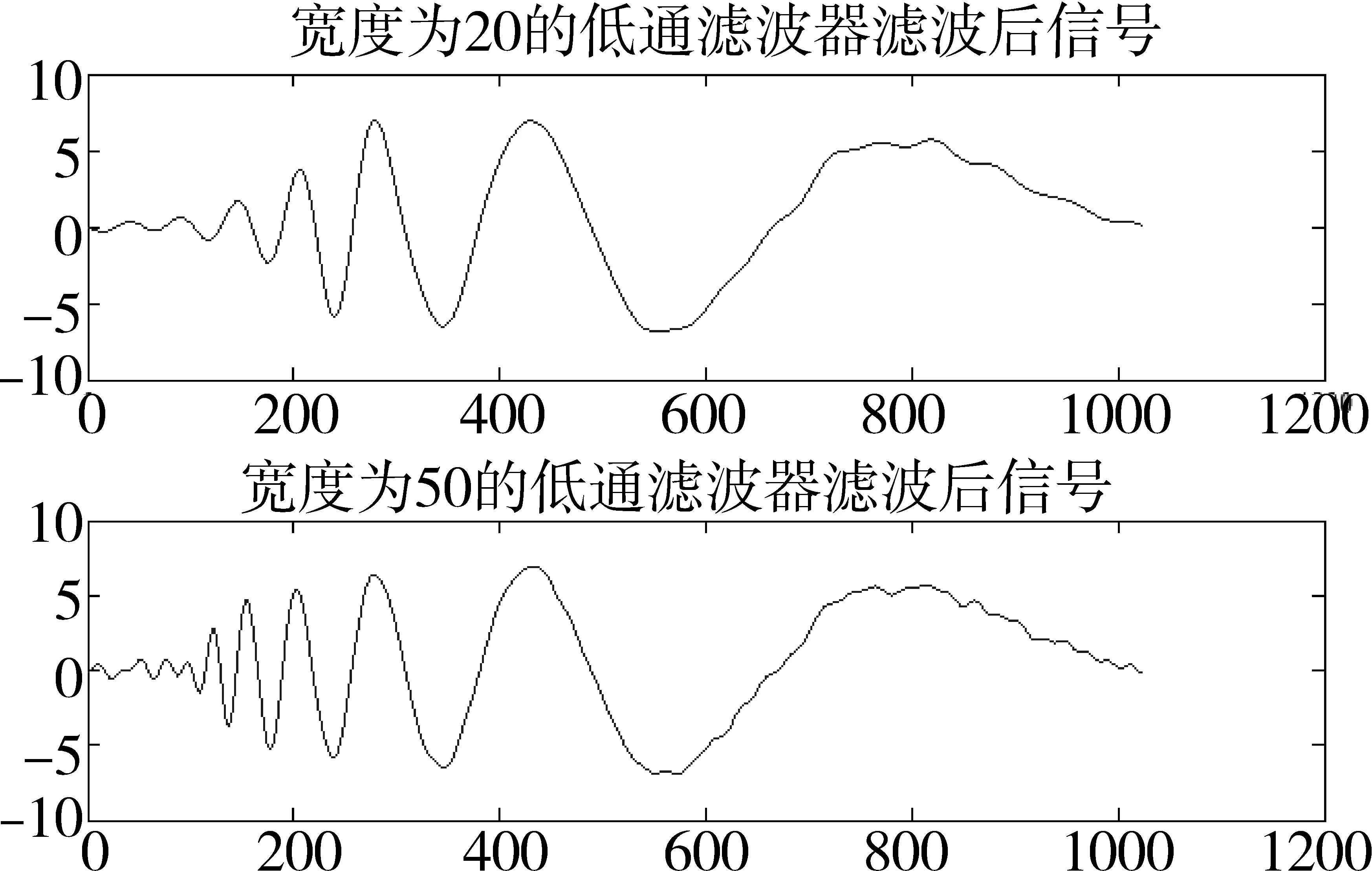
图6 低通滤波器滤波后信号信号

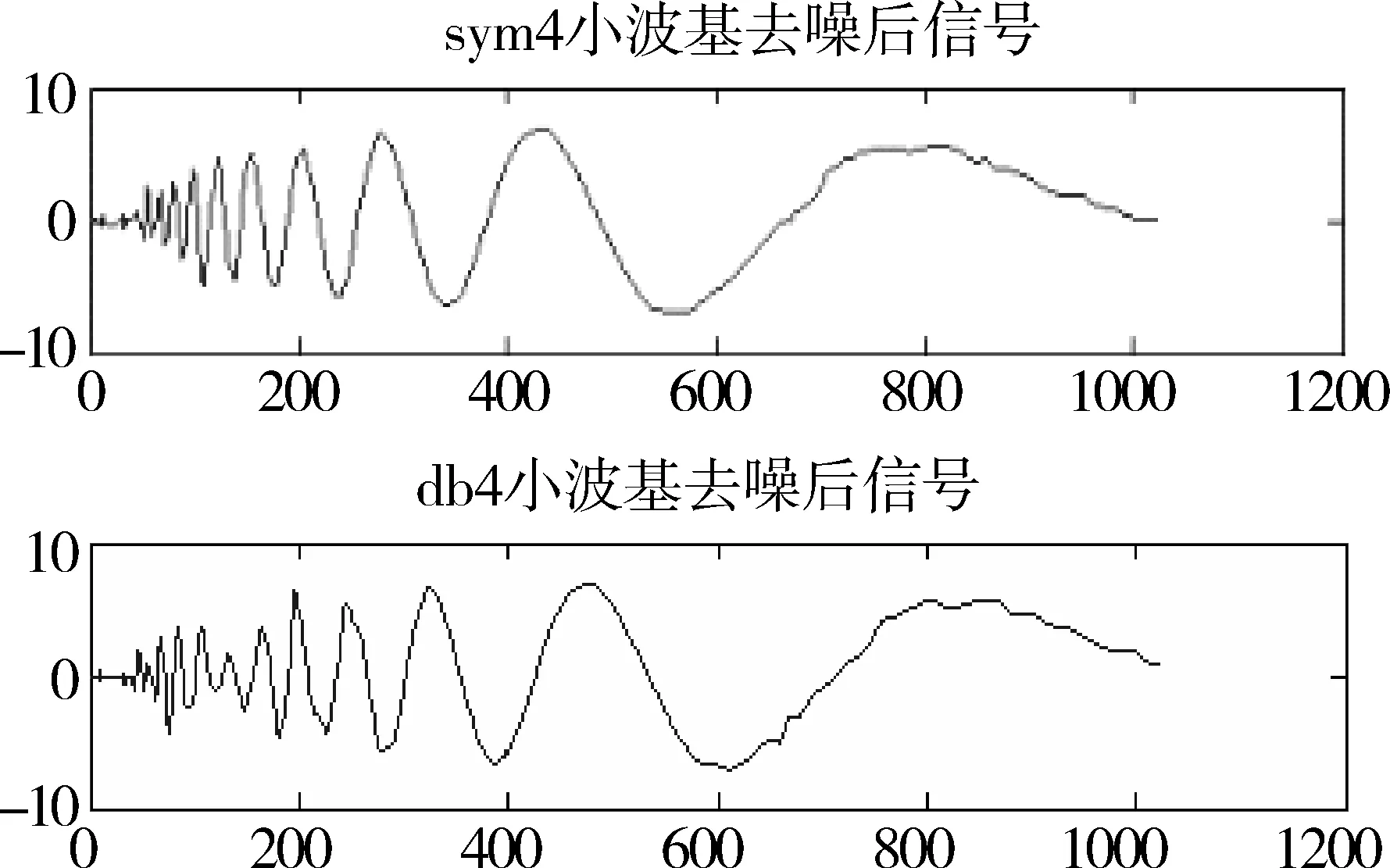
图7 小波去噪后信号

4 小波去噪的硬件实现

4.1 FPGA的查找表结构

FPGA是基于查找表结构的PLD器件，称为现场可编程门阵列，和专用集成电路(ASIC)相比，它是一种半定制电路，既克服了专用定制电路的局限性，又在门电路数目上超越了原有可编程器件.FPGA通过烧写文件，改变查找表的内容，实现对FPGA的重复配置.比如电路中有n个输入，无论执行什么运算，最多有2n种情况，事先把所有的真值表放进LUT中，然后输入一个信号就相当于输入一个地址进行查表，根据地址找出对应的内容，然后输出即可.就相当于计算机在执行程序时，无论是取指令还是数据，都是根据程序计数器中的地址在对应的存储空间中找到对应的内容.

4.2 分布式算法

分布式算法首次提出是在30多年前，但一直没有受到重视，直到FPGA的查找表结构发明后，才被有效地应用在滤波器的设计中.

设一个内积,将x[n]按机器数展开成，设M为每次抽样的数量化位宽，x[n]的第m位用xm[n]表示，x的第n次采样用xm[n]表示，则内积y可以表示为：

把c[n]·xm[n]写成函数的形式，y表示成：

函数实现就是利用一个LUT实现映射.即字宽为2N，设定程序的LUT接收一个N位输入向量]，输出为.由相应的二次幂加权并累加得到各个映射.利用如图8所示的移位加法器就能够有效地实现累加[1].当N太大时，可以考虑用多个ROM表，以并行的方式进行查询，提高速度，如图9所示.

4.3 小波的快速算法——Mallat分解重构算法[4]

Mallat算法是小波变换的快速算法，就相当于傅立叶变换中的FFT，Mallat分解算法公式为：

算法公式为:

(1)

Aj,k,Bj,k分别是逼近信号和细节信号的向量形式,即低频信号和高频信号部分．j表示分解的层数,h,g是分解滤波器组抽头系数序列．将上式转换成下面表达式:

(2)

Mallat重构算法公式为:

h′(n)和g′(n)是h(n)和g(n)的倒序序列．

将Mallat算法的公式根据DA算法的思想计算便可以得到一个ROM表格，这个表格以输入点数的bit位值为位地址，然后根据地址来查询取数.

小波的快速算法就是将信号通过滤波器组分解成低频部分和高频部分，然后将每层的低频部分进行分解，分解成下一层的低频和高频部分，小波阈值去噪认为噪声信息是在高频部分，所以通过对高频部分进行小波的阈值去噪处理，再通过重构，将低频信息和处理后的高频信息经过一层一层的重构得到去噪后的原始信号[2].

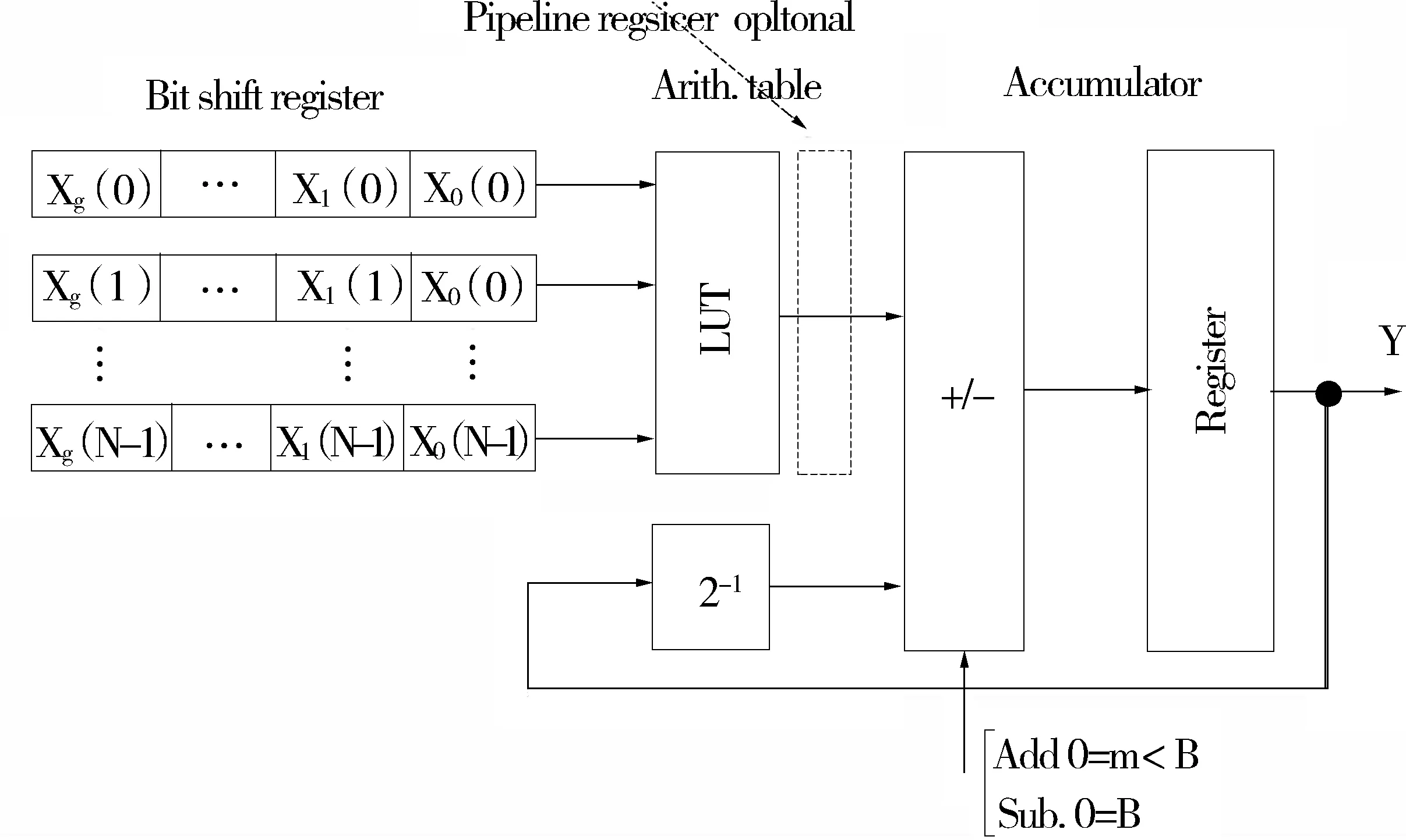
图8 低通滤波器滤波后信号信号

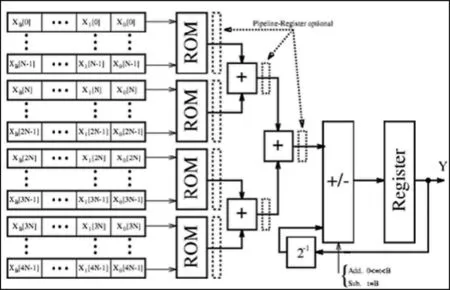
图9 小波去噪后信号

4.4 FPGA实现

在Matlab中，经过多次试验得出用sym4小波基得到的信号去噪信噪比最大，因此这里采用sym4小波基对信号作了4层分解，通过wfilters函数得到滤波器系数组，系数集放大后如表1所示.并用Matlab生成对应的DA查询ROM表，生成.coe文件，在.coe文件中，采用了十六进制数据，在ISE10.1中将其加载到FPGA的内部ROM中，通过数据的位值来查询取数.

表1 分解重构系数表

在FPGA中通过DDS，ISE10.1中自带的IP核生成一个带有噪声的方波信号，如图10所示，将噪声信号数据运用小波分解模块，得到各层的高低频分解系数，然后存到对应的ROM中，对高频系数通过阈值函数处理，这里的阈值函数采用了软阈值函数,阈值的选取采用通用阈值的方法.得到去噪后的系数后，再通过小波重构，得到去噪后的信号如图11所示.图中横坐标是点数，综坐标是信号的强度大小.由图11可以看出，经过小波去噪后，去噪效果良好.

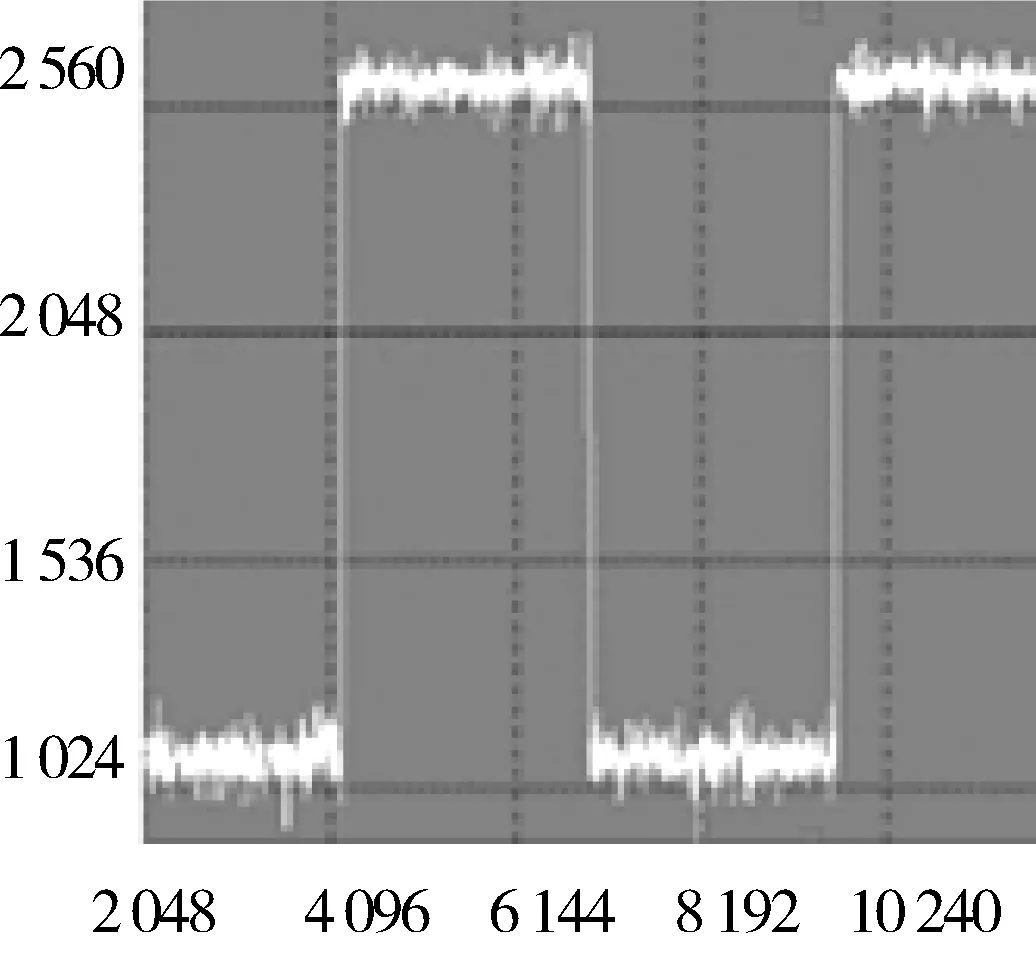
图10 噪声信号

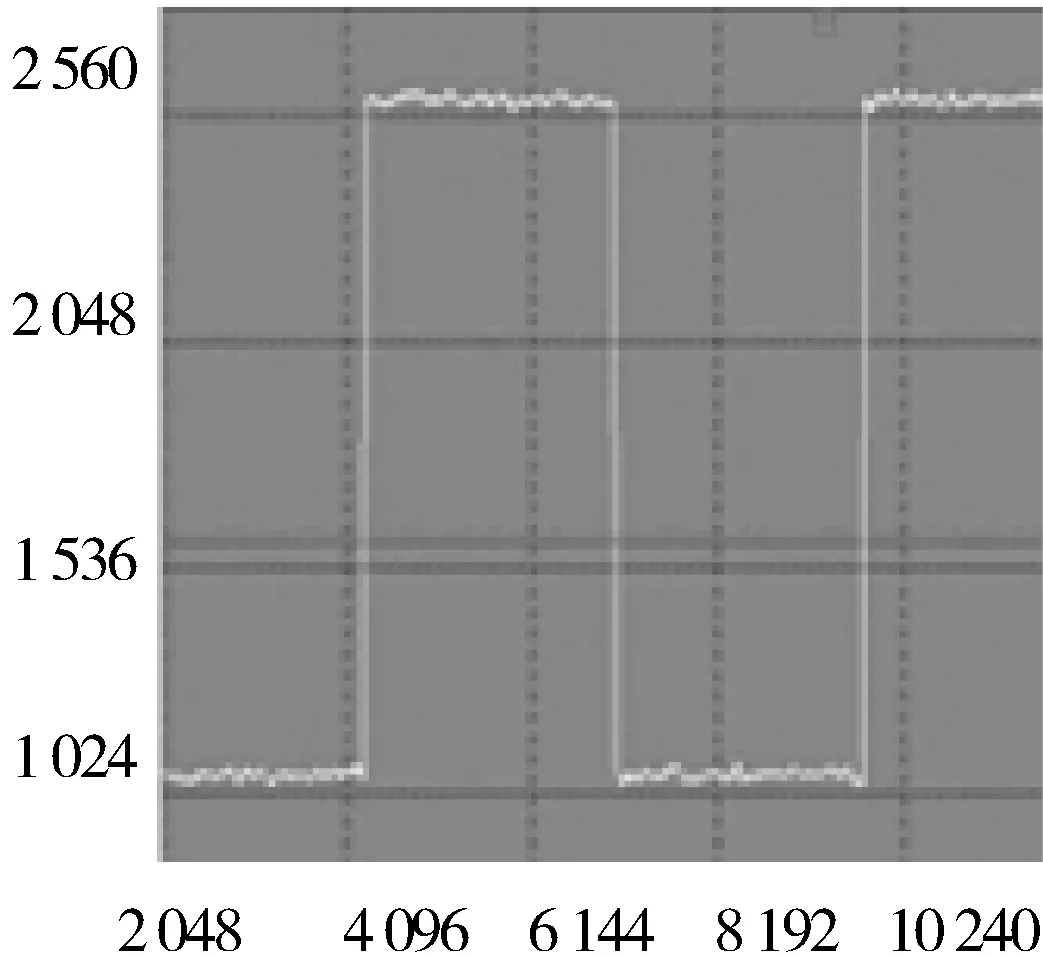
图11 小波去噪后信号

5 总结

小波变换是一种新型的变换方法，能对数据进行多层次的分解，对数据的细节部分进行更好的处理，鉴于它的时频特性，以及多分辨率性，在很多应用领域都有着广泛的应用.

[1] 刘明珍.基于DDS的DPSK调制解调软件无线电实现[D].上海:复旦大学,2008

[2] 鲍 文，周 瑞，李 宁,等.采用非降采样第二代小波变换的信号降噪方法[J].中国电机工程学报,2008(20):82-87

Study on Wavelet Algorithm Based on the Signal Denoising

Wang Xiangyun

(Software Engineering College of Shanxi University，Taiyuan 030013, China)

As a mathematical function,wavelet is applied in many fields.Wavelet is analyzed from the signal denoisingin this article.Firstlythe theory of wavelet is introduced, and then throughexperimentin the MATLAB the previous theoryis furtherexplained.In the end,in view of the lookup table characteristicsof FPGA and the DA algorithm,wavelet is realized by hardware.

wavelet;Signal denoising; lUT

2014-09-25

2013年科技厅基金资助研究项目(2013091002-0108).

王香云(1979-)，女，山西怀仁人，硕士，山西大学软件工程学院讲师，主要从事嵌入式研究.

1672-2027(2015)01-0033-05

TN911

A