ITER条件下高能量粒子对一种新型离散阿尔芬本征模的影响
2015-03-01郭新苗胡双辉
郭新苗 胡 林 胡双辉
(贵州大学理学院物理系,贵州 贵阳 550025)
物理实验
ITER条件下高能量粒子对一种新型离散阿尔芬本征模的影响
郭新苗胡林胡双辉
(贵州大学理学院物理系,贵州 贵阳550025)
摘要离散阿尔芬本征模是托克马克中存在的一种模式,它具有准边缘不稳定性,能被高能量粒子激发成不稳定模式.国际热核实验反应堆(International Thermonuclear Experimental Reactor,ITER)的设计运行有感应方案、稳态方案和混合方案,文中将在稳态方案下结合电流驱动方式来探讨αTAE的不稳定性.本文主要介绍 ITER实验设计运行条件,并据此探究ITER中的αTAE(α-induced toroidal Alfvén eigenmode,α是表示等离子体压强梯度大小的一个参数)及其由高能量粒子激发的不稳定性,结果表明在ITER中能够存在这种αTAE,且能够被高能量粒子激发成为不稳定模式.
关键词磁约束聚变;运行模式;阿尔芬波;高能量粒子;不稳定性
EFFECTS ON αTAE BY ENERGETIC PARTICLES IN ITER OPERATION
Guo XinmiaoHu LinHu Shuanghui
(Department of Physics, College of Science, Guizhou University, Guiyang, Guizhou 550025)
AbstractThe discrete Alfvén eigenmodes existing in Tokamak reactor, are quasi-marginally stable and can be destabilized by energetic particles easily. Design of international thermonuclear experimental reactor (ITER) include three possible scenarios. They are inductive operation, steady state operation, and hybrid operation, respectively. In this work, the instability feature of α-induced toroidal Alfvén eigenmode (αTAEs) are investigated in the steady state operation with both positive and negative magnetic share. This paper is to present the ITER operations and to study instability features of the αTAE and their kinetic excitations by energetic particles in the designed operate conditions of ITER experiments. The results show that αTAE indeed exists in ITER operation and can be destabilized by energetic particles.
Key wordsmagnetic confinement fusion; operation scenario; Alfvén wave; energetic particles; plasma instability
随着科技发展,人类对能源的需求越来越大,传统能源已不能满足人们的需要,寻找开发新的能源迫在眉睫.国际热核实验反应堆(International Thermonuclear Experimental Reactor,ITER)计划就是一项多国参与研究的核聚变能源工程,其目标是要建造一个可自持燃烧(即“点火”)的托克马克聚变实验堆,来验证磁约束核聚变的技术可行性[1].它的实施结果将决定人类能否大规模地使用核聚变能.
本文针对ITER装置的实验运行条件,探讨一种新型离散阿尔芬本征模αTAE(α-induced toroidal Alfvén eigenmode,α是表示等离子体压强梯度大小的一个参数),与聚变加热或点火实验中产生的高能量粒子,满足波粒共振关系时所演变而成的阿尔芬不稳定模式.这种不稳定模式将影响装置中粒子分布并导致高能量粒子大量流失,部分流失的高能量粒子撞击托克马克器壁,将直接影响核聚变反应的正常进行.下文先介绍ITER装置的物理运行以及为改善ITER运行而采用的各种运行模式和加热方法等,再探讨ITER中αTAE在高能量粒子作用下演化而成的动理学不稳定性.
1ITER物理运行
这部分介绍ITER装置的运行条件、各种运行模式和加热方法,以及存在于托克马克装置中的阿尔芬波的基本特征.
1.1 ITER运行条件
ITER是目前世界上最大的核聚变反应装置,也是中国参与的最大的国际科技合作项目之一.表1给出了ITER装置的主要设计参数[2].对核聚变反应进行有效控制并实现核聚变反应,称为受控核聚变.但在地球上实现受控核聚变,技术难度极大,必须达到劳逊条件[3](温度×密度×能量约束时间)才能实现.首先要有高温,燃料才能被电离成等离子体,带正电的氘核和氚核才有足够的能量克服静电斥力而发生聚变反应;其次是高密度,过于稀薄的粒子之间发生碰撞或反应的几率非常小;最后必须能长时间维持等离子体高温高密的状态,使等离子体的能量损失率较小.例如,在ITER中等离子体温度要高达1.5亿摄氏度, 密度数量级在1020m-3,能量约束时间超过1s才能保证可以持续发生聚变反应.
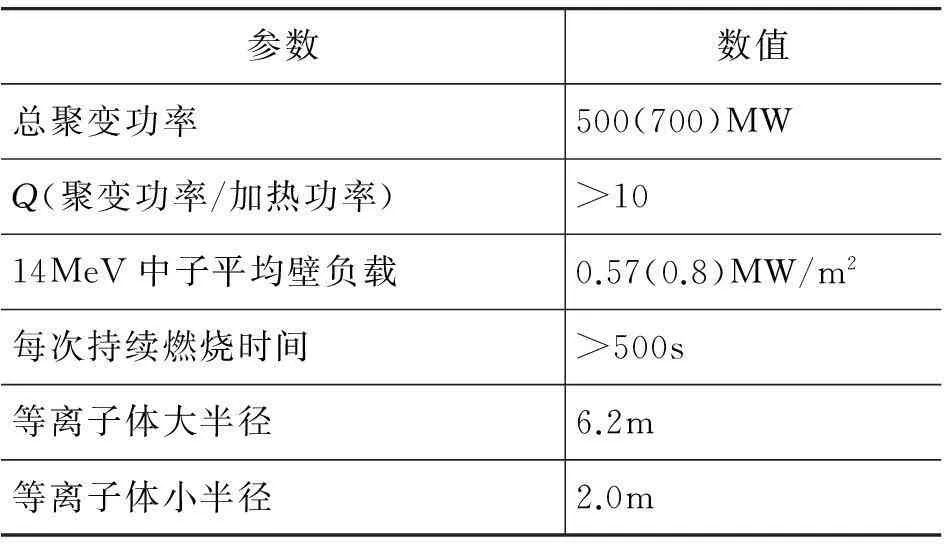
表1 ITER计划参数表
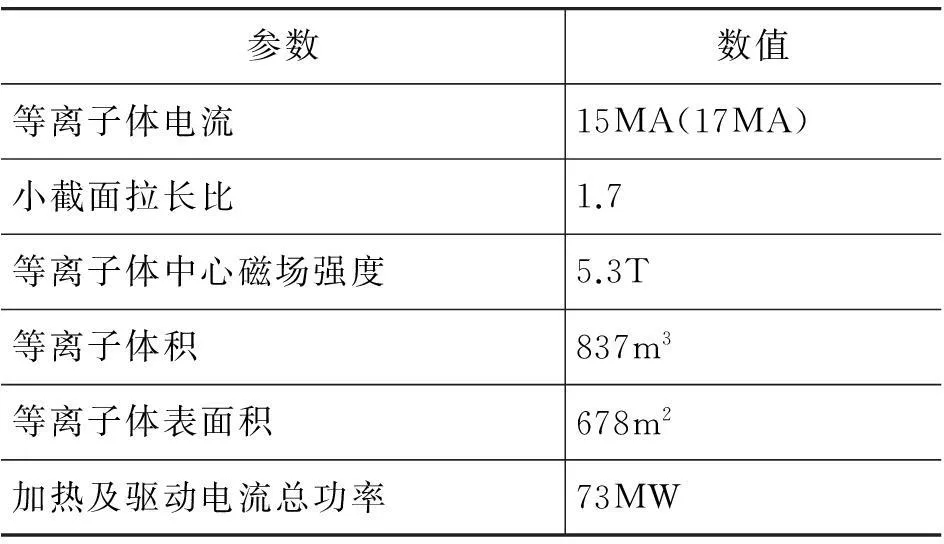
续表
为了控制这些温度高达上亿度的等离子体,科学家利用闭合磁力线的磁场来约束高温高密等离子体,即将其约束在“磁笼”中.ITER计划中设计的“磁笼”是由18节巨型的D型环向磁场线圈所组成,每一节重约360t.当强大的电流通过这些线圈时,线圈内部会产生巨大的磁场,从而将等离子体约束在磁力线附近做螺旋运动.图1为托克马克装置内部主要部件示意图[3].
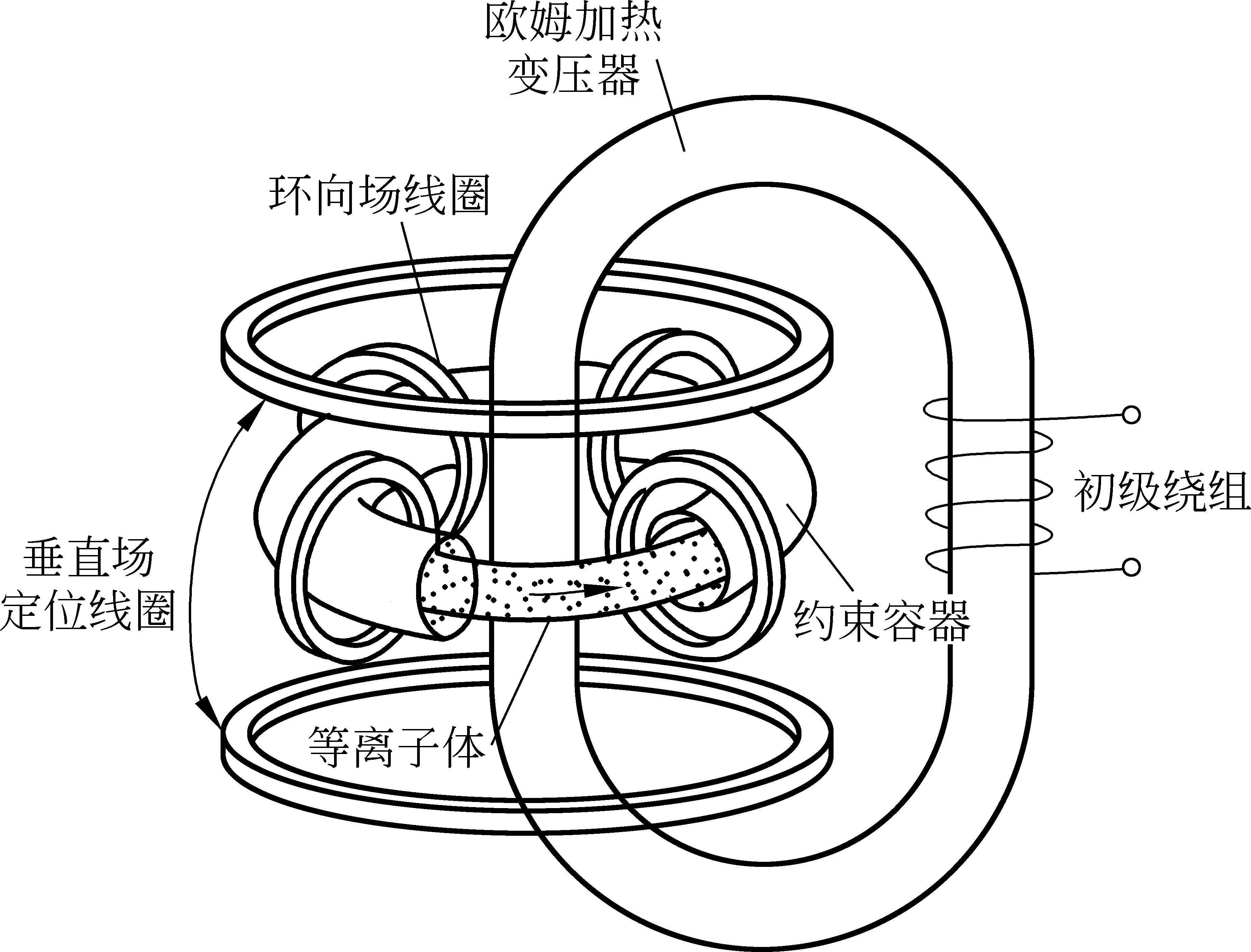
图1 托克马克装置内部主要部件示意图,摘自参考文献[3]
1.2 运行模式
将高温高密等离子体控制在磁笼中,根据电流驱动的方式,将ITER装置中运行模式分为3种,分别是感应方案、混合方案和稳态方案[1].电流驱动是指在托克马克等离子体中产生环向电流,这种电流的用途是为了使托克马克聚变反应堆连续运行.其中感应方案是指等离子体电流由磁感应驱动产生,即通过改变ITER中心螺线管中的磁通量来产生感应电流,如图1所示.感应方案预期达到的运行指标为:通过D-T聚变反应达到500MW左右的聚变能,脉冲时间维持在300~500s,得到大的聚变增益Q(聚变反应产生的能量与输入装置的能量之比)保持在10以上.传统的托克马克都是脉冲式运行即感应起电,但这种脉冲式运行显然不能使聚变堆连续地输出能量,于是人们提出了聚变反应堆的稳态运行概念.稳态方案是指完全非感应电流驱动模式,Q大于等于5,维持等离子体运行达3000s以上,获得聚变功率大于350MW[4].将两种结合在一起就是混合方案,混合方案是指驱动电流由感应方式及其以外的方式共同驱动产生等离子体电流,既有脉冲式获得高的聚变功率又可以维持聚变反应较长时间,其预期达到的运行指标为:Q在5~30之间,脉冲时间大于1000s,聚变功率达300~500MW.
1.3 加热方法
等离子体获得电流运行后,需要达到很高的温度才足以进行聚变反应,这就需要借助外界对等离子体进行加热.在等离子体中流过大电流的同时也在进行欧姆加热即初级加热,随着等离子体温度升高,其电阻减小欧姆加热作用减弱.若要达到聚变堆所需要的高温,就需要更高层次的辅助加热也就是通常所说的二级加热.通常应用的主要二级加热方法有两种:(1)中性束加热.此方法中,将一束氢或氘的高能中性粒子束射向等离子体.因为带电粒子不能横越用来约束等离子体的磁场,所以只能用高能中性离子束横越磁场,并且通过粒子间碰撞将能量传递给等离子体,从而提高等离子体的温度.(2)射频波加热,即将大功率微波注入到等离子体中.射频波的工作频率接近离子或电子在磁场中回旋的频率,等离子体从高功率射频波吸收能量.常见的射频波加热方法有电子回旋共振加热、离子回旋共振加热、低混杂加热(lower hybrid heating)等.随着温度的升高,托克马克内部的等离子体出现各种不稳定性,阿尔芬不稳定性就是其中一种.
1.4 阿尔芬不稳定性
阿尔芬波是1942年瑞典物理学家阿尔芬发现的一种因冻结效应而产生的磁流体力学波,他认为冻结在等离子体中的磁力线可作为弹性弦来处理,并预言磁化等离子体中存在沿磁力线传播的电磁横波.后来人们就把这种沿磁力线传播的电磁横波命名为阿尔芬波[5].1959年,伯克利加州大学的T K Allen等人和英国的D F Jephcott[6]第一次在实验室中探测到了阿尔芬波的存在.1975年,Rosenbluth和Rotherford[7]提出了托卡马克中高能量粒子能激发阿尔芬波,自此在世界范围内掀起了研究阿尔芬不稳定性的热潮.尤其是自20世纪80年代以来,Cheng等人[8]首先在理论上发现了环效应引起的阿尔芬本征模(toroidicity-induced Alfvén eigenmode, TAE),并预测TAE会存在于核聚变反应装置里面,能被高能粒子激发成不稳定态.
而αTAE是一种由等离子体压强梯度引发的气球模驱动势阱里的离散束缚态[9],这种束缚态本征模与阱外的连续谱解耦,耗散可以忽略不计;且它的频率是独立于环形阿尔芬频率间隙的,可以存在于频率间隙的内部和外部,具有准边缘稳定性.考虑高能量粒子以后,本来稳定的αTAE通过波粒共振会演变成为不稳定模式[10].当αTAE强烈不稳定时,可造成大量的高能量粒子离开托克马克内部而损失掉,因此研究αTAE不稳定性具有重要意义.
2ITER上的离散阿尔芬不稳定性
已有的工作[11-16]已经在理论上论述了在JT-60U、DIII-D、JT-60SA、ITER等大型托克马克装置上存在αTAE,下面探讨ITER装置中的αTAE特征及其受到高能量粒子影响而演变成的不稳定模式.
2.1 理论模型
在理想磁流体力学(magnetohydrodynamics,MHD)描述下,采用高n(n指托克马克中的环向模数)气球模表象及(s,α)平衡模型,高n剪切阿尔芬波可由下述涡旋方程来描述
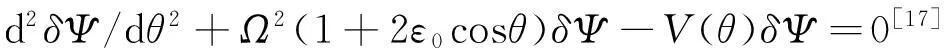
(1)
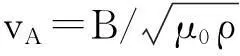
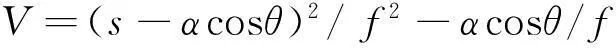
(2)
决定,其中f=1+(s θ-αsinθ)2,这里-∞<θ<∞表示沿磁场的极向角坐标.选用满足因果律的边界条件,即此处选用的阿尔芬波向外传播条件(outgoing wave boundary conditions).据此采用数值打靶法来求解上述方程的本征值Ω和相应的剪切阿尔芬本征模,以展示波能量的隧道泄漏现象.
在实际托克马克装置中阿尔芬波会受到高能量粒子的动理学作用,其中的动理学压缩是主要不稳定驱动效应.考虑高能量粒子的这个动理学压缩效应,那么在方程(1)右边即出现如下修正项[10]
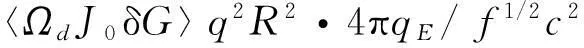
(3)
上式中〈ΩdJ0δG〉表示高能量粒子扰动分布函数在速度空间的积分贡献,qE表示高能量粒子的电荷,f和式(2)中相同.
2.2 ITER中负磁剪切下的αTAE
研究所用电子密度、电子温度、粒子密度、安全因子的数据均来自参考文献[18]中的模拟数据.文中ITER运行在稳态方案下,等离子体电流由自举电流、快波、电子回旋、低杂波共同驱动产生,根据s=r(dq/dr)/q和α=-q2Rdβ/dr在磁流体力学条件下计算得到ITER中的s、α值.此处s表征托卡马克中磁场剪切,α表示托卡马克中等离子体压强梯度,β=ne(Te+Ti)/PB是等离子体压强与磁压强之比,q是安全因子,R和r分别是托卡马克的大小半径.
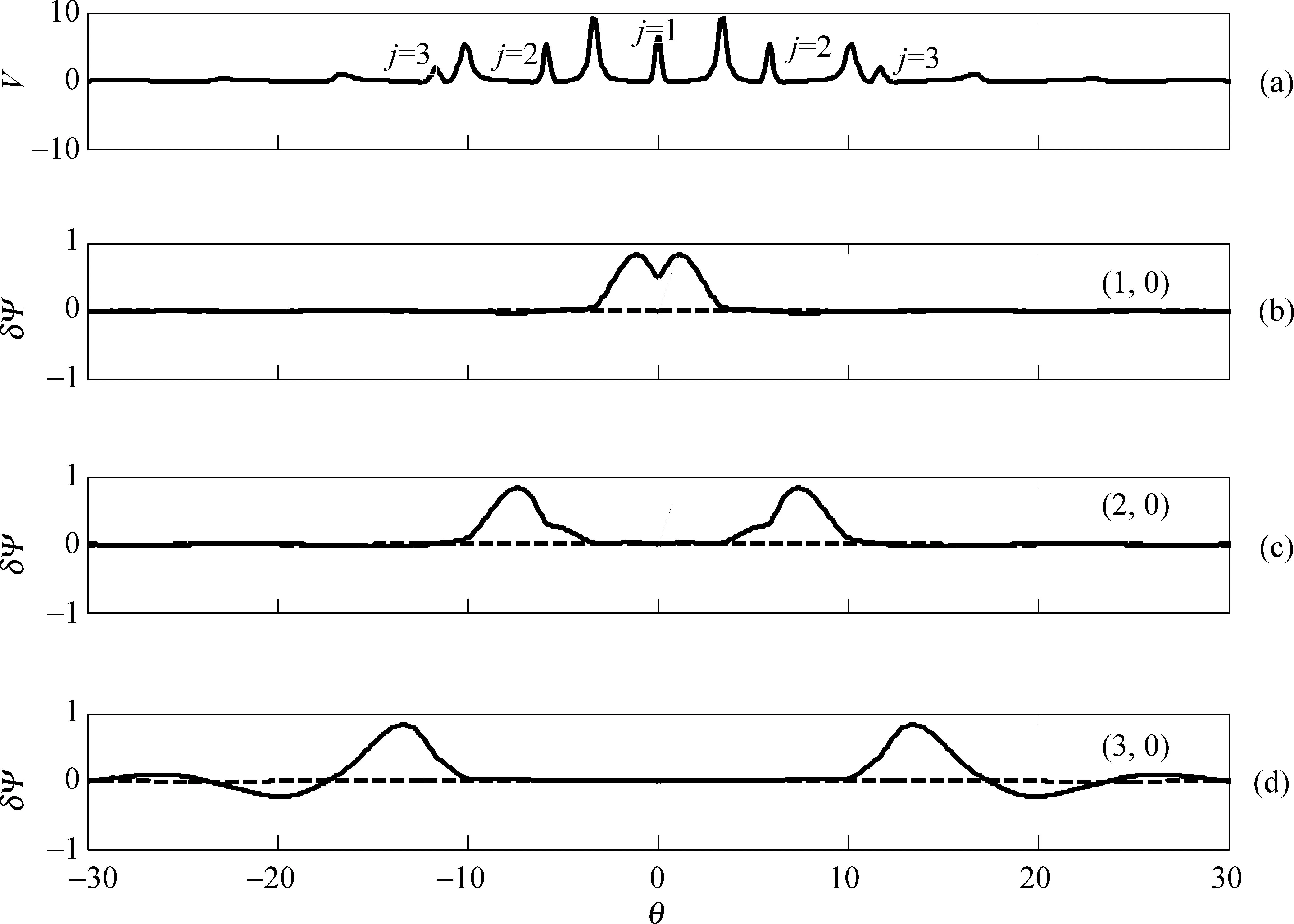
图2 s=-0.21,α=2.9时磁流体力学条件下的势阱和离散阿尔芬本征模(a)为势阱,(b)、(c)、(d)中实线表示模的实部,虚线表示模的虚部. (1,0)、(2,0)、(3,0)括号内的第一个数表示第n个势阱,0表示基态的模.
在负磁剪切下,选取s=-0.21,α=2.9,沿磁力线形成的势阱和各个势阱内部的αTAE如图2所示,横轴θ表示沿磁场的极向角坐标,图(a)的纵坐标V表示势阱,图(b)、(c)、(d)的纵坐标δψ是模结构.其中图(b)、(c)、(d)分别为(1,0)、(2,0)、(3,0)模结构,相对频率Ω分别为0.774-i6.99×10-8、0.660-i7.10×10-6和0.492-i3.04×10-7.它们的稳定与不稳定是由其对应的本征值的虚部决定的,虚部大于零增长率为正,本征模是不稳定的;虚部小于零增长率为负,本征模是稳定的,所以这些模都是MHD稳定的.在负磁剪切下,不仅在第一个气球模驱动势阱中存在αTAE,而且在沿着磁力线的多个势阱中同样存在αTAE.在负磁剪切下考虑高能量粒子,即结合方程(1)和有动理学压缩修正的方程(3)按照文献[10]中的方法来探讨αTAE的稳定性.取参数βE0=0.04,ε=0.2,LP0/R=-0.1,θb∈[100,1700],其中βE0表示高能量粒子的β标度,LP0/R表示等离子体压强的空间特征尺度,θb表示捕获粒子的回转角.在共振参量kθρA0=0.02,高能量粒子速度vE/vA0=1.9时得到了对应的动理学描述下的(3,0)模, 其相对频率为0.465+i4.16×10-3, 如
图3所示.本征模δψ是决定模结构的,而本征值的虚部表示模结构随时间的增长或衰减.从计算出来的本征值可以看出,(3,0)模在MHD条件下的本征值是衰减的,说明模结构稳定;考虑高能量粒子修正后,本征值是增长的,模结构不稳定.在MHD条件下(3,0)模的能量泄漏最多并能被激发,意味着其他的模式更容易被激发,说明在负磁剪切条件下沿着磁力线的多个势阱中存在的αTAE都可能被高能量粒子激发为不稳定模式.
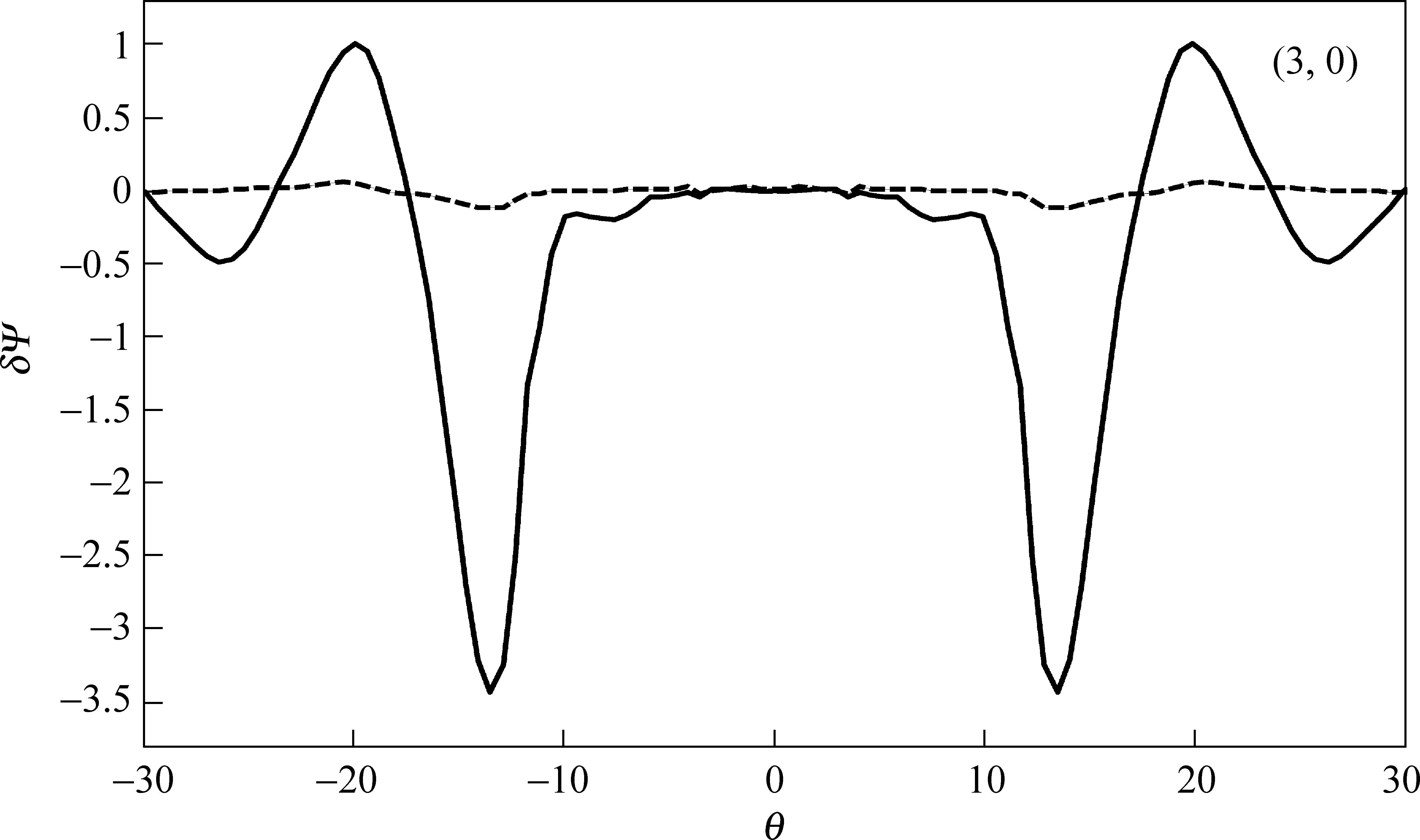
图3 s=-0.21,α=2.9时动理学描述下激发的离散阿尔芬本征模,实线表示模的实部,虚线表示模的虚部
2.3 ITER中正磁剪切下的αTAE
在正磁剪切下,选取s=0.11,α=2.4,沿磁力线形成的势阱和各个势阱内部的αTAE如图4所示.其中图(a)为沿着磁场形成的势阱,图(b)、(c)、(d)、(e)分别为阱内束缚的αTAE,(1,0)、(2,0)、(3,0)、(4,0)模的相对频率分别为0.673-i1.38×10-11、0.628-i4.84×10-11、0.535-i1.58×10-12和0.406-i9.40×10-6. 它们的虚部小于零增长率为负,所以这些模都是MHD稳定的.同样在正磁剪切下,沿着磁力线的多个势阱中存在αTAE.
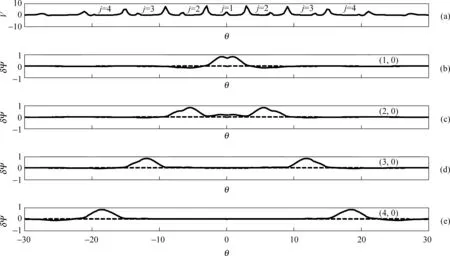
图4 s=0.11,α=2.4时磁流体力学条件下的势阱和离散阿尔芬本征模(a)为势阱,(b)、(c)、(d)、(e)中实线表示模的实部,虚线表示模的虚部. (1,0)、(2,0)、(3,0)、(4,0)括号内的第一个数表示第n个势阱,0表示基态的模.
那么考虑高能量粒子以后,在正磁剪切下,选取βE0=0.05,ε=0.2,LP0/R=-0.1,θb∈[70°,110°],在共振参量kθρA0=0.02,高能量粒子速度vE/vA0=0.7时得到了对应的动理学描述下的(4,0)模,其相对频率为0.399+i3.68×10-2,如图5所示.最外势阱中的(4,0)模能量泄漏最多仍能被激发,意味着其他势阱中的束缚态也能被激发.因此,在正磁剪切条件下,准边缘稳定的αTAE也能被激发成为不稳定模式.
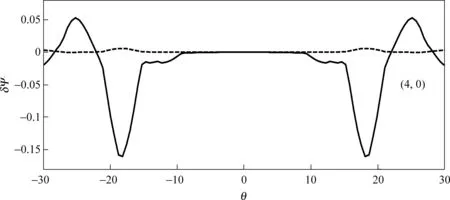
图5 s=0.11,α=2.4时动理学描述下激发的离散阿尔芬本征模(实线表示模的实部,虚线表示模的虚部)
图6表示高能量粒子影响下,αTAE的实频和增长率随共振条件的变化趋势,横轴kθρA0表示波粒共振条件的一个参量,kθ是沿着θ方向的波数,ρA0是粒子绕着磁场做回旋运动半径的一个标度,左右纵轴分别表示αTAE的实频和增长率.取参数s=0.11,α=2.4,βE0=0.05,ε0=0.2,ε=0.2,LP0/R=-0.1,θk=0.0,θb∈[70°,110°],当高能量粒子的速度vE/vA0=0.7时,kθρA0从0.02变化到0.50,得到了高能量粒子共振激发的αTAE的实频和增长率随kθρA0的变化趋势曲线.可以看出在kθρA0的较宽范围内,均有αTAE被激发而演变成的不稳定模式.
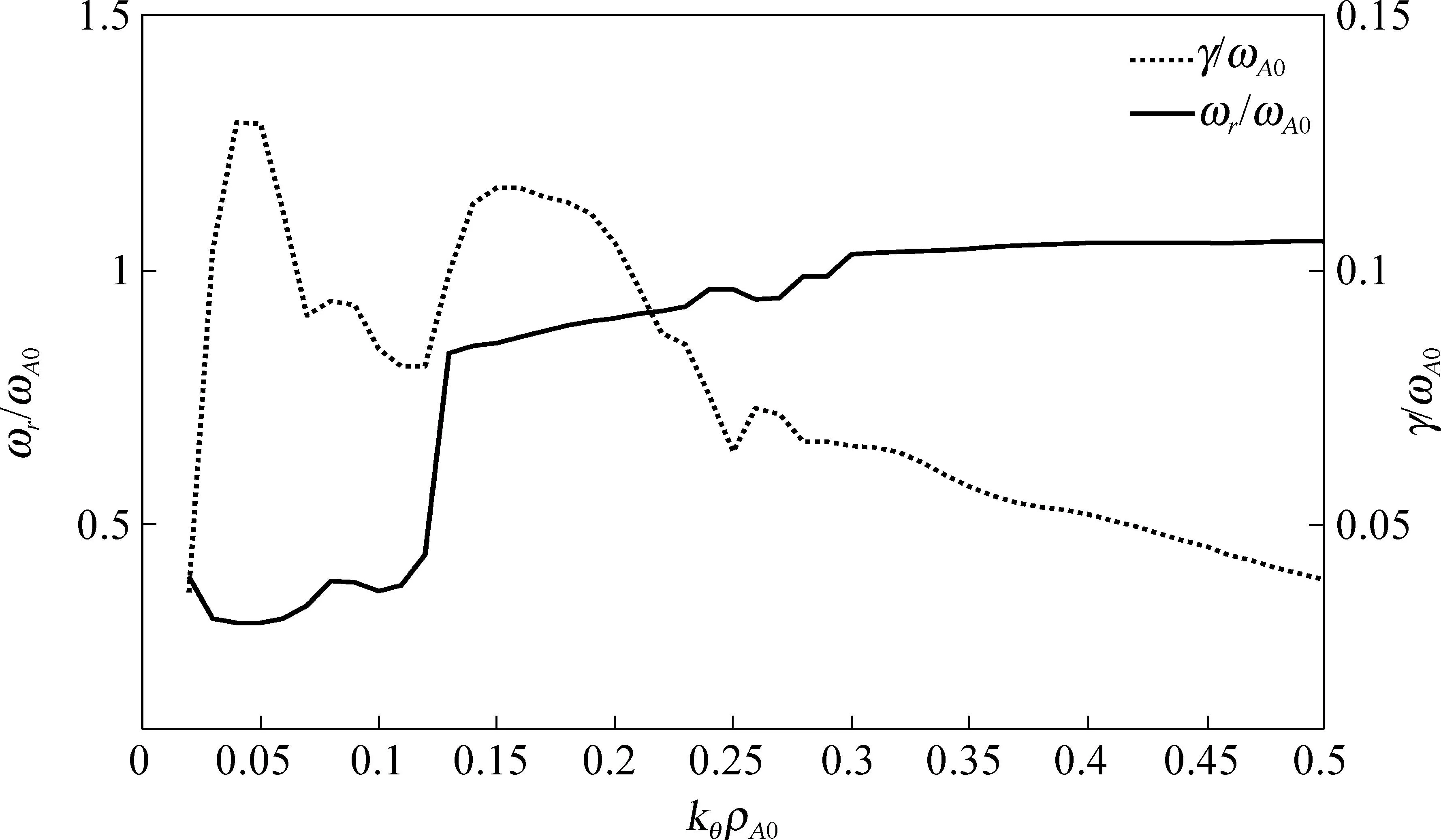
图6 vE/vA0=0.7时αTAE的实频和增长率随kθρA0的变化图(实线表示实频,虚线表示增长率)
稳态运行是托克马克所期望的运行模式,自举电流、快波、电子回旋、低杂波都可以实现ITER稳态运行.在稳态运行模式时,不论正磁剪切还是负磁剪切,这些驱动电流方式都可以产生αTAE,并且这些准边缘稳定模式都能被高能量粒子激发为不稳定模式,可见研究αTAE的稳定性特征具有重要意义.
3结语
本文介绍了ITER实验装置的运行条件及其相关的运行模式和加热方法,并在ITER运行条件下探究了αTAE这种离散阿尔芬本征模的动理学不稳定性.理论计算表明ITER中稳态运行时,在正磁剪切和负磁剪切条件下高能量粒子都能将准边缘稳定的αTAE激发为不稳定模式.在ITER将来运行过程中,随着点火和加热的进行会产生大量的高能量粒子.因此这种潜在的阿尔芬不稳定性值得深入研究,今后的工作会进一步结合ITER具体运行条件来探讨αTAE的粒子动理学行为所激发的不稳定特性及其对装置约束性能的影响.
参考文献
[1]Shimada M,Campbell D J,Mukhovatov V,et al.Chapter 1:Overview and summary[J].Nuclear Fusion,2007,47(6):1-17.
[2]张一鸣,曾丽萍,沈欣媛,等.ITER计划与聚变能发展战略[J].核聚变与等离子体物理,2013,33(4):359-365.
[3]冯开明.可控核聚变与ITER计划[J].现代电力,2006,23(5):82-88.
[4]冯开明.ITER实验包层计划综述[J].核聚变与等离子体物理,2006,26(3):161-169.
[5]Alfvén H.Existence of electronmagnetic-hydrodynamic waves[J].Nature,1942,150(3805):405-406.
[6]Jephcott D F.Alfvén waves in a gas discharge[J].Nature,1959,183(4676):1652-1654.
[7]Rosenbluth M N,Rutherford P H.Excitation of Alfvén waves by high-energy ions in a tokamak[J].Physical Review Lettres,1975,34(23):1428-1431.
[8]Cheng C Z,Chen L,Chance M S.High-n ideal and resistive shear Alfvén waves in tokamaks[J].Annals of Physics,1985,(161):21-47.
[9]Hu S H,Chen L.Discrete Alfvén eigenmodes in high-β toroidal plasmas [J].Physics of Plasmas,2004,11(1):1-4.
[10]Hu S H,Chen L.Discrete Alfvén eigenmodes excited by energetic particles in high-β toroidal plasmas [J]. Plasma Physics and Controlled Fusion,2005, 47(8):1251-1269.
[11]姚龙宝,胡双辉,王一如,等.现行托卡马克参数下的离散阿尔芬本征模[J].核聚变与等离子体物理,2012,32(1):8-14.
[12]王一如,胡双辉,姚龙宝,等.DIII-D高性能运行参数下的离散阿尔芬本征模[J].核聚变与等离子体物理,2012,32(2):140-147.
[13]孔冉,胡双辉,王帅,等.JT-60U及JT-60SA运行条件下高能量粒子激发的离散阿尔芬本征模[J].核聚变与等离子体物理,2013,33(2):113-120.
[14]Wang J,Hu S H,Dai Q P, et al.Discrete Alfvén eigenmodes in international thermonuclear experimental reactor operations with negative magnetic shear[J].Chin Phys B,2010,19(9):0952021-0952026.
[15]田换娜,胡双辉,郑义鸿,等. ITER参数下的离散阿尔芬本征模[J]. 贵州大学学报(自然科学版).2014,31(3):21-24.
[16]陈淑平,胡双辉,王一如,等.ITER不同设计方案下的离散阿尔芬本征模[J].贵州大学学报(自然科学版).2012,29(1):23-26.
[17]Chen L,Zonca F.Theory of shear Alfvén waves in toroidal plasmas[J].Physica Scripta,1995,60:81-90.
[18]Garcia J,Giruzzi G,Artaud J F,et al.Integrated modeling of ITER steady-state scenarios[J].Plasma Physics and Controlled Fusion,2008, 50(12): 124032-124039.
■
通讯作者:胡林,女,教授,主要从事大学物理教学和软物质科研工作,研究方向为软凝聚态物理.hulin53@sina.com
作者简介:郭新苗,女,硕士研究生,主要从事等离子体物理方向,研究方向为软凝聚态物理.guoxinmiao628@163.com
基金项目:国家自然科学基金(11264006),国家自然科学基金项目(11275053).
收稿日期:2014-10-08;修回日期: 2015-03-13
