对2013年高考数学中一道几何题的探究

张少华，潘永会

（遵义师范学院数学与计算科学学院，贵州遵义563002）

对2013年高考数学中一道几何题的探究

张少华，潘永会

（遵义师范学院数学与计算科学学院，贵州遵义563002）

对2013年全国高考（理科）数学卷（新课标Ⅱ卷）第三题（22）小题从作题意图、解法探索、变式探究等方面进行了研究，获得了此题的几个证明方法及一些变式。

高考；数学试题；探究

2013年高考全国理科数学卷（新课标Ⅱ卷）第（22）题是高中数学选修4-1几何证明选讲的内容。如图1所示，CD为∠ABC外接圆的切线，AB的延长线交直线CD于点D，E、F分别为弦AB与弦AC上的点，且BC AE＝DC AF，B、E、F、C四点共圆。（1）证明：CA是外接圆的直径；（2）若DB＝BE＝EA，求过B、E、F、C四点的圆的面积与外接圆面积的比值。

现对这道题从如何作出满足条件的题意图、证法探索、变式探究等方面展开研究。

1 作题意图

满足第一问条件的题意图很容易作出，而满足第二问条件的题意图，除满足第一问的条件外，还要满足DB＝BE＝EA。

分析：假设满足条件的题意图（如图1所示）已经作出。由于DB＝BE＝EA，因此，以DA为直径的圆交垂线BC于点C点，而ABC的外接圆也过C点。这样，满足条件的题意图就能正确作出。

作法：（1）作线段DA，使DB＝BE=EA，分点为B、E；（2）过B作线段DA的垂线l；（3）以线段DA的中点为圆心，1/2DA长为半径画弧交直线l于C点，连接CD、CA；（4）作ABC的外接圆；（5）过E点作CA的垂线CA交于F，连接CE，擦去辅助线，则所作图形（见图2）满足题设条件。（证明略）

2 解法探究

解法一[2]：

分析：

（2）由（1）易知，CA是ABC外接圆的直径，CE是过B、E、F、C四点的圆的直径。考虑到DB=BE= EA，立即可解。

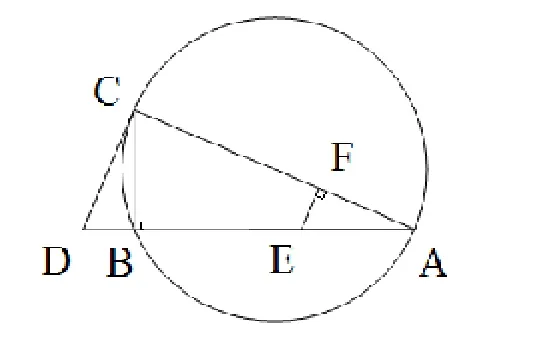
图1 证法一示意图

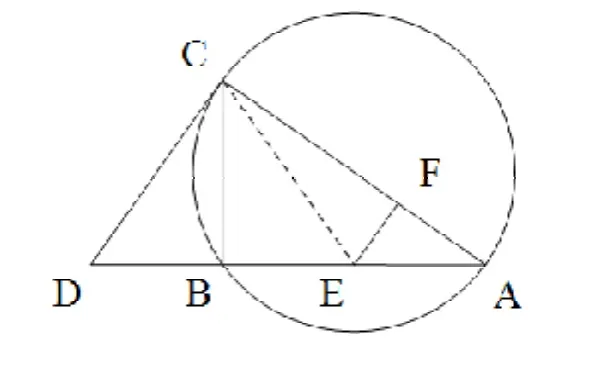
图2 解法一示意图

解题过程：

（1）证明：因为CD为ABC外接圆的切线，则∠DCB＝∠DAC，又BC·AE=DC·AF，则

所以，∠DBC=∠EFA。

又B、E、F、C四点共圆，则

∠EFA=∠CBE。

因此，∠ABC=90°，

所以，CA是ABC外接圆的直径。

（2）连接CE，由（1）知，CA是ABC外接圆直径，CE是过B、E、F、C四点的圆的直径。又DB＝BE＝EA，则

CA2＝AB AD＝6DB2,

CE2＝CD2＝DB DA＝3DB2。

因此，SBEFC:SABC＝1:2。

解法二：

分析：

（1）由证法一，CD为ABC外接圆的切线，BC AE＝DC AF，可得，BCD∽FAE，进而可得∠CDB＝∠AEF，因而，DC//EF，这样，∠EFA＝∠DCA＝90°。考虑到B、E、F、C四点共圆，则可得∠EFA＝∠CBE，因而∠ABC＝90°，故可证。

（2）由于DB＝BE＝EA，DA与BC垂直，因此，考虑以DA所在直线为x轴，BC所在直线为y轴，建立如图3所示的平面直角坐标系来解此题。

解题过程：

（2）DA所在直线为x轴，BC所在直线为y轴，建立如图3所示的平面直角坐标系，设a＞0，b＞0，由已知DB=BE=EA，因此可设D(-a,0)，B(0,0)，E(a,0)，A(2a,0)，C(0,b)。

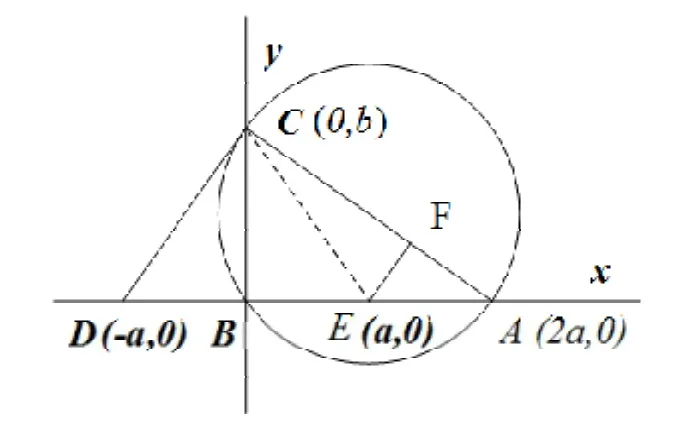
图3 解法二示意图

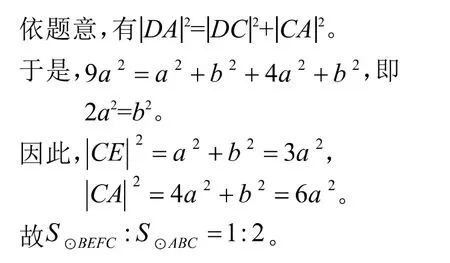
解法三：

分析：

由法二知，∠CDB=∠AEF。考虑到B、E、F、C四点共圆，则可得∠AEF=∠ACB。这样，在与中，有∠ACB=∠ADC，∠BAC=∠CAD，则立即可得∠ABC=∠ACD=90°。

解题过程：

证明：由法二知，∠CDB=∠AEF。又B、E、F、C四点共圆，则∠AEF=∠ACB。在中，有∠ACB=∠ADC，∠BAC=∠CAD，则因此，∠ABC=∠ACD=90°。所以，CA是ABC外接圆的直径。

解法四：

分析：由前法知，∠ACB=∠ADC。从而，

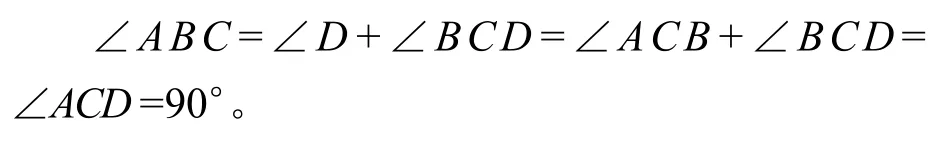
证明：略。

3 变式探究

变式[3]1：减少条件。

变式1.1：最少条件。

如图4，CD为ABC外接圆的切线，AB的延长线交直线CD于点D。（1）证明：DC2=DB DA；（2）若CB是∠DCA的平分线，证明：BC=BA；（3）若CB是∠DCA的平分线，且B为AD中点，证明：CA是外接圆的直径。

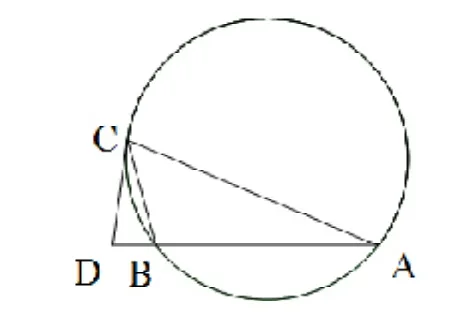
图4 变式1.1(1)示意图

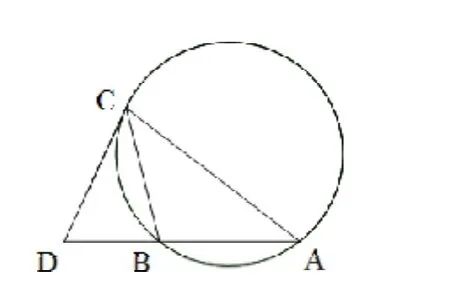
图5 变式1.1(2)示意图

分析：

（1）由于CD为ABC外接圆的切线，则∠DCB=∠DAC，从而可推得BCD∽CAD，因此可证。（2）若CB是∠DCA的平分线，则∠DCB=∠BCA=∠BAC，则立即得证。（3）若CB是∠DCA的平分线，且B为AD中点，则有BD=BC=BA，因而，∠BCD+∠BCA=90°，故可证。

解题过程：

（1）证明：因为CD为ABC外接圆的切线，则∠DCB=∠DAC，又∠BDC=∠CDA，因此，BCD∽CAD，所以

（2）证明：因为CD为ABC外接圆的切线，则∠DCB=∠DAC，又CB是∠DCA的平分线，则∠DCB=∠BCA，因此，∠BAC=∠BCA，则BC=BA。

（3）由（2）有BC=BA，又B为AD中点，则DB=BA，因此，BD=BC=BA，所以，∠D=∠BCD=∠BCA=∠BAC=45°，因此，∠ABC=90°，故CA是ABC外接圆的直径(如图6所示)。

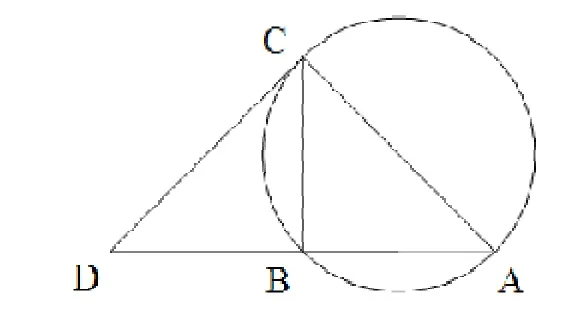
图6 变式1.2(3)示意图

变式1.2：较少条件。

如图7，CD为外接圆的切线，AB的延长线交直线CD于点D，E、F分别为弦AB与弦AC上的点，且BC AE=DC AF。证明：DC//EF。

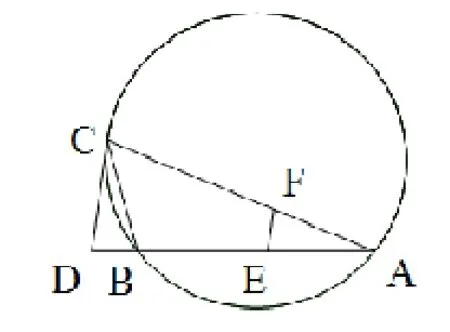
图7 变式1.2示意图

分析：由于CD为外接圆的切线，则∠DCB=∠DAC。由BC AE=DC AF，可变为从而可得进一步可得，∠BDC=∠FEA，这样，立即得DC//EF。

证明：因为CD为外接圆的切线，则∠DCB=∠DAC。

又BC AE=DC AF，则

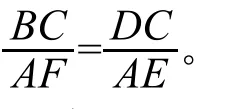
所以，∠BDC=∠FEA，

故DC//EF。

变式2：证明新结论。

如图1，CD为ABC外接圆的切线，AB的延长线交直线CD于点D，E、F分别为弦AB与弦AC上的点，且BC AE=DC AF，B、E、F、C四点共圆。证明：

（1）DC2=DB DA；

（2）CA2=AB AD；

（3）BC2=DB BA。

证明略。

变式3：变化条件。

变式3.1如图8，CD为外接圆的切线，AB的延长线交直线CD于点D，∠ACB的平分线CE交DA于E，求证：过C点且与DA切于点E的圆（小圆）也与CD相切[4]。

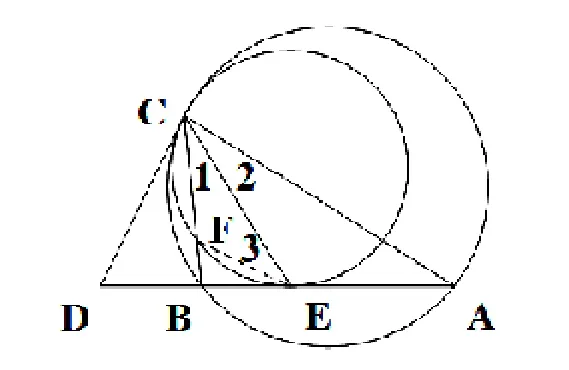
图8 变式3.1示意图

分析：只要证过点C、E的圆（小圆）与CD相切即可。

证明：设小圆BC交于F，连接EF。因为DA是小圆的切线，则∠BEF=∠1。又因CE是∠ACB的平分线，则∠1=∠2。又∠BEF+∠3=∠2+∠DAC，则∠DAC=∠3。因为CD为ABC外接圆的切线，则∠DCB=∠DAC。所以，∠DCF=∠DCB，∠DAC=∠3，即∠DCF=∠3，因此，过C点且与DA切于点E的圆（小圆）也与CD相切。

变式3.2如图9，CD为ABC外接圆的切线，AB的延长线交直线CD于点D，∠ADC的平分线分别交BC、AC交于E、F，求证：CE=CF[4]。

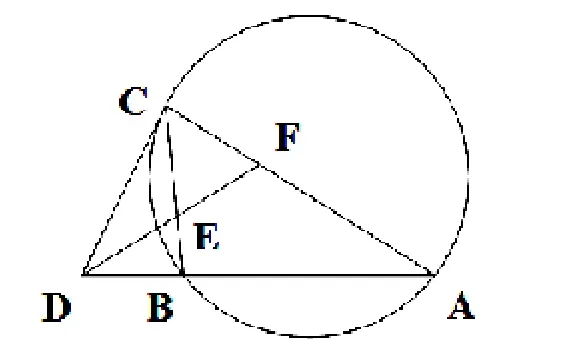
图9 变式3.2示意图

分析：要证CE=CF，只需证明它们对应的的两个角相等即可。

证明：∠CEF=∠BCD+∠EDC，∠CFE=∠FDA+∠DAC。因为CD为ABC外接圆的切线，则∠DCB=∠DAC。又DF是∠ADC的平分线，则∠EDC=∠FDA。因此，∠CEF=∠CFE，所以，CE= CF。

变式4：增加条件。

如图10，CD为外接圆的切线，AB的延长线交直线CD于点D，E、F分别为弦AB与弦AC上的点，且BC AE=DC AF，B、E、F、C四点共圆，过B作外接圆的切线BG交CD于G。证明：CG=GD。

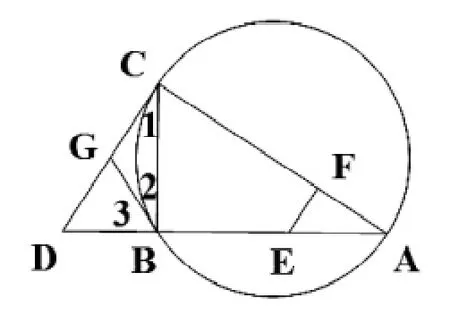
图10 变式4示意图

[1]张少华.对双圆四边形的性质的探讨[J].遵义师范学院学报, 2002,4(4):64-66．

[2]学科网.2013年高考数学试题及答案（新课标全国卷Ⅱ）[DB/OL].(2015-03-12)http://www.zxxk.com/Feature/2013gk/ showinfo.aspx?Page=5&InfoID=248457．

[3]张少华,王思聪.常微分方程教学中探究式教学法初探[J].遵义师范学院学报,2007,9(6):72-74．

[4]唐秀颖,夏明德.数学题解辞典平面几何[M].上海:上海辞书出版社,1993.575,420-421．

（责任编辑：朱彬）

A Study of One Geometrical Problem in the 2013 National Entrance Examination

ZHANG Shao-hua，PAN Yong-hui
(College of mathematics and computing science,Zunyi Normal College,Zunyi 563002,China)

This paper makes an investigation into the twenty-second problem of the math paper(science part)in the 2013 national entrance exam(the II Volume of new curriculum standard)in terms of intent,solution exploration and variation study,and some solutions to this problem as well as some variants are obtained.

national entrance exam;math problem;exploration

G424.79

A

1009-3583（2015）-0134-04

2013-06-27

贵州省基础教育科研项目（2012B280）

张少华，男，贵州遵义人，遵义师范学院数学与计算科学学院教授，硕士。研究方向：应用数学、数学教育。