模糊变结构在可重复使用运载器再入轨迹跟踪上的应用

胡钰，王华，2，任章

(1.中北大学 机电工程学院，山西 太原030051;2.北京航空航天大学 宇航学院，北京100191;3.北京航空航天大学 自动化科学与电气工程学院，北京100191)

0 引言

可重复使用运载器(RLV)的再入返回过程可分为下降段、准平衡滑翔段和末端能量管理段，其中准平衡滑翔段是最主要的飞行阶段，在此过程中，由于特殊的飞行模式、复杂的飞行包线、恶劣的飞行环境，使飞行器气动参数变化较为剧烈，呈现严重的非线性及不确定性［1］，加之对航迹角的严格要求，成为跟踪控制系统设计面临的重要问题。目前，RLV轨迹跟踪控制大多是针对在平衡点附近进行小扰动线性化后的模型采用最优控制方法设计的［2-3］，但是最优控制方法一方面对精确数学模型依赖性大，另一方面当气动参数等发生较大变化，或者工作状态发生突发偏离时，表现出鲁棒性较差的问题。

滑模变结构控制具有动态品质好、控制精度高、鲁棒性强、干扰抑制能力强的优点，成为一种控制不确定系统的有效方法［4］。

为了克服传统跟踪方法鲁棒性差的缺陷，国内外很多学者将变结构设计方法引入到高超声速飞行器轨迹跟踪中，文献［5］通过滑模控制很大程度提高了系统的鲁棒性，保证了导弹运动的精确跟踪，但是由于采用简单的趋近律造成控制变量抖振较大。本文在文献［5］的基础上，对RLV 再入参考轨迹进行纵向跟踪，滑模面采用最优化方法进行设计，保证了滑模运动具有较强的鲁棒性和期望的动态性能，控制律采用自适应模糊方法缩短了调节时间、减小了控制变量抖振程度，使其既具有对系统参数大范围变化的强鲁棒性、对恶劣飞行环境的自适应能力，又对工作状态突发大偏离时具有快速应对能力，保证飞行任务的完成。同时，在侧向轨迹控制方面，利用割线法提出一种快速收敛的倾侧角反向时机在线规划方法，提高侧向制导的精度。

1 RLV 动力学建模

考虑地球为旋转圆球时，RLV 在航迹坐标系中无动力滑翔的无量纲质心运动方程［6］为

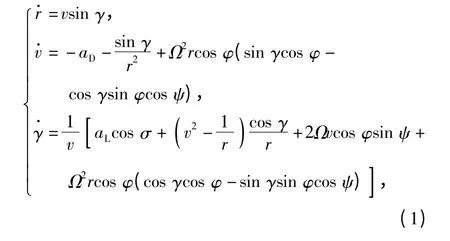
式中:r、v、s、Ω 分别为无量纲地心距、速度、航程和地球自转角速度;γ、ψ、λ、φ 分别为航迹角、航向角、纬度和经度;aL、aD分别为升、阻力加速度，均是控制变量攻角α 的函数;σ 为控制变量倾侧角。(1)式与(2)式分别为RLV 的纵向及侧向运动方程，(3)式为航程表达式。

2 基于模糊滑模变结构的跟踪控制

考虑如下一般形式的非线性时变系统:

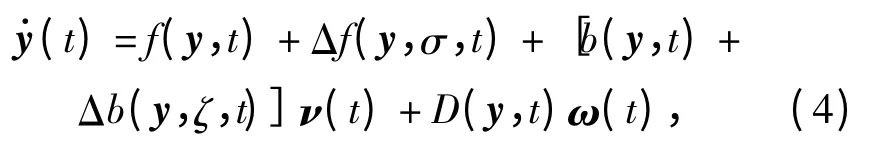
式中:y=［y1，y2，…，yn］T∈Rn为系统状态变量;ν=［ν1，ν2，…，νm］T∈Rm为控制量;σ(t)、ζ(t)分别为引起系统参数和输入不确定性变化的因素;ω(t)为不确定性扰动向量。

对(4)式在标称值附近进行小扰动线性化，得

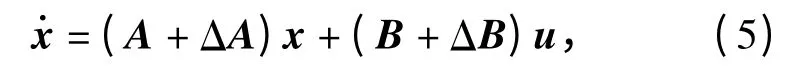
式中:x=y-y*，u=ν-ν*，分别为被控对象和控制输入实际真值与标称值之间的差异;ΔA、ΔB 为不确定性矩阵;A、B 分别为小扰动线性化得到的系统矩阵和控制矩阵。

变结构控制最突出的优点就是系统的滑模运动对不确定性具有很强的鲁棒性［7］。但是，有些时候，不确定性不在控制矩阵B 所张成的空间里，不能直接通过控制量u 的设计来抵消其影响。这时，控制器本身无法克服系统中的不确定性，但是通过合理地设计滑模面，可使系统的滑模运动具有较强的鲁棒性和所期望的动态性能［8］。

为了便于推导设计，作如下假设:

假设1 (A，B)可控，rank(B，ΔB)=rankB =m.

于是，存在非奇异线性变换x =Mz(M 为变换矩阵)，使得(5)式等效变换为

式中:z1∈Rn-m;z2∈Rm;B2为m×m 可逆方阵。

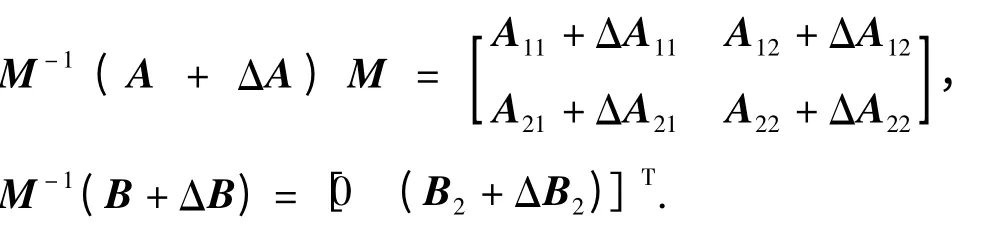
取切换函数为

式中:C∈Rm×n为待定矩阵。

根据上述线性变换有

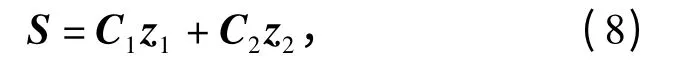
式中:CM=［C1C2］.

假设2 假设存在常数矩阵D1、D2、E1、E2和满足F1TF1≤I 与F2TF2≤I 的不确定矩阵F1、F2，使得ΔA11=D1F1E1，ΔA12=D2F2E2.

假设3 假设存在常数λ1、λ2、ξ，使得‖ΔA21‖≤λ1，‖ΔA22‖≤λ2，‖ΔB2‖≤ξ，这就意味着ΔA21、ΔA22和ΔB2有范数界。只要有满足条件的参数存在，即可构造出严格对角占优且非对角元素都为负的矩阵，使得＜0.

2.1 滑模面的设计

在滑动模态S=0 下，由(8)式有:

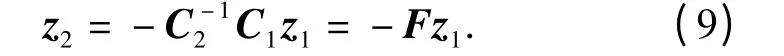
可以选择C2=Im，C1=F，则

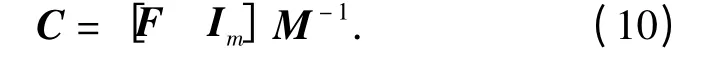
于是，变换后的子系统为

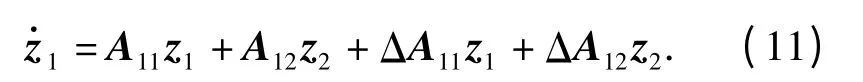
文献［8］证明了对于不确定系统(6)式，当ΔA11和ΔA12满足假设2 时，如果选择由(8)式和(10)式构成的切换函数，那么:

1)当S=0 时，所对应的等效系统是渐进稳定的。

2)当‖S‖≤σ 时，所对应的等效系统是一致终结有界的。

这样就保证了切换函数(7)式可以使原系统在S=0 时渐进稳定，在‖S‖≤σ 时一致终结有界。

原系统(5)式的滑动模可视为由(11)式描述且具有反馈(9)式的m 维子系统，因此选择合适的F可使滑动方程具有良好的动态特性。

这里采用最优化方法进行设计。

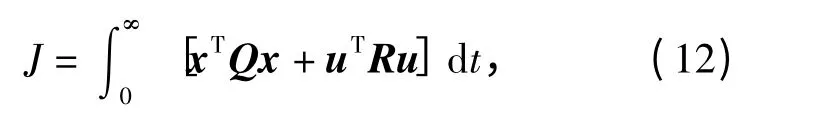
式中:Q 为误差成分加权矩阵;R 为控制分量加权矩阵。

由于在滑动模动态优化问题中，滑动模的运动与控制量无关，取R =0，则在等效系统的坐标下，(12)式可写成

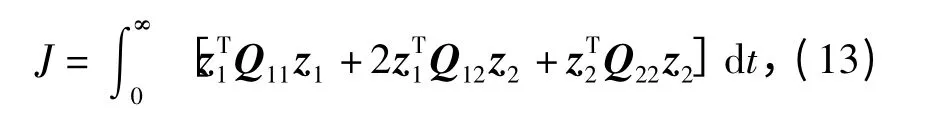
为了将最优滑动模设计问题写成二次性能指标下的一般形式，引入新的变量

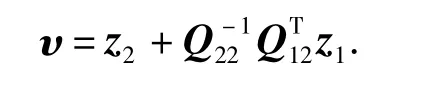
则性能指标(13)改写为

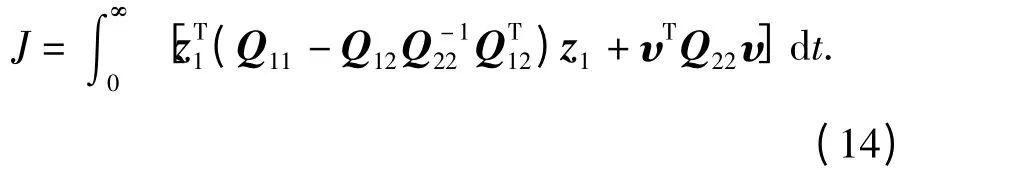
相应的滑动模方程为

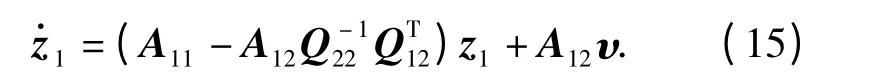
由最优控制理论，在滑动模方程(15)式中，作为控制作用的向量υ，其最优选择为

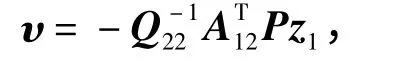
式中:P 是下列Riccati 方程的唯一解。

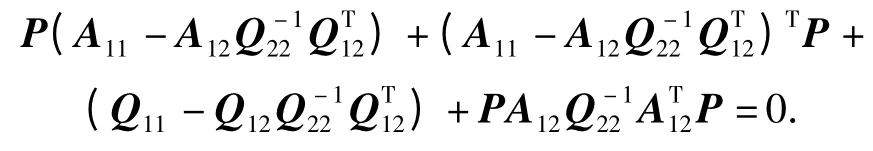
则有

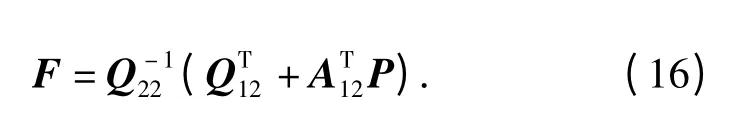
由于系统滑动时z2可以由z1线性表示出，因此只要z1趋于0，则z2也以同样衰减率趋于0. 这样即可保证滑动模态的渐进稳定性，使滑模运动具有较强的鲁棒性。

2.2 变结构控制律的设计

选择带边界层的指数趋近律:

式中:ε= diag(ε1，ε2，…，εm)，εi＞0;k = diag(k1，k2，…，km)，ki＞0;Θ=diag(θ1，θ2，…，θm)，θi＞0.

将(5)式、(7)式代入(17)式得变结构控制律:

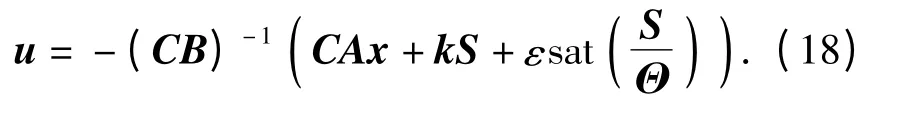
若系统满足假设3，切换函数由(7)式、(10)式构成，那么所设计的变结构控制律(18)式可使ST＜0 恒成立［8-9］，保证滑模面的存在及可达性，并可在不等式约束k ＜C2(ΔA21z1+ ΔA22z2+ ΔB2u)≤λ1z1+λ2z2+ξu 范围内通过增大k 值来缩短调节时间。

由于不确定性干扰存在时，会引起系统状态变量的值发生变化，而滑模面S 是关于状态变量的函数，那么，不确定性干扰的大小可以间接地通过S的取值来估计［10］。因此，与现有控制律设计不同，本文在文献［9］的基础上，设计二维模糊自适应控制器，根据滑模面Si与其导数的大小实时地调整趋近律参数εi，控制器原理如图1所示。

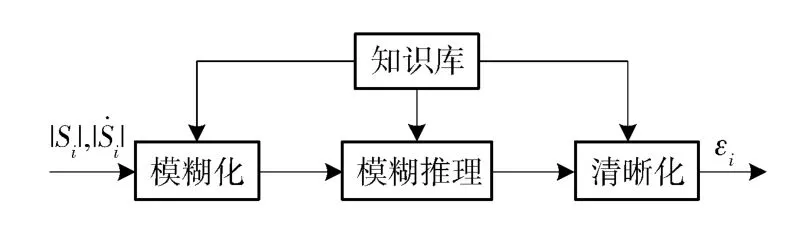
图1 模糊控制器原理图Fig.1 Fuzzy control diagram

定义输入|Si|和||的论域为［0，θi］，输出εi的论域为［0，1］，其中θi为待定参数。

对输入、输出空间进行同样的均匀模糊分割。设控制器输入|Si|、||及输出εi的模糊集分别为

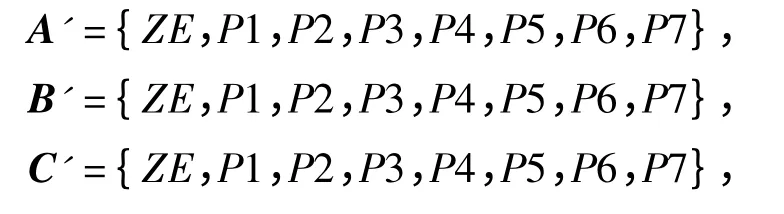
式中:ZE ～P7 分别代表0～7 档。

隶属函数μC'(εij)选择高斯隶属函数，形式为

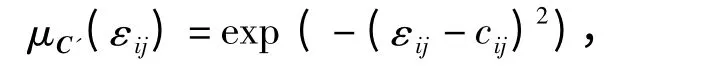
式中:cij=

由于当系统状态远离滑模面时，需要较大的控制作用加快趋近速度，将系统轨迹拉至滑模面;当系统状态靠近滑模面时，需要略小的控制作用将系统轨迹收敛至原点，并削弱系统抖振现象。因此，远离滑模面时控制器输出主要由|Si|决定，靠近滑模面时主要由||决定，并分别随|Si|和||的减小逐渐减小。建立控制规则表如表1所示。

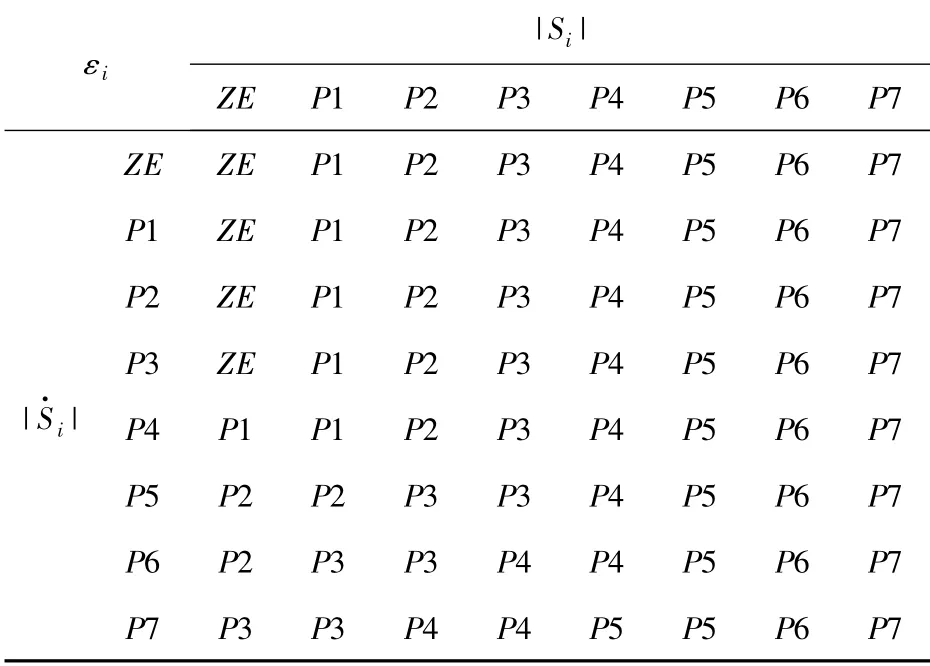
表1 控制规则表Tab.1 Fuzzy control rules

根据自适应理论，θi由(19)式进行在线调节。

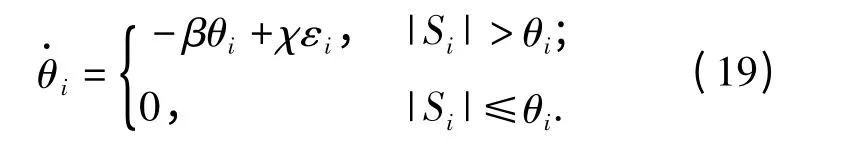
式中:β、χ 为滤波参数，可根据实际情况进行选取，本文选取β=5，χ=2.

模糊推理采用Mamdani 最大-最小规则，模糊判决方法采用加权平均法，利用(20)式得到实际控制量εi.

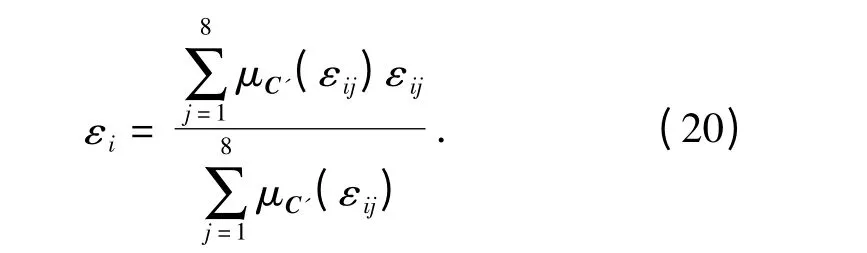
这样，得到模糊滑模变结构控制器的控制面如图2所示。

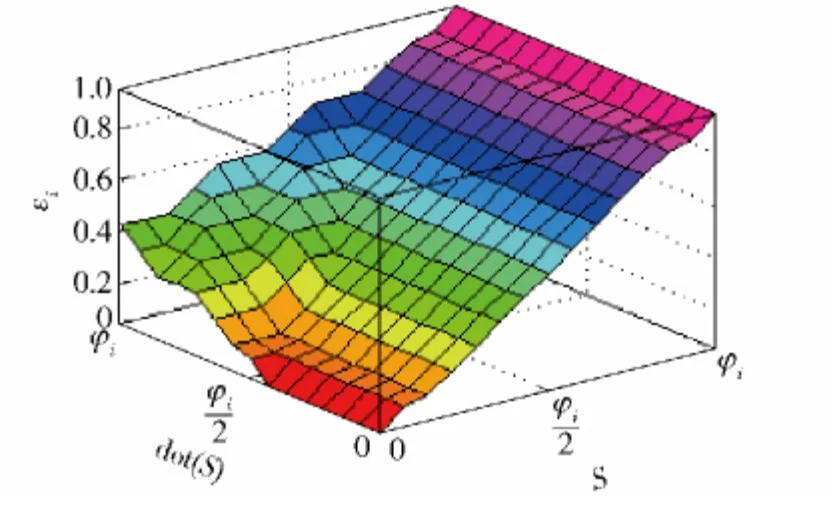
图2 模糊控制面Fig.2 Fuzzy control surface

3 基于割线法的倾侧角反向时机在线规划

倾侧角反向时机在线规划方法是在采用航向角跟踪视线角方法的基础上，通过一维快速迭代，搜索该剖面倾侧角最优反向点srev，使得飞行器达到指定航程时，航向角偏差在允许范围内。

设RLV 当前位置点经度、纬度(φn，λn)相对目标点经度、纬度(φf，λf)的视线角为ψp，其计算公式为

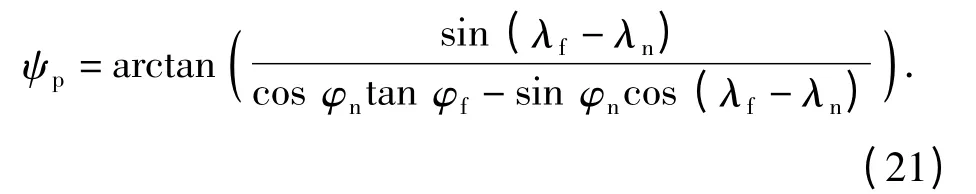
定义视线角误差Δψ 为当前航向角与视线角之差，即

sψ描述了实际轨迹距离目标点的精度，如图3所示，srev的取值决定了倾侧角的反向点，进而决定了到达目标点的侧向偏差。

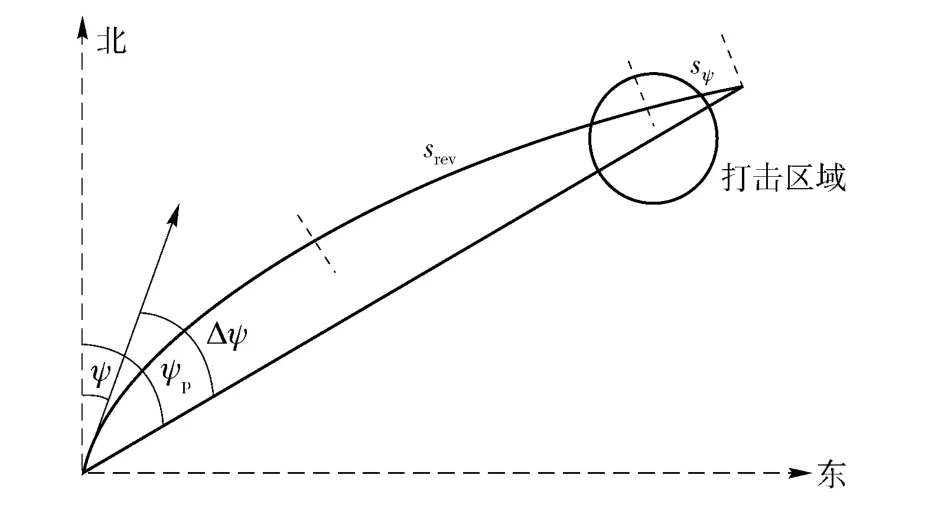
图3 倾侧角反向几何关系示意图Fig.3 Geometry for determining bank reversal point

本文采用割线法求解srev的取值。其迭代计算公式为

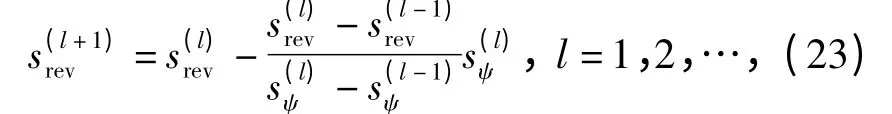
计算流程如图4所示，将前两步srev取值代入(23)式得到当前反正点srev，积分(1)式及(2)式.当s ＞srev时，倾侧角σ 取其负值，当终点sψ满足精度要求时仿真结束。

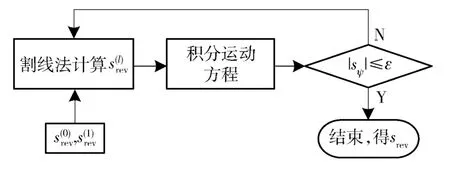
图4 倾侧角反向点在线规划流程图Fig.4 Flowchart of algorithm

4 研究实例

4.1 参考轨迹的设计

一般情况下，参考轨迹是在再入走廊中利用轨迹优化的方法离线设计的［11］，但考虑到制导系统的实时性要求，本文将再入过程中的弹道约束转换为控制变量约束，采用割线法完成对倾侧角的搜索，得到名义控制变量α*、σ*，实现3 自由度轨迹的在线生成［6］。

4.2 参考轨迹的跟踪

利用飞行器的纵向动态特性只与倾侧角σ 大小有关的特点，本文利用模糊滑模变结构控制方法，通过调节攻角α 与倾侧角大小|σ|完成对纵向平面的跟踪。通过在线规划倾侧角反向时机改变倾侧角σ 的符号将航向角误差控制在一定范围内。

4.2.1 纵向轨迹跟踪

对(1)式、(2)式同时进行积分可得当前实际飞行状态(r，v，γ)，在纵向控制律设计方面，由于纵、侧向耦合较小，为了在纵向参考轨迹(r*，v*，γ*)附近进行小扰动线性化，略去地球旋转项，取状态变量x=［δr，δv，δγ］T，控制变量u=［δ|σ|，δα］T，有

对小扰动线性化后的系统，令M=I3，z1=x1，z2=

运用Bryson 法则，得到以下关系:

将(10)式、(16)式代入(7)式得到具有良好动态特性的滑模面，增强系统鲁棒性，将(7)式、(20)式代入(18)式得到最终滑模控制律u，保证在较短时间内到达滑模面并能有效地削弱系统的抖振。

4.2.2 侧向轨迹跟踪

航天飞机的侧向制导采用的是边界走廊约束法［12］，但是这种方法:一方面由于倾侧角的反向是一个动态过程，不可能瞬间完成，因此倾侧角的反向次数必然受到限制，侧向走廊范围不能过窄;另一方面，若侧向走廊过宽虽能减小倾侧角反向次数，却增大了终端航向角偏差。

因此，本文在纵向跟踪控制的同时，利用(21)式、(22)式求出视线角误差Δψ，按图4在线搜索倾侧角反向点，利用(23)式经过较少的迭代次数计算得到满足条件的srev，完成倾侧角反向点的在线规划，其中迭代初值可利用文献［6］中的方法估计选取。

4.3 仿真结果分析

在某型RLV 模型上进行仿真，给定再入初始高度60 km，速度6 500 m/s，航迹角0°，航向角90°，经度0°，纬度0°;终端高度45 km，速度4 000 m/s，航迹角不大于1°，目标点为经度45°，纬度0°.

由于影响制导精度的因素主要是气动系数偏差和初始状态误差，且气动参数偏差以升力系数减小阻力系数增大为最恶劣，为了使控制方法具有普遍适用性，在模型参数中引入如下不确定性:初始状态偏差H*=H +5 km，v*=v +500 m/s，γ*=γ +1°;再入过程气动参数摄动C*L=CL(1 -20%)，C*D=CD(1 +20%).

分别采用最优控制方法与本文设计的模糊滑模变结构方法进行仿真，跟踪曲线如图5所示，纵向跟踪结果如表2所示，其中ΔH、Δv、Δγ 分别表示终端高度误差、速度误差和航迹角误差，τ 表示误差收敛时间。

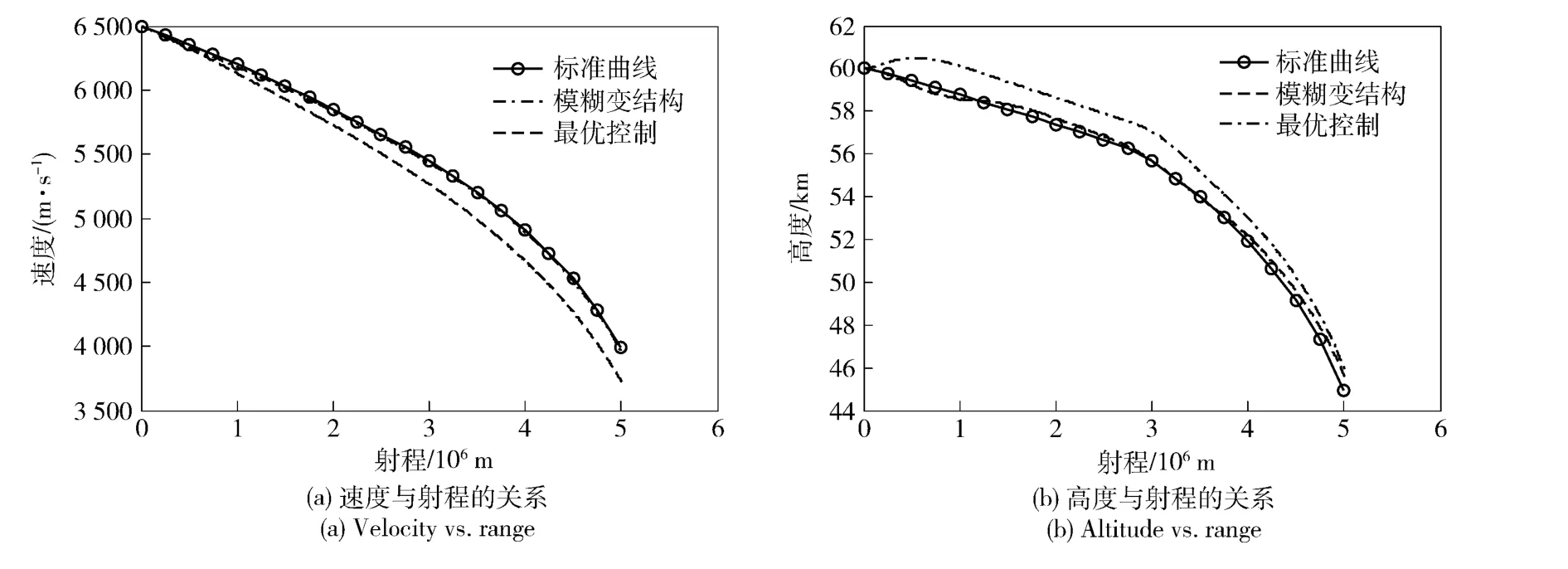
图5 状态变量对比曲线Fig.5 Comparison curves of state variables

表2 再入终端纵向性能比较Tab.2 Terminal error comparison

从表2中数据可以看出，与最优控制相比，纵向跟踪误差大大减小，尤其表现在对速度状态的跟踪上，由于阻力加速度发生较大的正向偏差，必然带来飞行器速度的迅速下降，即使采用最优控制方法，终端速度跟踪误差仍可达120.1 m/s，而采用模糊滑模变结构控制方法，速度跟踪误差不超过25 m/s，在很大程度上提高了制导精度。

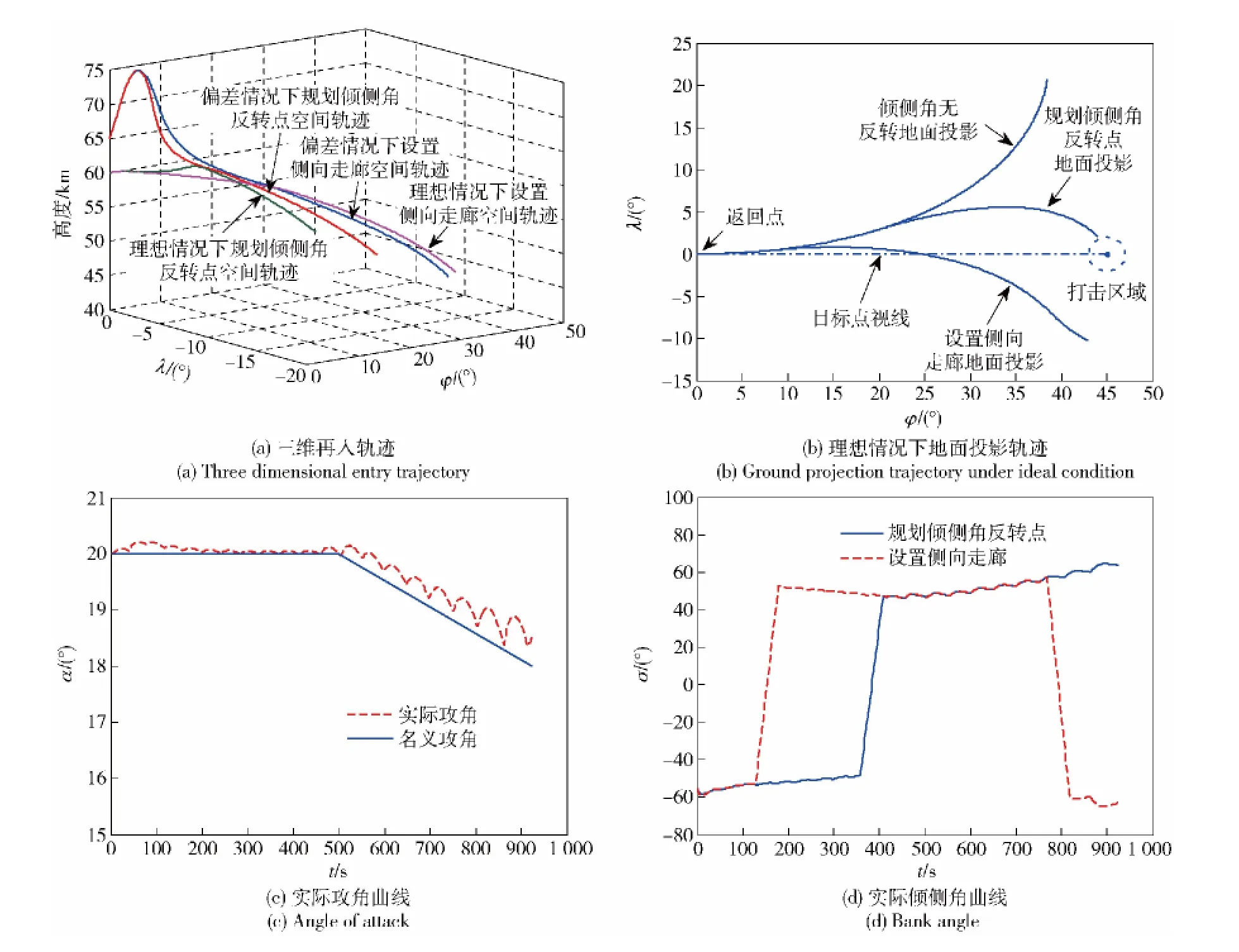
图6 再入轨迹与控制变量曲线Fig.6 Reentry trajectory and control variables

图6给出了在纵向跟踪采用模糊滑模变结构的情况下，横向控制采用边界走廊约束法与本文设计的在线规划倾侧角反向时机法得到的空间再入轨迹曲线、地面投影曲线以及控制量攻角与倾侧角的历程曲线。仿真结果表明在纵向跟踪方面，采用模糊自适应方法设计趋近律参数可以有效地将控制变量抖振频率控制在0.02 Hz 以下，且幅度不超过0.5°.在横向轨迹控制方面，采用传统的边界走廊约束法尽管进行了两次倾侧角反向，但返回轨迹仍有10°的纬度偏差，而采用本文设计的在线规划倾侧角反向时机的方法虽然仅进行一次倾侧角反向，但返回轨迹可到达目标区域中，经度、纬度偏差在2°以内，使落点精度得到大幅度提高，较好地满足了侧向制导要求。同时，在计算机(双核CPU，主频1.6 GHz，编译环境为Matlab7.0)完成上述仿真时间为8 ～9 s，迭代次数不超过10 次，能够进行在线求解。

5 结论

针对RLV 准平衡滑翔阶段特殊的飞行模式、恶劣的飞行环境以及不确定性较大的特点，在纵向平面提出一种具有强鲁棒性的模糊变结构跟踪控制方法，并在侧向平面进行倾侧角反向点的在线规划。仿真结果表明:

1)在存在较大初始状态偏差及剧烈气动参数摄动的情况下，通过优化设计滑模面，有效地提高了系统的鲁棒性，实现了对纵向参考轨迹的稳定跟踪。

2)通过采用模糊自适应方法对趋近律参数进行实时调节，有效地削弱了系统状态越过滑模面引起的抖振，将控制变量抖振频率控制在0.02 Hz 以下，幅值控制在0.5°以内。

3)在侧向轨迹控制方面，通过在线规划一次倾侧角反向时机，有效地解决了传统边界走廊约束法反向次数多并且落点误差大的缺点，使侧向制导精度有了大幅度提高。

References)

［1］尹佳杰，都延丽，陆宇平.近空间飞行器滑翔再入控制的研究方法与进展［J］.飞行力学，2013，31(6):203 -208.YIN Jia-jie，DU Yan-li，LU Yu-ping. Research methods and development of gliding reentry control for near space vehicles［J］.Flight Dynamics，2013，31(6):203 -208. (in Chinese)

［2］Dukeman G A. Profile-following entry guidance using linearquadratic regulatory theory［C］∥AIAA Guidance，Navigation，and Control Conference and Exhibit. Monterey，California:AIAA，2002.

［3］Zhou W Y，Tan S J，Chen H B. A simple reentry trajectory generation and tracking scheme for common aero vehicle［C］∥AIAA Guidance，Navigation，and Control Conference and Exhibit. Minneapolis:AIAA，2012.

［4］胡跃明. 非线性控制系统理论与应用［M］. 北京:国防工业出版社，2005:154 -175.HU Yue-ming. Theory and application of nonlinear control system［M］. Beijing:National Defense Industry Press，2005:154 -175.(in Chinese)

［5］张大元，雷虎民，吴玲，等.基于滑模变结构的弹道跟踪制导律设计［J］.系统工程与电子技术，2014，36(4):721 -727.ZHANG Da-yuan，LEI Hu-min，WU Ling，et al. A trajectory tracking guidance law based on sliding mode variable structure control［J］. Systems Engineering and Electronics. 2014，36 (4):721 -727.(in Chinese)

［6］Shen Z J. On-board three-dimensional constrained entry flight trajectory generation［J］. Dissertation Abstracts International，2002，63(8):3804.

［7］Yousef H，A，Hamdy M，Shafiq M. Adaptive fuzzy-based tracking control for a class of strict-feedback SISO nonlinear time-delay systems without backstepping［J］. International Journal of Unicertainty，Fuzziness and Knowledge-Based System，2012，20(3):339 -353.

［8］胡剑波. 一类非匹配不确定性系统的变结构控制［J］. 控制理论与应用，2002，19(1):105 -108.HU Jian-bo. Variable structure control for a class of systems with mismatched uncertainties［J］. Control Theory and Application，2002，19(1):105 -108. (in Chinese)

［9］周凤岐，王延，周军，等. 高超声速飞行器耦合系统变结构控制设计［J］. 宇航学报，2011，32(1):66 -71.ZHOU Feng-qi，WANG Yan，ZHOU Jun，et al. Design of variable structure controller for hypersonic coupled vehicle system［J］.Journal of Astronautics，2011，32(1):66 -71.(in Chinese)

［10］Ha Quang Thinh Ngo，Jin-Ho Shin，Won-Ho Kim. Fuzzy sliding mode control for a robot manipulator［J］. Artificial Life and Robotics. 2008，13(1):124 -128.

［11］Ping L. An alternative entry guidance scheme for the X-33［J］.American Institute of Aeronautics and Astronautics. 1998(8):189 -199.

［12］赵汉元.航天器再入制导方法综述［J］. 航天控制，1994(1):345 -348.ZHAO Han-yuan. A survey of guidance methods for spacecraft reentry［J］. Aerospace Control，1994(1):345 -348. (in Chinese)