海流能发电系统功率跟踪控制策略方法研究

毛昭勇，黄伟超，樊瑜

(西北工业大学 航海学院，陕西 西安710072)

0 引言

为了有效地解决能源危机和大气环境的污染问题，人们正在积极开发各种可再生的新能源来代替传统的能源发电。海流能由于具有可再生、绿色环保的性质，日益受到世界许多国家的重视。据估计，世界各大海洋中所有海流的总功率达50 亿kW 左右，因此，科学地、更大规模地利用海流能对维持经济的可持续发展具有重要和深远的意义。

考虑到海流能具有不规则的特点，本文主要针对一种可伸缩式垂直轴叶轮海流能发电系统，开展最大功率点跟踪控制策略研究，解决在海流动态变化过程中的最大能量捕获问题。目前，最大海流能捕获控制方法主要有最佳叶尖速比查表法、爬山搜索法、模糊控制和自适应控制法等，其中查表法要求有准确的海流速信号，但海底环境比较复杂，海流速难以准确测量;搜索法需要对转速进行连续试探性的调节，易产生转矩高频脉动，增加传动链的疲劳载荷;而模糊控制和自适应控制方法较为复杂，对控制器的设计要求较高［1］。因此，本文在研究过程中，根据海流能发电系统的运动方程和转矩特性，提出了一种基于2 阶滑模控制的最佳转矩控制策略。该方法只需测量叶轮转速，不需要测量海流流速，提高了系统的控制精度，并且控制器的设计相对简单，易于实现。最后通过仿真研究，结果表明模型分析方法和控制策略是合理可行的。

1 海流能发电系统运动特性分析

1.1 海流能发电系统结构模型

海流能发电系统根据自身轴线与海水流动方向的相对位置，可分为水平轴式和垂直轴式的海流能发电系统［2］。相比水平轴式海流能发电系统，垂直轴式海流能发电系统的叶轮轴线与来流方向垂直，可以捕获任何方向的海流能，效率较高，很适合小型化独立发电［3］。一般垂直轴式海流能发电系统在结构组成上主要由叶轮、增速齿轮箱、发电机、功率调节控制装置等组成(如图1所示)，其工作原理与风力发电机相似，叶轮在流体介质中受到水动力作用从而带动转轴转动，将流体动能转换成机械能，增速齿轮箱将低速大扭矩的机械能进行转换并传递至发电机，发电机将机械能转换成电能，同时对电能进行调节并输出至负载。

考虑到叶轮的一个旋转周期分为进程(顺流方向)和回程(迎流方向)两个过程，阻力型叶轮主要在进程产生驱动力矩，而在回程过程中产生阻碍叶轮旋转的力矩，减小该力矩可有效提高叶轮效率。为了减小叶轮回程阻力，本文提出了一种可伸缩式垂直轴式叶轮结构［4］(如图2所示)，主要由动力轴、偏心轴、导流罩、多根连杆和叶片组成。动力轴与导流罩同轴固定安装。偏心轴与动力轴轴线平行，二者轴线具有一定偏心距。偏心轴与动力轴通过同步带连接，保证两根轴具有相同的旋转速度。导流罩壁上有与叶片数目对应的矩形安装孔，连杆通过该安装孔伸出至导流罩外部，叶片通过连杆与偏心轴上的偏心圆盘连接，连杆两端均为铰接。工作原理为:叶轮在海流作用下，在进程时通过偏心轴上的偏心圆盘及连杆将叶片展开，产生驱动叶轮旋转的驱动力矩;在完全伸出之后，叶片又被偏心圆盘及连杆拉回至导流罩，减小叶轮回程时的阻力。

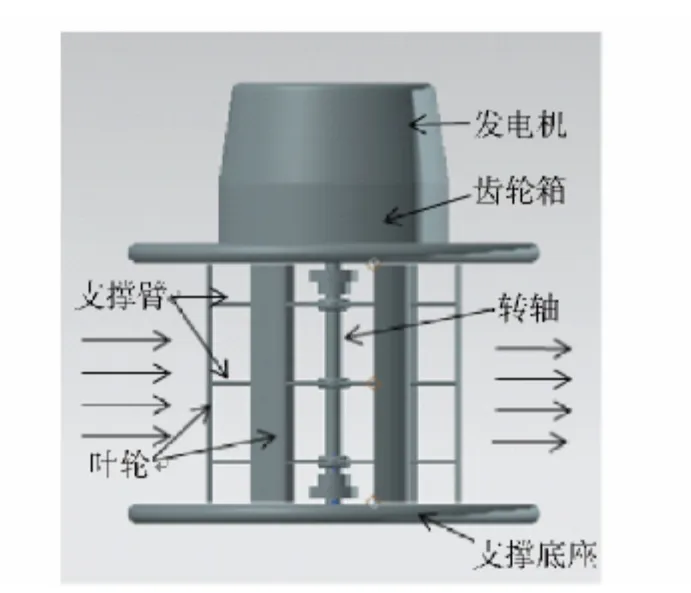
图1 垂直轴式海流发电系统Fig.1 The vertical axis type current power generation system

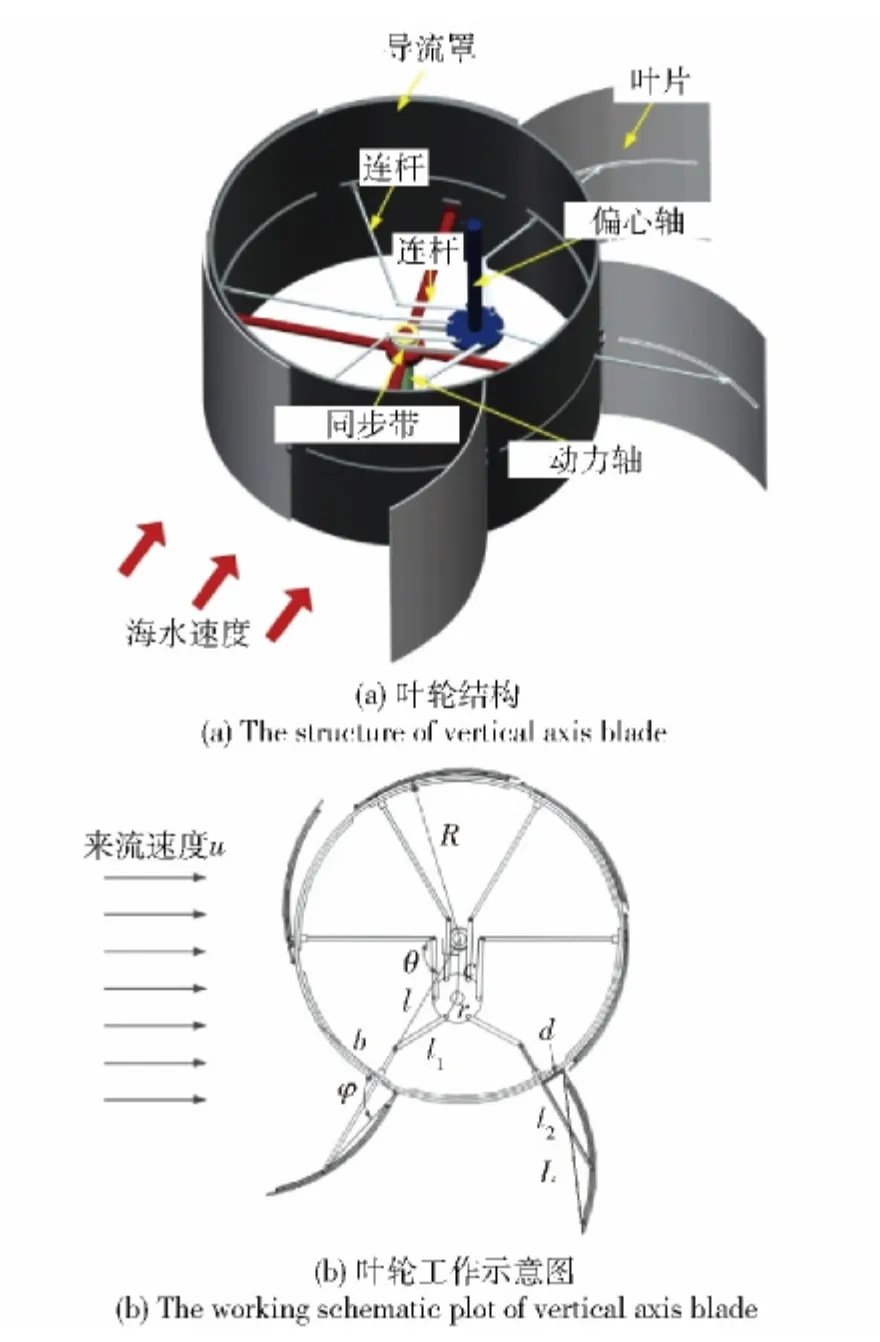
图2 可伸缩式垂直轴叶轮结构及工作示意图Fig.2 The structure and working schematic plot of extensible vertical axis blade

表1给出了叶轮主要几何参数。

表1 叶轮主要几何参数Tab.1 Main geometric parameters of blade

1.2 发电系统运动特性

根据Betz 理论，垂直轴式海流能发电系统从海水中捕获的功率［5］为

式中:Pa为叶轮捕获功率;ρ 为海水密度;S 为叶轮叶片的扫截面积;CP为海流能利用系数;v 为海流速;β 为桨距角;λ 代表叶尖速比;ωr为叶轮旋转的角速度;H 为叶轮的高度。随着叶轮旋转，迎流方向的有效叶片长度等于叶片弦长，又叶片弦长等于导流罩半径，故取R 为叶轮等效半径。

从海水中捕获的功率也可表示为

式中:Tr为叶轮输出转矩。

由(1)式、(2)式和(4)式得

海流能利用系数CP是关于叶尖速比λ 和桨距角β 的非线性函数，其大小表征了海流能发电系统吸收海流能的能力。当桨距角恒定时，海流能发电系统只能在某一确定的叶尖速比λ 下到达利用系数最大值CPmax，此时的叶尖速比称为最佳叶尖速比λopt. 设海流能发电系统的输出转矩参考值为

式中:转矩系数kopt为叶尖速比最佳时的常数。因此，对于任意转速、流速时，系统通过反馈控制，进入稳定状态后，叶轮实际输出转矩才与叶轮输出转矩参考值Topt相等。

根据本文所给出的海流能发电系统结构模型，桨距为定桨距，桨距角β=0°，根据(5)式可知，转矩系数kopt可表示为

为了研究海流能发电系统的运动特性，必须要获得叶轮海流能利用系数CP与叶尖速比λ 的函数。为此，本文基于所建立的叶轮结构模型，利用流体动力分析软件Fluent 对叶轮进行了二维计算流体动力学(CFD)数值计算，获得了不同叶尖速比λ 下的海流能利用系数CP(如表2所示)。

表2 不同叶尖速比下的海流能利用系数Tab.2 Utilization coefficients under different tip speed ratios

为了实现叶轮的最大功率跟踪，根据表2的数据经过多次最小二乘拟合，通过选用拟合误差最小，得到了海流能利用系数CP与叶尖速比λ 的关系函数，拟合曲线如图3所示。

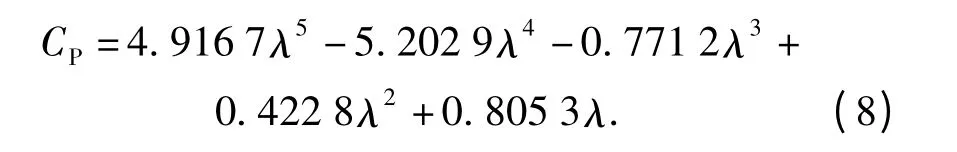
图3 叶尖速比与海流能利用系数关系曲线Fig.3 Tip speed ratio vs. current utilization coefficient

从图3可以看出，叶轮的最大功率利用系数为0.259 5，此时所对应的叶尖速比为0.4.

2 最大功率跟踪控制策略建模分析

2.1 系统模型简化

根据本文所给出的海流能发电系统结构模型，其传动系统经过简化后，其2 阶模型如图4所示。

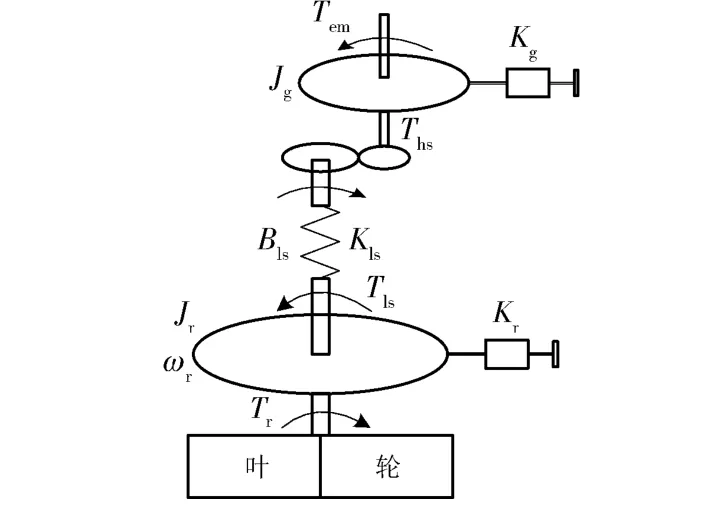
图4 发电系统2 阶模型Fig.4 The second order model of power system

图4中:Jr为叶轮转子转动惯量;Tls是低速轴反转矩;Kr为叶轮转子外部阻尼;Bls为低速轴等效刚度;Kls为低速轴等效阻尼;Ths为高速轴转矩;ωg为发电机角速度;Jg为发电机转动惯量;Kg为发电机转子外部阻尼;Tem为发电机电磁转矩。

结合转子动力学和发电机惯性的特点，2 阶模型可以等效为如下微分方程:

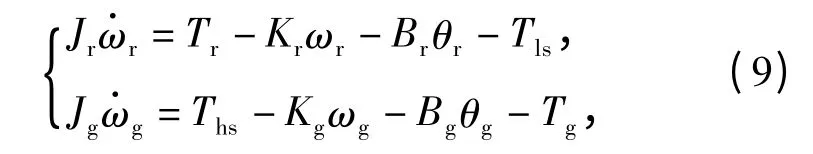
式中:Br、θr、Bg、θg分别为叶轮和发电机转子的等效刚度和转子角度;

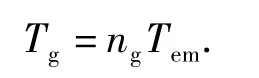
增速齿轮箱的增速比为

因此，(9)式可以等效为

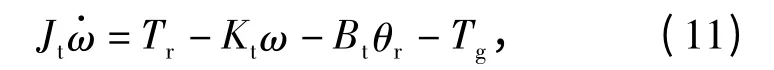
式中:Jt=Jr+n2gJg;Kt=Kr+n2gKg;Bt=Br+n2gBg.

由于外部刚度Bt很小，可以忽略。因此，将使用以下简化模型用于控制目的:

2.2 最大功率跟踪控制系统设计

本文采用最佳转矩的控制策略(如图5所示)，通过计算实时转速所对应的参考转矩作为控制发电机电磁转矩的给定值，通过反馈调节，确保叶轮输出转矩Tr收敛于Topt，叶轮的转速自动跟踪并平衡在当前海流速下的最佳转速点，实现最大功率跟踪控制。

同时，通过对海流能发电系统运动模型的分析可知，海流能发电系统具有非线性、时变、非稳定的特点，因此，本文采用非线性控制方法。滑模控制是一种非常有效的非线性控制方法，具有结构简单、对外界干扰和参数摄动具有很强的鲁棒性等许多优点。然而，滑模控制由于采用离散控制律，因此需要解决抖颤问题，通常低通滤波器被用于减小抖振问题，却带来了延时，本文采用高阶滑模对系统进行状态观测控制，从而减小了由于系统高频离散控制带来的抖颤，对于海流能发电系统最大功率跟踪，有很好的控制效果［6］。

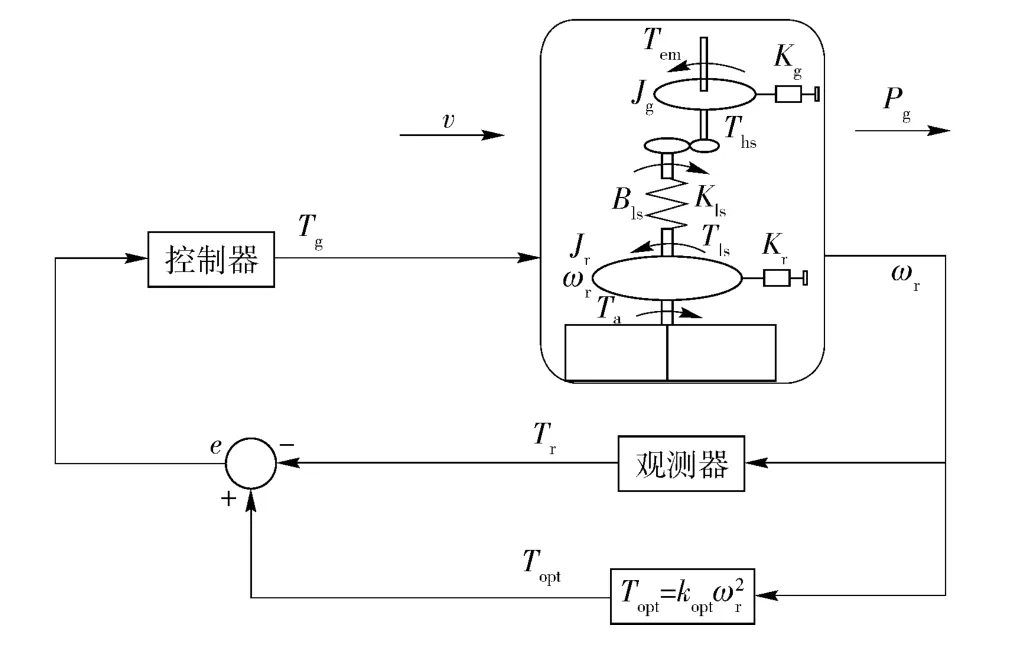
图5 控制策略Fig.5 Control strategy

根据本文采用的最佳转矩控制策略思想，使叶轮的输出转矩跟踪系统参考转矩Topt，因此设计跟踪误差为

其2 阶导数为

式中:A=2koptωr/Jt;B=2koptωr/Jt(Tr-Ktωr)-

Super-Twisting 算法是一种常用的2 阶滑模控制的算法，是针对系统滑模变量的相关度为1 提出的，该算法完全消除了系统抖动。由Super-Twisting算法得滑模控制律［6-7］为

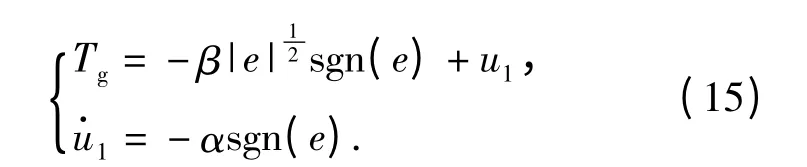
保证有限时间内收敛于滑模面原点的充分条件是

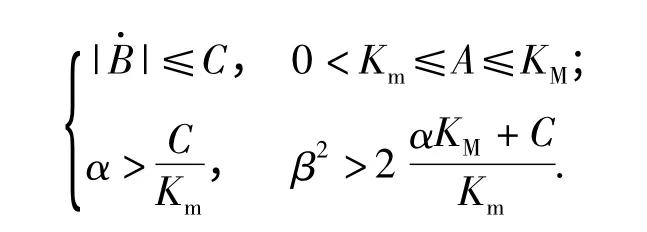
式中:α、β、C、Km、KM均为常数。

当α，β 满足上述条件时，存在一个时间点使得Tr=Topt，所以本文通过控制叶轮的输出转矩与系统参考转矩Topt的误差来调叶轮转速，进而实现最大功率跟踪。

3 系统仿真分析

为了验证本文模型的可行性，基于Matlab/Simulink 仿真软件［8］，根据最佳转矩的控制策略，建立的最大功率跟踪控制仿真模型(如图6所示)包括叶轮模块、MPPT 模块和2 阶滑模控制模块。仿真时，海流驱动叶轮旋转，首先测量叶轮转速，然后基于叶轮实际转速，根据最大功率模块计算叶轮实际转速对应的参考转矩作为控制海流能发电机电磁转矩的参考值，最后根据2 阶滑模控制器不断反馈调节，从而控制叶轮的转速自动追踪并平衡在叶轮的最佳转速，即实现海流能发电最大功率追踪控制。

图6 系统仿真模型Fig.6 Simulation model of system

在仿真过程中，控制算法参数:α =1 000、β =100、kopt=259，叶轮初始转速为0.5 rad/s，并采用文献［9］提供的海流流速信号(如图7所示，平均海流速为2 m/s)作为仿真模型的输入，对不同海流速下的功率跟踪情况进行了仿真分析，仿真结果如图8～图10 所示。

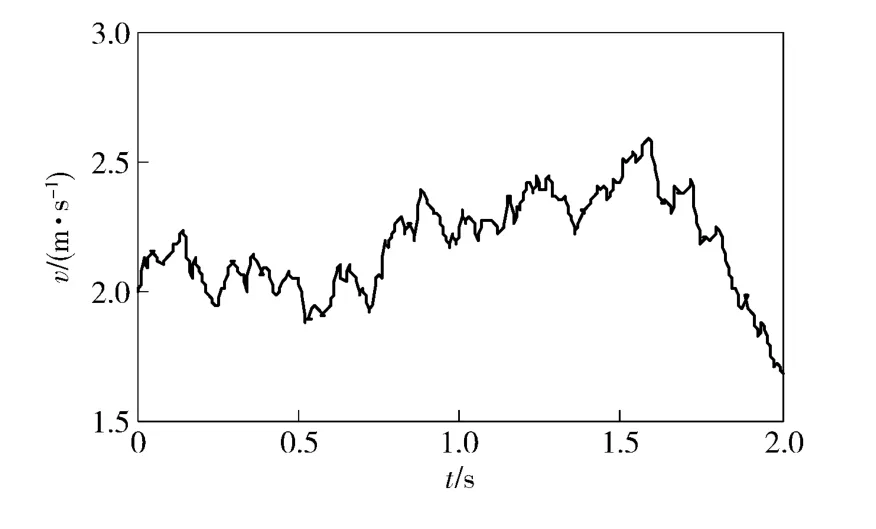
图7 海流速仿真曲线Fig.7 Curve of velocity

图8 海流能利用系数CP 曲线Fig.8 curve of CP

从图8可以看出，当流速在2 m/s 左右变化时，叶轮的功率系数基本上维持在最大值CPmax=0.259 5 附近，实现了最大功率点的跟踪。从图9和图10 可知，由于叶轮初始转速较低，通过反馈调节，叶轮转速快速增大，导致系统理想功率输出较大，随着系统进入稳态后，叶轮的实际输出功率可以很好地跟踪系统理论最大输出功率。

4 结论

1)本文针对一种可伸缩式垂直轴叶轮海流能发电系统，建立了发电系统的运动方程。

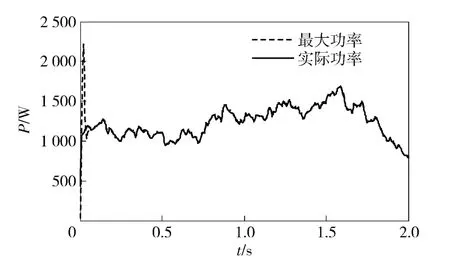
图9 功率曲线Fig.9 Curves of power

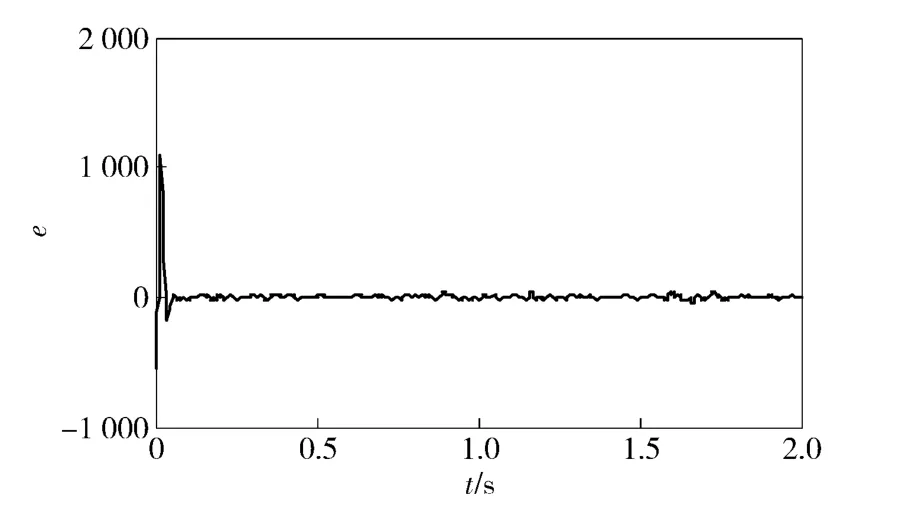
图10 功率误差曲线Fig.10 Curve of power error

2)本文根据发电系统的运动方程和转矩特性，提出了一种基于2 阶滑模控制的最佳转矩控制策略，将叶轮模型输出的转矩作为转矩环的反馈信号。仿真结果表明，本文所设计的功率调节装置和控制系统能使海流能发电系统动态地跟踪最大功率点，解决了在海流动态变化过程中的最大能量捕获问题。

3)仿真结果验证了本文提出的最大功率跟踪控制策略方法，具有良好动态特性和控制效果，对下一步实物样机设计和改进具有实际指导意义。

References)

［1］赵佩宏，李建林，鄂春良. 变速风力机的最大风能捕获控制策略研究［J］.电气传动，2009，39(6):3 -6.ZHAO Pei-hong，LI Jian-lin，E Chun-liang. Research on maximum power capture control strategy of variable wind turbine［J］.Electric Drive，2009，39(6):3 -6.(in Chinese)

［2］Myers L，Bahaj A. Experimental analysis of the flow field around horizontal axis tidal turbines by use of scale mesh disk rotor simulators［J］. Ocean Engineering，2010，37(2/3):218 -227.

［3］Yang B，Lawn C. Fluid dynamic performance of a vertical axis turbine for tidal currents［J］.Renewable Energy，2011，36(12):3355 -3366.

［4］Tian W L，Song B W，Mao Z Y，et al. Design of a novel vertical axis water turbine with retractable arc-type blades ［J］. Marine Technology Society Journal，2013，47(4):94 -100.

［5］马舜，李伟，刘宏伟，等. 海流能发电系统的最大功率跟踪控制研究［J］. 太阳能学报，2011，32(4):577 -582.MA Shun，LI Wei，LIU Hong-wei，et al. Study on maximum power tracking control for marine current energy conversion system［J］.Acta Energiae Solaris Sinica，2011，32(4):577 -582. (in Chinese)

［6］皇甫宜耿，刘卫国，马瑞卿. 基于二阶滑模观测器的永磁同步电动机伺服控制［J］. 微特电机，2008(11):32 -34.HUANGFU Yi-geng，LIU Wei-guo，MA Rui-qing. Second order sliding mode observer design for PMSM servo control［J］. Small and Special Electrical Machines，2008(11):32-34.(in Chinese)

［7］Beltran B，Ahmed-Ali T，Benbouzid M. High-order sliding-mode control of variable-speed wind turbines［J］. Industrial Electronics，2009，56(9):3314 -3321.

［8］刘金琨. 滑模变结构控制MATLAB 仿真［M］. 北京:清华大学出版社，2005.LIU Jin-kun. MATLAB simulation for sliding mode control［M］.Beijing:Tsinghua University Press，2005.(in Chinese)

［9］Payne G S，Kiprakis A E，Ehsan M，et al. Efficiency and dynamic performance of digital displacement TM hydraulic transmission in tidal current energy converters［J］. Journal of Power and Energy，2007，221(2):207 - 218.