输送机驱动装置机架的动力学分析与改进

安晓卫，刘 秦

(沈阳理工大学 机械工程学院，辽宁 沈阳 110159)

输送机驱动装置机架的动力学分析与改进

安晓卫，刘 秦

(沈阳理工大学 机械工程学院，辽宁 沈阳 110159)

采用参数化建模方法建立带式输送机驱动装置机架的有限元模型，对机架进行固有特性计算及强迫振动分析，计算出机架在工作时的振幅，通过对振幅曲线的分析，确定液力耦合器与机架的连接处为振动过大的位置，据此对机架结构进行改进设计。

机架；有限元；动力学仿真；结构改进

在带式输送机驱动装置的设计过程中，机架的设计仍采用静态计算和经验选用相结合的方式，在前期设计阶段由于缺乏试验模型，因此不能取得足够的实际经验以避免设计中潜在的缺陷，有关缺陷往往只在带式输送机投入使用一段时间后才能暴露出来。机架的一些问题直接影响驱动装置的稳定运行，甚至是安全问题，所以产品往往不得不返回到构造设计阶段以进行必要的修改，这样的设计过程效率低，费用高。文献[1]对某上机架进行了结构分析，确定了上机架的最大应力、变形值及位置,对其结构尺寸参数进行分析，在保证振动和力学性能的条件下，通过合理的尺寸优化降低了机架的重量。文献[2]对电机机架进行了模态分析和谐响应分析，直观显示了机架在电机运行时的工作状态，通过对机架结构尺寸的优化来减少材料成本。

某大型带式输送机在启动过程中，其振动幅度大于安全工作范围的一倍，本文用有限元方法对该机架进行动力学分析，确定机架振动过大的位置；在此基础之上，对机架结构进行改进设计。

1 驱动装置机架的有限元模型

驱动装置机架结构长4335mm，宽1030mm，高600mm；结构主要由侧板、上下横板、吊耳、角钢和挡板组成；材料为Q235。根据经验，机械结构阻尼通常很小，故取模态阻尼。

整个机架的侧板和上下横板是主要承重件，由于这些部件的结构特点采用板单元进行模拟(如图1所示)，应用有限元的变厚度板进行处理。减速器、电机、液力耦合器、制动器与机架为螺栓连接；机架的角钢、铆钉、吊耳和工艺小孔等对整个机架结构的强度和刚度影响很小，因此在建模时将这些忽略不计。由于电机、减速器等设备的刚度比机架大得多，故用集中质量单元模拟电机、液力耦合器、制动器和减速器。将质量单元作为主节点，机架螺栓处的节点为从属节点，将主节点与从属节点之间建立刚性连接(如图2所示)，通过刚性耦合的方法将电机和耦合器产生的激励传递到机上[3]。由于实际机架和地面用普通螺栓连接，所以机架底面完全固定。

图1 驱动装置机架的有限元模型

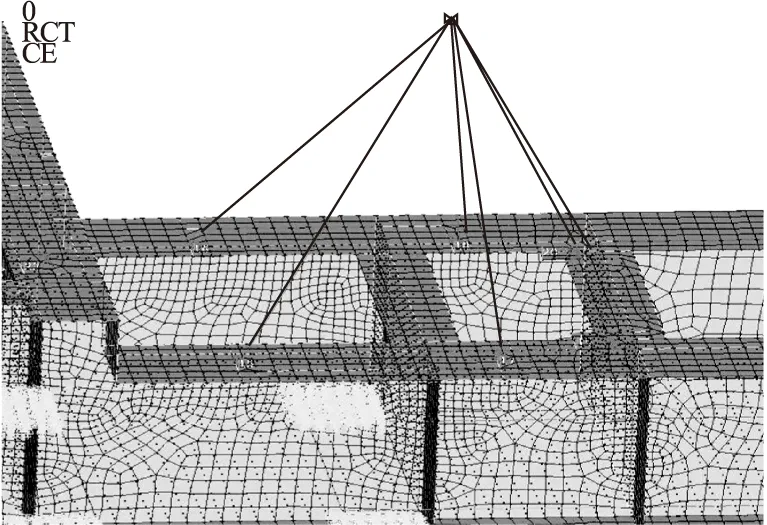
图2 耦合器支座处的刚性连接

2 机架的固有特性分析

分别计算出机架结构的前10阶固有频率和振型，第1阶至第10阶固有频率和振动形态如表1所示。机架第一阶固有频率为59.9Hz，而电机激励频率为26Hz，频率相差2.3倍，因而机架工作稳定，不会发生共振。1～5阶的振型如图3～6所示。

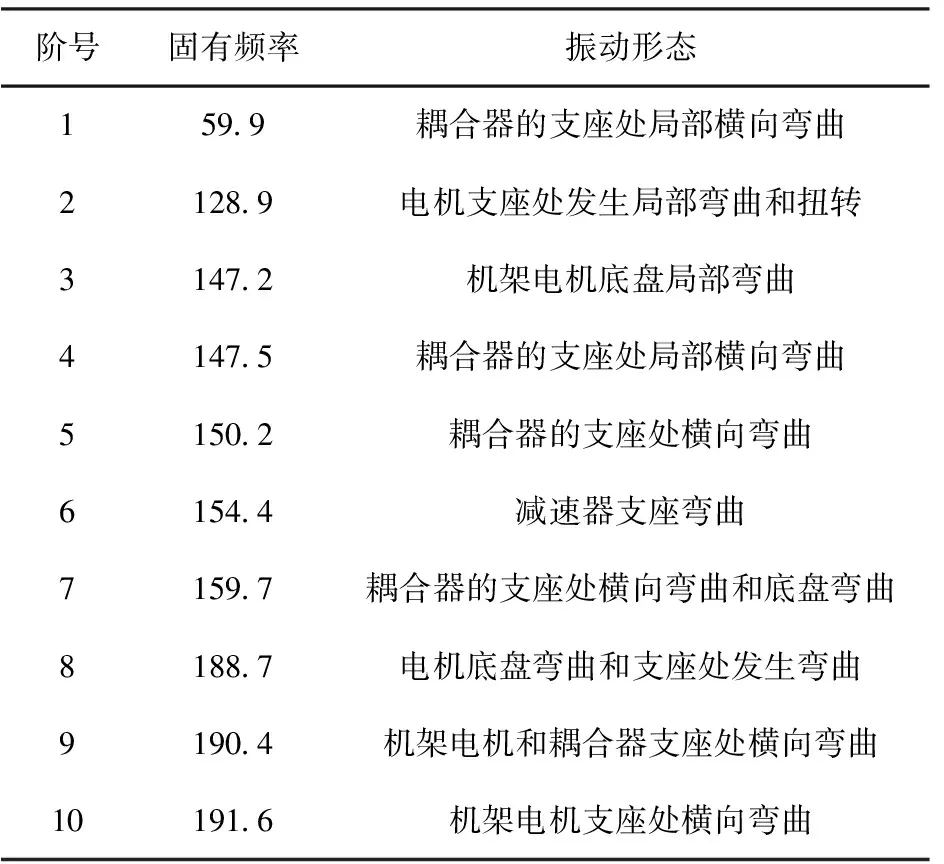
表1 机架固有频率 Hz

图3 第1阶振型

图4 第2阶振型

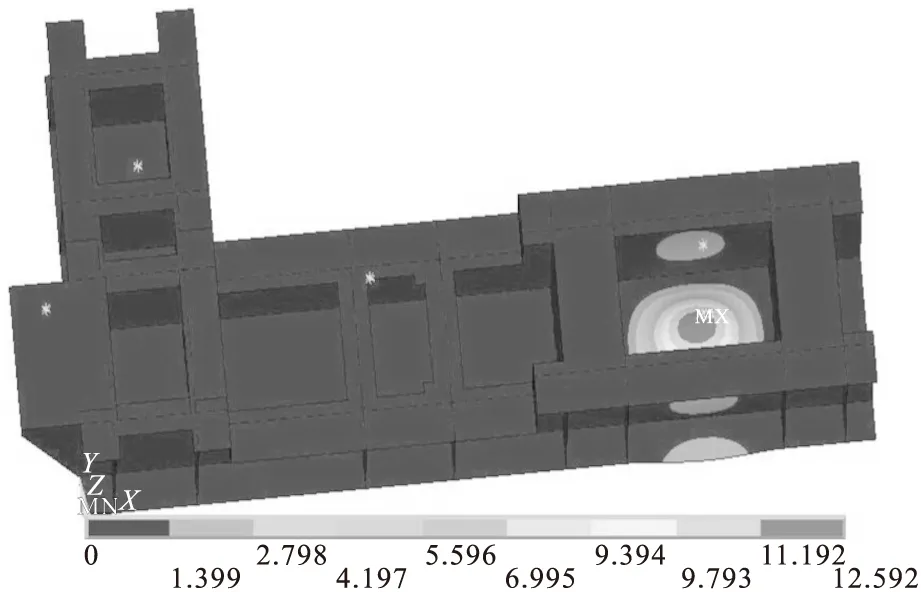
图5 第3阶振型

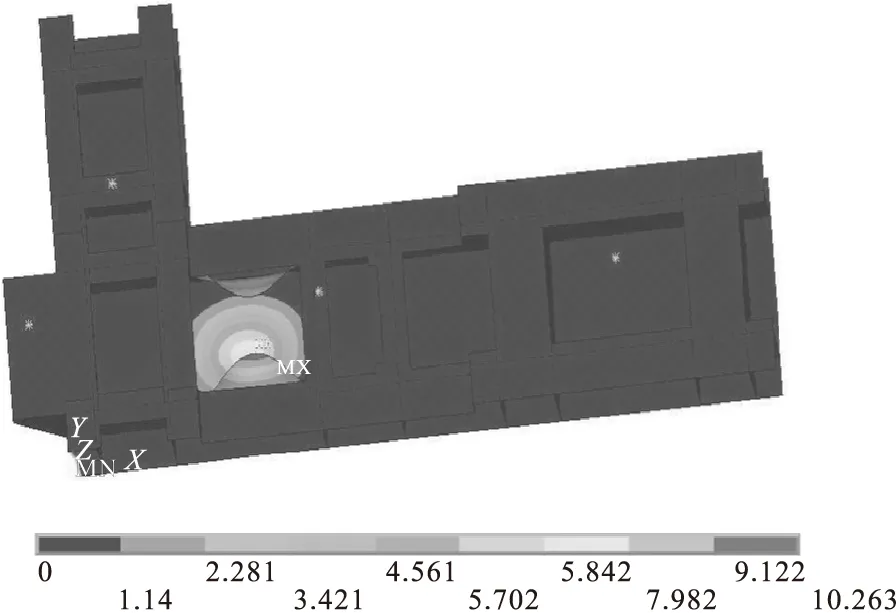
图6 第4阶振型

3 机架强迫振动分析

3.1 激振力的计算

由于电机的转子和液力耦合器的旋转件在加工或装配时会产生不可避免的误差，高速转动时就会产生在Y和Z方向的偏心，在各个瞬时位置上，这两个偏心会产生离心力，使其在运行时产生扭振，开机时产生的振动更大。

电机转子的转速n=1485r/min，旋转角速度

(1)

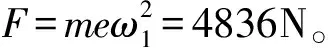
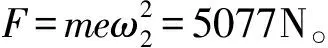
在0～2秒内电机由0r/min到1485r/min；液力耦合器在2秒时开始启动(此时电机已达到额定转速)，8秒之后液力耦合器达到1485r/min，此时电机和液力耦合器转速同步。调用Matlab/Simulink中的Simpower Systems各相关环节模块，将其连接起来，可得到三相异步电动机的仿真模型[5]，如图7所示。

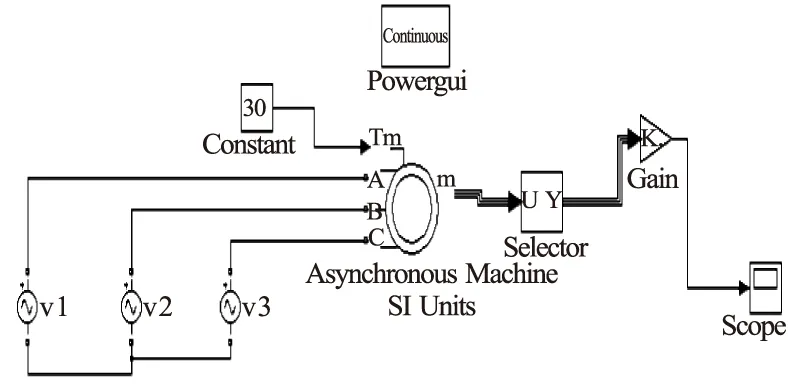
图7 电机仿真模型

图8为电机的启动曲线。从图8中可以看出，在0～2秒时电机转速和时间的曲线接近线性，所以按线性函数处理，在2秒之后曲线呈水平。电转速与时间的函数方程为

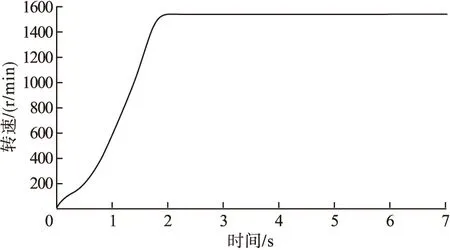
图8 电机启动曲线

液力耦合器的转速和时间的关系按照线性来施加，转速与时间的函数方程为

机架的载荷施加情况如表2所示。

3.2 结果分析

机架与电机、耦合器的螺栓连结处的节点位移随时间变化曲线分别如图9和10所示。

表2 机架的载荷

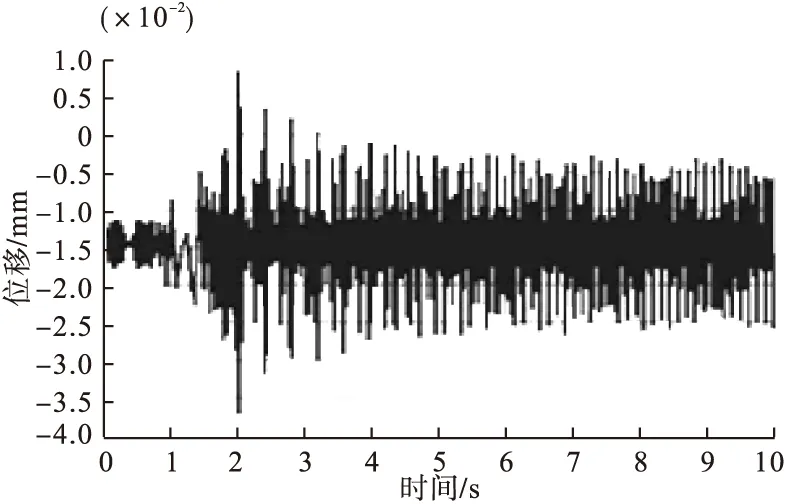
图9 电机与机架螺栓连接处的位移随时间变化曲线

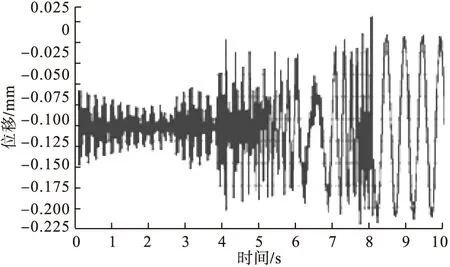
图10 耦合器与机架螺栓连接点处的位移随时间变化曲线

计算时考虑电机和耦合器的自重会改变结构的静平衡位置，但不会影响机架在静平衡位置附近作振动的规律，故图9和图10的位移曲线分别向下偏移了0.015mm和 0.11mm。

由图9可见，在电机旋转不平衡力的作用下，机架与电机的螺栓连结点在前3秒作瞬态振动，在2秒时该处有最大位移，位移为0.035mm。由于阻尼的存在，瞬态振动的持续时间很短，大约在3秒之后振动表现为稳态振动，其位移为0.026mm。根据实际工作要求，电动机架处位移不能超过0.07mm，可见此部分机架结构的位移满足实际要求。

由图10可知，耦合器2秒之前尚未启动，2秒之后才开始工作。机架与耦合器的螺栓连结点在前8秒作瞬态振动，在8秒时该点的位移有最大值，其位移值为0.22mm。根据工程设计要求，液力耦合器与机架连接处的位移不能超过实际工作要求(0.15mm)，所以耦合器在机架螺栓处位移不满足实际要求。

图11为2秒时机架结构振动位移云图，此时机架的最大位移在耦合器作用处，为0.13mm。

图11 2秒时机架结构振动位移云图

图12为8秒时机架结构振动位移云图，此时有位移最大值0.22mm，也在耦合器作用处，最大位移位置与图11所示一致，说明此处机架刚度不足，需对机架结构进行改进。

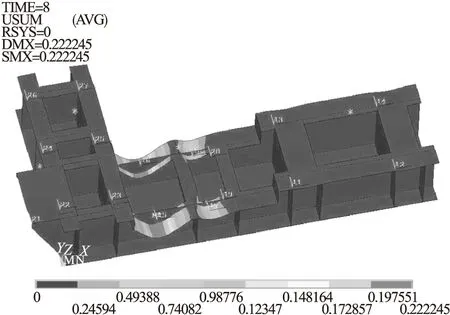
图12 8秒时机架结构振动位移云图

4 机架的结构改进

由于机架与液力耦合器连接的螺栓处在工作时位移不满足实际要求，所以对其进行改进。设计中应使受力直接导入到主承载结构上，采用直接支撑肋的方法可大幅度提高板的刚度，提高板承受弯曲的能力[6]。故在机架与液力耦合器连接刚度最小处加一肋板，肋的厚度为12mm，高度为406mm，长度为1030mm，如图13所示。

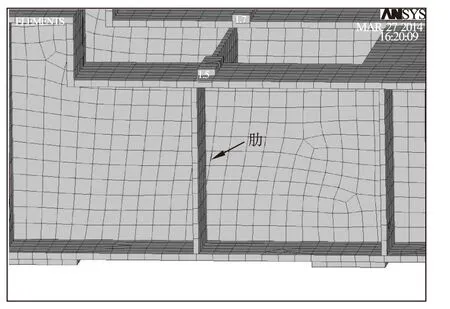
图13 肋板位置

为检查改进的效果，对改进后机架再次进行强迫振动分析计算。如图14所示，8秒时液力耦合器与机架螺栓连接点处的最大位移为0.12mm，其中耦合器自重G耦合器产生的静态位移为0.06mm。

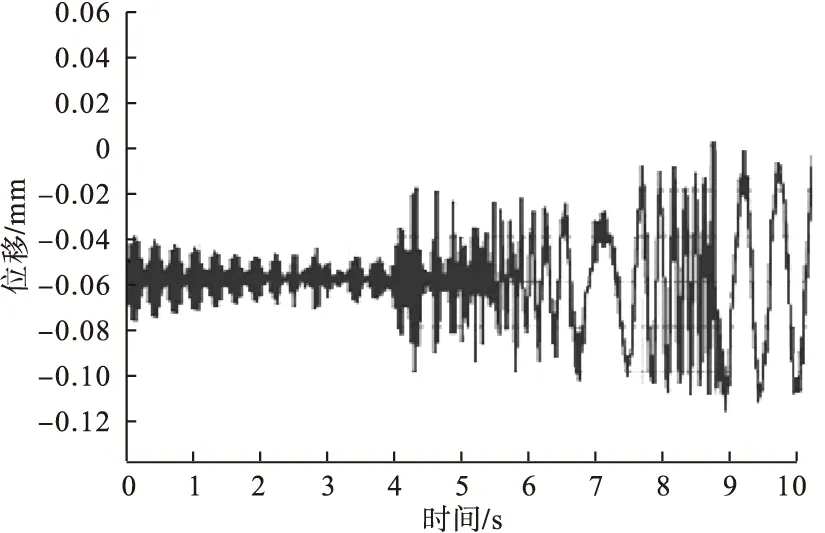
图14 液力耦合器与机架螺栓连接点处的位移随时间变化曲线

图15是改进后8秒时机架结构振动位移云图，从图中看出，耦合器与机架连接处位移明显减小，对比未加肋的耦合器与机架，最大位移减小55%，满足工程0.15mm的要求，说明改进合理。

5 结论

(1)对机架进行了固有频率分析，其第一阶固有频率为59.9Hz，而工作频率为26Hz，频率相差2.3倍，说明机架振幅过大并不是共振引起的。

图15 改进后8秒时机架结构振动位移云图

(2)分析机架在激振力作用下的瞬态振动，得到电机支座处和液力耦合器支座处的最大位移分别为0.035mm和0.22mm；根据设计规范，机架与液力耦合器连接处的位移超过了允许范围。

(3)为提高机架抗弯曲的能力，采用直接支撑肋的方法在机架与液力耦合器连接刚度最小处加一肋板，则液力耦合器支座处的最大位移减小为0.12mm，小于许用位移0.15mm，满足工程设计要求。

[1]陈远伟.大型电机上机架结构分析及优化设计[J].机电工程技术，2007，36(9)：29-31.

[2]刘建忠.利用有限元法对电机机座的分析与优化[J].防爆电机，2010，45(3)：20-23.

[3]赵凤波.香蕉形直线振动筛的疲劳分析[J].沈阳理工大学学报，2010，29(5)：56-59.

[4]王文斌,林忠钦，严隽琪,等.机械设计手册[M].北京:机械工业出版社，2008.

[5]黄文新.笼型异步发电机的MATLAB仿真模型[J].中小型电机，2002，29(1)：1-3.

[6]B.克莱恩.轻量化设计-计算基础与构件优化[M].北京:机械工业出版社，2010：11-12，29-31.

(责任编辑：赵丽琴)

Dynamic Modification of a Vibrating Screen Based on Dynamic Sensitivity Analysis

AN Xiaowei,LIU Qin

(Shenyang Ligong University,Shenyang 110159,China)

A parameterized modeling method is adopted to establish the finite element model of belt conveyor drive frame.First of all,natural features of the rack is calculated.Forced vibration analysis was carried out on the rack,to calculate the amplitude of the rack on the job.By analyzing the amplitude curves,determine the position of frame vibration.On this basis,the design of frame structure is improved.

frame;finite element;dynamics simulation;improved structure

2014-09-19

安晓卫(1956—)男，教授，研究方向：机械振动和优化.

1003-1251(2015)06-0042-05

TH113.1

A