万有引力搜索算法改进及仿真验证

杨 青，张金格，吉孟然

(沈阳理工大学 自动化与电气工程学院，辽宁 沈阳 110159)

万有引力搜索算法改进及仿真验证

杨 青，张金格，吉孟然

(沈阳理工大学 自动化与电气工程学院，辽宁 沈阳 110159)

针对万有引力搜索算法(GSA)求解函数优化问题时易陷入局部最优且优化精度不高的问题，提出一种改进的万有引力搜索算法(IGSA)。IGSA算法引入了时变权重和边界变异策略，改善了全局搜索能力和局部优化能力。通过求解无约束优化问题进行仿真验证，结果表明，改进的万有引力搜索算法具有更好的优化性能。

优化算法；搜索算法；GSA；IGSA

针对特定的复杂计算，学者们提出很多启发式优化算法，但目前均未有一种算法能成功解决所有优化问题，因此探索新的启发式智能搜索算法十分必要。

万有引力搜索算法(Gravitational Search Algorithm，GSA)由Esmat Rashedi教授等人在2009年提出[1]，是源于对物理学中的万有引力进行模拟产生的启发式智能群体优化算法。目前关于万有引力算法的研究已经成为热点，理论研究方面，文献[2-5]从不同角度对GSA算法进行改进以增强其优化性能；在应用方面，文献[6]将改进的GSA用于微网优化问题的求解，文献[7]采用GSA对电力系统控制变量进行优化调整，文献[8]中提出自适应量子的二进制引力搜索算法优化电能质量检测仪位置，文献[9]将GSA与径向基神经网络相结合用于解决配电变电所输电问题。GSA在解决问题的同时也存在局部优化能力差和早熟收敛的问题[6，10]。因此，本文提出了改进的万有引力搜索算法(ImprovedGravitationalSearchAlgorithm，IGSA)。为验证IGSA的优化效果，文中针对常用的优化问题，通过仿真实验，将IGSA与GSA、PSO算法的优化算法结果进行比较。

1 标准万有引力搜索算法

GSA来源于物理学中的万有引力定律“宇宙中任意2个质点通过连心线方向上的力相互吸引，该引力的大小与它们质量的乘积成正比，与它们距离的平方成反比，与两物体的化学组成和其间介质种类无关”。万有引力会使物体朝着质量最大的物体移动如图1所示，而最大质量的物体占据最优位置，从而求得优化问题的最优解[1]。在GSA中，每个个体均包含5个特征参数：位置、速度、惯性质量、主动引力质量及被动引力质量，物体的位置即为问题的解。

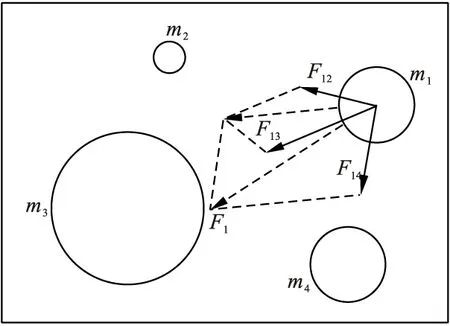
图1 各物体对m1的作用

假设在D维搜索空间中有N个个体，定义第i个个体的位置和速度分别为

(1)

i=1,2,…,N;k=1,2,…,D

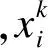
(2)

式中：Mpi(t)指被作用个体i的惯性质量；Maj(t)指作用个体j的惯性质量；ε代表较小正常量；G(t)指t时刻的万有引力常量，其值随宇宙实际年龄的增大而变小，表达式为

G(t)=G0×e-αt/T

(3)

式中：G0指t0时刻的万有引力常量，通常取值为100；α为衰减系数，通常取为20；T表示最大迭代次数。Rij(t)表示个体i和个体j间的欧氏距离：

Rij(t)=‖Xi(t),Xj(t)‖2

(4)

从而得到t时刻，个体i在k维空间上受到的总的作用力为

(5)

式中rand是[0，1]内的一个随机数。根据牛顿第二定律，t时刻个体i在第k维上的加速度为

(6)

式中Mii(t)表示在t时刻个体i的惯性质量。

GSA在每次迭代过程中，个体的速度和位置根据以下公式进行更新，即

(7)

个体的惯性质量根据其适应值的大小来计算，惯性质量越大表明它越接近最优值，同时也意味着该个体的吸引力越大，但其移动速度却越慢。假设引力质量与惯性质量相等，个体的质量可以通过适当的运算规则去更新，更新算法如下所示：

(8)

式中，fiti(t)表示个体i在t时刻的适应值，best(t)和worst(t)根据具体情况而定。当求最小值问题时，定义如下：

(9)

当求最大值问题时，定义如下：

(10)

2 改进的万有引力搜索算法

本文提出改进GSA(Improved Gravitational Search Algorithm，IGSA)优化算法，分别从时变权重和边界变异两方面对GSA优化算法进行改进，详细分析如下。

2.1 基于时变权重的GSA优化算法

GSA优化算法探索能力和开发能力的平衡是靠惯性权重来实现的。较大的惯性权重使个体在原来的方向上具有更大的速度，具有更好的探索能力；较小的惯性权重使个体继承了较少的原方向的速度，具有更好的开发能力。通常希望种群在开始时具有较好的探索能力，随着迭代次数的增加，特别是临近结束时希望具有较好的开发能力。针对此情况本文提出动态调节惯性权重的GSA优化算法。设置惯性权重的取值范围为[wmin,wmax]，最大迭代次数为T，则在t时刻惯性权重为

(11)

这是一种线性减小的变化方式。根据实际问题来确定最大权重wmax和最小权重wmin。则公式(7)转化为

(12)

2.2 基于边界变异的GSA优化算法

在GSA工作过程中，个体在牛顿第二定律作用下若其位置超出可行域[xmin,xmax]的范围，标准GSA会强制将个体位置拉回其边界上，即xi=xmax或xi=xmin。实际应用中，若个体位置过多地聚集到可行域边界上，不利于GSA的收敛。为提高算法收敛性，本文引入边界变异策略，详细描述为

若xi≥xmax或xi≤xmin

xi=rand×(xmax-xmin)+xmin

(13)

经边界变异后，超过边界的个体将不会全部聚集到边界上，而是重新分布在[xmin,xmax]可行域范围内，增加了个体的多样性，利于算法更快地发现最优解。

2.3 IGSA流程图

IGSA工作过程如下：

(1)初始化：确定搜索空间维数D，种群规模N，迭代次数T，初始时刻万有引力常数G0，衰减系数α，随机初始化种群位置和速度；

(2)计算每个个体的适应值fiti(t)；

(3)分别根据式(3、8、10)更新G(t)、Mi(t)、best(t)和worst(t)；

(6)根据式(13)进行边界变异；

(7)判断是否达到终止条件，若是则停止，否则转至(2)，一般终止条件设置为一个足够好的适应值或达到预设的最大迭代次数。

IGSA流程图如下：

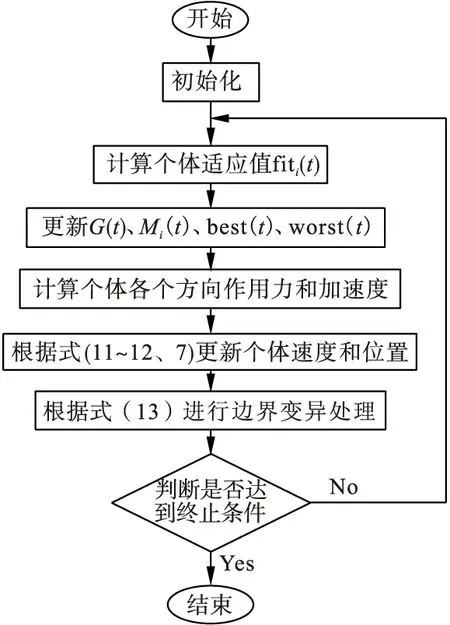
图2 IGSA流程图

3 仿真实验与结果分析

3.1 典型优化问题

本文通过求解无约束优化问题

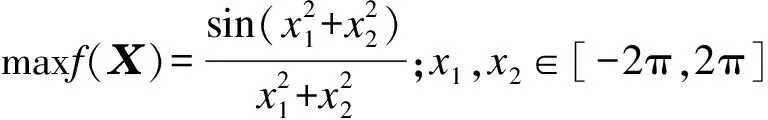
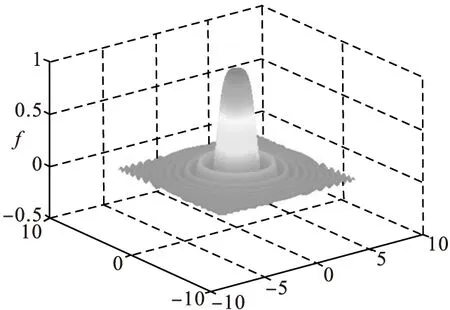
图3 目标函数的三维曲面图

选用上述目标函数作为测试函数，其特点是该函数是多峰函数，即在[-2π,2π]上具有多个极大点和极小点，但只有一个全局极大值，且在全局极大值临近的狭小区域内取值变化缓慢，部分优化算法在优化该函数时，易陷入局部最优，即该函数可以评价优化算法的搜索性能。

3.2 IGSA参数设计

编码：显然问题的维数为2，即每个个体为2维的实数向量；

初始化范围：根据问题要求，设定为[-2π,2π]，初始速度设为0；

初始化参数：G0=100，α=20，λ=1；

种群大小：为了方便说明，采用一个较小的种群规模，N=5；

停止准则：设定为最大迭代次数100次，显然该问题的最优值为1，因此设定阈值为1。

3.3 仿真验证及分析

图4给出采用IGSA算法种群全局最优适应度值随着迭代次数增加的变化曲线。结果表明，经过51次迭代后，种群收敛，最优位置为(0，0)，最大值为1，这与理论分析相同，验证了IGSA算法的可行性。

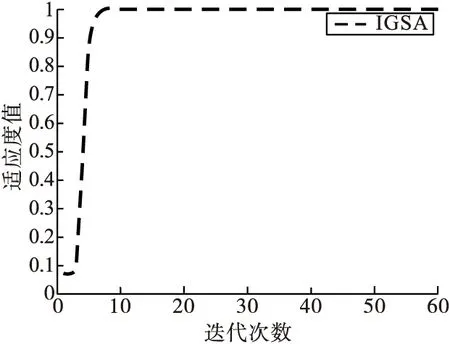
图4 IGSA全局最优适应度值曲线

IGSA与GSA、PSO算法进行比较分析如下：

1)全局最优适应度值比较如图5所示。

定性分析：IGSA优化算法在51次迭代时停止循环，而GSA、PSO算法在达到预定的最大迭代次数100时停止，表明IGSA较GSA、PSO算法有较快的收敛速度；

定量分析：IGSA优化算法最终达到最优值1，而PSO算法在运行100次之后全局最优值为0.9999，尽管相差0.0001，但也表明了IGSA较PSO算法更精确，GSA算法显然没有找到最优解。

2)个体历史最优适应度值比较曲线如图6～10所示。

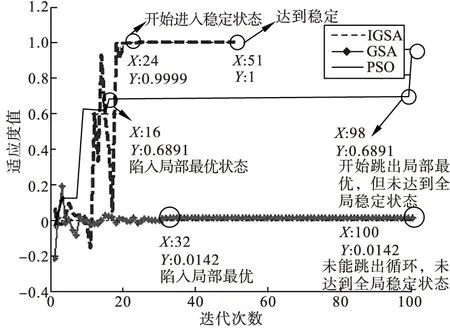
图6 第1个个体历史最优值曲线

从图6～10中可以看出，IGSA优化算法在可行域范围内进行全局搜索，最终使得每个个体均取得最优值，即种群收敛，而PSO算法在循环过程中，总在个体历史最优值附近徘徊，这样就降低了种群的全局搜索能力，以个体1为例，在进行100次迭代时还未达到最优值，即种群还未收敛；GSA算法尽管在100次迭代后收敛，但是未达到最优值。另外IGSA优化过程中每个个体适应度值的波动体现出IGSA算法的全局搜索能力，避免了陷入局部最优问题。

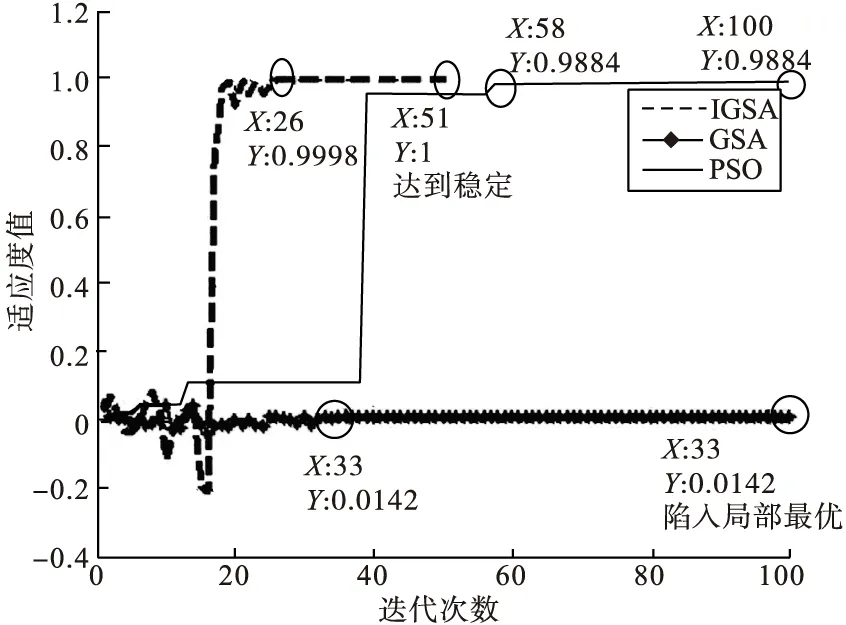
图7 第2个个体历史最优值曲线

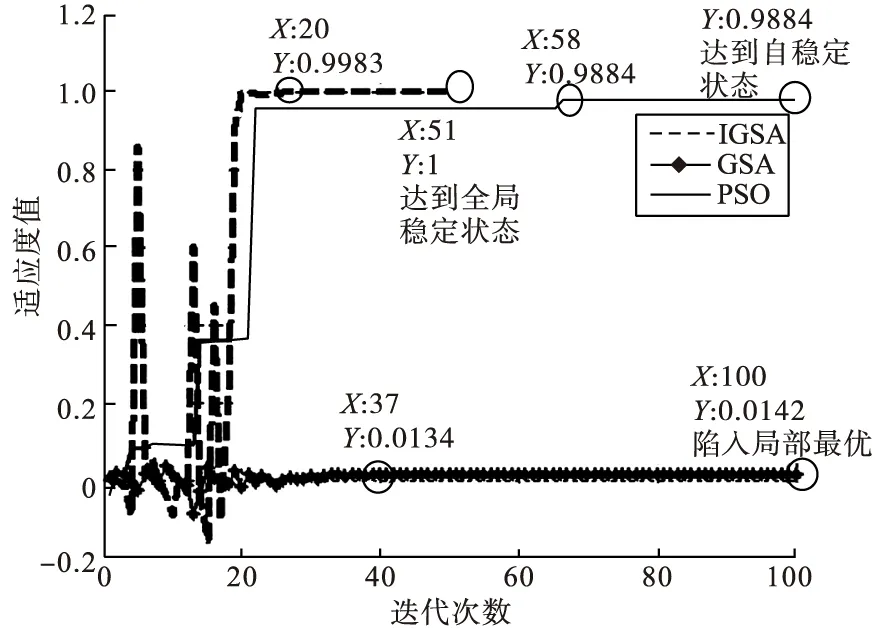
图8 第3个个体历史最优值曲线

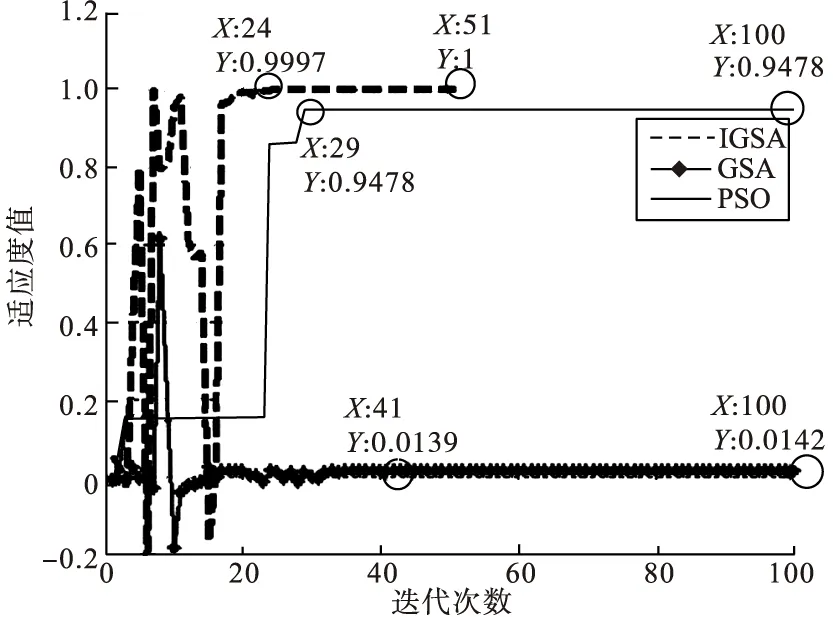
图9 第4个个体历史最优值曲线

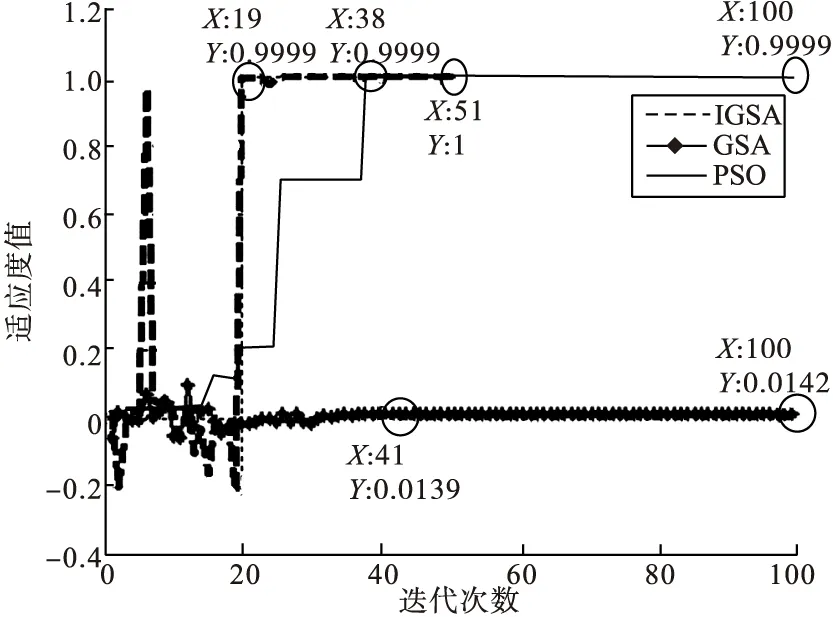
图10 第5个个体历史最优值曲线

4 结束语

提出了改进万有引力搜索算法，即IGSA。通过引入时变权重及边界变异策略对GSA算法进行了改进。通过仿真实例对IGSA算法进行测试。与GSA、PSO算法相比，IGSA均表现出更好的优化精度与稳定性，这表明IGSA具有良好的全局搜索能力且不易陷入局部最优值。

[1]Esmat Rashedi，Hossein Nezamabadi-pour，Saeid Saryazdi.GSA：A Gravitation Search Algorithm[J].Informaton Science，2009，(179)：2232-2248.

[2]杨晶，黎放，狄鹏.免疫万有引力搜索算法的研究与仿真[J].兵工学报，2012，33(12)：1533-1538.

[3]Anupam Yadav，Kusum Deep.Constrained Optimization Using Gravitational Search Algorithm[J].National Academy Science Letters，2013，36(5)：527-534.

[4]Yong Liu，Liang Ma.Improved gravitation search algorithm based on free search differential evolution[J].Journal of systems Engineering and Electronics，2013，24(4)：690-698.

[5]Mohammad Bagher Dowlatshahi，Hossein Nezamabadi-pour，Mashaallah Mashinchi.A discrete gravitational search algorithm for solving combinatorial optimization problems[J].Information Sciences，2014，(258)：94-107.

[6]李鹏，徐伟娜，周泽远,等.基于改进万有引力搜索算法的微网优化运行[J].中国电机工程学报，2014，34(19)：3073-3079.

[7]Arup Ratan Bhowmik，A.K.Chakraborty.Solution of optimal power flowusing nondominated sorting multiobjective Gravitation Search Algorithm[J].International Journal of Electrical Power & Energy System，2014，(62)：323-334.

[8]Ahmad Asrul Lbrahim，Azah Mohamed，Hussain Shareef.Optimal power quality monitor placement in power system using an adaptive quantum-inspired binary gravitional search algorithm[J].International Journal of Electrical Power & Energy System，2014，(57)：404-413.

[9]Y.Mohamed Shuaib，M.Surya Kalavathi，C.Christober Asir Rajan.Optimal capacitor placement in radial distribution system using Gravitation Search Algorithm[J].International Journal of Electrical Power & Energy System，2015，(64)：384-397.

[10]Tapabrata Chakraborti，Kaushik Das Sharma，Amitava Chatterjee.A novel local extrema based gravitational search algorithm and its applicati on in face recognition using one image per class[J].Engineering Applications of Artificial Intelligence，2014，(34)：13-22.

(责任编辑：马金发)

Improvement and Simulation of Gravitation Search Algorithm

YANG Qing，ZHANG Jinge，JI Mengran

(Shenyang Ligong University，Shenyang 110159，China)

To solve the problem of falling into local optimal value and the low accuracy in the function optimization by using the Gravitation Search Algorithm (GSA),an improved Gravitation Search Algorithm (IGSA) is proposed.Variable weight and boundary mutation strategy are introduced in the proposed method,which improves the global search ability and local optimization capability.Simulation result of solving the unconstrained optimization problem demonstrates that the proposed algorithm has much better optimization performances.

optimization algorithm;search algorithm;GSA;IGSA

2014-09-30

辽宁省教育厅科学研究项目(L2014083)；辽宁省教育厅科学研究项目(L2015467)

杨青(1963—)，男，教授，研究方向：故障检测与诊断等.

1003-1251(2015)06-0066-06

文献标志码：A