基于功率谱熵的频谱感知算法研究*

高　燕，胡国兵，张照锋，金　明，汤　滟

(1.南京信息职业技术学院电子信息学院，南京210023; 2.英国华威大学工程学院，考文垂CV4 7AL;3.河海大学计算机与信息学院，南京210098)



基于功率谱熵的频谱感知算法研究*

高燕1，2，胡国兵1，3*，张照锋1，金明1，汤滟1

(1.南京信息职业技术学院电子信息学院，南京210023; 2.英国华威大学工程学院，考文垂CV4 7AL;
3.河海大学计算机与信息学院，南京210098)

摘要:针对低信噪比条件下认知无线电频谱感知问题，提出了一种基于功率谱熵的频谱检测算法。在分析主用户信号空闲与占用两种不同条件下观测信号功率谱熵差异的基础上，将其作为检验统计量，并确定了相应的判决门限，以实现对主用户信号频谱是否空闲的判决。计算机仿真结果表明，本算法无需信号的先验信息，可在较低信噪比条件下实现对常用调制信号的频谱感知，与盒维数频谱感知方法相比，检测性能约有8 dB的改进。

关键词:认知无线电;频谱感知;功率谱熵;噪声不确定度;离散傅里叶变换

项目来源:江苏省自然科学基金课题项目(BK2011837);江苏省“333高层次人才培养工程”项目(BRA2013171)，江苏省高校优秀中青年骨干教师和校长境外研修计划项目;南京信息职业技术学院科研基金课题项目(YKJ12－007);江苏省青蓝工程项目

近年来，随着无线通信技术的飞速发展，无线通信业务量的不断增大与无线频谱资源紧张的矛盾日益凸显。认知无线电CR(Cognitive Radio)技术［1］是解决这一问题的重要方法，其核心技术就是频谱感知。频谱感知通常需要认知用户在无主用户信号的先验信息及低信噪比条件下，对主用户信号频谱占用状态进行有效可靠的检测，已成为认知无线电信号处理领域的热点课题。

传统的频谱感知方法主要包括能量感知法［2－3］、匹配滤波器检测［4］、循环平稳特征检测［5］等。能量感知法无需信号的先验信息，简单易于实现，但易受噪声不确定度的影响，在低信噪比条件下检测性能变差。匹配滤波器检测是一种性能最优的检测器，但其实现复杂，且需要主用户信号的先验信息。循环平稳特征检测性能优于能量感知法，但计算量较大，检测时间较长，从而降低了系统的灵敏度。近年来，众多学者将非线性特征分析引入到认知无线电频谱感知中，一定程度上改善了频谱感知算法的性能。文献［6］提出了一种基于匹配滤波器的输出序列时域熵的频谱感知方法，其主要依据为:当主用户信号频谱空闲时，观测信号的时域熵值较大，而主用户信号频谱被占用时，其熵值较小。然而，该方法仅适用于主用户的先验信息已知情况下。文献［7－8］提出了一种基于频域熵的频谱感知算法，通过将频域熵与门限值比较以检验主用户信号存在与否，与传统的能量感知法、循环平稳特征检测方法相比，该方法的检测性能有了进一步的提高。但检验统计量频域熵在实际计算时，需要事先确定对信号频谱的分段数，而最佳分段数通常需要进行大量仿真确定，且受信号调制方式及参数变化的影响较大，从而影响算法的韧性。文献［9］提出了一种基于特征值检测的频谱感知算法，该方法需要从接收信号的协方差矩阵中提取特征值作为检验统计量，计算复杂度较高。文献［10］在分析噪声与信号盒维数之间差异的基础上，提出了一种基于分形盒维数特征的频谱感知算法。但该方法在低信噪比条件下，性能下降明显。

功率谱熵作为表征信号复杂度的非线性特征量，已广泛用于语音端点检测［11］，医学脑电信号的处理［12－13］，机械故障诊断［14］等信号处理领域。本文将其应用于认知无线电信号的频谱感知中，提出了一种新的基于非线性特征分析的频谱检测算法。先对接收到的观测信号利用离散傅里叶变换得到其功率谱，然后进行归一化处理，并计算出功率谱熵作为检验统计量。计算机仿真结果表明，本算法可在无信号先验信息及低信噪比条件下，实现对常用调制信号的频谱检测，且检测性能优于基于盒维数的频谱感知方法。

1　算法描述

1.1信号模型

假设主用户信号的频谱感知问题可建模为如下二元假设检验问题:

式中:x(n)表示接收到的观测信号，s(n)表示主用户的发送信号，w(n)表示方差为σ2的复加性高斯白噪声AWGN(Additive White Gaussian Noise)，N为信号样本长度。H0表示频段空闲，可以被认知用户使用; H1表示频段被占用，认知用户不可接入该频段。

1.2基于功率谱熵的频谱感知算法

假设观测信号x(n)中每个样本出现的概率为

则该信号的信息熵可表示为

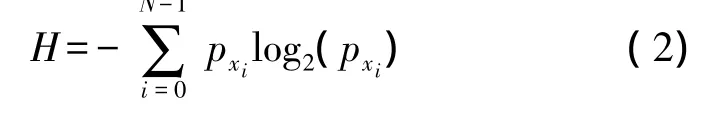
应用信息熵的概念来定量计算信号功率谱的不确定性称为“功率谱熵”［15］，其具体的计算步骤如下:

(1)利用离散傅里叶变换得出信号的功率谱:

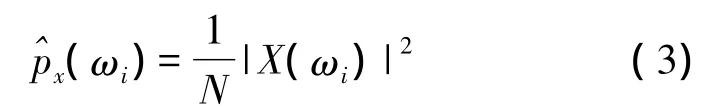
式中:X(ωi)为信号x(n)中每个样本的离散傅里叶变换。

(2)将功率谱^px(ωi)按总的谱功率进行归一化可得:

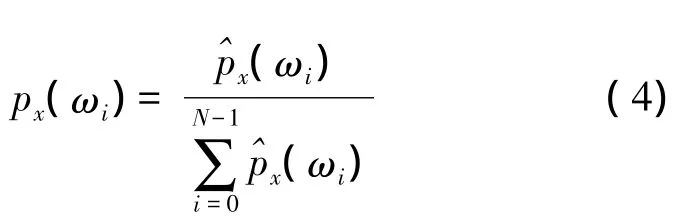
(3)计算出相应的功率谱信息熵，简称功率谱熵:

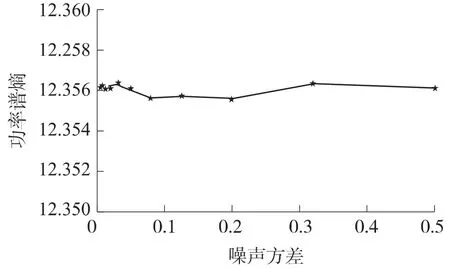
图1　不同方差时高斯白噪声的功率谱熵

功率谱熵可作为时间不确定性的一种度量，同时也反映了信号的不确定性。一般而言，若观测信号中不含主用户信号，仅有噪声时，其功率谱熵值就较大;反之，若包含主用户信号，功率谱熵值则较小。该结论可通过仿真实验进行验证。考虑在加性高斯白噪声(AWGN)信道下，选择BPSK、2FSK、QPSK、MSK、2ASK 5种调制信号作为待测信号，码速率Rs= 600 byte/s，采样频率fs=48 kHz，2FSK信号的两个码元信号对应的载波频率分别为fc1= 2 kHz和fc2= 6 kHz，BPSK、QPSK、MSK和2ASK 4种信号的载波频率为fc=4 kHz，信号样本长度N = 8 000。图1所示为H0假设下，当高斯白噪声的方差在0.005～0.500之间变化时的功率谱熵，由图1可知，高斯白噪声的功率谱熵基本维持在12.35左右。图2所示为H0和H1两种不同假设下的功率谱熵。由图2可见:(1)对于前述的5种不同的调制信号，在H1假设下，功率谱熵会随着信噪比SNR(Signal-to-Noise Ratio)的变化而变化，在适度信噪比范围内，两种不同假设下的功率谱熵存在着差异，且随着信噪比的增加，两者差异明显。如信噪比大于－15 dB时，观测信号的功率谱熵小于噪声的功率谱熵，所得结论与前述的分析相符; (2)对于5种不同的调制信号，其功率谱熵也有所区别，相同的信噪比条件下，BPSK和2ASK信号的功率谱熵较大，2FSK、QPSK和MSK 3种信号的功率谱熵相差较小。

图2　不同信噪比条件下信号和噪声的功率谱熵

基于功率谱熵的频谱感知算法的首要任务是计算出接收信号的功率谱熵得到检验统计量T［x(n)］，而后设定虚警概率PFA以确定判决门限λ，将两者作比较，以判断主用户信号是否存在。两种不同假设下的检验统计量可以表示为

式中:λ为判决门限。这里，将H0假设下的功率谱熵表示为T［x(n) |H0］，假设所估计的噪声的功率谱熵服从均值为T［x(n) |H0］，方差为σ2e的高斯分布，则判决门限可由式(7)确定:

2　性能仿真与分析

下面通过仿真方法分析本文提出的功率谱熵频谱感知算法的统计性能。每种条件下的仿真次数为1 000次。仿真中考虑在加性高斯白噪声(AWGN)信道下，信号码速率Rs=600 byte/s，采样频率fs=48 kHz。

由于无线环境的实时变化，信道中的噪声存在着不确定性，因此需要研究不确定性噪声对检测器性能的影响。假设所估计的噪声不确定度模型为，其中表示噪声功率的估计值，σ2为真实的噪声功率，α为噪声不确定度(α＞1)，以dB形式表示为β=10lgα。图3所示为噪声不确定度分别为β=0 dB，1 dB，0.5 dB时本文算法和文献［10］提出的盒维数法感知性能的对比图。仿真条件:主用户信号为BPSK信号，载波频率为fc=4 kHz，信号样本长度N=8 000，虚警概率PFA=0.1，信噪比从－20 dB变化到20 dB，步长2 dB。由图3可见:(1)当信号样本长度及虚警概率一定时，两种方法的检测概率PD都随着信噪比的增加而变大，且无论噪声是否存在不确定度，本文算法的检测性能都明显优于盒维数检测方法。例如，噪声不确定度β=0 dB时，当信噪比SNR大于－7 dB时，文献［10］方法的检测概率PD大于0.9，而同等条件下，本文算法在信噪比SNR大于－15 dB，可达到同等的检测性能，约有8 dB的改进，说明本文算法实现有效频谱感知的信噪比门限低于文献［10］方法; (2)当存在一定噪声不确定度时，本文算法具有一定的韧性，且从噪声不确定度对检测性能的影响程度来看，本文算法仍优于文献［10］方法。例如，在噪声不确定度β=1 dB条件下，信噪比大于－13 dB时，本文算法的频谱检测概率PD可达0.9以上，且基本不受噪声方差波动的影响;而同样噪声不确定度时，当信噪比大于－5 dB时，文献［10］方法才能达到同样的性能。

图3　不同噪声不确定度时两种方法的检验性能比较

图4所示为本文算法的接收机工作特性曲线ROC(Receiver Operation Characteristic Curves)与信号样本长度的关系及其与文献［10］方法的性能比较。仿真条件:信噪比SNR=－16 dB，样本长度分别取N=9 600，8 000，6 400，4 800，噪声不确定度β=0 dB，其他参数与图3相同。由图4可见，相同信噪比条件下，信号样本长度越大，本文算法的检测概率越高。此外，N= 4 800时本文算法性能优于N= 8 000时文献［10］提出的盒维数检测器的性能，说明在同等的检测性能条件下，本文算法所需的信号样本长度要少于文献［10］的方法。

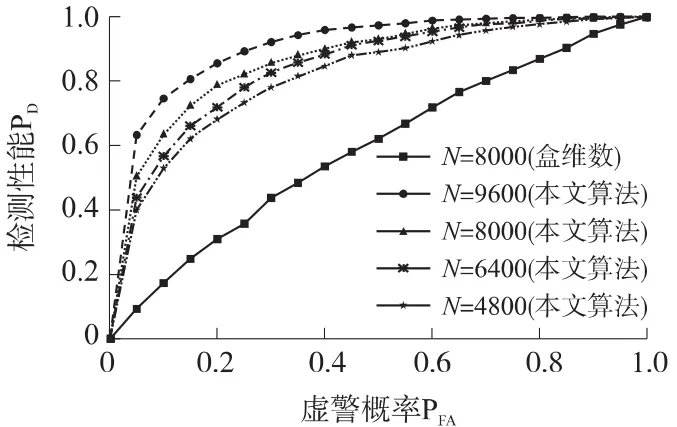
图4　不同信号样本长度时的ROC性能比较

图5所示为本文算法的检测性能受调制信号样式变化影响的示意图。仿真条件中调制信号分别为BPSK、2FSK、QPSK、MSK、2ASK 5种样式，噪声不确定度β=0 dB，其他参数与图3相同。由图5可见，信噪比较低时(SNR小于－12 dB)，对于不同的调制信号，本文算法的检测性能略有差异，如2FSK信号的检测性能最好，QPSK和MSK信号的检测性能次之，而2ASK和BPSK信号的检测性能略低，由节1的仿真分析可知，造成这种差异的原因在于不同调制信号样式的信号复杂度不同，其功率谱熵也不同。但当信噪比大于－14 dB以上，5种调制信号的检测概率基本都能达到96%以上。

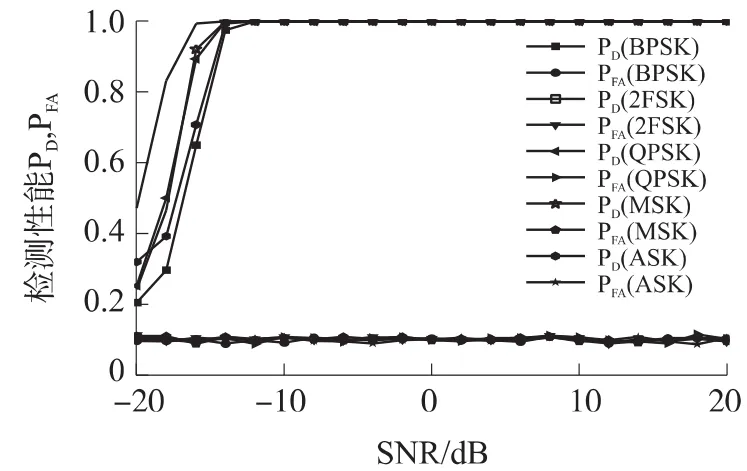
图5　不同调制信号的检测性能比较

3　结论

本文提出了一种基于功率谱熵的频谱感知算法，以观测信号的功率谱熵作为检验统计量，可实现对主用户信号的频谱感知。仿真结果表明，本文算法可在无信号先验信息、低信噪比及适度的噪声不确定度条件下，对主用户信号的频谱占用状态进行有效检测，其性能优于盒维数频谱感知方法。

参考文献:

［1］Haykin S.Cognitive Radio:Brain-Empowered Wireless Communications［J］.IEEE Journal on Selected Areas in Communications，2005，23(2) :201－220.

［2］Urkowitz H.Energy Detection of Unknown Deterministic Signals ［J］.Proceedings of the IEEE，1967，55(4) :523－531.

［3］López-Benítez M，Casadevall F.Improved Energy Detection Spectrum Sensing for Cognitive Radio［J］.Communications，IET，2012，6(8) :785－796.

［4］Cabric D，Mishra S M，Brodersen R W.Implementation Issues in Spectrum Sensing for Cognitive Radios［C］/ /Proc of 38th Asilomar Conf Signals，System，and Computers，Monterey，CA，Nov.2004:772－776.

［5］Zhuan Y，Grosspietsch J，Memik G.Spectrum Sensing Using Cyclostationary Spectrum Density for Cognitive Radios［J］.Proc IEEE Workshop Signal Processing Systems，October 2007:1－6.

［6］Nagaraj S V.Entropy Based Spectrum Sensing in Cognitive Radio ［J］.Signal Process，2009，89(2) :174－180.

［7］Zhang Y，Zhang Q，Wu S.Entropy-Based Robust Spectrum Sensing in Cognitive Radio［J］.Communications，IEEE Transactions on，2010，4(4) :428－436.

［8］Zhang Y L，Zhang Q Y，Melodia T.A Frequency-Domain Entropy-Based Detector for Robust Spectrum Sensing in Cognitive Radio Networks［J］.IEEE Communication Letters，2010，14(6) :533－535.

［9］雷可君，杨喜，彭盛.认知无线电中基于特征值检测的频谱感知算法［J］.传感技术学报，2012，25(6) :771－777.

［10］赵春晖，马爽，杨伟超.基于分形盒维数的频谱感知技术研究［J］.电子与信息学报，2011，33(2) :475－478.

［11］王辉，袁淑丹.基于EMD与功率谱熵的语音端点检测［J］.电声技术，2013，45(33) :122－131.

［12］任亚莉.基于功率谱熵和频带能量的运动意识任务分类研究［J］.计算机应用与软件，2010，27(12) :105－111.

［13］Yang B，Zhang A H.Power Spectral Entropy Analysis of EEG Signal Based-on BCI［C］/ /Control Conference(CCC)，2013 32nd Chinese，2013，7:4513－4516.

［14］费成巍，柏树生，白广忱，等.转子振动故障的过程功率谱熵特征分析与定量诊断［J］.航空发动机，2011，37(1) :48－51.

［15］Shri P T K，Sriraam N.EEG Based Detection of Alcoholics Using Spectral Entropy with Neural Network Classifiers［C］/ /Biomedical Engineering(ICoBE)，2012 International Conference on，2012，2:89－93.

［16］López-Ben1tez M，Casadevall F.Signal Uncertainty in Spectrum Sensing for Cognitive Radio［J］.Communications，IEEE Transactions on，2013，61(4) :1231－1241.

高　燕(1981－)，女，汉族，江苏扬州人，南京信息职业技术学院讲师，硕士，主要研究方向为无线通信，认知无线电，gaoyan@njcit.cn，gyzwpp@gmail.com;

胡国兵(1978－)，副教授，博士，主要研究方向为智能信号处理;

张照锋(1974－)，副教授，硕士，主要研究方向为微波技术，通信与信号处理。

The Design and Implementation of FPGA Based on Adaptive Pixel Improved Segmentation Algorithm

DING Qianwen*
(Wuxi Professional College of Science and Technology，Wuxi Jiangsu 214028，China)

Abstract:In order to solve the accuracy problem of moving object prospect detection，an improved adaptive pixel segmentation system based on FPGA was proposed.The proposed system can optimize the test results by constructing new background model and foreground segmentation detection technology.The traditional adaptive pixel segmentation algorithm was adjusted and revised，in order to complete the hardware implementation on FPGA platform.The hardware test has be completed in Xilinx virtex 7 FPGA platform.The test results show that the function index of the proposed design are better than other algorithms，the detection accuracy is 71.4%，and average power consumption is 6.452 W which can achieve real-time processing resolution of 720×576 video stream in 50 frame/s.

Key words:target detection; FPGA; adaptive; background modeling

中图分类号:TP302

文献标识码:A

文章编号:1005－9490(2015) 03－0506－04

收稿日期:2014－06－29修改日期:2014－07－24

doi:EEACC:6140C10.3969/j.issn.1005－9490.2015.03.008