砂轮测量用白光干涉仪三维运动机台设计

2015-02-24钟浩明崔长彩

杭州师范大学学报(自然科学版) 2015年1期

关键词：有限元分析

钟浩明，崔长彩，余　卿

(华侨大学机电及自动化学院，福建厦门 361021)

砂轮测量用白光干涉仪三维运动机台设计

钟浩明，崔长彩，余卿

(华侨大学机电及自动化学院，福建厦门 361021)

摘要：为了实现对工件表面质量进行预测和控制，对砂轮表面的三维形貌测量、表征和评价就显得尤为重要.设计了一款砂轮检测用白光垂直扫描干涉仪三维运动机台，主要分为XY向位移平台部分、砂轮旋转定位部分、桥式立柱部分以及含有柔性铰链的Z向微位移系统部分,通过有限元静动力学分析优化机台结构，使其满足使用要求.实现XY向位移平台单脉冲步长0.3125 μm，Z向精级机构行程15 μm，精度0.03 μm.

关键词：白光干涉仪; 有限元分析; 位移平台

随着微纳米技术的发展，现代机械制造、检测、信息技术、材料科学等领域发生了革命性的变化，迅速向微小化、集成化、超精密方向发展，因此，在前沿科学和工程领域对精密位移技术的需求与日俱增.大行程、高分辨率、位移计量是精密位移平台的三个关键性能指标[1].清华大学精密仪器及机械学系研制的亚微米弹性微位移工作台、分别控制两个压电驱动器的变形、获得X方向和Y方向的微位移,定位精度达到±0.03 μm[2].天津大学精密仪器与光电子工程学院也研制了类似的系统，定位精度达到了0.01 μm[3].

磨削加工，在机械加工隶属于精加工，加工量少、精度高.对工件的影响体现在切削力、磨削深度、功率消耗、磨削温度以及磨削工件表面质量等[4].白光垂直扫描干涉法作为一种常用的表面形貌光学测量法，具有高精度、大量程、相位不模糊、非接触、面扫描的特点，在对表面进行三维形貌测量时所需的时间短、稳定性高.通过白光干涉原理对砂轮表面的形貌测量来实现对切削质量的控制，从而达到提高工件质量的要求.因此，本文致力于研制一款砂轮表面形貌检测用、满足精度要求的白光垂直扫描干涉仪三维运动机台.XY位移平台采用层叠式设计，Z向部分含粗精级运动并且共用一套光栅计量组件.在整体机台的设计过程中，应综合考虑白光干涉仪光学检测部分对行程、精度、分辨率的要求以及砂轮尺寸大小来决定采用何种结构，同时尽可能简化机械结构，减小外形尺寸，使其易于加工.

1机台整体结构设计

白光干涉仪三维运动机台结构分为两部分，包括砂轮承载台及立柱部分，如图1所示.

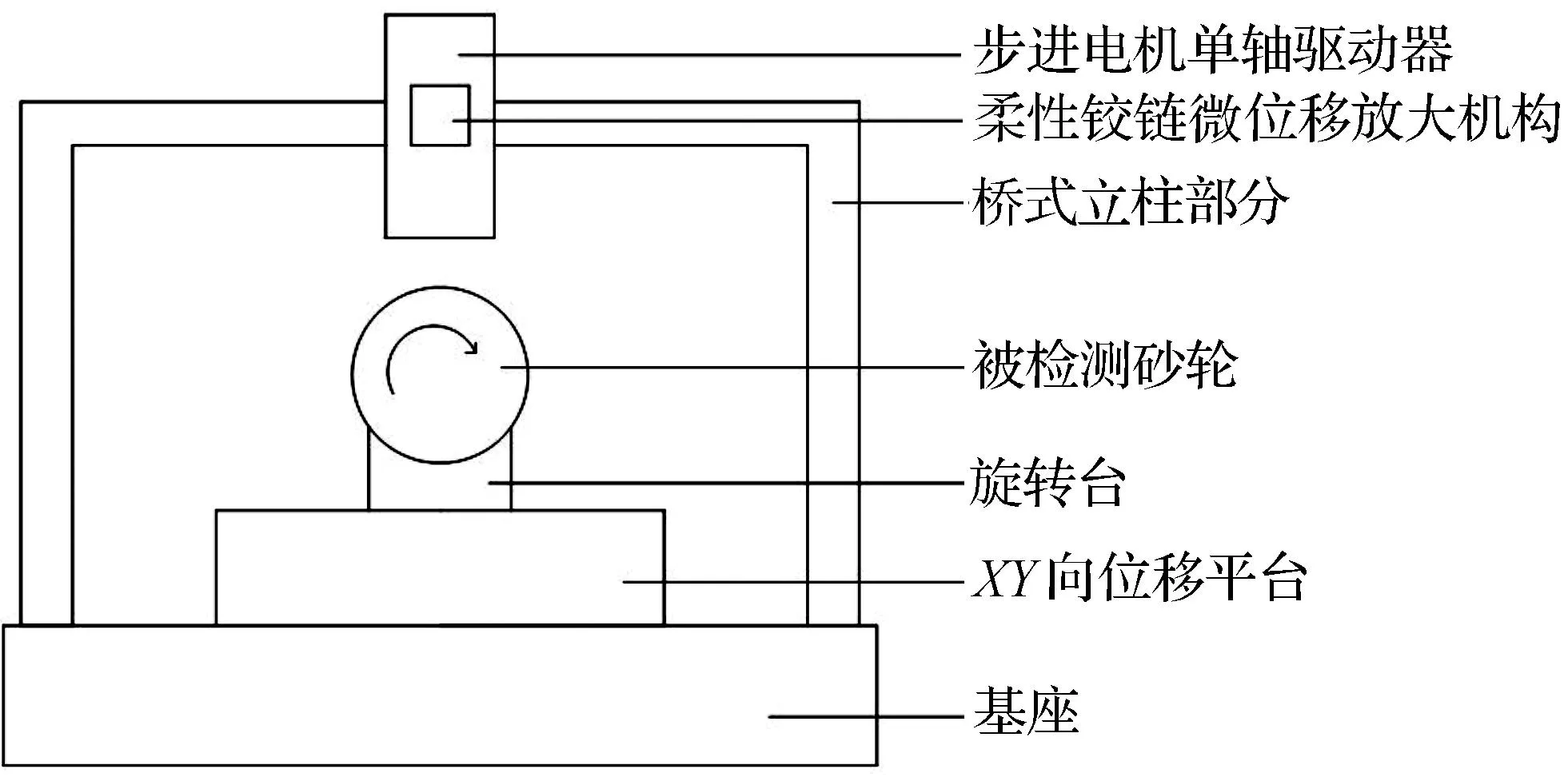
图1　三维运动机台结构示意图Fig. 1　Sketch of 3D displacement machine station

砂轮承载台包括XY向位移平台以及旋转台、砂轮定位夹具；立柱部分包括桥式立柱部分以及带有柔性铰链精级位移部分.其中旋转台绕垂直图1纸面轴线旋转，可以在图像采集时设定角度使砂轮旋转，便于实现后续图像拼接与处理；XY向位移平台提供砂轮整体水平二维运动；垂直运动机构(Z向)，主要包含了步进电机单轴驱动器和压电陶瓷驱动器微位移放大机构以此实现垂直方向上的粗精级运动.

1.1　XY向位移平台

XY向位移平台采用层叠式设计，为方便加工及装配两层采用完全一致的结构设计.CATIA装配图如图2所示(为显示内部结构，此图不含载物平台).驱动方式采用乐创自动化所生产的DM368三相步进电机配合米思米机械所生产的BSSR1210-265型滚珠丝杠，轴径12 mm，螺距10 mm，行程为±50 mm，定位精度±0.05 mm.同时采用SSEL2BWM14-350型双滑块加宽型微型直线导轨，基本额定负载8 500 N.单层运动模块都装有RENISHAW公司的光栅计量组件，以及限位传感器，防止在驱动程序失效时滚珠丝杠超过行程，对整个系统造成机械损伤.

图2　XY向位移平台Catia装配图Fig. 2　Catia assembly diagram of X-Ydirection displacement station

1.2　旋转台及砂轮定位夹具

旋转位移台采用北京光学仪器厂MRS系列102型精密电控旋转台，台面直径100 mm，分辨率0.0002°，重复定位精度<0.005°，最大静转矩40 N·cm，最大中心负载50 kg，以满足后续图像拼接要求.如图3所示，该部分还包括了支撑支架及三爪卡盘机构，可以适应装夹内径在20~30 mm区间的砂轮.

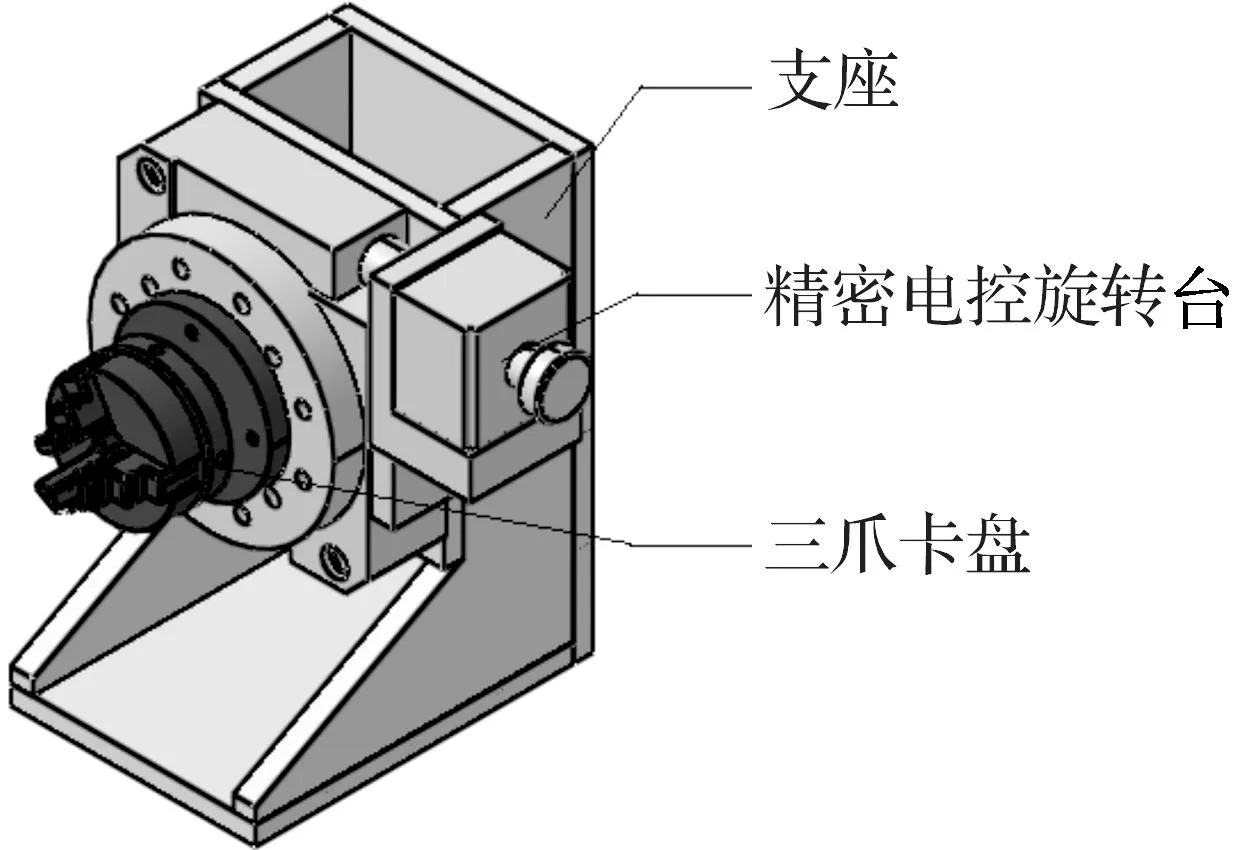
图3　砂轮承载平台Fig. 3　Stage for grinding wheel

2桥式立柱部分的设计与有限元分析

桥式立柱部分包含花岗岩材质的立柱以及金属材质的桥式横梁部分，这部分的主要作用是固定Z向位移机构及光学部件，包括镜头、CCD等.其CATIA模型如图4所示，底座及立柱部分采用大理石材质，因其具有刚性大、热膨胀系数小的特性，用来制作白光干涉仪工作平台底板基座及立柱，可以提供一个良好的参考面[5].底座部分尺寸为长770 mm，宽600 mm，高80 mm；立柱长150 mm，宽150mm，高400 mm.横梁部分采用金属材质，便于与Z向位移机构链接的同时也便于拆卸和功能扩展，如加装限位装置及计量光栅组件.

2.1　桥式立柱部分横梁的有限元分析

横梁部分采用四块平板通过螺栓连接固定而成，每块平板内部铣削有加强筋以提高横梁整体的静动力学性能.

2.1.1横梁静力学有限元分析

横梁由45号钢制成，其弹性模量为210 GPa，泊松比为0.3，密度为7.85 g/cm3.采用Abaqus对其进行静力分析，受中心载荷F作用，大小为20 N.为了方便网格划分，忽略了螺栓孔等小细节，可以减少计算时间以及增加网格的精度.如图5所示，分别是不含加强筋结构的板材以及含有方形和三角形结构的加强筋板材的三维模型，长770 mm,宽110 mm,厚20 mm.下面以方形加强筋板材为例，图6是方形加强筋板材受载后的Y向位移变形量云图，图7为合应力云图.

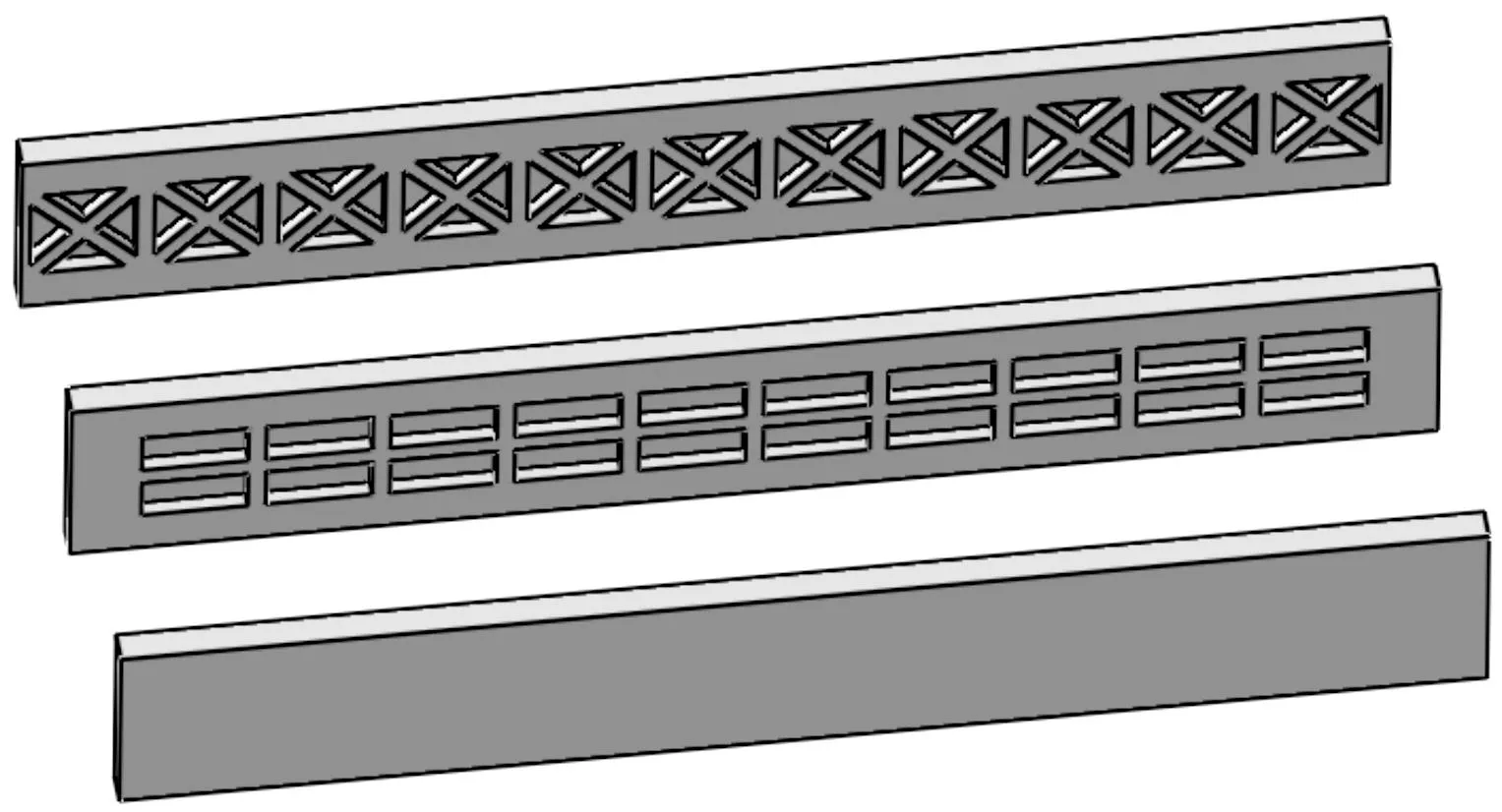
图5　板材三维模型Fig. 5　3D model of plates

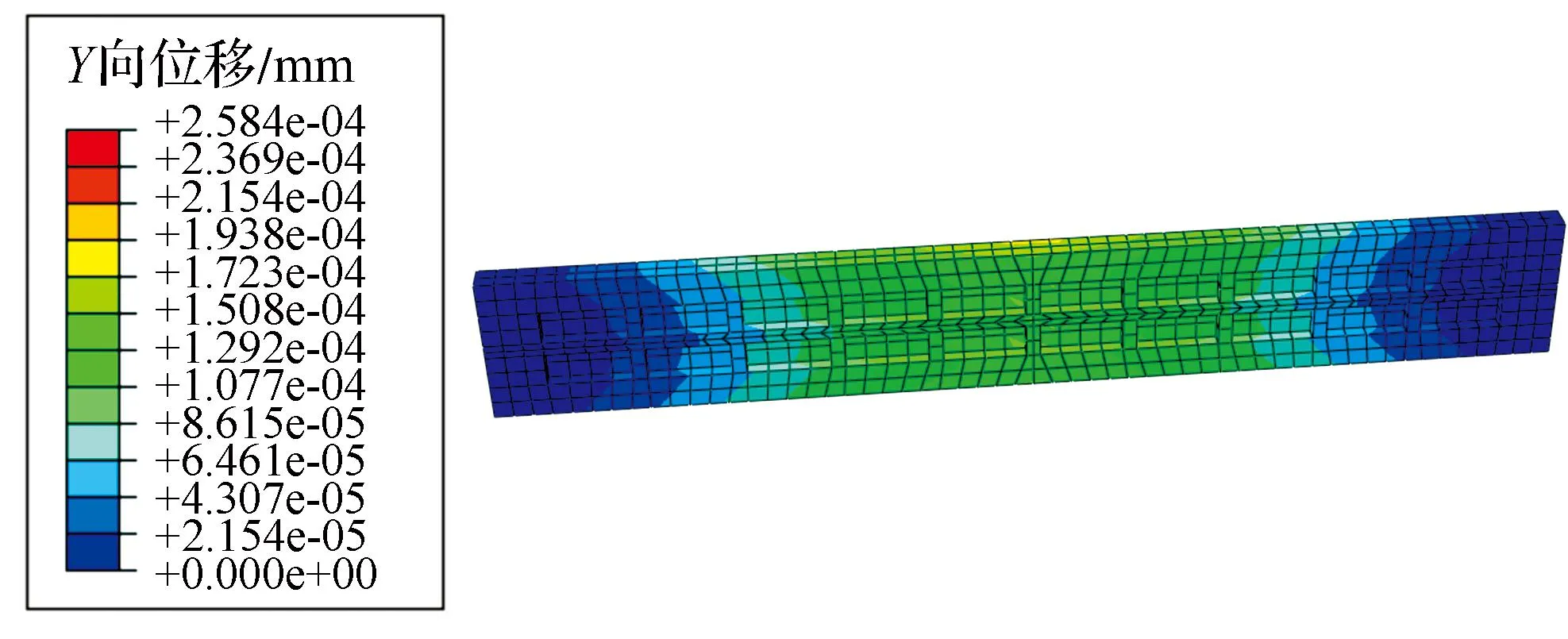
图6　方形加强筋板材Y向位移变形云图Fig. 6　Displacement deformation nephogram of Ydirection of plate with square stiffener

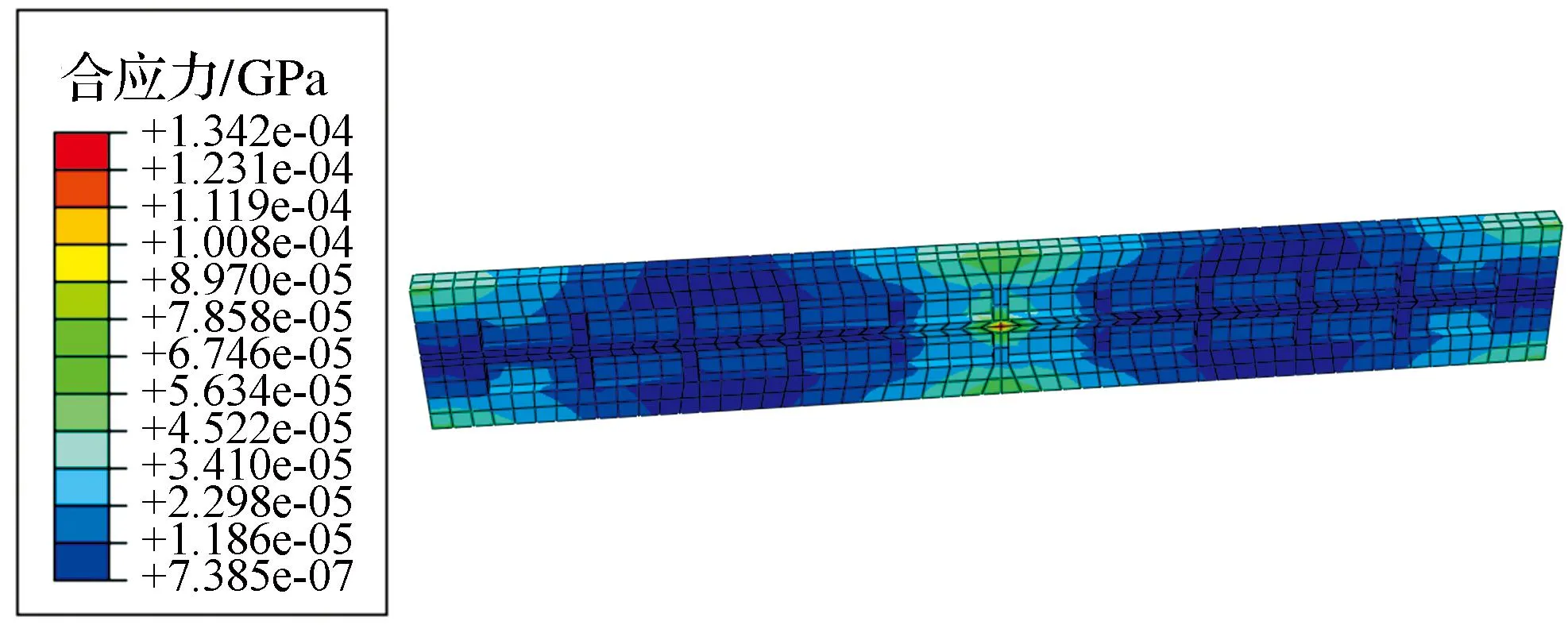
图7　方形加强筋板材合应力云图Fig. 7　Stress nephogram of plate with square stiffener

从静态分析结果可以得出，最大应力为0.13 MPa，远远小于材料的许用应力235 MPa，并且得到加载方向的最大位移为0.258 μm.同理可得无加强筋板材以及三角形加强筋板材的分析结果，如表1所示.

表1 三种板材静力学分析结果

从静力学分析可知，通过不断改变加强筋的尺寸并进行有限元分析考察其性能，可以显著提高板材的机械性能，含有方形加强筋的板材比无加强筋的板材在X方向上的位移减小了80.15%，Y方向上位移减少了76.69%，Z方向上减少了97.72%，最大应力增加了243%至0.134 MPa，质量减轻了17.71%；同理,带有三角形加强筋的板材比无加强筋的板材在X方向上位移减小了80.88%，Y方向上减少了78.59%，Z方向上减少了98.57%，最大应力增加了769%至0.339 MPa，质量减轻了13.65%.因为三者最大应力都远远小于材料的需用应力，所以最大应力虽然有巨大的增幅但这种影响可以忽略不计，相反通过合理布置加强筋的参数可以有效提高板材在XYZ三个方向的刚度，尤其是加载方向Y方向的刚度，并且可以显著减轻整个横梁结构的重量.

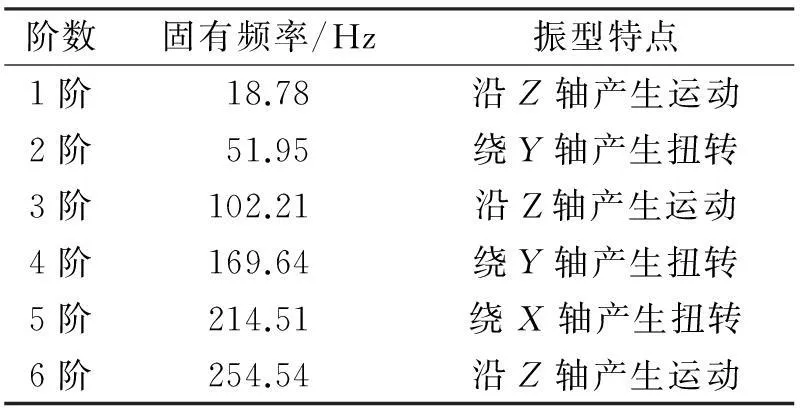
表2　无加强筋板材前6阶固有频率及振型

2.1.2横梁动力学有限元分析

考虑到光学检测系统中镜头对焦过程中镜头存在相对运动，故相当于加载在横梁的载荷是动态的，在分析中不能忽略结构的惯性，需引入动态分析.固有频率与振型是机械结构的固有特征，其数值应尽可能避开工作频率，以免发生共振效应，防止发生结构损伤[6].表2-表4分别为无加强筋结构、方形加强筋及三角形加强筋板材的前6阶固有频率及振型.

表3方形加强筋板材前6阶固有频率及振型

Tab. 3Six mode frequencies and mode shapes of

plate with square stiffener

阶数固有频率/Hz振型特点1阶153.31沿Z轴产生运动2阶241.09沿Y轴的运动及绕X轴的扭转3阶419.07绕Y轴的扭转4阶549.01绕Z轴的扭转5阶813.97沿Z轴产生的运动6阶957.05沿Y轴的运动及绕X轴的扭转

表4三角形加强筋板材前6阶固有频率及振型

Tab. 4Six mode frequencies and mode shapes of

plate with triangular stiffener

阶数固有频率/Hz振型特点1阶159.27沿Z轴产生的运动2阶436.00绕Y轴的扭转3阶605.26绕X轴的扭转4阶847.57沿Z轴产生的运动5阶889.97沿Y轴的运动及绕X轴的扭转6阶1236.60绕Z轴的扭转

可以看出，通过加入了方形或三角形加强筋可以使板材的1阶与2阶的固有频率有显著地提高，1阶固有频率分别从18.75 Hz上升到153.31 Hz以及18.75 Hz上升到159.27 Hz，2阶固有频率从51.95 Hz上升到241.09 Hz以及51.95 Hz上升到436 Hz.步进电机最高转速为1 500 r/min，即激振频率为25 Hz，而无加强筋的板材基频为18.78 Hz，小于激振频率，在实际使用过程中可能发生共振，而含有方形加强筋或三角形加强筋的基频大于激振频率，可以避免共振产生.故综合静、动力学分析结果将选用三角形加强筋板材来制作桥架立柱部分.

3垂直方向位移驱动部分

垂直运动方向具有粗、精两级运动，粗级运动机构采用米思米LX2605型单轴驱动器配合步进电机驱动，精级运动机构采用自行设计的柔性铰链放大机构配合压电陶瓷驱动器，以此来满足图像采集对焦过程对精密位移的需要,如图8所示.

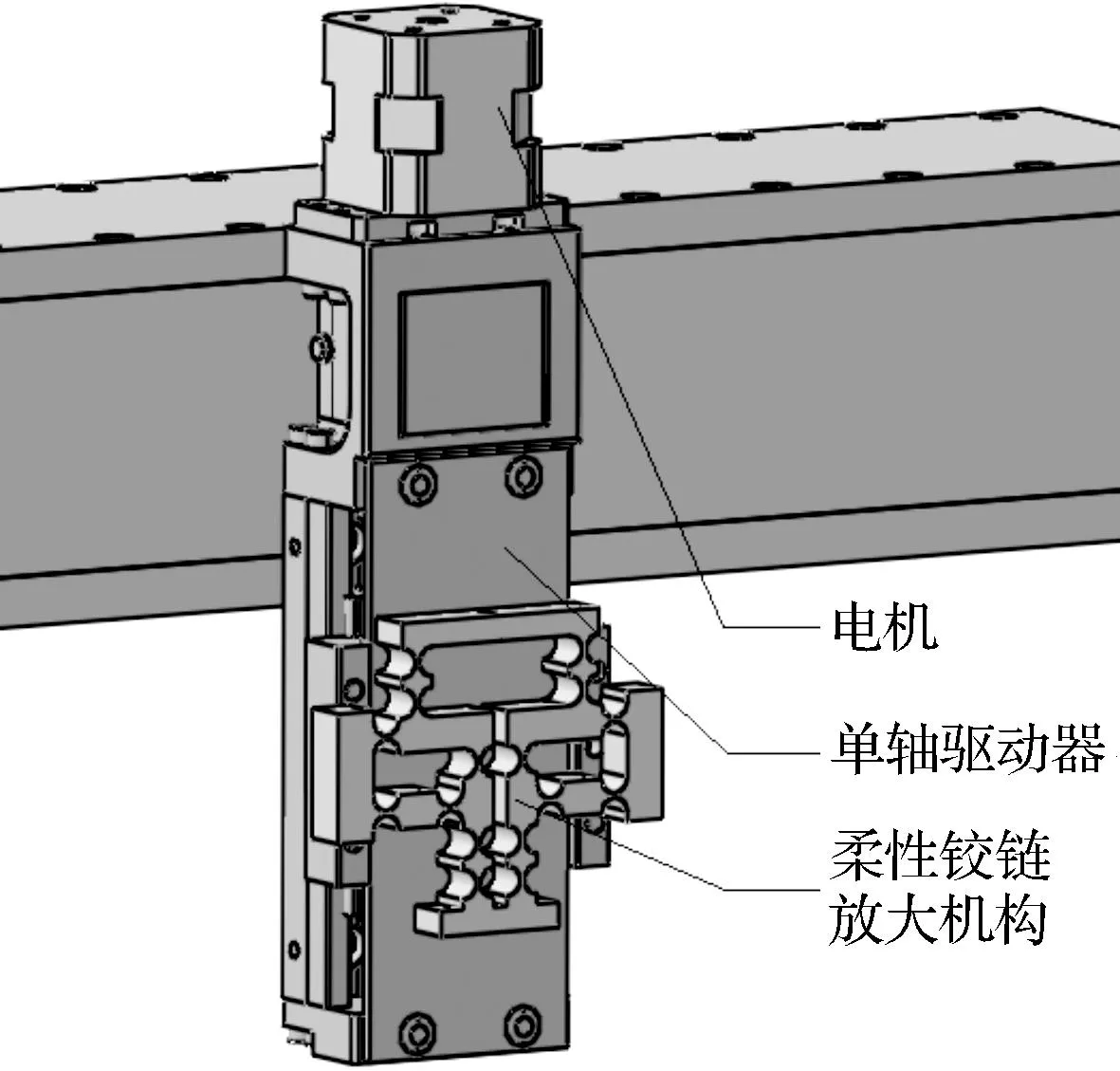
图8　单轴驱动器及柔性铰链Fig. 8　Single-axis driver and flexure hinge

3.1　直圆型柔性铰链单元

本文采用直圆型柔性铰链单元结构如图9，根据弹性静力学分析可得直圆型柔性铰链绕输出轴Z轴的转动刚度表达式[7]：

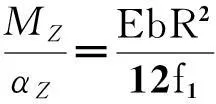
(1)

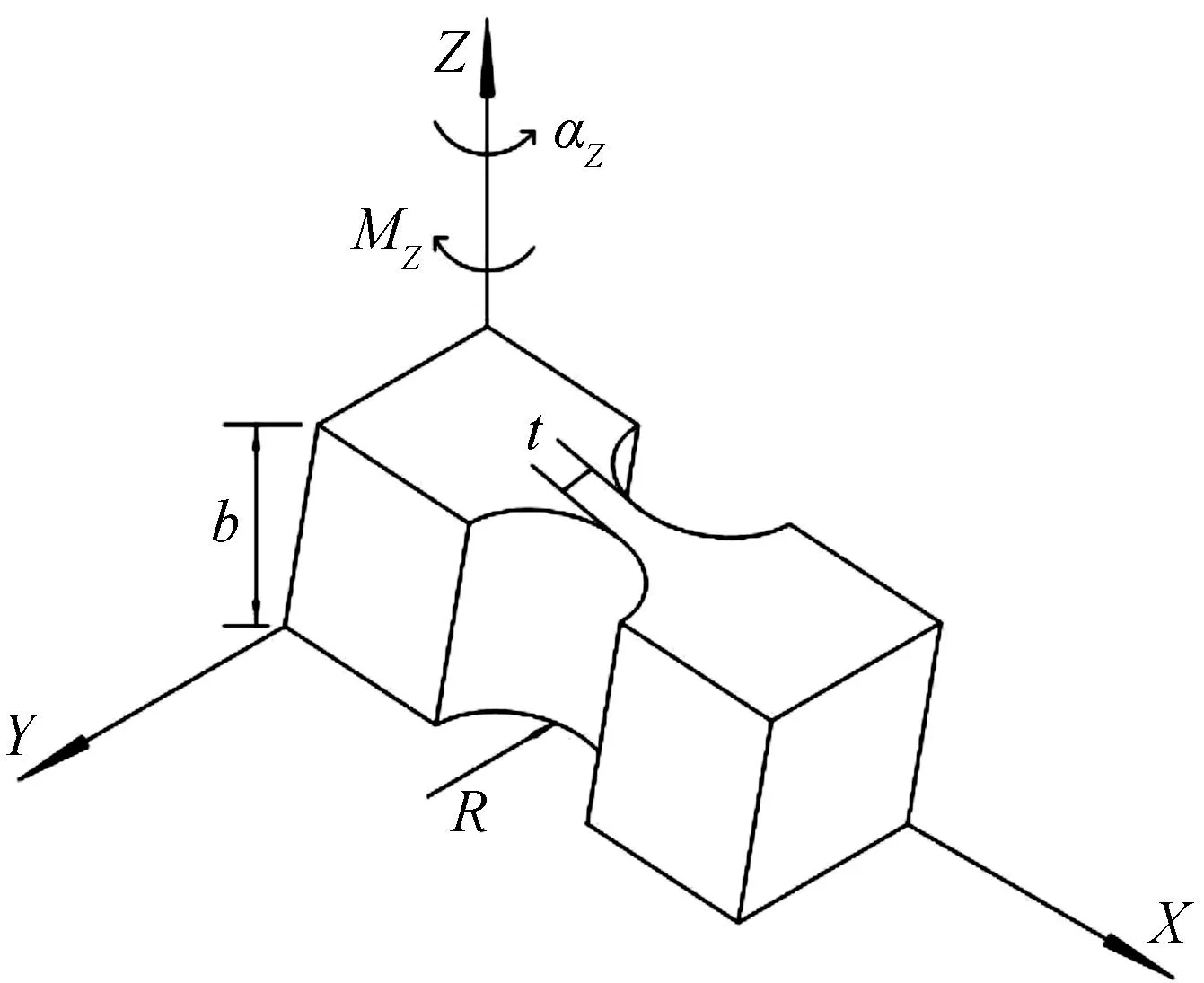
图9　直圆型柔性铰链单元Fig. 9　Right circular flexure hinge unit

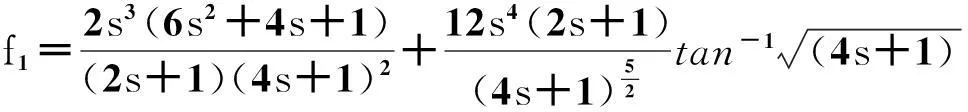
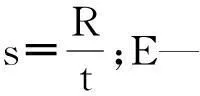
可见材料属性、切割半径R、厚度t以及铰链宽度b决定了直圆型柔性铰链单元的理论刚度，通过理论刚度计算与多次有限元仿真试验，综合考虑分析结果取切割半径R为3mm、最小厚度t为0.8mm、宽度b为10mm.

3.2　柔性铰链放大机构

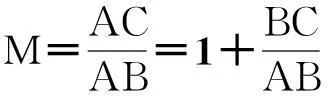
图10　柔性铰链放大机构简图Fig. 10　Structure sketch of micro-displacementmagnifying mechanism

3.3　微位移放大机构有限元分析

设置边界条件输入位移为15μm，负载为100N时微位移放大机构的Mises应力分布云图如图11所示，最大应力发生在柔性铰链单元最小厚度t处，最大应力为88.8MPa，65MN弹簧钢I类需用应力[σ]=340MPa，σmax<[σ]符合要求.相同边界条件下，理论得到输出端Y向位移28.1μm，可得有限元放大比1.87，与上文理论放大比基本一致，符合设计预期，同时得到输出端X向位移1.67e-10μm，相比于工作位移方向可忽略不计，即通过对称四杆机构可以消除附加位移，故按照图示尺寸进行加工.

图11　直圆型柔性铰链放大机构应力分布云图Fig.11　Stress nephogram of micro-displacementmagnifying mechanism

4结论

研究制作了一台砂轮用白光干涉仪三维运动机台.实现XY水平位移平台行程±50 mm，单脉冲步长实测0.3125 μm，电控旋转台分辨率为0.0002°，满足图像拼接对于砂轮旋转精度的要求.垂直运动方向，粗级运动机构步进电机单脉冲步长0.2 μm，行程为200 mm；精级机构行程15 μm，精度为0.03 μm，为后续进行砂轮的形貌测量、数据处理提供了功能完善的实验平台.

参考文献:

[1] 王生怀，陈育荣，王淑珍，等.三维精密位移系统的设计[J].光学精密工程，2010，18(1)：175-182.

[2] 高宏,李庆祥,严普强.亚微米弹性微位移工作台系统的设计及其精度分析[J].清华大学学报：自然科学版,1988,28(5):19-28.

[3] 王建林,刘文晖,胡晓东，等.压电微位移器在超微定位系统中的应用[J].压电与声光,1997,19(2):95-101.

[4] 言兰，融亦鸣，姜峰.氧化铝砂轮形貌的量化评价及数学建模[J].机械工学报，2011，47(17)：45-48.

[5] 范光照，朱志良，钟添东.小型微/纳米级三坐标测量机的研制[J].纳米技术与精密工程，2003，1(1)：18-23.

[6] 张向宇，熊计，郝锌，等.基于Ansys的立柱有限元分析与结构优化设计[J].机械科学与技术，2008，27(12)：1602-1605.

[7] 吴鹰飞，周兆英.柔性铰链的设计计算[J].工程力学，2002，19(6):136-140.

The Design of White-light Interferometer 3D Motion Machine for

Grinding Wheels Measurement

ZHONG Haoming, CUI Changcai, YU Qing

(College of Mechanical Engineering and Automation, Huaqiao University, Xiamen 361021, China)

Abstract:In order to predict and control the quality of the mechanical parts, the measurement, characterization and evaluation of the 3D profile of grinding wheels are critically important. This paper designs a white-light vertical scanning interferometer 3D motion machine for grinding wheels detection. It includes an X-Y direction displacement platform, a rotary location platform, bridge-shaped columns and a Z-direction micro-displacement system parts with flexure hinges. The platform structures are optimized by finite element static and dynamic analysis to satisfy the requirements. The single pulse length of X-Y direction displacement platform is 0.3125 μm. Z direction has a range of 15 μm with the accuracy of 0.03 μm.

Key words:white-light interferometer; finite element analysis; displacement platform