单隐含层模糊递归小波神经网络的观测器设计

闻新　李新　王尔申

(沈阳航空航天大学航空航天工程学部,沈阳 110136)



单隐含层模糊递归小波神经网络的观测器设计

闻新李新王尔申

(沈阳航空航天大学航空航天工程学部,沈阳 110136)

摘要根据模糊神经网络在非线性函数逼近方面的特性和小波变换具有良好的时频两维信号的分析能力,建立了结合两者优点的单隐含层模糊递归小波神经网络(Single hidden Layer Fuzzy Recurrent Wavelet Neural Network, SLFRWNN),并分析了SLFRWNN的结构、激活函数形式及激活函数对网络性能的影响.在此基础上,提出了一种基于SLFRWNN的自适应观测器设计方法,并通过引入Lyapunov函数,证明了这种观测器设计方法的稳定性,进而给出该网络观测器的初始化和最佳训练算法;仿真结果表明SLFRWNN观测器能很好地观测系统的状态.

关键词模糊神经网络;自适应观测器;非线性系统;仿真

资助项目: 国家自然科学基金(基金号：61571309,61101161)

联系人： 闻新 E-mail: wen_xin2004@126.com

引言

在复杂的系统工程中,系统存在诸多不确定因素和难以描述的非线性特性,为了解决这些问题,各种各样的观测器设计方法不断涌现,神经网络在处理非线性问题方面具有较强优势[1],所以利用神经网络为基础的状态观测器得到了迅速发展.相比传统的状态观测器,神经网络状态观测器具有较强的自适应性.

状态估计问题是由测得的输出量和整个状态变量不一致引起的[2].状态观测器通常是重构一个动态系统的状态,并在反馈控制、系统监控、故障检测和故障诊断等方面有着非常重要的应用.非线性系统的观测器设计已在过去几十年得到了广泛的应用[3],如张正强等[4]对具有未建模动态、未知参数、外部干扰的一类多输入多输出非线性系统构造了观测器,Musavi 等[5]利用低成本的微型电子机械系统(Micro-Electro-Mechanical System, MEMS)传感器设计了自适应模糊神经网络观测器应用于GPS系统,为了解决诸如系统模型不确定、多重时间延迟状态的不确定性和外部干扰等问题，文雄宇等[6]利用自适应小波神经网络观测器的跟踪控制方案对机器人的运行状态进行了全面的分析.贾鹤鸣等[7]使用神经网络状态观测器设计了一种吊重防摇晃的控制系统.但在设计或构造神经网络状态观测器时,必须遵守一些限定性条件,如要求非线性系统的状态完全可观等,因此对于复杂的非线性动态系统的观测器设计面临许多复杂的计算问题.因为神经网络在学习过程中存在收敛速率慢等问题,所以用神经网络设计非线性系统观测器的研究还有待进一步完善[8-14].

单隐含层模糊递归小波神经网络(Single hidden Layer Fuzzy Recurrent Wavelet Neural Netnork, SLFRWNN)具有较强的泛化能力,因此它能够以较高的精度实现函数逼近和系统辨识.本文提出了一种基于SLFRWNN的自适应状态观测器设计方法,并应用于非线性系统进行数值仿真验证.

1单隐含层模糊递归小波神经网络

具有5层神经元的SLFRWNN其模型如图1所示,其中隐含层使用小波函数作为激活函数.隐含层神经元是一种记忆单元,它存储了隐含层神经元上一步的输出,下个时间步时便把记忆的输出乘以一个反馈增益后再输入到隐含层.正是这种递归记忆的特性,才使该网络具有动态逼近非线性的性能.

图1　单隐含层模糊递归小波神经网络模型

图1中,网络第二层的输入隶属度函数μAIJ(xi)和每个节点的输出通过式(1)计算:

∀ i=1∶Nin; j=1∶Nr.

(1)

式中: cij表示隶属度函数中心; σij表示隶属度函数宽度.

第三层的每个节点表示模糊规则R,其输出用式(2)表示

j=1∶Nrand0<μj≤1.

(2)

第四层是网络的单隐含层,其小波函数作为激活函数见表1所示.

1) 高斯小波函数具有全局映射泛化能力,而且在细化局部方面也有效果,已有多种类型网络使用该函数作为激活函数,网络收敛速度不仅快,还能避免过拟合现象.

2) 墨西哥草帽函数是高斯函数的二阶导数,它没有尺度函数及不具正交性,但它具有对称性和指数衰减性,时频域具有良好的局部化能力.该函数作为网络激活函数时,网络收敛较快,但无法避免陷入局部极小值的缺点.

3)Morlet小波函数是一种复值小波函数,尺度函数不存在且不具有正交性,该函数作为网络激活函数时,网络收敛较前两者慢,但模型过低的自由度会导致欠拟合现象.

表1　小波函数

选择高斯小波函数作为激活函数,则第四层的每个小波φij为

φijφij(zij(k))=(μij(k)-tij(k))/dij(k),

∀i=1∶Nin, j=1∶Nr.

(3)

在离散时间k时,

μij(k)=xi(k)+φij(k-1)·θij(k),

i=1∶Nin, j=1∶Nr.

(4)

式中: tij和dij分别表示小波平移系数和伸缩系数; θij为反馈增益,类似于存储系数.

则第四层的子小波函数计算为

∀ j=1∶Nr.

(5)

相应的输出为

υj(k)=wj·Ψj, j=1∶Nr.

(6)

第四层与第三层的节点输出相乘,结果为

(7)

式中:

(8)

第五层为网络的输出层,其输出为

(9)

2基于SLFRWNN的自适应观测器设计

2.1　观测器设计

考虑如下非线性系统:

(10)

式中: x(t)∈Rn为状态变量; u(t)∈Rq为输入变量;f(x(t),u(t))为非线性函数向量; A∈Rn×n为定常矩阵;在输出方程中y(t)∈Rm为输出变量; C∈Rm×m为定常矩阵; (A, C)是可观测的矩阵对.

针对式(10)的非线性系统,构造图2所示的SLFRWNN观测器模型.

图2　基于SLFRWNN的状态观测器结构图

式(10)非线性系统的状态观测器描述为

(11)

式中: G为观测器的增益矩阵,满足M=A-GC为渐进稳定的Hurwitz矩阵.

假设SLFRWNN的输入输出之间的关系为y(t)=WTg(x(t)),给定逼近误差ε(x(t)),根据神经网络具有逼近任意非线性系统的性能,则存在εi(x(t))∈ε(x(t))>0使得SLFRWNN能够逼近非线性函数f(x(t),u(t)),表示如下:

ζ(x(t))=Wg(x(t))+εi(x(t)).

(12)

式中:f(·)是使用高斯小波函数作为激活函数; W为隐含层的权值矩阵,满足‖εi(x(t))‖≤εN,εN是它的边界函数,并由隐含层神经元决定.在这里假设权值矩阵W有界,且有‖W‖F≤WM.

根据神经网络的逼近性能,利用f(x(t),u(t))来替代ζ(x(t)),式(12)变为

f(x(t),u(t))=Wg(x(t),u(t))+

εi(x(t)).

(13)

因此,网络函数估计为

(14)

将式(14)带入式(11)得

(15)

定义状态误差e(t)和输出误差ey(t)为

(16)

由式(10)、(15)、(16)可得误差动态方程为

(17)

2.2　稳定性分析

在一定的条件下定义一个合适的学习规则,能更好地训练神经网络,这就需要保障观测器的稳定性.要使观测器保持稳定性,一般采用权值校正准则,并引入Lyapunov函数证明权值误差的有界性.为了更简洁地证明本文所设观测器的稳定性,将式(17)进行如下简化

(18)

式中:

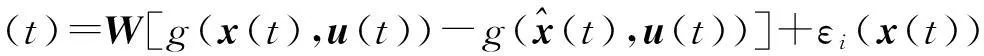
根据文献[15]对神经网络权值进行修正，有

(19)

将式(18)进行求解得

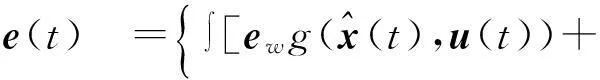
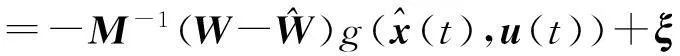
(20)

则

(21)

将式(20)和式(21)代入式(19)得到修正后的神经网络权值为

(22)

(23)

引入正定的Lyapunov函数[16]为

(24)

式中: P=PT>0为正定矩阵,且对任意正定矩阵Q满足

MTP+MPT=-Q.

(25)

将式(24)求导可得

(26)

将式(18)、(23)、(25)代入式(26)得

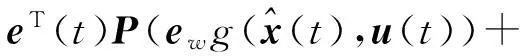
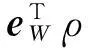
(27)

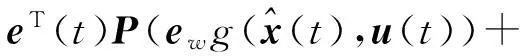
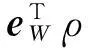
(28)

根据下列不等式组

(29)

可得

‖δ‖+ρ‖Ce(t)‖·(WM‖eW‖-

‖eW‖2).

(30)

式中:λmin(Q)为矩阵Q的最小特征值;WM=sup(W);gM=sup(g).进一步整理得

‖eW‖(gM‖δ‖+ρWM‖C‖)].

(31)

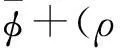
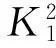
(32)

此外,为了表示权值误差的界限,式(23)可表示为

ρ‖ey(t)‖W-ρ‖ey(t)‖eW.

(33)

2.3　基于SLFRWNN观测器的初始化

由于BP神经网络的收敛速度取决于初始值的选择,使用GA对SLFRWNN进行初始化.假设有Ns个样本(x(1),x(2),…，x(k),…，x(Ns)),时间为0到t.SLFRWNN初始化就是基于期望值和网络输出值之间误差的最小化.设yd(k)为期望输出,yq(k)为实际输出,因此,在样本为k时,第q个核函数计算为

(34)

式中

∀i=1∶Nin,j=1∶Nr，

(35)

(36)

用向量表示为

∀i=1∶Nin,j=1∶Nr.

(37)

式中:

在种群中,用GA在解空间中进行全局搜索,则相应最小适应度函数值的最优解取决于网络参数的初始值[17].

2.4　基于SLFRWNN观测器的最佳训练算法

在神经网络训练的过程中,模糊准则后件的所有参数需要进行自动调整,本文使用反向传播算法对后件参数进行调整.令yd(k)和y(k)分别为网络在离散时间k时的期望输出和实际输出,则k时刻的网络误差为

e(k)=yd(k)-y(k).

(38)

取代价函数

(39)

设网络从时间步1工作到时间步Nr,则每个周期的总误差函数为

(40)

后件参数wj、tij、dij和θij使用式(41)～(44)进行调整:

(41)

(42)

(43)

(44)

式中:γ=[γw,γt,γd,γθ]表示学习速率,即0<γ<1.式(41)～(44)的偏导数值为

=(y(k)-yd(k))·

(45)

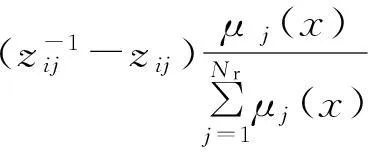
(46)

(47)

(48)

式(36)和式(45)～(48)均使用高斯小波函数作为小波母函数.

3系统仿真

考虑如下非线性系统,状态方程如式(10),其对应参数值如下：

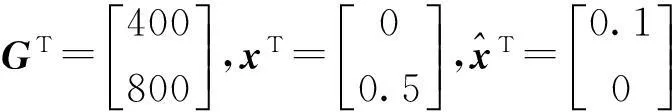
图3　x1的状态估计曲线以及估计误差

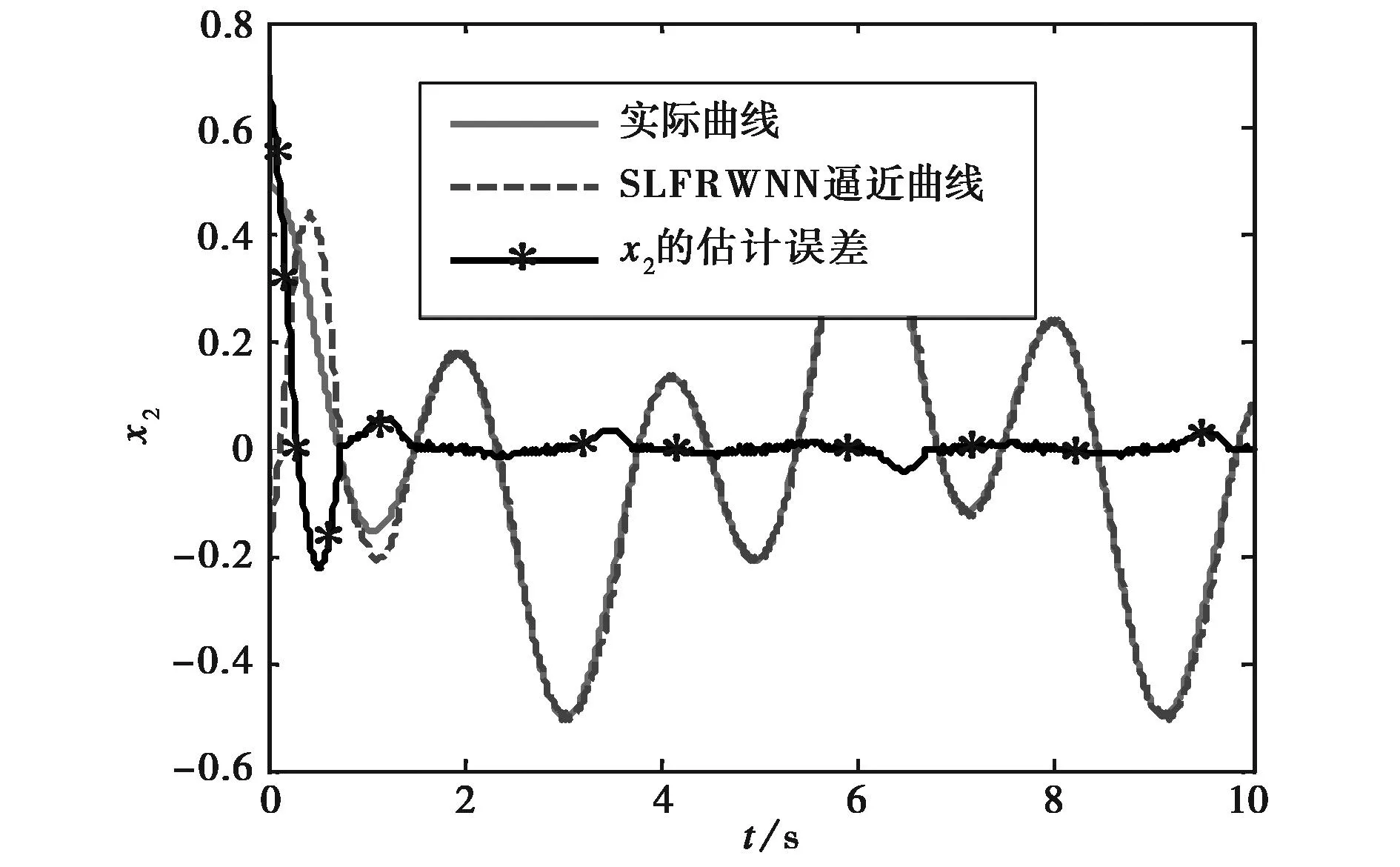
图4　x2的状态估计曲线以及估计误差

由图3和图4的仿真曲线可以看出,SLFRWNN自适应观测器对非线性系统的状态变量具有很好的跟踪能力.图4在开始阶段的逼近效果不是很好,这主要是由于状态变量进行初始化时,初始值的选取是按照经验进行选取,从而造成开始阶段的估计误差相对较大.图4中状态误差有微小的波动,主要是由状态变量存在轻微的震荡引起的,震荡周期大约为1ms.从图5可以看出,在刚开始阶段,SLFRWNN的跟踪估计误差相对较大,但随着时间的推移,误差值越来越小,其SLFRWNN平均估计误差为0.041,这归结为高斯函数作用的结果.图3和图4的仿真结果最终表明,该自适应观测器可以克服微小的波动,从而实现系统状态的快速跟踪.

图5　输出y的相对误差

4结论

本文建立了5层单隐含层模糊递归小波神经网络,该网络后件具有较少的神经元,并能有效地跟踪快速变化的过程,并在此基础上使用该神经网络设计了一种新的自适应观测器.仿真结果表明,该自适应观测器能够快速有效的跟踪状态参数的变化,并对非线性动态神经系统具有很好的自适应逼近能力.但是,由于神经网络自身的缺陷,如网络训练时间长、迭代次数多、优化的参数多等,这些问题有待于进一步的完善.

参考文献

[1]李江曼, 赵振维, 郭立新, 等. 地基微波辐射计分段正交神经网络方法遥感阴天大气[J]. 电波科学学报, 2014, 29(6): 1105-1109.

LIJiangman,ZHAOZhenwei,GUOLixin,etal.Asubsectionorthogonalneuralnetworktechniquefortheground-basedradiometertoremotelysensecloudyatmosphere[J].ChineseJournalofRadioScience, 2014, 29(6): 1105-1109. (inChinese)

[2]BESANCONG.Nonlinearobserversandapplications,in:lecturenotesincontrolandinformationsciences[M].Berlin:Springer-Verlag, 2007.

[3]EKRAMIANM,SHEIKHOLESLAMF,HOSSEINNIAS,etal.AdaptivestateobserverforLipschitznonlinearsystems[J].Systems&ControlLetters, 2013,62(4):319-323.

[4]ZHANGZhengqiang,XUShengyuan.Observerdesignforuncertainnonlinearsystemswithunmodeleddynamics[J].Automatica, 2014, 50(1): 80-84.

[5]MUSAVIN,KEIGHOBADIJ.Adaptivefuzzyneuro-observerappliedtolowcostINS/GPS[J].AppliedSoftComputing, 2015, 29(1): 82-94.

[6]YUWS,WENGCC.Anobserver-basedadaptiveneuralnetworktrackingcontrolofroboticsystems[J].AppliedSoftComputing, 2013, 13(12): 4645-4658.

[7] 贾鹤鸣, 张利军, 齐雪. 基于神经网络的水下机器人三维航迹跟踪控制[J]. 控制理论与应用, 2012, 29(7): 877-883.

JIAHeming,ZHANGLijun,QIXue.Three-dimensionalpathtrackingcontrolforautonomousunderwatervehiclebasedonneuralnetwork[J].ControlTheoryandApplications, 2012, 29(7): 877-883. (inChinese)

[8] 嵇艳鞠, 徐江, 吴琼, 等. 基于神经网络电性源半航空视电阻率反演研究[J]. 电波科学学报, 2014, 29(5): 973-980.

JIYanju,XUJiang,WUQiong,etal.Apparentresistivityinversionofelectricalsourcesemi-airborneelectromagneticdatabasedonneuralnetwork[J].ChineseJournalofradioScience, 2104, 29(5): 973-980. (inChinese)

[9]YANGDongsheng,LIUXinrui,XUYukun,etal.Stateestimationofrecurrentneuralnetworkswithintervaltime-varyingdelay:animproveddelay-dependentapproach[J].NeuralComputAppl, 2013, 23(3): 1149-1158.

[10]SCHWENKERF,KESTLERHG.Threelearningphasesforradialbasisfunctionnetworks[J].NeuralNetworks, 2001, 14(2): 439-458.

[11]CHENGCaixia,SUNFuchun,ZHOUXinquan.Onefiredetectionmethodusingneuralnetworks[J].TsinghuaScienceandTechnology, 2011, 16(1): 31-35

[12]ADHYARUDM.Stateobserverdesignfornonlinearsystemsusingneuralnetwork[J].AppliedSoftComputing, 2012, 12(8): 2530-2537.

[13]曹海青, 王渝, 杜明芳, 等. 小型漂浮式卫星天线自抗扰控制器的研究[J]. 电波科学学报, 2014, 29(5): 841-847.

CAOHaiqing,WANGYu,DUMingfang,etal.Activedisturbancerejectioncontrollerforsmall-sizedfloatantenna[J].ChineseJournalofRadioScience, 2014, 29(5): 841-847. (inChinese)

[14]GRIPHF,SABERIA,JOHANSENTA.Observersforinterconnectednonlinearandlinearsystems[J].Automatica, 2012, 48(7): 1339-1346.

[15]SHAIKFA,PURWARS,PRATAPB.Real-timeimplementationofChebyshevneuralnetworkobserverfortwinrotorcontrolsystem[J].ExpertSystemswithApplications, 2011, 38(10): 13043-13049.

[16]ABDOLLAHIF,TALEBIHA.Astableneuralnetworkobserver-basedobserverwithapplicationtoflexiblejointmanipulators[J].IEEETransactiononNeuralNetwork, 2006, 17(1):118-129.

[17]TOFIGHIM,ALIZADEHM,GANJEFARS,etal.Directadaptivepowersystemstabilizerdesignusingfuzzywaveletneuralnetworkwithself-recurrentconsequentpart[J].AppliedSoftComputing, 2015, 28(3):514-526.

闻新(1961-),男,辽宁人,沈阳航空航天大学博士生导师,南京航空航天大学航天控制系主任,主要研究的方向为航天器总体设计与故障诊断．

李新 (1988-),男,江苏人,沈阳航空航天大学航空航天工程学部硕士研究生,主要研究方向为智能检测与诊断及航天器故障诊断技术．

王尔申(1980-),男,辽宁人,博士,副教授,在站博士后,主要研究方向为卫星导航、智能信号处理．

张忠祥, 孔勐, 陈明生, 等. 一种计算复杂天线散射截面的新型快速方法[J]. 电波科学学报,2015,30(6):1205-1210. doi: 10.13443/j.cjors. 2014103003

ZHANG Zhongxiang, KONG Meng, CHEN Mingsheng, et al. A novel method of RCS fast calculation with complex antenna structure[J]. Chinese Journal of Radio Science,2015,30(6):1205-1210. (in Chinese). doi: 10.13443/j.cjors. 2014103003

Observer design for the single hidden layer fuzzy

recurrent wavelet neural network

WEN XinLI XinWANG Ershen

(FacultyofAerospaceEngineering,ShenyangAerospaceUniversity,Shenyang110136,China)

AbstractThe fuzzy neural network has good nonlinear function approximation properties, and wavelet transform has good time-frequency signal analysis capabilities. The single hidden layer fuzzy recurrent wavelet neural network (SLFRWNN) is developed by combining with the advantages of both in this paper. The structure of networks, the form of its activation functions and its influence on SLFRWNN are analyzed. Then a design method of adaptive observer based on the single hidden layer recurrent fuzzy wavelet neural network is proposed. The Lyapunov function is introduced to prove the stability of this observer design method. And the network observer of initialization and the optimal learning algorithm is given. The final simulation results show that the single hidden layer neural fuzzy recurrent wavelet network observer can easily observe the state of the system.

Key wordsfuzzy neural networks; adaptive observer; nonlinear systems; simulation

作者简介

收稿日期：2014-10-14

中图分类号TP183

文献标志码A

文章编号1005-0388(2015)06-1197-08