迭代傅里叶算法用于六边形稀疏阵列天线
2015-02-24刘恒刘波谢广钱赵宏伟
刘恒 刘波 谢广钱 赵宏伟
(中国空间技术研究院西安分院,西安 710100)
迭代傅里叶算法用于六边形稀疏阵列天线
刘恒刘波谢广钱赵宏伟
(中国空间技术研究院西安分院,西安 710100)
摘要针对迭代傅里叶技术在优化稀疏阵列天线时对阵元激励大规模截断带来的不利影响,提出了一种逐步截断的迭代傅里叶算法.该算法从满阵依次减少数个阵元,从而避免阵列大规模截断陷入局部最优解.将其应用到六边形平面天线阵列的稀疏布阵优化中,以改善最大副瓣电平为目的.为了计算六边形天线阵的方向图,通过在口径中添加虚拟阵元转化为可以实现二维傅里叶变换的矩形阵列.仿真结果表明,改进的迭代傅里叶算法对稀疏天线阵最大旁瓣电平的优化比采用遗传算法的结果更理想,且具有计算量小和速度快等优点.
关键词阵列天线;稀疏阵列;迭代傅里叶算法;副瓣电平
资助项目: 国家自然科学基金(61201089); 国防重点实验室基金(9140C530101130C53013)
联系人: 刘恒 E-mail:liuheng@mail.nankai.edu.cn
引言
稀疏阵列天线是指从一个阵元周期分布的阵列中去除掉一些天线阵元,或者把这些阵元连接到匹配负载上.既可以减少阵列天线成本和重量,还可以获得与满阵排布相当的窄波束,当阵元等幅激励时,稀疏阵列天线可以获得比满阵布置更低的副瓣电平.20世纪80年代,稀疏阵列天线已经在ESAR、HAPDAR、SBX等雷达系统中成功应用;目前,在卫星抗干扰的接收天线,高频地面雷达天线和射电天文学中的干涉阵列等领域得到了越来越广泛的应用.
随着计算机的迅速发展,高效率的阵列天线稀疏优化技术已成为研究热点,有遗传算法[1-2]、粒子群算法[3-4]、进化差分算法[5-6]等各种智能进化算法,这些随机搜索的进化算法往往需要长时间的进化运算才能达到工程满意解.阵列天线稀疏优化是一个多极值问题,对于大型阵列天线,其搜索空间极大,由于计算机资源的限制和智能算法的随机搜索本质,所得到的可能是工程不满意解.2007年,荷兰物理学家Keizer提出了迭代傅里叶技术(Iterative Fourier Technique, IFT),并把它应用于均匀激励的直线[7]和平面[8-9]稀疏阵列方向图综合,取得了比传统智能优化算法更低的最大副瓣电平(Maximum SideLobe Level, MSLL),且IFT还具有程序设计简单、收敛速度极快的优点.由于在同等间距同等阵列口径面积下,三角栅格阵列可以比矩形栅格阵列排布更多的阵元,近似圆形的六边形平面阵列在均匀激励时能够获得相对低的副瓣电平,在扫描时出现栅瓣的扫描角度更大,因此六边形天线阵被广泛应用在通信和雷达中[9].目前国内外公开发表的文献,应用IFT算法都是在对直线阵和矩形平面阵[10-11]进行稀疏布阵优化,未见文献报道使用IFT算法对六边形平面阵列天线进行稀疏布阵优化方面的工作.
在标准IFT的迭代过程中,通过调整远场方向图和口径阵元的激励,分别对它们做正向快速傅里叶变换(Fast Fourier Transform, FFT)和逆向快速傅里叶变换(Inverse Fast Fourier Transform, IFFT)来优化阵列的辐射特性.在阵列方向图施加IFFT获得阵元激励后,将其中具有较小激励值的阵元一次性设为“关”状态,容易使所得的解陷入局部最优解.本文提出一种改进IFT算法,从满阵开始迭代,每次对阵因子作IFFT获得阵元激励后,依次增加数个处于“关”状态的阵元,从而避免了对阵元激励大规模一次性截断带来局部收敛的不足.为了对六边形平面阵列的辐射问题进行了理论分析,通过添加虚拟阵元把六边形阵列转化为矩形阵列,把六边形阵的阵元激励与阵因子通过二维FFT联系起来.然后将改进的IFT算法应用于1 027个阵元的六边形平面阵列,进行稀疏优化以降低阵列天线的最大副瓣电平,并得到了满意的结果,说明了此方法在工程应用中的有效性和可行性.
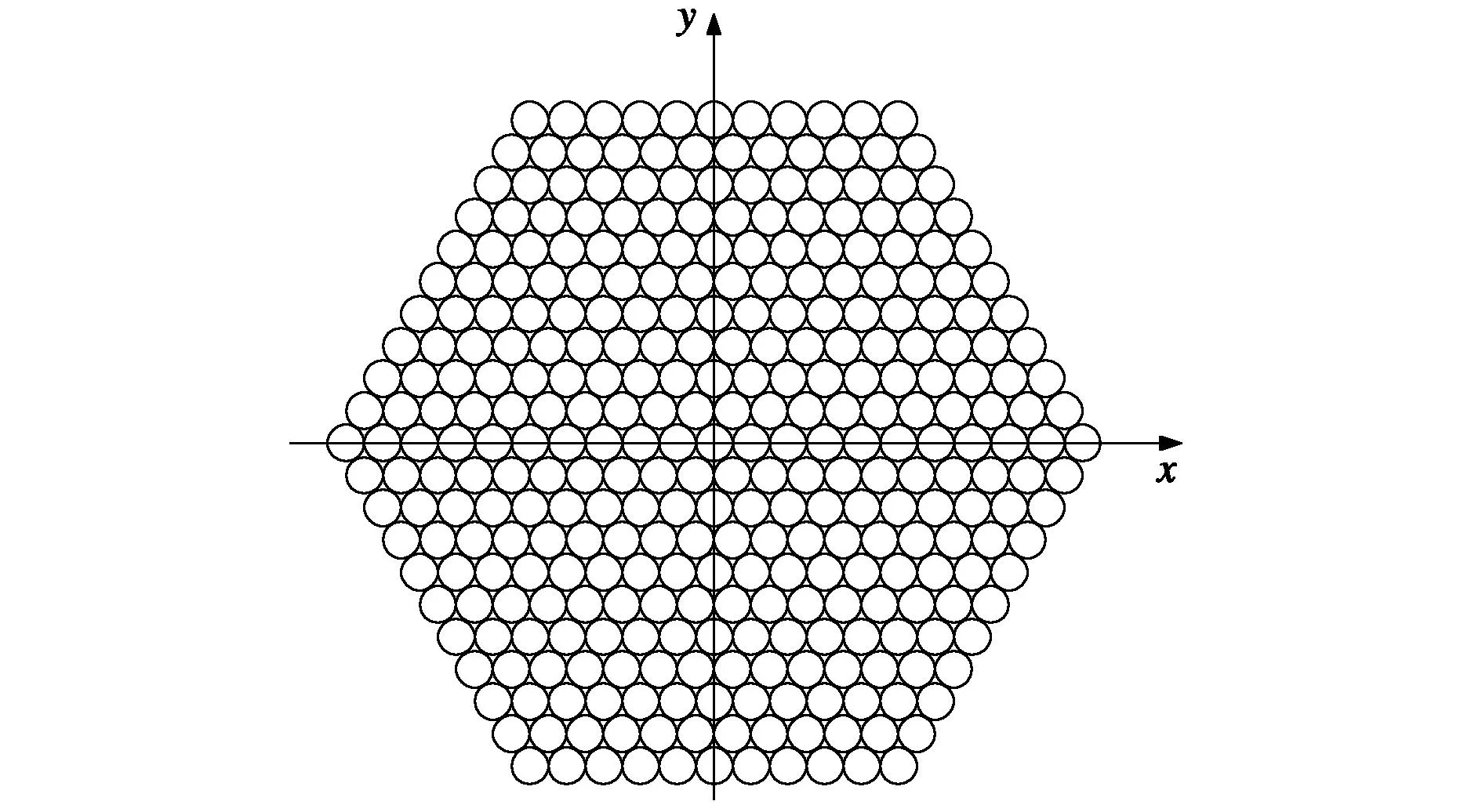
图1 六边形平面阵列天线结构图
1六边形阵列天线方向图
六边形天线阵列的几何结构如图1所示,它由按等边三角形排列的天线单元组成.可以看出六边形平面天线阵是由若干行横向等间距的直线阵在纵向交替紧密排布组成,其每行的单元数量随着远离中心行依次递减.对于一个由L个同心六边形环阵组成的六边形平面天线,其第一行的阵元数为L+1个;随着行数的增加,每行的阵元数依次增一个,到L+1行的阵元数增加到最多的2L+1个;再随着行数继续增加,每行的阵元数则依次减少一个,到2L+1行的阵元数减少到L+1个.下面将利用六边形平面天线阵的这一结构特性推导它的辐射方向图的解析表达式.
由于六边形平面阵列的每行在y方向是交替排布的,如果通过在每行的阵元中间添加一个虚拟的“阵元”,这样就把六边形平面阵列变换为矩形栅格的平面阵列.每行沿x轴方向间距dx=0.5d,每列沿y轴方向间距dy=0.5d·tan60°,d为正三角形排列的阵元间距.根据六边形平面阵列的结构和添加的虚拟阵元的位置可知,对于一个由L个同心六边形环阵通过在每一行单元中间添加虚拟阵元变化为一个2L+1行4L+1列的矩形栅格平面阵.由阵列天线理论可知,在不考虑互耦的情况下,辐射阵元为理想点源,六边形阵列方向图满足乘积定理可以表示为
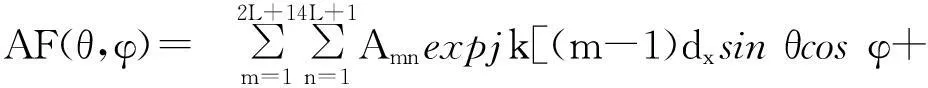
(n-1)dysinθsinφ].
(1)
式中: L为同心六边形环阵的数量; k为波数; θ,φ分别为球坐标系的下俯仰角和方位角; Amn是第(m,n)个阵元激励幅度.为了方便,把由M×N个阵元激励组成的矩阵记着A,对于矩阵A与六边形平面阵列不匹配的点,如添加的虚拟阵元和位于六边形阵列孔径外的点,其激励幅度Amn=0.对于与阵列匹配的点,在稀疏优化过程中,当Amn=1,表示单元在工作;当Amn=0,表示单元被剔除.六边形天线阵列(含有L个同心六边形环阵)的满阵单元数可由下式得到:
(2)
2IFT算法描述
2.1 阵列方向图与FFT的关系
一个辐射阵元为理想点源,沿x轴方向的阵元间距为dx,y轴方向的阵元间距为dy的M×N元平面阵,在不考虑互耦的情况下,阵列方向图满足乘积定理,可以表示为
(3)
式中:Amn是第(m,n)个阵元激励幅度,对于稀疏阵列,当Amn的取值为1,表示阵元处于“开”状态时,此时该位置的阵元连接到馈电网络;而当Amn的取值为0,表示阵元处于“关”状态时,此时阵元连接到匹配负载.k=2π/λ,λ为自由空间波长.u=sinθ
cosφ,v=sinθsinφ是方向余弦,θ,φ分别为球坐标系的下俯仰角和方位角.令p=Mkdxu/2π+1,q=Nkdyv/2π+1,则式(3)变换为
(4)
由式(4)可以看出阵因子F与阵元激励A之间存在IFFT关系F=MN×IFFT(A),这样根据具体的问题,将(θ,φ)域的方向图特性映射到(p,q)域中,就可以在(p,q)进行优化.
由u=sinθcosφ,v=sinθsinφ可得u2+v2=sin2θ≤1,在u,v坐标系下,可见区域与一圆区域相对应.对于不同间距的平面阵列,利用二维FFT计算出方向图的可见区域,如图2所示.当dx≤λ/2,dy≤λ/2时,可见区域为半径为1的圆A;当dx>λ/2,dy<λ/2时,可见区域为半径为1的圆与矩形D的交集;当dx<λ/2,dy>λ/2时,可见区域为半径为1的圆与矩形C的交集;当dx>λ/2,dy>λ/2时,可见区域为矩形C与矩形D的交集.
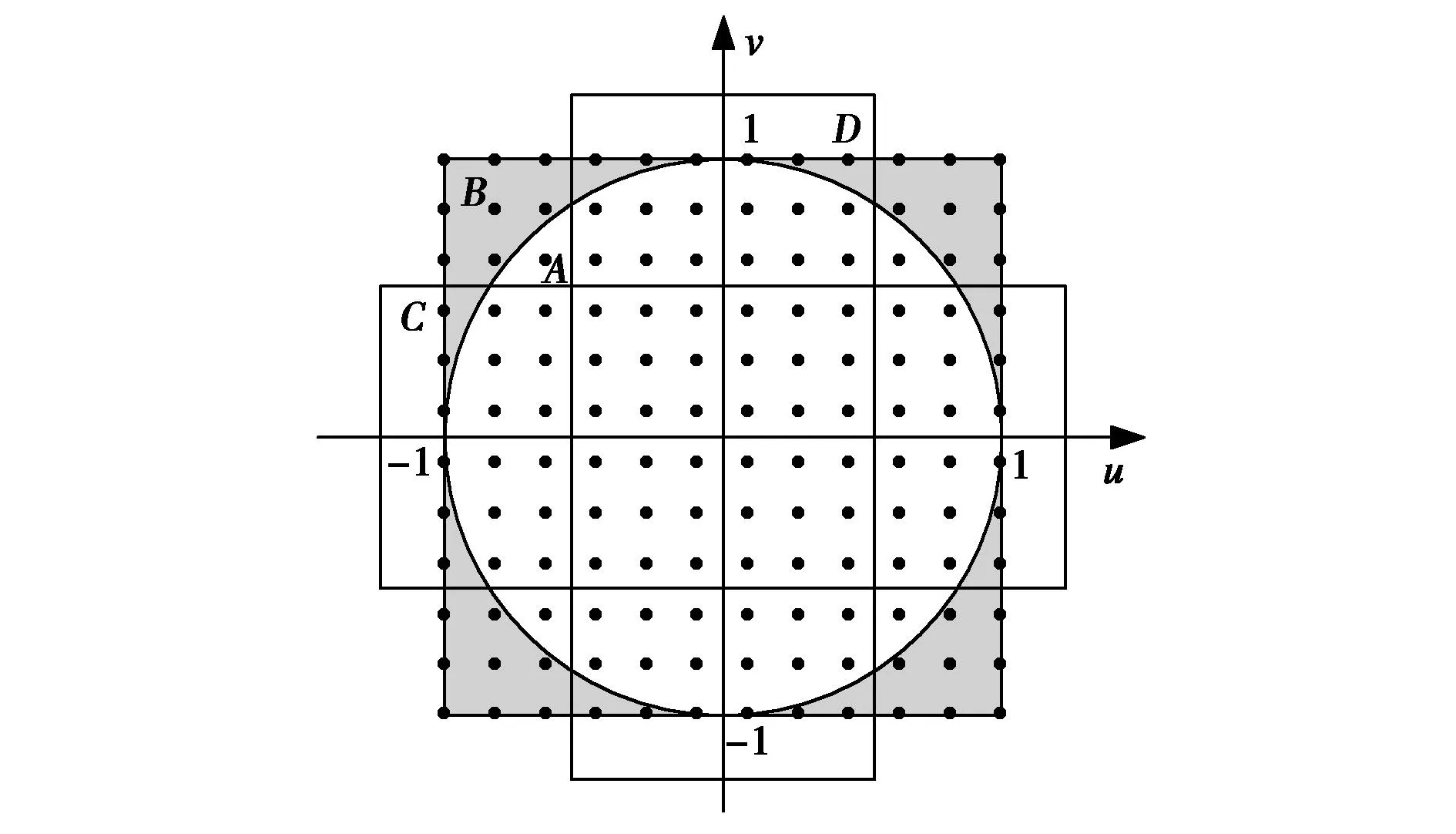
图2 可见空间区域示意图
2.2 逐步截断IFT算法
对于一个给定的稀疏阵,设Mtot表示阵列孔径范围内的阵元总数.T为IFT算法每一次迭代中,处于“开”状态的阵元数目.本文提出的改进IFT算法不依赖于阵列激励阵元的分布,设T=Mtot-i(i=0,1,…,N0),其中,i为迭代次数.N0为最大迭代次数.当i=N0时,T=Tmin,Tmin为处于“开”状态的最少阵元数.随着算法迭代次数的增加,T从Mtot依次减少到Tmin,每迭代一次,处于“开”状态的阵元减少指定的个数,利用IFT算法综合稀疏平面阵的详细步骤如下:
1) 初始化阵元激励A,使阵元激励都取1,虚拟阵元与六边形天线阵列口径外的点Amn取0.
2) 对A施加K×K点二维IFFT得到阵列方向图F,其中K>2*max(M,N).
3) 在F的副瓣区域中,对于副瓣电平高于副瓣电平阈值(Sidelobe Level Threshold, SLLT)的采样点,用SLLT的值替代.
4) 对更新后的F施加K×K点二维FFT,求出新的阵元激励A.
5) 在A的K×K个采样点中,保留和阵列结构匹配的M×N个采样点的值,其余采样点的值被置为0.
6) 根据当前阵列处于“开”状态阵元数量的多少,把具有较大幅度值的T个阵元的激励幅度值设置为1,其余的设置为0.
7) 判断T是否满足条件不大于Tmin,若不满足,T=T-1,重复2)到6)的步骤;若满足,记录迭代过程中最小MSLL值和对应的稀疏阵列结构,试验结束.为了使算法更快的收敛,如果第i次迭代的MSLL比i-1的高3 dB,试验也结束.
3仿真实验结果与分析
为了说明本文所改进的IFT算法的有效性,对一个有1 027个单元(L=18)的六边形平面天线阵进行对称与非对称稀疏优化处理,以改善其最大副瓣电平.在仿真例子中,取d=λ/2,二维IFFT和FFT运算采样点数K×K=512×512,最少激励阵元数Tmin=0.4Mtot.由于SLLT的大小直接决定了优化解的优劣,因此需要选择合适的值进行优化,在本文中,经过反复计算和分析,取SLLT为-31dB.
3.1 六边形天线阵列对称优化处理
由于正六边形有六个对称轴,位于对称轴上的阵元具有6个对称阵元,而位于非对称轴上的阵元则有12个对称阵元.如果在优化过程中,对6个或12个对称阵元进行一次性截断,所得的解很容易陷入局部最优解,且算法会很快满足迭代终止条件而终止.因此只取图1中关于x轴和y轴对称的阵元进行一次性截断.本小节给出了应用改进的IFT算法对六边形阵列对称稀疏优化后的阵元分布图,如图3所示.可以看出,优化得到的六边形稀疏阵列符合阵列优化规律,即在优化阵列中,阵元的稀疏总是发生在阵列边缘,而阵列中心的阵元一般不会被稀疏掉.优化后的阵元数T=487,在所有副瓣区域的MSLL为-27.03dB.与文献[1]中对相同的六边形稀疏平面阵列运用遗传算法进行优化得到的两个主面的MSLL为-26.4dB、阵元数T=517、填充因子f=50.34%,相比MSLL改善了0.6dB、阵元数减少了30个,其阵列成本和MSLL都得到了改善.图4(a)为归一化远场方向三维方向图,可视空间为u2+v2≤1.图4(b)为u=0和v=0截平面的方向图.
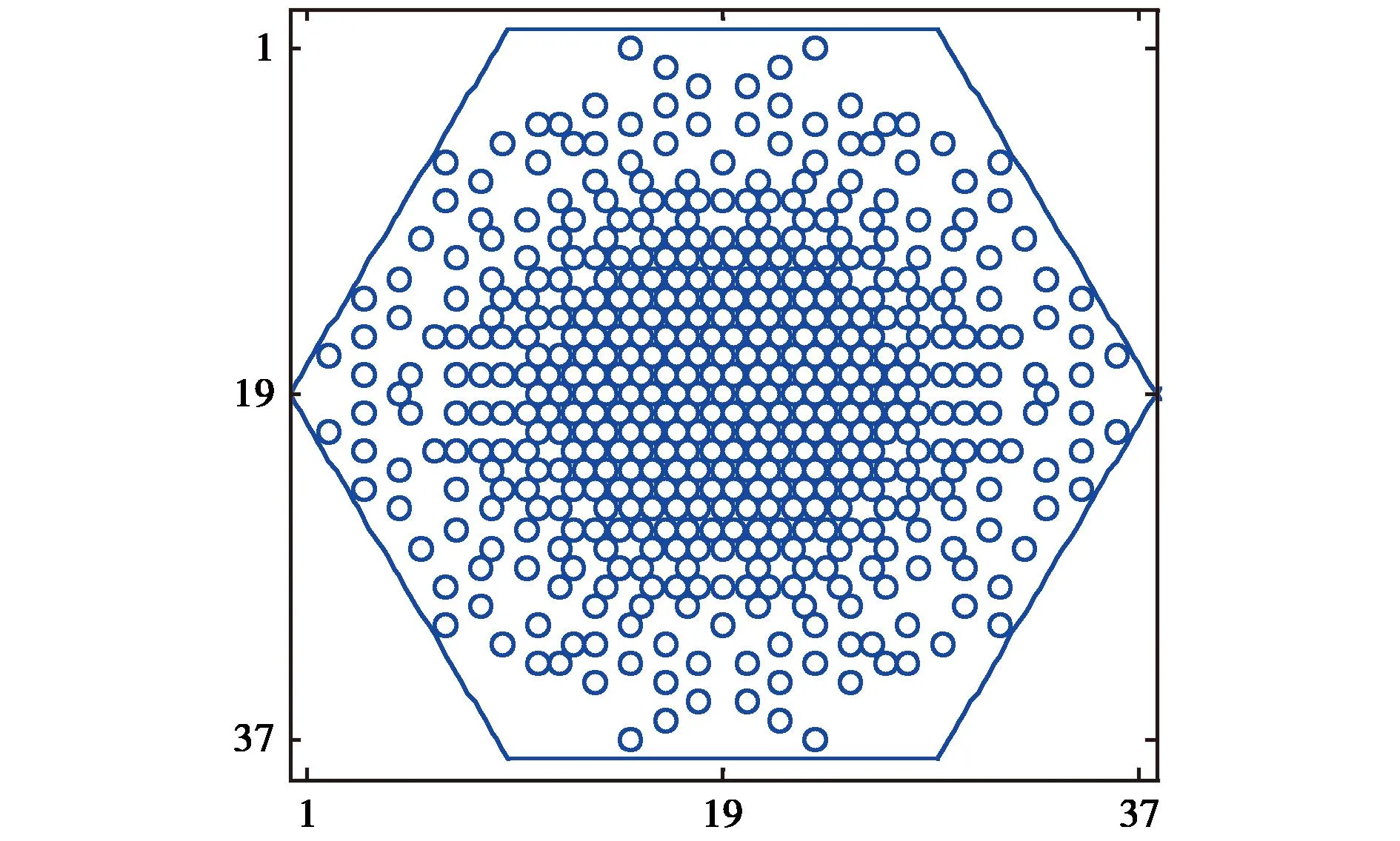
图3 六边形稀疏对称阵列阵元分布图
3.2 六边形天线阵列非对称优化处理
根据阵列的对称特点采用对称优化的处理方式,这样降低了计算量,但同时限制了自由度.本小节应用改进的IFT算法对六边形阵列稀疏非对称优化,优化后阵元分布如图5所示,阵元数T=537,对应的填充因子f=52.29%,在所有副瓣区域的MSLL降低为-28.46dB.同样与文献[1]相比,MSLL进一步改善了2dB,在与对称稀疏优化的相比,副瓣得到了明显的改善.这是由于阵元关于阵列中心非对称分布,增加了可利用的优化自由度,更有利于提高六边形稀疏天线阵列的副瓣性能.图6(a)为归一化远场三维方向图,其可视空间为u2+v2≤1.图6(b)为u=0和v=0截平面的方向图.
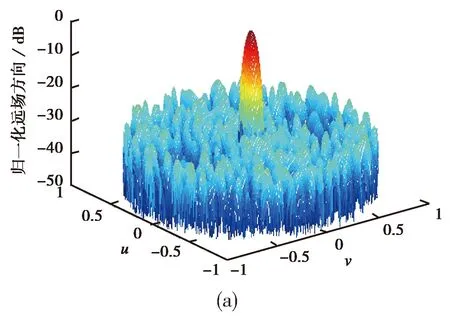
(a) 三维方向图
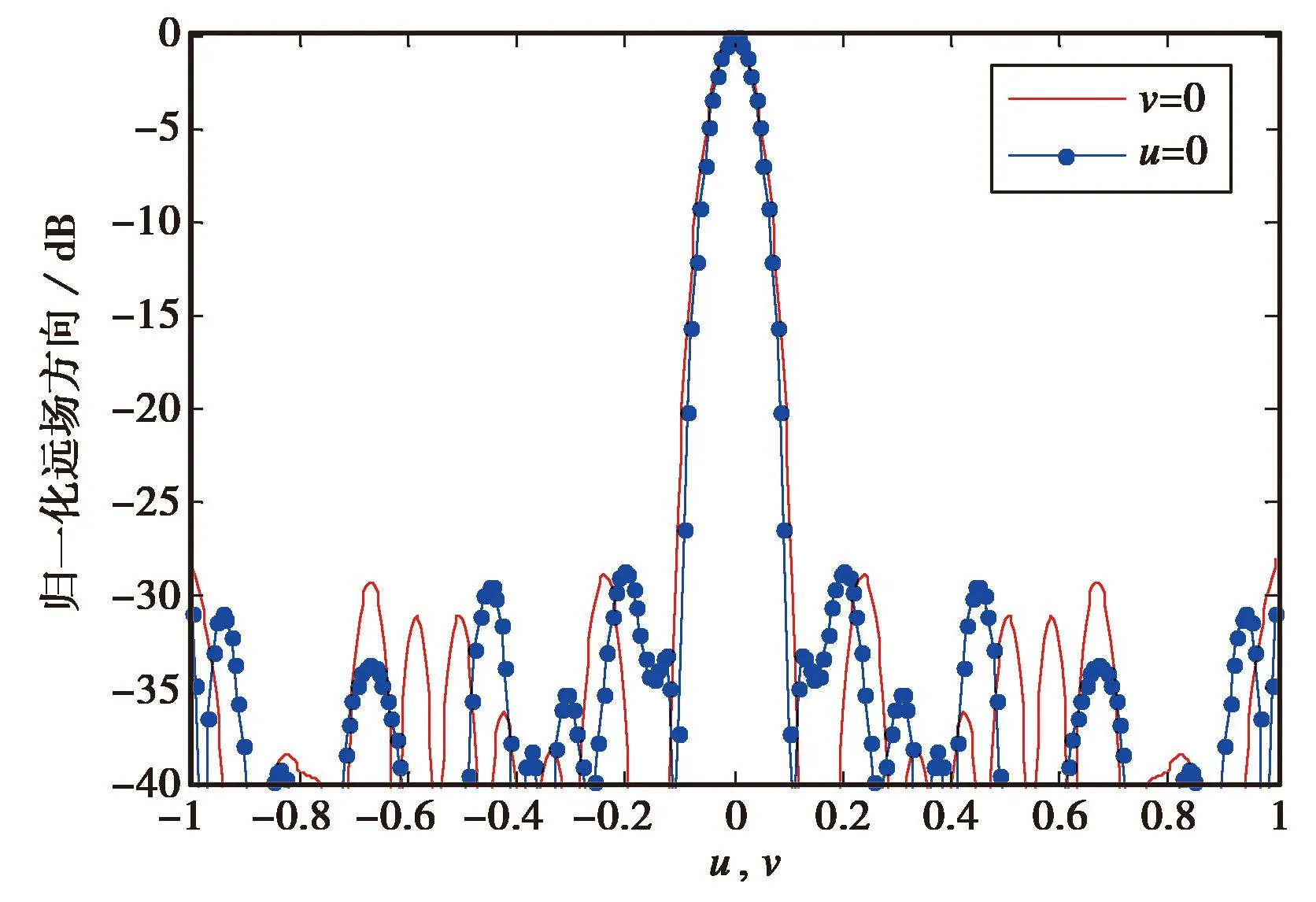
(b) u和v截面方向图图4 对称优化归一化远场方向图
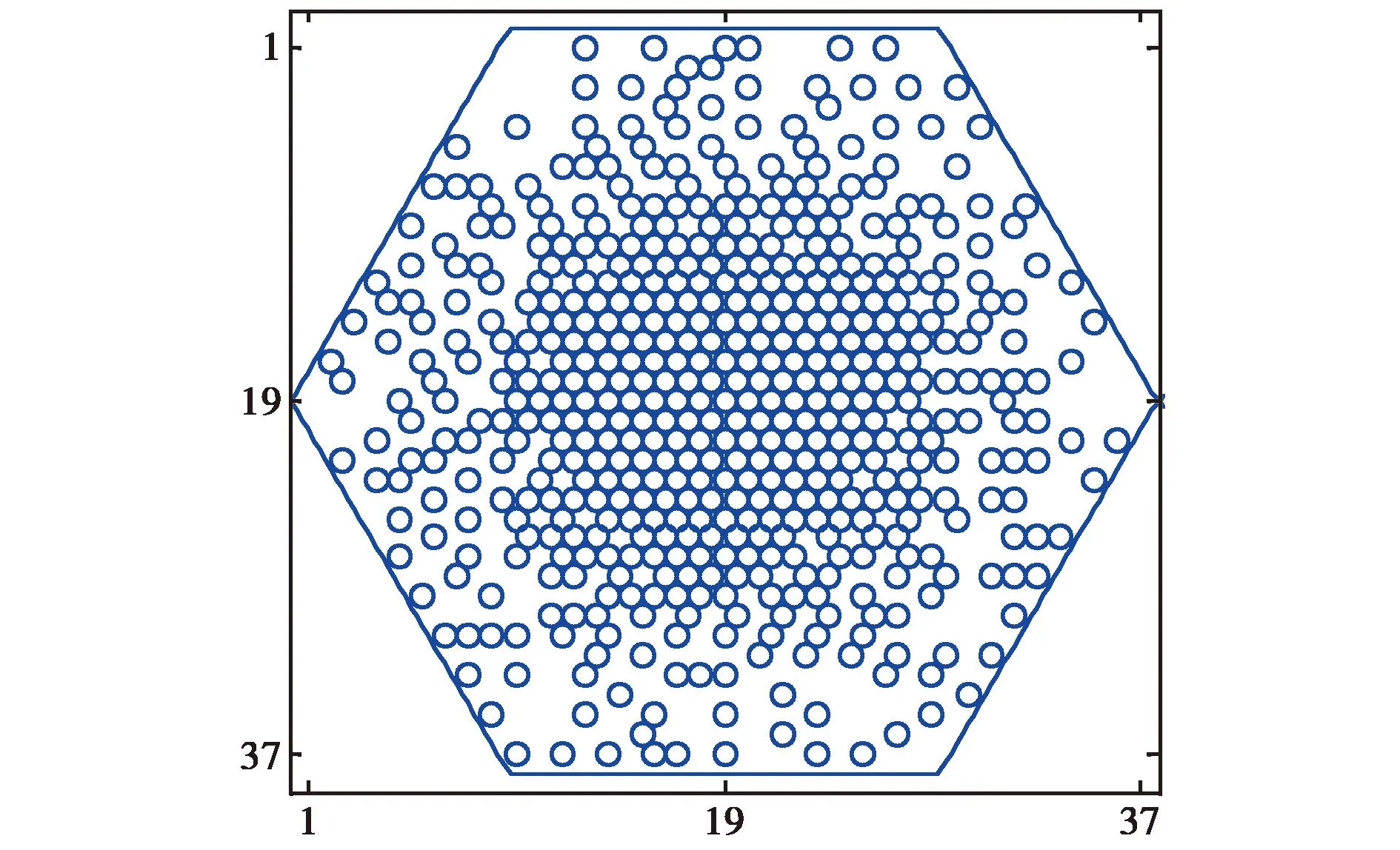
图5 六边形稀疏阵列非对称优化阵元分布图
3.3 算法收敛与速度分析
图7给出了3.2节中运用改进的IFT算法对六边形稀疏阵列非对称优化的MSLL随阵元数减少的变化情况.由图可以看出,在T0=Mtot,即满阵均匀激励的情况下,最大副瓣电平为-16.64dB.随着阵元数的减少,稀疏六边形天线阵列的MSLL也逐步地下降.当T1=537时,阵列的MSLL为-28.46dB达到最小值,较六边形平面满阵天线的MSLL降低了11.8dB.当T=515时,MSLL有另外一个极值-27.53dB.随着阵元数的进一步减少,MSLL不再降低,而在一定范围内波动;当到达T2=430,MSLL迅速升高,优化结果急剧恶化,试验结束.

(a) 三维方向图
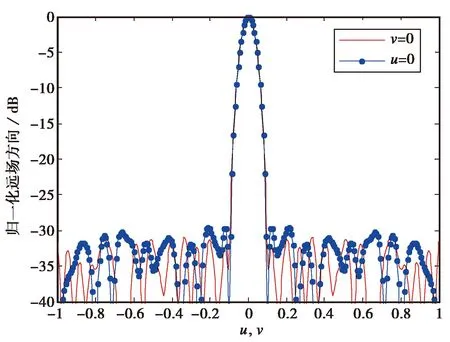
(b) u和v截面的方向图图6 非对称优化远场方向图
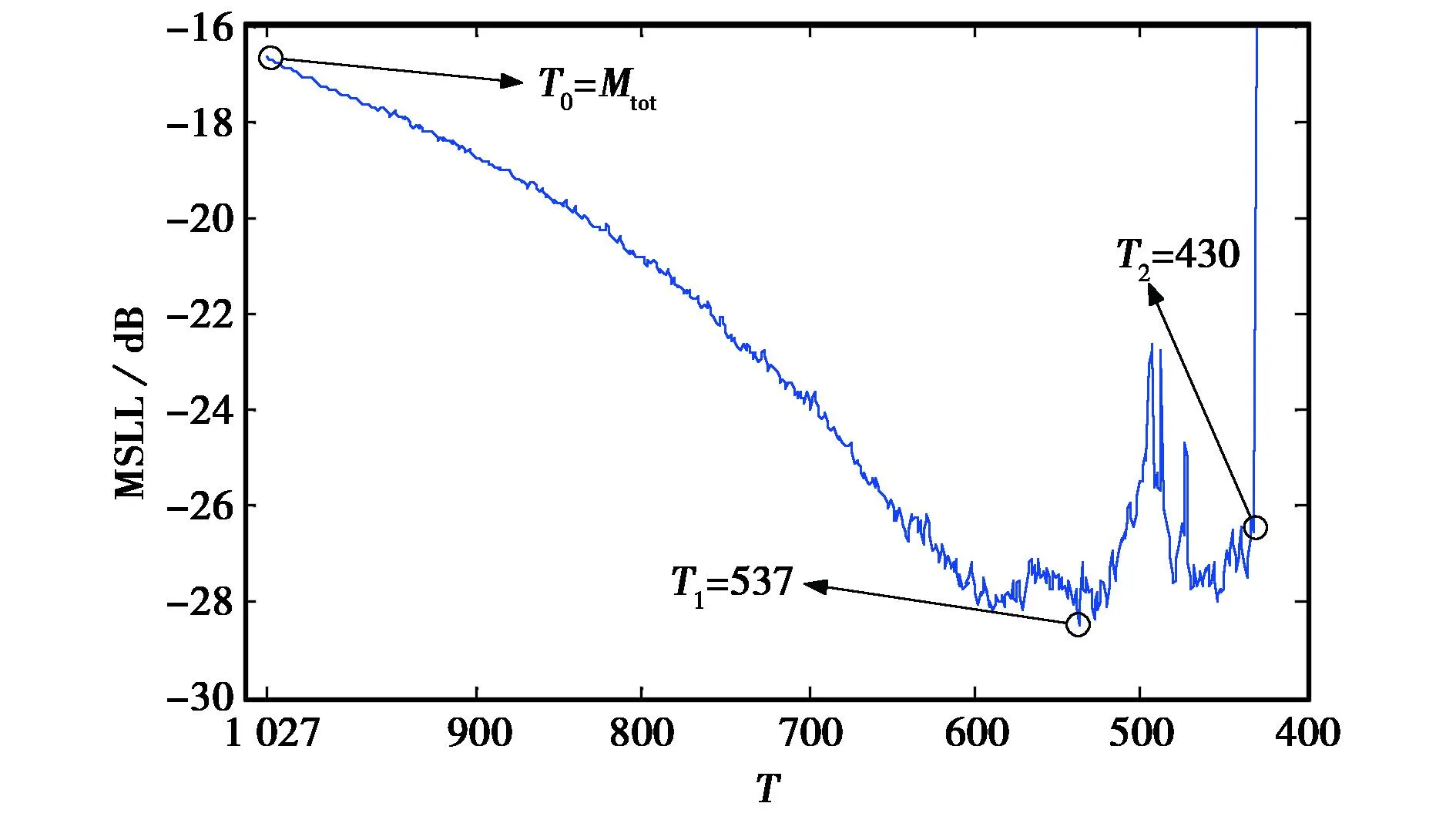
图7 MSLL的收敛情况
对于大型的平面阵列,在采样点很多的情况下,采用阵列叠加原理计算阵因子的传统的智能进化方法需要耗费很长的时间,其次还需要产生等于自由度数量数倍的种群数,在自由度很大的阵列中依次计算每个个体的适应度需要耗费大量的时间,甚至导致计算无法完成.IFT算法通过对阵元激励做IFFT计算阵因子,再通过对调整后的阵因子做FFT来反算阵元激励,因此具有计算速度极快的优点.IFT算法在优化阵列方向图时,表1列出了FFT在计算本文所优化的1 027个阵元组成的六边形阵列方向图所需要的时间:在CPU为Q8300,内存为2G的电脑上.可以看出与阵列叠加原理比较,FFT计算二维方向图综合,具有优化时间短,操作简单等优点.

表1 计算阵列方向图的平均时间 s
4结论
本文提出了一种用于稀疏阵列天线综合的逐步截断IFT算法,该算法不依赖于初始阵元的分布,从满阵迭代逐步剔除数个激励幅度最小的阵元,从而更容易收敛至全局最优解.为了计算六边形天线阵的方向图,通过在口径中添加虚拟阵元的方法,把六边形阵列转化为可以实现二维傅里叶变换的矩形阵列模型.然后利用改进后的IFT算法对六边形阵列天线进行稀疏布阵优化,以改善阵列的最大副瓣电平性能为目的.优化所得到的六边形平面稀疏阵列天线的辐射特性获得了改善,为大型阵列天线的稀疏优化提供了有效途径.该方法使计算量成倍减少,也可用于解决其他种类的矩形阵和三角阵平面阵列天线的稀疏布阵优化,具有很好的工程实用价值.
参考文献
[1]李东风, 龚中麟. 六边形平面天线阵优化稀疏布阵研究[J]. 电子学报, 2002, 30(3): 376-380.
LI Dongfeng, GONG Zhonglin. Research on thinning the Hexagonal planar antenna array[J]. Acta Electronica Sinica, 2002, 30(3): 376-380. (in Chinese)
[2] 王玲玲, 方大纲. 运用遗传算法综合稀疏阵列[J]. 电子学报, 2003, 31(12A): 2135-2138.
WANG Lingling, FANG Dagang. Genetic algorithm for the synthesis of thinned array[J]. Acta Electronica Sinica, 2003, 31(12A): 2135-2138. (in Chinese)
[3] JIN N, RAHMAT-SAMII Y. Advances in particle swarm optimization for antenna design: real-number, binary, single-objective and multiple objective implementations [J]. IEEE Trans on Antennas and Propagation, 2007, 55(3): 556-567.
[4] DONELLI M, MARTINI A, MASSA A. A hybrid approach based o n PSO and Hadamard difference sets for the synthesis of square thinned arrays [J]. IEEE Trans on Antennas and Propagation, 2009, 57(8): 2491-2495.
[5] CHEN Y, YANG S, NIE Z. Synthesis of uniform amplitude thinned linear phased arrays using the differential evolution algorithm[J]. Electromagnetics, 2007, 27(5): 287-297.
[6] ZHANG L, JIAO Y C, WENG Z B, et al. Design of planar thinned arrays using a Boolean differential evolution algorithm[J]. IET Microwaves, Antennas & Propagation, 2010, 4(12): 2172-2178.
[7] KEIZER W P M N. Linear array thinning using iterative FFT techniques [J]. IEEE Transactions on Antennas and Propagation, 2008, 56(8): 2757-2760.
[8] KEIZER W P M N. Large planar array thinning using iterative FFT techniques [J]. IEEE Trans on Antennas and Propagation, 2009, 57(10): 3359-3362.
[9] Keizer W P M N. Synthesis of Thinned planar circular and square Arrays using density tapering[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(4): 1555-1563.
[10]DIETRICH F J, METZEN P, MONTE P. The globalstar cellular satellite system [J]. IEEE trans on Antennas, 1998, 46(6): 935-942.
[11]曾伟一, 梁颖, 黄伟, 等. 非对称直线稀疏阵列的迭代IFT优化方法[J]. 重庆邮电大学学报, 2012, 24(3): 287-291.
ZENG Weiyi, LIANG Ying, HUANG Wei, et al. Asymmetric linear arrays thinning using iterative FFT algorithm [J]. Journal of Chongqing University of Posts and Telecommunications, 2012, 24(3): 287-291. (in Chinese)
[12]王新宽, 焦永昌, 谭艳艳. 自适应迭代傅里叶算法用于阵列方向图综合 [J]. 西安电子科技大学学报, 2013, 40(4): 85-89.
WANG Xinkuan, JIAO Yongchang, TAN Yanyan. Adaptive iteration Fourier technique applied for antenna arrays pattern synthesis [J]. Journal of XiDian University, 2013, 40(4): 85-89. (in Chinese)
刘恒 (1986-),男,湖南人,中国空间技术研究院博士研究生,研究方向:阵列天线设计与优化的研究.
刘波(1963-),男,湖南人,中国空间技术研究院研究员,博士生导师,研究方向:卫星总体设计方面的研究.
谢广钱(1983-),男,江苏人,中国空间技术研究院工程师,博士研究生,研究方向:导航卫星信号多径影响及定量研究.
赵宏伟(1982-),男,山东人,中国空间技术研究院博士研究生,研究方向:空间谱估计、智能优化算法.
Iterative Fourier technique applied for Hexagon thinned array antenna
LIU HengLIU BoXIE GuangqianZHAO Hongwei
(ChinaAcademyofSpaceTechnology,Xi’an710100,China)
AbstractA modified iterative Fourier technique (IFT) is proposed for disadvantage of numerous elements truncated in the thinned planar arrays synthesis of standard IFT. The method initialized form filled arrays and decreased several elements step by step to avoid running into local optimization. Then the modified IFT is applied to design a low side lobe hexagonal planar array by thinning process. Virtual elements are added in the array for translating the array to rectangle for calculating the array factor of hexagon conveniently. The simulated results show that the performance of the hexagonal planar array is better comparing with using genetic algorithm, and also has the advantage of less computation and high speed.
Key wordsarray antenna; thinned array; iterative Fourier technique; sidelobe level
作者简介
收稿日期:2015-01-21
中图分类号TN958.93
文献标志码A
文章编号1005-0388(2015)06-1235-06
