基于小波奇异熵和相关向量机的氢气传感器故障诊断

2015-02-23王冰刁鸣宋凯

电机与控制学报 2015年1期

王冰，刁鸣，宋凯

（1.哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨 150001;2.中国电子科技集团公司第49研究所，黑龙江哈尔滨 150001;3.哈尔滨工业大学电气工程及自动化学院，黑龙江哈尔滨 150001）

王冰1，2，刁鸣1，宋凯3

针对氢气传感器故障问题，提出了一种智能化的传感器故障诊断方法，可以对自身故障状态进行诊断和识别。提出了一种基于小波奇异熵（wavelet singular entropy，WSE）和相关向量机（relevance vector machine，RVM）原理的氢气传感器故障诊断方法，将小波变换和奇异熵两种分析思想相结合，提取信号的完备故障特征;利用小生境粒子群优化算法（niche particle swarm optimization，NPSO）对相关向量机的核参数进行优化，提高故障诊断的准确率。将提出的方法与其他成熟算法进行了比较，实验结果表明所提方法故障诊断识别率达到98%以上，解决了非线性、小样本条件下的传感器故障诊断问题，提高了传感器的可靠性。

小波奇异熵;相关向量机;氢气传感器;小生境粒子群优化;故障诊断

0 引言

氢气作为一种新型能源，在航空、动力等领域得到了广泛的应用，特别是在军事国防领域有着重要的应用价值。但是，氢气也是一种无色无味、易燃易爆、易泄漏的气体，当浓度在4.1%－74.1%vol（volume）时极易发生爆炸［1］，因此对氢气的检测十分必要。例如运载火箭发射过程中需要监测氢气含量;用于向宇宙飞船或核潜艇提供氧气的电解水制氧氢过程中，氢气浓度的监测对保证仓内人员安全起到重要作用［2］。微结构氢气传感器在实现氢气浓度测量的同时，也使故障发生概率增大［3］，因此人们希望了解传感器的工作状态是否正常，测量的数据是否可信。现有的氢气传感器都没有对自身故障状态进行诊断的功能，即认为传感器一直处于正常工作的状态，这样当传感器发生故障时，其输出结果已经偏离了实际情况，可能会造成误报警，降低了检测结果的准确度和可信度，因此对传感器故障状态的诊断就显得非常重要。

目前，常用的故障诊断方法主要有硬件冗余法、解析冗余法、神经网络法和支持向量机（support vector machine，SVM）法等［4］。SVM是其中应用和研究较广泛的一种方法，它通过结构风险最小化原理来提高泛化能力，有效地避免了经典学习方法中过学习和维数灾难等问题，较好地解决了小样本和非线性等实际问题［5］。如Samanta，李凌均等人将其应用于滚动轴承的故障模式分类中［6－7］，Jack L B将其应用于齿轮的故障诊断［8］，沙立成等人将SVM的参数优化后对变压器故障气体进行预测［9］。但是SVM方法也存在一些缺点，其模型的稀疏性有限，支持向量个数基本上随训练样本集的规模成线性增长，可能会造成过适应和预测时间的增加;输出结果是非概率性的，无法确定预测的准确度;模型参数设置复杂，需要给定一个惩罚因子C，这个参数对结果有很大的影响，而且没有固定的确定方法，必须通过大量的交叉验证或附加优化算法来进行确定;核函数受Mercer条件限制等［10］。

相关向量机（relevance vector machine，RVM）是一种新的基于稀疏Bayes学习理论的机器学习方法，由美国学者TIPPING提出［11］。它与SVM具有相同的函数形式和相当的泛化性能，但对核函数的类型没有约束，不需满足Mercer条件的限制，选择范围更广泛，参数设置更简单，只需对核参数进行设置，并且能给出预测的概率信息，比SVM有更强的稀疏性。

本文针对传统故障诊断方法的不足，提出了基于小波奇异熵（wavelet singular entropy，WSE）和RVM原理的传感器故障诊断方法，通过小波分解和奇异熵原理更好地提取信号的非线性特征，将其作为RVM分类器的输入，提高故障诊断的准确率，通过小生境粒子群优化算法（niche particle swarm optimization，NPSO）的参数寻优方法，找到RVM模型的全局最优参数，进而提高了故障诊断模型的性能。

1 小波奇异熵特征提取原理

信息熵（information entropy）是对信号所含信息程度的描述［12］。如果把信号比喻成一个物质系统，其所含的信息越多，信号的随机性和不确定性越大，即信号越紊乱，熵就越大，所以信息熵被看作信号紊乱程度的量度。奇异熵是信息熵的一种，反映了时域信号在奇异谱划分下各模式的不确定程度，也体现了信号能量分布的时域复杂性，即信号能量分布方式越简单，能量越集中于少数几个模式，对应的奇异熵数值就越小;相反，信号越复杂，能量越分散，奇异熵数值就越大。因此，信号奇异熵刻画了信号中奇异成分能量分布的复杂性程度，进而可以用来描述信号的动态特征。

由于小波变换具有良好的时频局部化能力，奇异熵能够描述信号的复杂性特征，因此将两种分析思想相结合可以实现对信号更为完备的特征提取。

设信号x（n）在j（j=1，…，m，m为最大分解尺度）尺度下的小波分解高频分量系数为cDj（k），低频分量系数为cAj（k），进行单支重构后得到对应的高频信号分量Dj（n）和低频信号分量Aj（n）。由多分辨分析原理，原始信号x（n）可分解为

式中，Dj（n）表示信号x（n）在不同频段下的分量。将m个尺度的分解结果Dj（n）构成一个（m+1）×n的矩阵D（m+1）×n，根据信号的奇异分解理论，D可分解为式（3）的形式为

式中，对角阵Λ的主对角线元素λj（j=1，2，…，l）便是小波变换结果矩阵D（m+1）×n的奇异值。为了定量描述信号的频率成分及分布特性，定义小波奇异熵为［13］

式中:Δpi为第j阶增量小波奇异熵;k为λj中非零元素个数。

小波空间的奇异熵在综合冗余信息的基础上，直接反映了被分析信号时－频空间中特征模式能量的分布奇异性，特别适合包含信息量较多的强噪声信号的特征提取，可以获得更好的非线性特征提取和噪声抑制能力，进而提高故障诊断的准确率。

基于小波分解和奇异熵的信号特征提取步骤如下:

1）小波分解及确定基小波、分解层数和小波系数;

2）求取小波重构信号矩阵，对各层分解系数进行重构后，得到信号各频段下的分量Dj（n）（j=1，…，m+1），由此确定小波重构信号矩阵D（m+1）×n;

3）根据奇异值分解理论和式（3），计算小波重构信号矩阵的奇异值谱λj（j=1，2，…，l），将λj代入到式（5）得到小波奇异熵;

4）将得到的小波奇异熵与步骤1）中确定的小波分解系数一起组成特征向量，实现氢气传感器故障信号的特征提取。

2 RVM分类原理

式中，εn服从均值为0，方差为σ2的高斯分布，σ2假设为未知量，通过数据训练迭代更新获取，一般可根据训练集目标值的噪声方差赋予初值。监督学习模型的一般表达式为

式中:K（x，xi）为核函数;ωi为权重向量。由于εn满足高斯分布，对于各自独立的目标值tn，可得整个数据集的似然函数为

式中:t=（t1…tN）T;ω=（ω0…ωN）T;Φ=［φ（x1），φ（x2），…，φ（xN）］T为N×（N+1）的矩阵;φ（xn）=［1，K（xn，x1），K（xn，x2），…，K（xn，xN）］T，为了避免直接采用极大似然方法估计ω和σ2的过适应，根据贝叶斯理论，定义高斯先验概率分布

式中，超参数向量α由N+1个超参数组成，根据以上定义和贝叶斯公式，给定训练集的后验概率可以表示为

其中，μi是式（11）中均值向量μ的第i个元素，MacKay方法中定义γi=1－αiNii，其中Nii为式（11）中方差∑的对角线上的第i个元素。

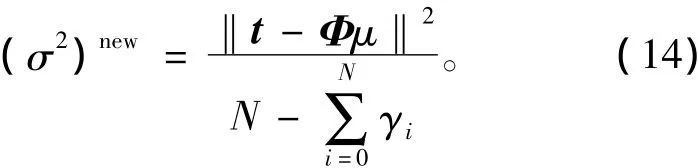
式中，tcn∈{0，1}为分类目标值，这里不考虑方差影响。通过Laplace逼近方法可近似得到统计方差和权值向量为

3 实验分析

本文采用上述方法，研究了氢气传感器的故障诊断模型，如图1所示，并验证了算法的有效性。

图1 故障诊断模型原理图Fig.1The model schematic diagram of fault diagnosis

3.1 故障状态分析

根据半导体氢气传感器结构特点及气敏特性分析，由于氢气传感器大多长时间使用，且使用环境较恶劣，因此其敏感膜容易受到污染而失效，导致传感器出现失效、过载等故障;敏感单元的加热电极和敏感膜的脱落也可能出现此故障。由于气体传感器的内阻较高，很容易受到外界的干扰，但是一般干扰时间都很短，因此会导致冲击故障。由于敏感单元内部放大电路工作异常、内部调理电路出现故障或是电源损坏、测量电路的电极损坏、焊点开裂等原因，会产生敏感单元出现过载、变化率异常和掉电故障。本文选用了河南汉威电子的MQ－8系列半导体氢气传感器作为测试传感器，由于在使用过程中不可能短时间内出现故障状态分析中的各种故障类型，因此本文在故障状态分析和实测数据的基础上，仿真得到了几种常见的典型故障。选取氢气浓度点为1 000 PPM时的测量数据作为原始数据，图2分别仿真了氢气传感器发生失效、过载、变化率异常、冲击和掉电故障时的输出数据。从图2（a）可以看出，60 s发生失效故障后传感器输出的电压值接近恒定;图2（b）为传感器发生过载故障的输出数据，60 s后输出异常变大，超出其测量范围;图2（c）为传感器发生变化率异常故障时的输出数据，60 s后输出发生不规则变化;图2（d）显示，在58 s到63 s间数据产生了一个较大的尖峰，说明此时发生了冲击故障;图2（e）中，60 s后传感器输出为0，发生了掉电故障。

图2 传感器典型故障数据Fig.2The typical fault data of sensor

3.2 基于小波奇异熵的故障特征提取

采用本文的小波奇异熵故障特征提取的方法，选取与上节相同氢气浓度点为1 000 PPM时的测量数据作为原始数据对算法进行验证。将5种故障状态和正常状态共6种状态的数据进行标准化处理，然后对标准化的数据进行小波分解，由于故障信号的波形在一系列的突变点之间是平滑的，所以要求小波函数中存在许多阶消失矩，db4小波函数在时域上是有限支撑的，具有4阶消失矩，因此选择db4小波作为小波基函数，并对其进行三层小波分解。图3为6种状态下小波分解后的近似系数。对每个节点的小波系数进行重构，确定小波重构信号矩阵，计算小波奇异熵。本文以基于距离判据的特征评估准则作为小波系数的选取原则，计算各特征（小波系数）的评估因子，从分解得到的近似系数中选取特征评估因子较大的5个系数作为特征量，将其与小波奇异熵一起组成特征向量。

图3 传感器各种状态下小波分解近似系数Fig.3Wavelet decomposition approximated coefficients in various states of sensor

在实验的情况下得到了6种状态下的各30组数据，数据长度为120，将小波分解的5个系数与其对应的小波奇异熵一起组成特征向量。表1给出了6种状态下传感器输出信号的各一个特征向量。

表1 传感器各种状态下的特征向量Table 1The feature vectors in various states of sensor

3.3 基于NPSO参数优化的RVM故障诊断

由于RVM算法核参数的选择会直接影响分类模型的准确度，而采用遍历搜寻方法进行参数选择具有一定的盲目性，且需要花费大量的时间，最后找到的参数也未必是全局最优解。针对RVM核参数选择难的问题，本文提出了基于小生境粒子群优化算法的RVM参数寻优方法。由于惯性权重PSO算法收敛到一定精度时无法继续优化，利用基于共享机制的NPSO算法来对核函数的参数进行优化，将小生境共享机制引入到粒子群算法中，增加了粒子种群的多样性，避免一般粒子群算法的早熟现象，提高收敛速度，能够快速找到全局最优参数。

本文采用k遍历交叉验证（k－fold cross validation，k－CV）的原则设置RVM参数的适应度函数，以此来评价RVM的分类性能。根据k－fold基本原理，将训练集随机的近似等分为k组（一般为均分，k≥2），对每个子集数据分别做一次验证集，同时其余的k－1组子集数据作为训练集，这样会得到k个RVM模型，用这k个模型验证集的分类错误率的平均值作为此参数的适应度函数，有

式中:yf（i）表示第i个验证集中的错误分类数量; yc（i）表示第i个验证集中的正确分类数量。

本文选取RVM模型中最常用的高斯核函数，也就是通常所说的RBF核函数，因为对于此核函数，只要选择合适的核参数，训练样本几乎总能在特征空间中被线性分开。实验随机选取6种状态下的数据各10组对所建立的相关向量分类机进行训练，对余下的6种状态各20组数据作为测试样本进行故障模式识别。根据样本数量，选取k=3，其中NPSO算法种群规模为20，最大迭代次数100次，小生境距离常数L为1.5，惩罚因子Pen为1 000。优化过程的适应度变化如图4所示，可以看出在第53代以后，最佳适应度值近似收敛于全局最优解，对应的RVM分类模型最优参数为σ2=0.513 6。

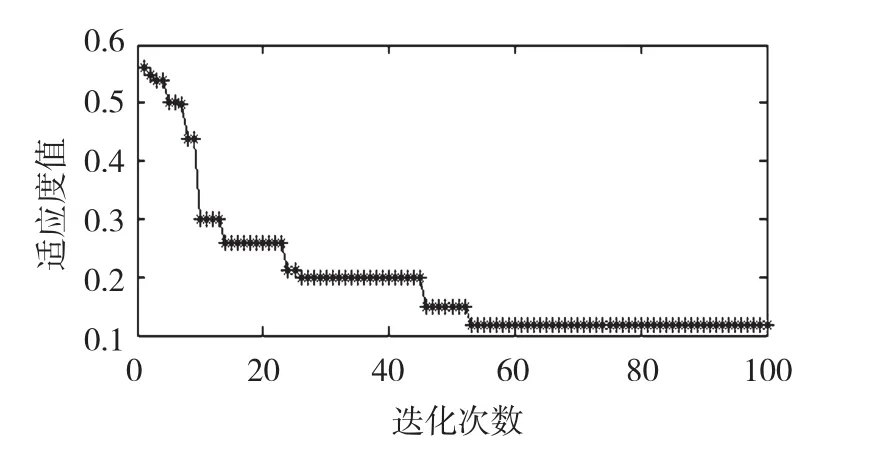
图4 适应度值迭代曲线Fig.4Fitness value iteration curve

利用上面获得的最优参数，应用相关向量机分类原理对传感器故障类型进行诊断，并取相同的测试样本和训练样本，与RBF神经网络、SVM方法进行了比较，如表2所示。其中，RBF网络的输入节点数为6，隐层节点数采用自动确定的方法，输出节点数为3;SVM算法中选取与RVM算法相同的RBF核函数，误差惩罚因子C=100，核宽度σ=4。从表2中可以看出，在小样本数据的情况下，本文所用的方法可以准确地区分出传感器的6种状态，验证了该方法的有效性，也验证了本文所用的方法在小样本情况下仍然具有良好的预测和推广能力。

表2 各种分类方法性能比较Table 2The comparison of classification performance in various methods

4 结论

本文研究了一种基于相关向量机方法的氢气传感器故障诊断方法，是氢气传感器智能化发展趋势的体现，解决了现有氢气传感器不能诊断自身故障状态的问题，提高了传感器可靠性。重点研究了基于小波奇异熵的故障特征提取方法和基于小生境粒子群的RVM参数优化算法，提高了相关向量机的分类速度和准确率，对其他类型传感器的故障诊断研究也有借鉴作用。

［1］WINTER C.Hydrogen energy－abundant，efficient，clean:a debate over the energy system of change［J］.International Journal of Hydrogen Energy，2009，34:1－52.

［2］CLARK W W，RIFKIN J，O＇CONNOR T，et al.Hydrogen energy stations:along the roadside to the hydrogen economy［J］.Utilities Policy，2005，13（2）:41－50.

［3］ELAOUD S，HADJ－TAIEB L，HADJ－TAIEB E.Leak detection of hydrogen natural gas mixtures in pipes using the characteristics method of specified time intervals［J］.Journal of Loss Prevention in the Process Industries，2010，23（3）:637－645.

［4］毕晓君，柳长源，卢迪.基于PSO－RVM算法的发动机故障诊断［J］.哈尔滨工程大学学报，2014，35（2）:245－249.

BI Xiaojun，LIU Changyuan，LU Di.Engine fault diagnosis method based on PSO－RVM algorithm［J］.Journal of Harbin Engineering University，2014，35（2）:245－249.

［5］TIPPING Me.Sparse bayes learning and the relevance vector machine［J］.Machine Learning Research，2001:211－244.

［6］李凌均，张周锁，何正嘉.基于支持向量数据描述的机械故障诊断研究［J］.西安交通大学学报，2003，37（9）:910－913.

LI Lingjun，ZHANG Zhousuo，HE Zhengjia.Research of mechanical system fault diagnosis based on support vector data description［J］.Journal of Xian Jiaotong University，2003，37（9）: 910－913.

［7］SAMANTA B.Gear fault detection using artificial neural networks and support vector machines with genetic algorithms［J］.Mechanical System and Signal Processing，2004，18（3）:625－644.

［8］JACK L B，NANDIA K.Fault detection using support vector machines and artificial neural networks，augmented by genetic algorithms［J］.Mechanical System Sand Signal Processing，2002，16 （2）:373－390.

［9］沙立成，宋珺琤.基于改进粒子群优化LS—SVM的变压器故障气体预测［J］.华北电力大学学报，2011，38（1）:35－38.

SHA Licheng，SONG Juncheng.Predicting method for dissolved gas in transformer oil based on modified particle swarm optimization［J］.Joumal of North China Electric Power University，2011，38（1）:35－38.

［10］沈默，廖瑛，尹大伟.RVM在航空发动机故障诊断中的应用研究［J］.计算机工程与应用，2012，48（25）:220－223.

SHEN Mo，LIAO Ying，YIN Dawei.Application of relevance vector machines to aero－engine fault diagnosis［J］.Computer Engineering and Applications，2012，48（25）:220－223.

［11］段青，赵建国，马艳.优化组合核函数相关向量机电力负荷预测模型［J］.电机与控制学报，2010，13（6）:33－38.

DUAN Qing，ZHAO Jianguo，MA Yan.Relevance vector machine based on particle swarm optimization of compounding kernels in electricity load forecasting［J］.Electric Machines and Control，2010，13（6）:33－38.

［12］HUANG X J，CHOI Y K，YUN K S，et al.Oscillating behaviour of hazardous gas on tin oxide gas sensor Fourier and wavelet transform analysis［J］.Sensors and Actuators B，2006，115（7）:357－364.

［13］DING H，GE H，LIU J.High performance of gas identification by wavelet transform－based fast feature extraction from temperature modulated semiconductor gas sensors［J］.Sensors and Actuators B，2005，4（107）:749－755.

（编辑:刘琳琳）

Fault diagnosis of hydrogen sensor based on wavelet singular entropy and relevance vector machine

WANG Bing1，2，DIAO Ming1，SONG Kai3
（1.College of Information and Communication Engineering，Harbin Engineering University，Harbin 150001，China; 2.Chinese Electron Science and Technology Conglomerate 49th Research Institute，Harbin 150001，China; 3.School of Electrical Engineering and Automation，Harbin Institute of Technology，Harbin 150001，China）

Aiming at the fault problem of hydrogen sensor，an intelligent fault diagnosis method which can diagnose and distinguish the fault state of the sensor was proposed.The fault diagnosis method based on wavelet singular entropy and relevance vector machine was researched，the feature of fault signal was extracted completely by combining the theory of the wavelet transform and singular entropy.The niche particle swarm optimization algorithm was used to optimize kernel parameter of RVM，and the accuracy of the fault diagnosis was improved.The proposed method was compared with other mature algorithms.Results indicates that the fault diagnosis recognizable rate reaches 98%.It resolves the problem of sensor fault diagnosis under the condition of nonlinear and small sample，and promote the reliability of sensor.

wavelet singular entropy;relevance vector machine;hydrogen sensor;niche particle swarm optimization;fault diagnosis

10.15938/j.emc.2015.01.014

TP 206.3

1007－449X（2015）01－0096－06

2014－05－11

国家自然科学基金（61201306）

王冰（1984—），女，博士研究生，研究方向为传感器信号检测、处理;

刁鸣（1960—），男，博士，教授，研究方向为宽带信号处理、检测与识别;

宋凯（1982—），男，博士，讲师，研究方向为传感器及检测技术。

王冰