考虑噪声因子的永磁同步电机转矩脉动分布特性分析
2015-02-23武志勇郭宏钱浩
武志勇,郭宏,钱浩
(北京航空航天大学自动化科学与电气工程学院,北京 100191)
考虑噪声因子的永磁同步电机转矩脉动分布特性分析
武志勇,郭宏,钱浩
(北京航空航天大学自动化科学与电气工程学院,北京 100191)
针对永磁同步电机在批量生产过程中,受到电机尺寸加工偏差及材料属性偏差等噪声因子的影响,存在批量生产电机的转矩脉动峰值会产生分散性的问题。为了研究存在噪声因子条件下转矩脉动峰值的分布特性,通过采用敏感性分析的方法得到了影响转矩脉动峰值的主要噪声因子包括磁钢形位公差和材料属性偏差,槽口尺寸偏差及气隙尺寸偏差。通过理论分析和解析计算得到了存在噪声因子的情况下,批量生产的电机产品转矩脉动峰值的统计分布规律。得出在电机可行设计域内,不同电机设计方案,其批量产品转矩脉动峰值的均值和标准差呈正比关系,并通过粒子群优化结果证明了结论的有效性。
永磁;同步电机;敏感性分析;统计分析;转矩
0 引言
永磁同步电动机具有反电势正弦度好、控制性能优良、等诸多优点,广泛应用于高精度电机伺服系统内。限制永磁同步电机整体性能提升的关键问题在于电机的转矩脉动[1-4]。转矩脉动作为高精密伺服系统的寄生特性,一直受到人们的重视。国内外学者对转矩脉动开展了深入的机理分析并研究从电机设计层面对转矩脉动峰值进行有效的抑制。
但是,在实际生产过程中,产生了如下两个问题,其一,由于加工过程存在不可抑制的结构尺寸公差和材料属性偏差等噪声因子,而转矩波动又对这些噪声因子异常敏感,进而造成了实际加工之后,电机转矩脉动值偏离了设计期望值。其二,由于在批量生产的电机中,每台电机的噪声因子情况均不一致,从而造成了在批量生产电机内部,转矩脉动峰值呈现一定的分散性。这就使得初始的电机设计期望值无法正确的反映出批量电机内部转矩脉动的特性。进而影响了伺服系统的控制性能。
为了研究转矩脉动峰值在批量生产电机内部的分布规律,一些文献针对此问题开展了分析。文献[5-6]重点分析了磁钢加工偏差条件下,齿槽转矩峰值在批量电机内部的分布情况,文献[7]对由磁钢偏差引起的反电势有效值的分散性进行统计分析。文献[8]针对转矩脉动在存在加工偏差的条件下,进行电机结构尺寸优化,提升电机系统的稳健性。
从上述文献可以总结出,首先,由于电机性能的分散性由加工公差引起,因此在分析批量电机关键特性的分散性时,文献均针对影响性能分散性最甚的偏差进行处理。比如磁钢偏差等。其次,这些文献均采用了统计的手段对分散性进行描述。这种统计学规律往往可以由样本的均值和标准差来表示。均值反映了批次电机整体性能与设计目标值所接近的程度,标准差反映的为批次电机的性能分散性。通过这两个统计学变量,能够较为直观的反映出批量电机特性的整体分布规律。
在解决转矩脉动分布问题中,均值和标准差之间的关系值得进一步深入研究,其反映了批量电机关键特性的分布情况,对两个变量关系的研究也是对电机性能分布的研究。通过对均值和标准差的统计分析,可以得到在一定的公差条件下,批量电机在制造过程中所呈现的分布规律。目前,文献已对齿槽定位转矩和反电势波形进行了有效的分析,还没有针对转矩脉动分散性的有效统计分析。本文通过理论分析和解析计算讨论了各种加工偏差对均值和标准差的影响程度,研究了在可行域内考虑加工偏差等噪声因子后电机转矩脉动特性的均值和标准差之间的关系。
本文首先针对电机制造过程中产生的电机尺寸和形位公差进行敏感性分析,得到对于电机关键特性较为敏感的噪声因子。之后针对几种典型的电机制造公差,对批次电机在可行域内均值和标准差的分布规律进行理论推导和解析计算,得到了均值和标准差之间的数值关系。最后采用粒子群算法分别将均值和标准差作为优化目标进行优化,通过优化结果证明了结论的有效性。
1 噪声因子敏感性分析
对于噪声因子的敏感性分析是转矩脉动统计分析的前提。在电机加工过程中,噪声因子主要包括以下几种:
1)定子和转子部分:槽开口误差(Δbo),气隙偏差(Δa-g),转子偏心(ΔInn)。
2)磁钢部分:磁钢厚度(Δw),磁钢贴偏(Δδ),剩磁偏差(Δbr),充磁角度偏差(Δθ)。
噪声因子示意图如图1所示。

图1 电机各种偏差示意图Fig.1The tolerances of the motors
敏感性分析主要通过计算含噪声因子情况下与理想无噪声因子条件下转矩脉动峰值的比值,得到转矩脉动对于各噪声因子的敏感程度。
本文选择两种较为典型的分数槽集中绕组永磁同步电机作为敏感性分析的对象,分别是14极18槽电机以及22极24槽电机。这两种分数槽集中绕组永磁同步电机的反电势正弦度好,能够抑制由于反电势非正弦造成的转矩脉动,同时两种电机的槽数和磁钢数的公倍数较大也相对削弱了电机的齿槽转矩。由于这两种极槽配合的电机转矩脉动值较小,噪声因子会导致实际生产值严重偏离设计期望值,造成了设计和生产结果之间的很大的误差。因此采用这种低转矩脉动的永磁同步电机极槽配合结构进行敏感性分析是十分必要的。
电机的初始设计方案已经完成。具体电动机参数见表1。

表1 电机初始化设计方案Table 1Motor initial design parameter
由于电机转矩脉动可分为电磁转矩脉动(Tem)以及齿槽转矩(Tcogg)两部分,因此对转矩脉动这两个部分分别进行敏感性分析。
在敏感性分析中噪声因子不同尺度的公差带也会对敏感性产生影响,为了避免由于公差带选择过大或过小干扰敏感性分析的结果,14极18槽电机的部分噪声因子选择2~3个公差带,综合分析在不同公差标准的情况下,噪声因子的敏感程度,所有公差带的选取参考国标GB/T 1800.3要求。敏感性分析采用有限元方法进行。在有限元计算时,针对每种电机模型均进行3次网格剖分,并检查计算结果误差在1%范围之内,从而避免了由于有限元时空离散对计算结果所造成的影响。有限元结果如表2,3所示,表中的百分比是指含噪声因子时与理想无噪声因子时相比,转矩脉动峰值相对增加的百分比。
根据敏感性分析结果可以得出:Tem和Tcogg对于Δδ,ΔBr,Δθ三个噪声因子异常敏感,噪声因子的微小偏差会造成转矩脉动特别是齿槽转矩的强烈变化。同时Δbo以及Δa_g对于齿槽转矩也较为敏感,因此根据以上结论,在统计分析时针对如下几个噪声因子进行:Δδ,ΔBr,Δθ,Δbo以及Δa-g。以上分析是依据设计资料和计算结果得到。

表2 电机定子和转子部分尺寸偏差的敏感性分析Table 2Sensitive analysis of the size errors of the stators and rotors

表3 电机磁钢部分尺寸偏差的敏感性分析Table 3Sensitive analysis of the size errors of the magnets
2 批量生产电机转矩脉动峰值均值和标准差分析
本节分析电机在各种噪声因子作用下,批量生产电机转矩脉动峰值的统计规律以及均值和标准差之间的关系。根据敏感性分析的结果,转矩脉动峰值对磁钢类噪声因子最为敏感,因此主要对磁钢类噪声因子造成的影响进行分析。首先通过理论推导对批量电机转矩脉动均值和标准差之间的关系进行说明,随后采用解析计算方法对批量生产电机转矩脉动的统计分布进行解析计算。本节计算所使用的电机案例为上节所述的14极18槽电机。
2.1 磁钢类噪声因子
主要针对Δδ,ΔBr,Δθ这三种磁钢类噪声因子展开研究。
根据文献[5-6]可知,电机的转矩脉动可分为固有的转矩脉动(TNHC)和附加转矩脉动(TAHC)。其中,TNHC为电机不存在噪声因子时转矩脉动的固有部分。而TAHC为考虑噪声因子作用后,附加的转矩脉动部分。磁钢偏差如图2所示;

图214 p18s电机磁钢偏差示意图,每块磁钢包含磁钢贴偏,剩磁偏差,以及充磁角度偏差.Fig.2Tolerances of the 14 poles and 18 slots motors,including the magnet misplacements,Br errors and magnetization directions errors
当磁钢的偏差远小于磁钢名义尺寸时,计算由磁钢偏差所产生的TAHC可进行两种近似处理。
1)由各噪声因子作用产生的TAHC与噪声因子数值之间呈线性关系;
2)各块磁钢产生的TAHC之间满足相移关系;
文献[5,7]针对以上两个近似处理有详细的理论证明。当不考虑磁路饱和时,上面的结论严格成立,当考虑磁路饱和时,结论近似成立。
根据以上的近似,首先得到一块磁钢单位偏差产生的TAHC的波形,通过相移和比例缩放及线性加权可得到各块磁钢噪声因子总作用下的TAHC波形。
在电机加工制造过程中,上述三种磁钢类噪声因子在实际工程加工中常按标准正态分布处理[5,7]。其分布规律如下所示:

其中,σerr为三种磁钢误差的标准差。将σerr数值作为单位偏差数值。根据单位偏差数值对噪声因子进行归一化处理。
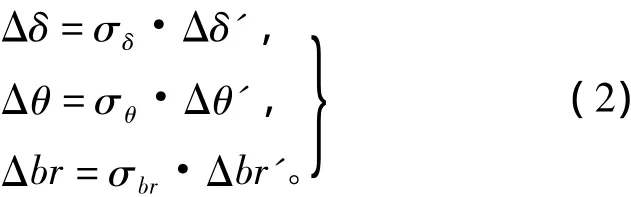
其中,σδ,σθ,σbr分别为三种公差的标准差。因此,Δδ',Δθ',Δbr'∈[~,N(0,1)]。
由于三种噪声因子的推导过程一致,因此在计算时由Δerr'统一代表Δδ',Δθ',Δbr'不再单独列写表达式。
通过以上的分析,当各磁钢存在噪声因子时,噪声因子产生的TAHC可由傅里叶级数展开式表示为:

在分析过程中,各个频次的幅值是考虑的核心问题。其表达式可以写为:

当h≠nNm,n=1,2,3…时为一闭合矢量和;其向量大约有一半的长度在实轴上,一半在虚轴上。因此
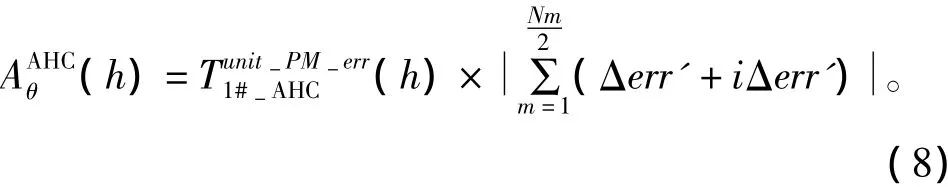
由于上式的实部和虚部两部分为标准差相同的正态分布,因此向量的模值服从瑞利分布。瑞利分布的期望为,标准差为
因此,当h≠nNm,n=1,2,3…
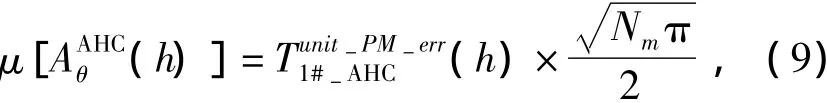
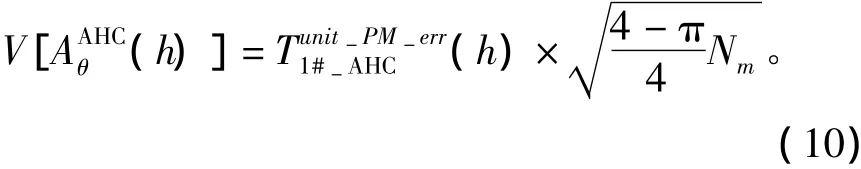
可以看到,磁钢误差导致的转矩脉动分散性,其期望和标准差都与电机本身的电磁环境(h)相关,并且还与磁钢的块数以及磁钢偏差的分布相关。根据上述推导可知:

从式11中可以看到,附加转矩脉动峰值在大部分频次的期望和标准差均成正比,而在一些频次上均值和标准差的规律则有变动。转矩脉动峰值是对各频次的峰值进行矢量求和的结果。因此转矩脉动的峰值会由一些含有较大转矩脉动均值和标准差的频次所主导。虽然期望和标准差的比值会有所改变,但其整体上应仍呈现正比关系。
上述是针对一种噪声因子独立作用时的分析结论,当三种噪声因子共同作用时,由于三种偏差的幅值远小于磁钢尺寸和材料属性名义值,其各自作用产生的TAHC可看做相互独立的随机变量,当加权三种噪声因子的计算结果后,不改变均值和标准差之间的比例关系。
因此可得出当电机存在磁钢类噪声因子时,其转矩脉动的分布规律服从均值和标准差呈正比的正态分布。
为了进一步验证得到的结论,通过仿真模拟实际批量生产的电机转矩脉动的分布情况对上述理论推导进行验证。为了符合实际工况的需要,对电机的可行设计域进行限定,其可行设计域的上下限如表4所示。在电机可行设计域内对电机的各尺寸进行随机组合,选取50个电机设计方案作为实验对象,每个实验对象在磁钢公差带范围内随机生成1 000台电机样本,其中的每块磁钢三种噪声因子均严格服从正态分布。
尽管有限元计算能够有效的得到精确的转矩脉动波形,但采用有限元方法对此问题进行计算时会消耗大量的计算时间。因此,本文采用建立解析模型方法代替有限元方法用以计算转矩脉动特性。文献[9-10]提出的Exact Subdomain方法在电机磁路弱饱和时能够精确的得出电机的电磁分布规律,本文针对Exact Subdomain方法对其进行改良,使其能够有效的计算加工偏差对转矩脉动的影响。虽然Exact Subdomain方法是基于电机开路的电磁解析计算方法,在处理带载问题时会受到磁路饱和的影响产生一定的计算误差,但针对统计学的计算,由于噪声因子对电机磁路饱和程度的影响非常小,在含有不同噪声因子的各电机内,由饱和所造成的计算偏差程度基本一致,因此饱和对于均值和方差的影响可近似视为相同且对均值和方差的整体关系不构成颠覆性的影响。因此采用Exact Subdomain方法能够有效的反映两者之间的数值关系。在计算时重点考虑了磁钢贴偏,磁钢的剩磁误差以及充磁方向偏差情况下的磁场分布。
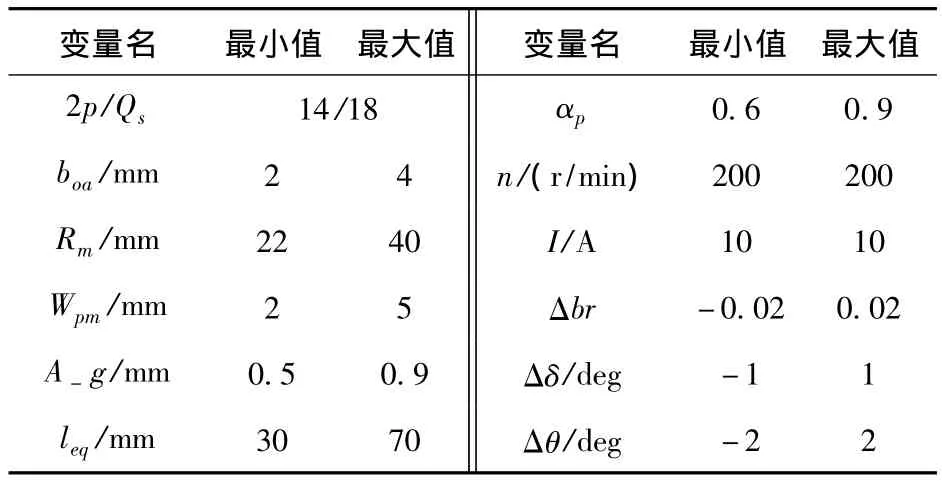
表4 电机设计变量可行域范围及噪声因子范围Table 4Range of the parameters and the noise factors
采用解析方法对50个电机设计方案的1 000台含噪声因子的样本进行转矩脉动计算,分别得到各实验对象转矩脉动峰值均值和标准差值。
通过解析计算,50个电机设计方案转矩脉动峰值的均值和标准差分布规律如下图所示:根据图3所示,各电机设计方案的均值和标准差基本呈现正比关系。

图3 50个电机设计方案转矩脉动均值和标准差Fig.3Expected values and the standard deviation of the torque ripple peak values in 50 motors
2.2 定子噪声因子
关于定子类噪声因子,主要针对Δbo和Δa_g展开研究,如图4所示。根据敏感性分析的结论,两种噪声因子对转矩脉动峰值的影响要远小于磁钢类噪声因子的影响。因此这里不做理论推导,而是通过解析计算的方法得到存在两种偏差情况下转矩脉动的分布特性。

图4 14p18s电机槽口偏差以及气隙偏差示意图Fig.4Slots and air gap errors of the 14p18s
在电机设计可行域之内,选择50个电机设计方案,每个实验对象在定子偏差公差带范围内随机生成1 000台样本,得到50个电机设计方案均值和标准差的分布图如图6、图7所示。图5为槽口偏差时的分布图,图6为气隙误差的分布图。从图中可以看到槽口偏差所引起的性能分散性,转矩脉动峰值的均值和标准差没有任何联系,是呈散乱分布的。而气隙偏差近似呈现正比关系,但与磁钢相比分布较散乱。

图5 50个电机设计方案存在槽开口偏差时转矩脉动均值和标准差Fig.5Expected values and standard deviations of the torque ripple in 50 motors

图6 50个电机设计方案存在气隙偏差时转矩脉动均值和标准差Fig.6Expected values and standard deviations of the torque ripple in 50 motors
2.3 同时存在定子和磁钢噪音因子
当电机同时存在磁钢和定子噪声因子时,同样在可行设计域内随机组合50个电机设计方案,电机的各种噪声因子均在所给定的公差带内变动,服从正态分布规律。每个电机设计方案进行1 000台样本的转矩脉动计算,得到50个电机设计方案转矩脉动的均值和标准差。其分布可由图7所示。

图7 50个电机设计方案在定子和磁钢主要噪音因子存在的条件下转矩脉动的均值和标准差。选择1#,2#,3#电机进一步的样本统计分布规律分析Fig.7Expected value and standard deviations of the torque ripple values in 50 motors designs with main noise factors.Choosing 1#,2#,3#motor to accomplish the statistical analysis
从图7中可以看到,50个电机设计方案的转矩脉动均值和标准差依然呈现线性分布。这是由于磁钢偏差对电机性能分散性所造成的影响比槽口和气隙偏差要大的多,因此,磁钢偏差的影响主导了性能分散性的分布。在图7中选择三个不同的电机设计方案。图8显示了三台电机在可行设计域范围内的转矩脉动分布特性,当转矩脉动均值变大时,其分散性也变大,如2#电机;当转矩脉动均值变小,分散性也变小,转矩脉动分布,如1#电机。

图8 1#,2#,3#电机样本中1 000台样机的转矩脉动的分布情况Fig.8Torque ripple peak values distributions of 1 000 1#,2#and 3#motors
综上所述,可以得到如下结论,永磁同步电机在设计可行设计域内,各种加工偏差影响下,批次电机的均值和标准差是成正比的。其分布规律服从均值和标准差呈正比的正态分布。
3 粒子群算法优化验证
采用多目标优化的方式验证批量电机转矩脉动的均值标准差之间的正比关系。
针对批量生产电机的分散性进行优化。在优化过程中,将电机的输出平均转矩(Tav)的倒数作为一个目标,将1 000台的电机样本转矩脉动的均值(Me1000)或标准差(std1000)作为另一个目标,分别开展两目标优化。优化目标分别为

如果两个优化过程所得到的最优解和最劣解是一致的,则证明了使用均值或者使用标准差作为电机优化的目标,两者是等效的,两个目标之间可进行相互替代,从而验证了两个目标的线性关系。
优化采用粒子群(PSO)优化算法,其优化变量为[boa,Rm,Wpm,A-p,leq,αp];电机的可行设计域如表4所示。
采用含精英归档策略的PSO算法进行优化。优化中粒子群个数为50,精英集合为40个,进化代数为20。C1=C2=0.8,其流程如图9所示。

图9 PSO优化算法流程图Fig.9Flow chart for the PSO optimization
图10显示了两个优化过程的最终结果。
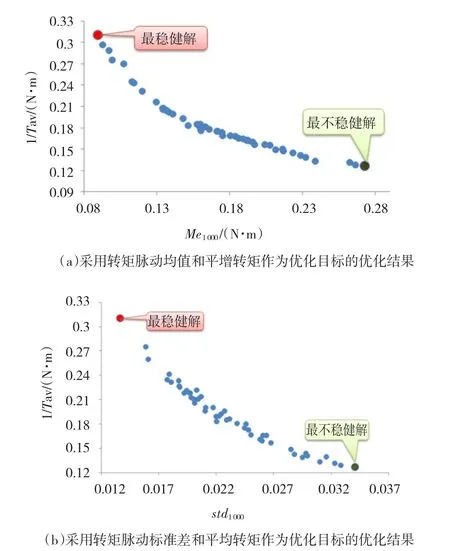
图10 两个不同优化目标的优化结果Fig.10Optimization results for two different objectives
表5显示了两个优化结果得到的最稳健解和最不稳健解。从表中可以看到,最稳健解完全一致,最不稳健解仅在槽口变量上有0.3 mm的差异。从两个优化过程得到的优化结果中可以看到,采用均值或标准差进行的两目标优化,优化结果是一致的,因此两个目标在优化过程中是可以等效替换的,从统计角度分析,均值和标准差是成正比关系的。

表5 两目标优化结果Table 5The results of the two different optimization
从表5中可以看到通过进行永磁同步电机的稳健设计,电机产品的稳健性显著提高,从而使得电机产品转矩脉动峰值的均值和标准差均有大幅的下降,这就保证了电机产品兼备低转矩脉动及低性能分散性。
4 结论
1)通过噪声因子敏感性分析得到对转矩脉动较为敏感的噪声因子为磁钢的尺寸和材料属性偏差,以及气隙和槽口的尺寸偏差。
2)当存在电机加工制造偏差时,批量生产电机转矩脉动峰值的均值和标准差近似呈正比关系,其分布规律服从均值和标准差呈正比的正态分布。
3)通过进行稳健设计,提高了电机产品的稳健性,抑制了产品整体的转矩脉动峰值及产品的性能分散性。
[1]齐蓉,林辉,陈明.无刷直流电机换向转矩脉动分析与抑制[J].电机与控制学报,2006,10(3):287-290.
QI Rong,LIN Hui,CHEN Ming.Analysis and attenuation on commutation torque ripples of brushless DC motor[J].Electric Machines and Control,2006,10(3):287-290.
[2]王淑红,熊光煜.无刷直流电机换相转矩脉动减小及动态仿真[J].电机与控制学报,2008,12(2):169-173.
WANG Shuhong,XIONG Guangyu.Commutation torque ripple minimization and dynamic simulation of brushless DC motor[J].Electric Machines and Control,2008,12(2):169-173.
[3]李耀华,刘卫国.永磁同步电机直接转矩控制不合理转矩脉动[J].电机与控制学报,2007,11(2):148-152.
LI Yaohua,LIU Weiguo.Unreasonable torque ripple of direct torque control in permanent magnet synchronous motor[J].Electric Machines and Control,2007,11(2):148-152.
[4]郭宏,钱浩.永磁同步电机低转矩脉动的稳健设计[J].中国电机工程学报,2012,32(24):88-95.
GUO Hong,QIAN Hao.Robust design for reducing torque ripple in permanent magnet synchronous motor[J].Proceedings of the CSEE,2012,32(24):88-95.
[5]HEINS G,BROWN T,THIELE M.Statistical analysis of the effect of magnet placement on cogging torque in fractional pitch permanent magnet motors[J].IEEE Transactions on Magnetics,2011,47(8):2142-2148.
[6]GASPARIN L,CERNIGOJ A,MARKIC S,et al.Additional cogging torque components in permanent-magnet motors due to manufacturing imperfections[J].IEEE Transactions on Magnetics,2009,45(3):1210-1213.
[7]SIMON-SEMPERE V,BURGOS-PAYAN M,CERQUIDESBUENO J R.Influence of manufacturing tolerances on the electromotive force in permanent-magnet motors[J].IEEE Transactions on Magnetics,2013,49(11):5522-5532.
[8]PONOMAREV P,PETROV I,PYRHONEN J.Influence of travelling current linkage harmonics on inductance variation,torque ripple and sensorless capability of tooth-coil permanent-magnet synchronous machines[J].IEEE Transactions on Magnetics,2014,50(1):1-8.
[9]ZHU Z Q,WU L J,XIA Z P.An accurate subdomain model for magnetic field computation in slotted surface-mounted permanentmagnet machines[J].IEEE Transactions on Magnetics,2010,46 (4):1100-1115.
[10]WU L J,ZHU Z Q,STATON D A,et al.Comparison of analytical models of cogging torque in surface-mounted pm machines[J].IEEE Transactions on Industrial Electronics,2012,59(6): 2414-2425.
(编辑:张诗阁)
Distribution characteristics analysis of torque ripple in permanent magnet synchronous motors considering the noise factors
WU Zhi-yong,GUO Hong,QIAN Hao
(School of Automation Science and Electrical Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
In mass productions of permanent magnet synchronous motors(PMSM),the torque ripple dispersion is caused by the sizes errors and the material properties variations,which can also be named as noise factors.In order to analyze the distribution of torque ripple in mass productions of PMSM,the sensitive analysis was operated and the most sensitive noise factors which greatly affect the torque ripple were obtained that are the magnets misplacement properties error,the slot opening error and the air-gap size error.Then the distribution of the torque ripple in mass productions was estimated by the firstly the theoretical analysis and by the analytical calculation.The relationship of the mean value and standard derivation of the torque ripple in mass production are linear which is then proved by the optimum design results.
permanent magnets;synchronous motors;sensitivity analysis;statistical analysis;torque
10.15938/j.emc.2015.01.002
TM 34
A
1007-449X(2015)01-0008-08
2014-01-25
国家自然科学基金(51277007)
武志勇(1985—),男,博士,研究方向为特种电机设计及驱动控制器设计;
郭宏(1969—),男,博士,教授,博士生导师,研究方向为特种电机及其控制;电机多物理场综合设计与优化等;
钱浩(1985—),男,博士,研究方向为高精度伺服电机设计与驱动控制。
武志勇
