基于干扰观测器的飞行仿真转台完全跟踪控制
2015-06-26陈松林单梅林王丽斌
陈松林,单梅林,王丽斌
基于干扰观测器的飞行仿真转台完全跟踪控制
陈松林,单梅林,王丽斌
(哈尔滨工业大学控制与仿真中心,黑龙江哈尔滨150001)
针对飞行仿真转台不断提升的性能要求及其多速率采样的工作特点,提出了一种新的鲁棒完全跟踪控制策略。针对完全跟踪前馈控制依赖于系统精确数学模型的问题,通过引入干扰观测器来消除模型摄动和外部扰动,使得被控对象的特性在给定的频段内始终趋近于标称模型,充分保证了PTC的作用。仿真结果表明即使结合简单的PID闭环控制器,系统的跟踪性能也获得了很大的提升。给出PTC和DOB的具体设计方法,并对方法的有效性进行了对比仿真验证。结果表明,与已有方法相比,所提控制方法对模型摄动和力矩扰动的抑制能力更强,跟踪性能更好。
飞行仿真转台;完全跟踪控制;干扰观测器;PID;扰动抑制
0 引言
现代战争对武器的性能要求越来越高,作为制导武器地面仿真的关键试验设备之一,飞行仿真转台也同样需要具备更高的动态性能。如何通过控制方法的改进来提高转台的跟踪精度一直是一个亟待解决的问题。
前馈控制是拓展系统频带,提高跟踪精度最有效的方法之一。理论上,将被控对象的逆模型作为前馈控制器可以实现系统的完全跟踪控制,但是离散被控对象模型中常存在不稳定的零点,因此得到的前馈控制器是不稳定的。研究人员针对这种非最小相位系统提出了两种前馈控制方案[1]:一是稳定零极点相消法(stablepolezerocancelingcontroller,SPZC),这种控制器将稳定的零极点抵消,但由不稳定零点带来的幅值以及相位误差都不能够消除;二是美国加州大学伯克利分校M.Tomizuka教授提出的零相差前馈控制器(zerophaseerrortrackingcontroller,ZPETC),通过近似零点的方法来构造前馈控制器,它可以利用超前指令使得系统的相差在整个频域范围内为零并且在频率较低的情况下,幅值误差也基本为零。但是随着频率的增加,增益发生变化,幅值误差扩大,限制了频带的扩展。这些尝试虽然对前馈控制器做了一定的改进,但由于依旧是基于传统的前馈控制器结构,所以即使在没有模型摄动以及外界扰动的理想情况下也不能实现完全跟踪。
日本学者H.Fujimoto提出并完善了一种利用多速率采样系统指令周期与控制周期不同的特点,利用超前指令实现完全跟踪控制(perfecttracking controller,PTC)[2]的一整套方法,H.Fujimoto等人在文献[3-6]中对该方法的具体应用进行举例说明。PTC前馈控制器的思想就是利用多速率采样系统的特点,将单输入单输出的被控对象描述成多输入多输出的状态方程,从而建立控制变量与被控对象状态的关系,实现由期望状态与期望被控输入的转换。近年来,完全跟踪控制方法受到了广泛关注,取得了一些有益的研究结果[7-10]。考虑到实际应用中,飞行仿真转台的控制周期可以根据指令更新周期设定,而且速度指令可用,满足PTC的应用条件。吴云洁等人首次将PTC控制方法与HI控制器相结合并应用于飞行仿真转台,但是HI控制器只能提高闭环系统的鲁棒性,却不能有效抑制模型参数摄动和外部扰动对PTC性能的影响。这使得PTC的作用不能充分发挥。
受以上研究结果启发,本文也研究了PTC控制方法在飞行仿真转台中的应用问题。与文献[10]不同的是,本文针对PTC对精确数学模型的依赖,通过引入干扰观测器来抑制模型摄动和外部扰动,使得被控对象在给定频段内始终趋近于标称模型,保证了PTC能够充分发挥作用。进而通过位置环PID控制器设计来保证闭环系统问题,并进一步提高系统动态跟踪精度,最后的仿真比较充分说明这种方法的优越性。
1 PTC前馈控制器设计
在应用PTC之前,首先介绍一下PTC设计思想。由于PTC只适用于多速率采样系统,而且其控制周期必须小于指令周期并且是其整数倍。具体关系如图1所示。

图1 指令周期与控制周期关系图Fig.1Theintervalrelationbetweenreference signalandinput
图中,Tu为系统的控制周期,Tr为指令周期,且Tr=nTu,这里n为系统的阶数。符号i与k的区别在于i表示iTr时刻,k表示kTu时刻,比如系统在iTr以及kTu时刻的状态可以分别表示为X[i]= X[iTr],X[k]=X[kTu]
下面首先给出PTC前馈控制器的设计方法。假定被控对象以Tu为离散周期,以双线性法为离散化方式,得到的离散状态空间表达式为

式中,X[k]为kTu时刻系统状态,u[k]为kTu时刻系统控制输入,y[k]为kTu时刻系统输出,As,bs和cs分别为离散化后的系统矩阵,输入矩阵和输出矩阵。
由式(1)可以得到

结合式(2)与图1可得到
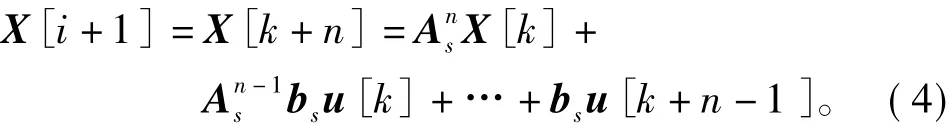
若令

那么综合式(3)、式(4)和式(5),可以得到以Tr为采样周期的被控对象的状态空间表达式为

其中,

由式(6)可以得到

其中,C1即为所求前馈控制器,从式(5)可以看出U[i]包含了各个控制周期的控制输入。而式(7)说明此前馈控制器分母为1,所以不存在不稳定零点的问题。结合式(6)与式(7),可以得到如下的结论:当系统输入为下一时刻的期望状态时,输出为当前时刻的期望输入,即在iTr时刻,可以实现完全跟踪。当然,要实现完全跟踪的前提是,必须要有期望的状态作为PTC的输入。并不是所有系统都能满足这一要求,但对于飞行仿真转台而言,其输入的位置指令是通过仿真机通过速度信号积分得到的,因此仿真机可以同时提供位置指令及相应的速度甚至加速度信号,而这些信号恰好就是PTC所需要的期望状态。
值得注意的是前面的推导都是基于标称模型进行的,然而飞行仿真转台这类实际系统总会存在建模偏差、参数摄动以及各种外部扰动,这些因素必然会破坏PTC的性能,因此有必要设计鲁棒控制器来抑制或消除上述不确定性的影响,以充分发挥PTC的作用。
2 干扰观测器设计
为消除模型参数摄动和外部扰动的对PTC的不利影响,一个有效的方法就是利用干扰观测器估计出干扰和摄动的大小,然后对其进行补偿来消除或抑制其影响。为此设计图2所示的干扰观测器。
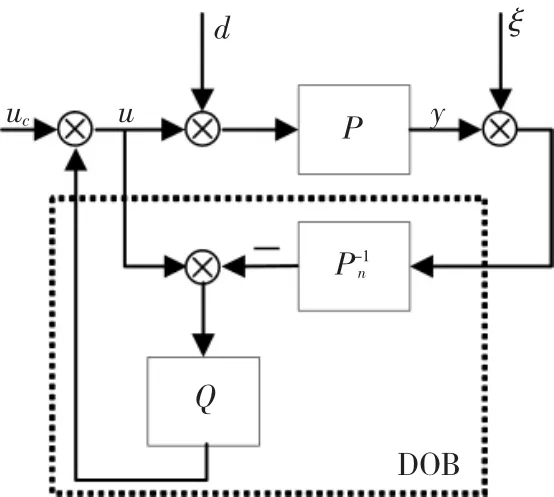
图2 干扰观测器的原理框图Fig.2Diagramofdisturbanceobserver
图中,uc为控制器输出,d为噪声干扰,P为被控对象(包含模型摄动以及外部干扰),Pn为被控对象的标称模型,Q为低通滤波器。
干扰观测器的设计思想为:利用被控对象标称模型的逆模型来预估控制输入u,并与实际的控制输入做差得到系统扰动,并将其反馈达到消除扰动的目的。然而,系统的逆模型一般是不可物理实现的,所以需要引入低通滤波器Q,另一方面Q也有抑制噪声的作用。因此鲁棒控制器的设计也就简化为低通滤波器Q的设计。控制信号u到输出y、干扰信号d到输出y以及噪声信号ξ到系统输出y的传递函数分别为
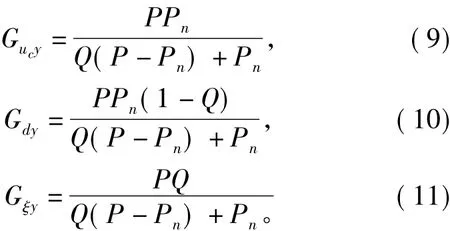
针对上述传递函数可对Q设计提出如下的限制条件:
1)相对度;为了能使系统可以物理实现,Q的分母与分子阶数之差应当大于Pn的分母与分子阶数之差。
2)低频幅值限制;为使Gucy尽可能的接近Pn,Q在工作频段即低频段其幅值应当约为1。
3)高频幅值限制;为使Gξy尽可能的小,Q在高频段其幅值应为0。
4)鲁棒稳定性[11];假定被控对象模型乘性摄动为P=Pn(1+Δ),则Q鲁棒稳定性的充分条件为‖Δ(s)Q(s)‖∞≤1
为进一步确定低通滤波器的结构,下面根据飞行仿真转台被控对象模型进行分析。飞行仿真转台每个自由度都可以用如下模型描述[10]。

其中J为折算到电机轴的负载转动惯量,B为等效阻尼。
在此模型的基础上加入适当扰动,可得原理结构图如图3所示。

图3 被控对象原理结构图Fig.3Structureofthecontrolledplant
其中:dT为等效力矩扰动;ξn为量化噪声;k为控制量到输出力矩等效增益。
结合低通滤波器的限定条件可知:对于上述二阶系统,Q阶数之差应大于等于2;为满足条件Q在工作频段近似为1,其分子分母都应含有常数项1。针对上述要求,参考文献[12]采用如下结构形式的低通滤波器
以上光盘6盘起邮,20元/盘;购买数量达到11盘以上(含11盘)15元/盘;购买数量达到21盘以上(含21盘)10元/盘。购买时请注明光盘代号。本社读者服务部长期办理以上光盘的邮购业务,汇款请写清详细收货地址、电话及所购光盘名称和数量。联系(汇款)地址:长沙市八一路59号《农家致富顾问》杂志社,收款人姓名:读者服务部;邮编:410001;联系电话:0731-84462961;联系人:刘卫民。
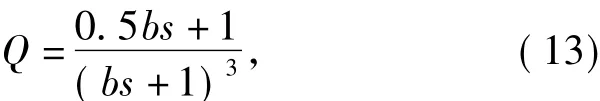
其中b>0。它的取值大小与系统的鲁棒性存在如下关系:b越小,Q的幅值接近1的频段越宽,对模型摄动以及力矩扰动的抑制能力越强,同时会对高频噪声更加敏感,反之亦然[13]。在对b进行选取时,除了考虑低频性能及高频噪声的限定条件外,还要考虑鲁棒Q的鲁棒稳定性约束。为保证这一要求,只要在已知被控对象的不确定性界Δ的情况下(可以根据系统参数摄动范围确定、也可通过测试得到),绘制1/Δ和备选Q的幅频特性曲线,如果Q整个频段内都处于1/Δ下方,即可满足鲁棒性条件[14]。由此可以确定满足鲁棒性稳定性约束的参数b的取值范围。
在PTC前馈控制器与干扰观测器设计完成后,最后利用PID控制器进行来实现闭环控制,保证系统的稳定性,并且进一步提升系统的性能。由于干扰观测器的引入,可以忽略不确定性的影响,仅针对标称模型来设计PID控制器。设计时,先利用劳斯判据得到控制系统的稳定条件,再按照一般PID整定方法来确定控制器参数。
至此,整个控制系统框图可以由图4所描述,其中CPTC为PTC前馈控制器,Pn为系统标称模型,P为系统实际模型。

图4 整个控制策略的原理框图Fig.4Principlediagramoftheproposed controlstrategy
3 系统仿真
为便于比较,选取文献[10]中的模型参数,进行仿真验证。被控对象标称模型(12)中各参数取值为:Jn=0.001053为等效转动惯量,Bn=0.106316为等效阻尼。指令周期取Tr=2ms,控制周期取Tu=1ms。那么可得到式(6)所描述的参数矩阵为

结合式(7)与式(14),可以求得PTC前馈控制器为

利用文中提到参数b的选取方法确定b=0.001。则干扰观测器的传递函数为
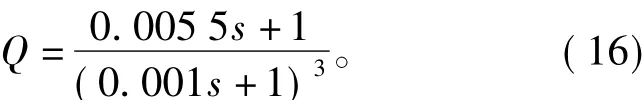
令被控对象中的P中J=1.1Jn,B=1.2Bn,图5给出了标称模型(实线)与补偿后的实际对象(虚线)的Bode图。可见在低频段两条曲线几乎重合,这充分说明了干扰观测器对参数摄动的补偿能力。
设PID控制器为K(s)=kp+ki/s+kds,结合系统标称模型,可以求得系统的闭环传递函数为

根据劳斯判据得到如下稳定条件。

根据上述稳定性条件并按照PID调试的一般规则,最终确定PID参数为ki=2,kd=0,kp=45。
在Matlab环境下进行仿真,参考文献[10]引入模型摄动、参考文献[15]在Simulink模型中加入摩擦干扰和量化噪声。然后设定幅值为0.5°,频率分别为1Hz、4Hz和7Hz的正弦指令信号。相应的PTC前馈控制器的期望状态分别为

分别利用本文方法和文献[10]给出的两种控制方法进行仿真,得到动态跟踪误差如图6所示。对比两组曲线中可以看出,本文设计的鲁棒完全跟踪控制器有着更高的跟踪精度,对模型摄动和摩擦扰动具有更好的抑制能力。
4 结论
本文将PTC,DOB和PID三种控制方法有机的组合在一起,提出了一种鲁棒完全跟踪控制器设计方法。与已有控制方法的对比仿真结果充分说明了本文所提控制方法在跟踪精度,干扰抑制等方面的优越性。本文的研究虽然是围绕飞行仿真转台展开的,但是所提出的设计方法并不具有特殊性,完全适用于其它系统,只要能够为所设计的系统提供期望状态作为输入,并且控制周期可根据指令更新周期和系统阶数进行调整,就可以应用本文所提的控制方法改善系统动态性能。
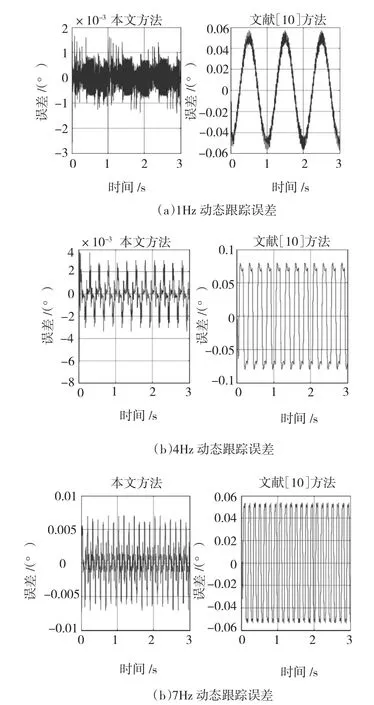
图6 不同频率正弦指令动态跟踪误差比较Fig.6Thecomparisonofthedynamictracking errorforthesinesignalwith differentfrequency
[1]TOMIZUKAM.Zerophaseerrortrackingalgorithmfordigitalcontrol[J].ASMEJournalofDynamicsSystem,Measurementand Control,1987,109(1):65-68.
[2]FUJIMOTOH.Generalframeworkofmultiratesamplingcontrol andapplicationstomotioncontrolsystems[D].Tokyo:TheUniversityofTokyo,2000.
[3]FUJIMOTOH,FUKUSHIMAK,NAKAGAWAS.Short-span seekingofHDDbyvibrationsuppressionPTCbasedoncontrollablecanonicalrealization[C]//The2005IEEE/ASMEInternationalConferenceonAdvancedIntelligentMechatronics,July24-28,2005,Monterey,USA.2005:7-12.
[4]FUJIMOTOH,FUKUSHIMAK,NAKAGAWAS.Vibrationsup-pressionshort-spanseekingofHDDwithmultiratefeedforward control[C]//Proceedingsofthe2006AmericanControlConference,April4-6,2006,NewYork,USA.2006:582-587.
[5]NAKAIT,FUJIMOTOH.Harmoniccurrentsuppressionmethod ofSPMmotorbasedonrepetitiveperfecttrackingcontrolwith speedvariation[C]//Proceedingsofthe34thAnnualConference ofIEEEIndustrialElectronicsSociety,November10-13,2008,Piscataway,USA.2008:1210-1215.
[6]SAKATAK,FUJIMOTOH.Perfecttrackingcontrolofservomotor basedonprecisemodelconsideringcurrentloopandPWMhold[J].ElectricalEngineeringinJapan,2009,166(4):64-72.
[7]MIYAZAKIT,OHISHIK,SHIBUTANII,etal.Perfecttracking controlbasedonpredictionofreferenceforhighspeedopticaldisc system[C]//Proceedingsofthe33thAnnualConferenceofthe IEEEIndustrialElectronicsSociety,November5-8,2007,Taipei,China.2007:345-350.
[8]BAANGD,CHOIJY,SHIMH,etal.Perfecttrackingcontrol forlinearsystemswithstateconstraint[J].InternationalJournal ofControlAutomationandSystems,2007,5(2):218-222.
[9]LIF,ISHIHATAK,LUJ,etal.Perfecttrackingcontrolusing multiratecontrolinmagneticlevitationsystem[C]//2005IEEE InternationalSymposiumonCircuitsandSystems,May23-26,2005,Kobe,Japan.2005(5):4851-4854.
[10]吴云洁,田大鹏,刘佑民.飞行仿真转台的完全跟踪控制[J].控制理论与应用,2011,29(2):414-420.
WUYunjie,TIANDapeng,LIUYoumin.Perfecttrackingcontrol forflightsimulator[J].ControlTheory&Applications,2011,29(2):414-420.
[11]熊田忠,梅志千,郑洁.基于干扰观测器的交流速度伺服系统的干扰抑制[J].中国电机工程学报,2005,25(12):229-234.
XIONGTianzhong,MEIZhiqian,ZHENGJie.DisturbanceobserverbaseddisturbancerejectioninACspeedservosystem[J].ProceedingsoftheCSEE,2005,25(12):229-234.
[12]LEEHS,TOMIZUKAM.Roubustmotioncontrollerdesignfor high-accuracypositioningsystems[J].IEEETransactionson IndustrialElectronics,1996,43(1):48-55.
[13]CHOIY,YANGK,CHUNGWK,etal.Ontherobustnessand performanceofdisturbanceobserversforsecond-ordersystems[J].IEEETransactionsonAutomaticControl,2003,48(2): 315-320.
[14]KEMPFCJ,KOBAYASHIS.Disturbanceobserverandfeedforwarddesignforahigh-speeddirect-drivepositioningtable[J].IEEETransactionsonControlSystemsTechnology,1999,7(5):513-526.
[15]刘毛.机电位置伺服系统鲁棒控制器设计及实验研究[D].哈尔滨:哈尔滨工业大学,2010.
(编辑:张诗阁)
Disturbanceobserver-basedrobustperfecttracking controlforflightsimulator
CHENSong-lin,SHANMei-lin,WANGLi-bin
(ControlandSimulationCenter,HarbinInstituteofTechnology,Harbin150001,China)
:Tomeettherisingperformancesrequirementsofflightsimulator,anovelrobustperfecttrackingcontrol(PTC)strategywasproposed.OnaccountofthePTC’sdependenceonaccuracyofthemathematicalmodelsofthecontrolledplant,thedisturbanceobserver(DOB)wasintroducedtoeliminatethe modelperturbationandtheexternaldisturbancesothattheinput-outputcharacteristicsoftheplantisalwaysclosetothenominalmodelwithinthegivenfrequencyband.Thesimulationresultsshowthatthe proposedstrategyisofgoodtrackingperformanceeventhoughintegratedwiththesimplePIDclosed-loop controller.TheconcretedesignmethodofPTCandDOBwereprovidedindetail.Thesimulationscomparedwiththeexistingmethodwereconducted.Theresultsindicatethattheproposedmethodhasbetter trackingperformanceandstrongercapabilityondisturbanceattenuation.
flightsimulators;perfecttrackingcontrol;disturbanceobserver;PID;disturbanceattenuation
10.15938/j.emc.2015.01.017
TP273
A
1007-449X(2015)01-0113-06
2014-03-07
国家自然科学基金(61021002,61174202)
陈松林(1976—),男,博士,副教授,研究方向为鲁棒控制,先进机电伺服系统;
单梅林(1988—),男,硕士,研究方向为伺服系统的鲁棒控制;
王丽斌(1988—),男,博士研究生,研究方向为机电伺服系统。
陈松林
