基于Simulink的连续搅拌反应釜的建模与仿真
2015-02-23何美霞杨友平长江大学电子信息学院湖北荆州434023
何美霞,杨友平 (长江大学电子信息学院,湖北 荆州 434023)
基于Simulink的连续搅拌反应釜的建模与仿真
何美霞,杨友平(长江大学电子信息学院,湖北 荆州 434023)
[摘要]作为化工过程中的重要设备,连续搅拌反应釜(CSTR)决定了化工产品的质量和生产能力。针对非线性的CSTR系统,基于Simulink平台采用模块组建和S-Function这2种方式创建其单输入单输出状态空间仿真模型。取系统的一个稳定工作点,在仿真时间的不同时段,利用动态矩阵控制(DMC)算法,通过改变冷却剂温度实现对系统出口物料温度的控制。利用该模型可模拟冷却剂温度对出口物料温度的影响。仿真曲线验证了该模型的正确性与可行性,可用于连续搅拌反应釜系统中实现动态仿真。
[关键词]连续搅拌反应釜;动态矩阵控制;Simulink;建模;仿真
连续搅拌反应釜(CSTR)是化工生产过程中完成聚合反应过程的常用设备之一。由于CSTR具有投资少、热交换能力强及可保证产品质量稳定等特点,因此在化工产业有广泛的应用及较大的研究价值[1]。Simulink仿真系统是Matlab最重要的组件之一,能够使用户和系统交互进行动态系统建模、仿真和综合分析[2]。针对CSTR系统,笔者在进料流量、温度和浓度等恒定的状态下,得到了非线性单入单出状态空间模型;利用模块组建、S-Function构造CSTR仿真模型;在仿真时间的不同时段,利用动态矩阵控制算法,通过改变冷却剂温度实现了对系统出口物料温度的控制。
1CSTR的状态空间模型
在CSTR反应器中,物料以一定浓度CAf、温度Tf和流量q进入容积为V的反应器,在反应器能发生放热不可逆反应,出口物料的相应量分别为CA、q、T,冷却剂的流量为qc、温度为Tc,CSTR的结构及参数如图1所示。取CSTR模型的2个状态变量反应物浓度CA和反应釜内温度T,控制变量为冷却剂的温度Tc,即通过Tc来控制CA和T,达到设计的控制目标[1]。

图1 连续搅拌反应釜的结构及参数
根据反应物料平衡算式和能量守恒定律,得到如下的状态空间模型[1,3]:

(1)
式中,参数的物理意义及取值见表1。

表1 CSTR模型中各参数的物理意义及取值


(2)
2Simulink建模
在Simulink软件中进行系统仿真可以省去许多繁琐的编程工作。Simulink模型可以让用户知道具体环节的动态细节,清楚地了解到系统各组建、各子系统、各分系统之间的信息交换。下面分别介绍基于Simulink模型库中的基本模块建模方法和用户定义函数中的S-Function建模方法。
2.1 利用模块搭建CSTR仿真模型
打开软件Matlab R2010b(Matlab 7.11),启动Simulink。在“Commonly Used Blocks” 、“Math Opertions”和“Signal Routing”模块库中选定“Constant”、“In1”、“Integrator”、 “Add”“Divide”、“From”及“Goto”等模块。基于式(2),搭建如图2所示的Simulink仿真模型。

图2 非线性CSTR仿真模型
对图2中的内容进行封装,形成CSTR子系统,封装好的CSTR仿真模型便于后续整体仿真的调用。
2.2 基于S-Function构造CSTR仿真模型
由式(2)可知,控制对象的数学模型是非线性的。此时利用Simulink中的“User-Defined Functions”中的S-Function模块按以下步骤可构造CSTR仿真模型。
步1初始化程序:
function[sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates= 2;
sizes.NumDiscStates= 0;
sizes.NumOutputs= 1;
sizes.NumInputs= 1;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0= [0;0];str =[];ts =[0 0];
步2状态方程程序:
function sys = mdlDerivatives(t,x,u)
sys=[0.5-x(1)-7.2*1010*exp(-8750/(x(2)+350))*(x(1)+0.5);
-x(2)+1.2*7.2*1014/239*exp(-8750/(x(2)+350))*(x(1)+0.5)+500/239*(u-x(2)-12)];
步3输出方程程序:
function sys = mdlOutputs(t,x,u)
sys = x(2);
步4步1~步3在S-Function模块中实现,保存为CSTR.m文件。
3仿真效果分析
动态矩阵控制(DMC)是一种基于非参数模型的控制算法,包含了预测模型、滚动优化、反馈校正3个要素,在处理非线性问题时存在一定的优势,其算法的具体内容可参看文献[5,6]。为了采集CSTR系统的历史输入输出信息,将Simulink中的Random Number模块作为CSTR模型的随机输入产生随机输出,如图3所示。将Workspace中的up、yp变量保存到yp_up.mat文件里作为CSTR历史信息随时调用。
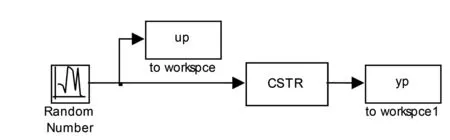
图3 获取CSTR历史信息的模型
利用DMC控制器对CSTR仿真模型控制,建立图4所示的系统仿真框图。图4中CSTR模块可采用上述建立的2类模型中的任意一个。

图4 CSTR系统控制仿真模型
设定控制目标值为:0~5s, yss=347K;5~10s,yss=353K;10s后,yss=350K。预测控制的相关参数值分别设为:模型时域N=100,预测时域P=20,控制时域M=5。采用图4的模型仿真得到如图5所示系统的输入、输出曲线。

图5 N=100、P=20、M=5时仿真效果图
从图5中可看出,CSTR系统的输入在仿真的开始阶段有较大的变化,这是因为冷却剂刚好与系统内的物料混合。此时系统的输出,即物料的输出温度受冷却剂温度控制,在12s时恢复到了原平衡态。
改变预测控制的N、P、M参数值,系统的输入、输出实时仿真图如图6~图8所示。从图中可以看出,当参数N的数值确定后,改变P、M参数的数值,系统的输入和输出特性几乎保持不变。而当参数P、M数值确定后的,改变N参数的数值,系统的输入和输出特性发生较大变化,不仅系统的超调增大,而且系统达到设定值的时间也变长。
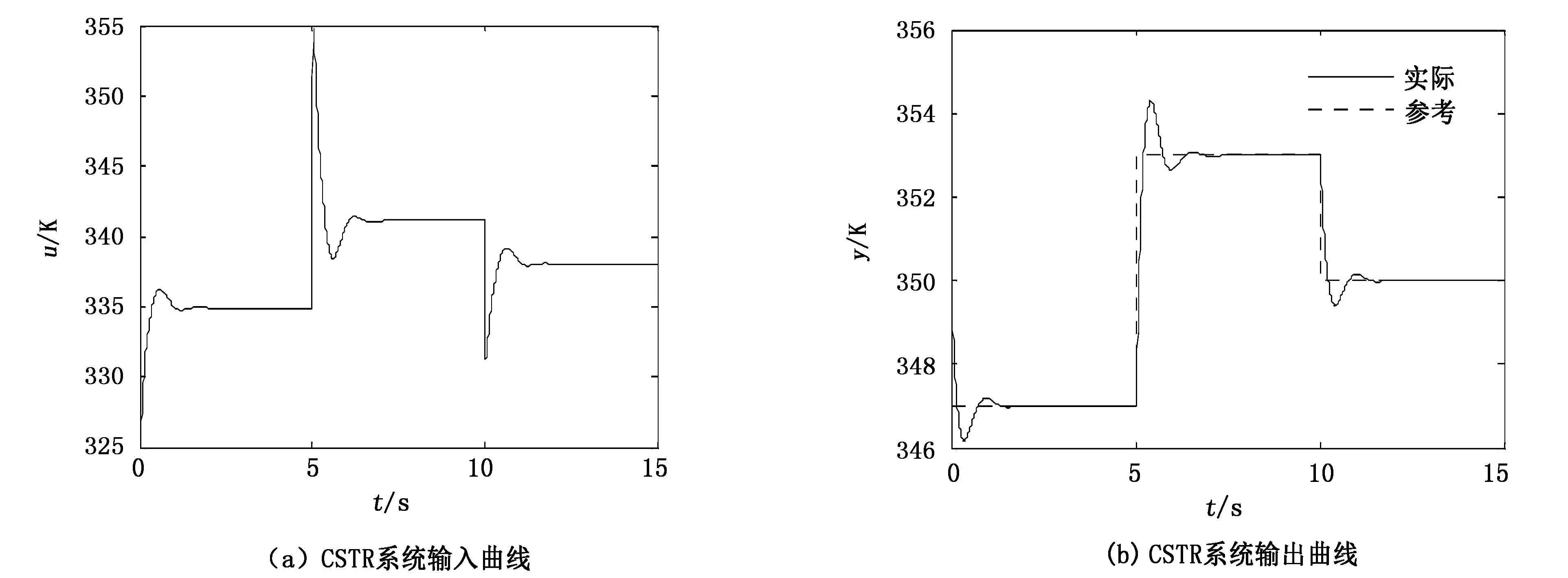
图6 N=100、P=50、M=5时仿真效果图

图7 N=100、P=20、M=15时仿真效果图

图8 N=50、P=20、M=5时仿真效果图
4结论
1)针对非线性CSTR系统,在进料温度Tf,流量q和浓度CAf等恒定的状态下,通过改变冷却剂的温度Tc来控制出口物料温度T,最终得到了单入单出状态空间模型。
2)基于Simulink平台,采用“Constant”、“Integrator”、 “Divide”等模块和S-Function这2种定义方法构造了CSTR仿真模型。
3)取CSTR系统的一个稳定的工作点,利用DMC算法,通过改变系统冷却剂温度实现了对系统输出温度的控制。仿真结果验证了所建仿真模型的正确性及可行性。
[参考文献]
[1]满红.CSTR过程的模型辨识及其非线性预测控制方法研究[D].大连:大连理工大学,2014.
[2]周建兴,岂兴明,矫津毅,等.Matlab从入门到精通[M].第2版.北京:人民邮电出版社,2012.
[3]于占东.基于智能自适应控制的腈纶聚合过程控制系统研究与应用[D].哈尔滨:哈尔滨工业大学,2005.
[4]Ding B. Constrained robust model predictive control via parameter-dependent dynamic output feedback [J]. Automatica, 2010, 46(9):1517~1523.
[5]丁宝苍.预测控制的理论与方法[M].北京:机械工业出版社,2008.
[6]丁宝苍,罗小锁,罗霄,等.先进控制理论[M].北京:机械工业出版社,2010.
[编辑]洪云飞
[引著格式]何美霞,杨友平.基于Simulink的连续搅拌反应釜的建模与仿真[J].长江大学学报(自科版),2015,12(28):21~25.
[中图分类号]TP273
[文献标志码]A
[文章编号]1673-1409(2015)28-0021-05
[作者简介]何美霞(1986-),女,硕士,助教,现主要从事预测控制、过程控制的仿真方面的教学与研究工作;E-mail:1131366980@qq.com。
[基金项目]湖北省教育厅科研计划资助重点项目(D20111302)。
[收稿日期]2015-06-19
