凸轮恒磨除率磨削的转速曲线优化
2015-02-22刘艳韩秋实李启光彭宝营
刘艳,韩秋实,李启光,彭宝营
(北京信息科技大学 机电工程学院,北京 100192)

凸轮恒磨除率磨削的转速曲线优化
刘艳,韩秋实,李启光,彭宝营
(北京信息科技大学 机电工程学院,北京 100192)
摘要:凸轮是复杂的非圆零件,加工过程中,瞬时速度和加速度剧烈变化会降低加工品质。推导了恒磨除率变速磨削数学模型。基于恒力磨削的思想,得到了凸轮C轴变速恒磨除率公式。在此基础上,运用最小二乘法对凸轮轮廓数据进行多项式拟合,得到平滑的凸轮转速曲线和砂轮进给速度曲线。仿真结果表明,该方法能够使磨除率保持近似恒定的同时,还得到平滑的旋转轴转速曲线,并大幅减小C轴的加速度,从而提高凸轮轴磨削精度。
关键词:凸轮;恒磨除率;最小二乘法;速度优化
0引言
凸轮磨削是一种复杂的非圆磨削,除磨削基圆部分与普通的外圆磨削加工状况一样,其他部分的磨削条件是不断在变化的。磨削凸轮一周的顺序为:“基圆-升程-桃尖-顶圆-回程-基圆”。采用恒角速度磨削凸轮时,磨削深度相同时,由于凸轮极径的变化引起磨削点线速度变化,使得接触弧长不同,从而金属切除率和磨削力除基圆部分恒定外其他部分的磨除率和磨削力不断变化,磨除率和磨削力变化会对凸轮加工表面品质产生较大影响。理论上,恒线速度磨削加工,磨削力比较平稳,可提高工件磨削加工精度和工件磨削表面品质。但实际生产加工中,恒线速度加工复杂的联动轴运动,引起瞬时速度和加速度剧烈变化。
北京信息科技大学提出了基于恒磨除率的恒线速磨削加工数学模型,采用三次样条曲线拟合方法,得到波动的速度曲线[1-3];湖南大学采用三次样条曲线拟合方法对工件旋转速度优化,提出了近似的恒线速控制方法,通过控制磨削点加速度对速度进行优化[4-5]。基于恒磨除率变速磨削模型运用最小二乘法拟合多项式并求导,计算得到波动较小的C轴转速和砂轮架进给速度。使工件在不同的磨削点处,工件转速不同,凸轮单位时间内磨削的弧长基本保持不变,以保证在磨削凸轮一周的过程中,金属磨除率基本保持不变,且磨削力变化不大,减少凸轮轮廓的加工表面纹波和烧伤。
1凸轮恒磨除率磨削的数学模型推导
凸轮轮廓数据的表达方式有两种分别为:凸轮轮廓曲线数据和升程数据。采用凸轮轮廓曲线数据并由几何关系直接确定恒磨除率变速磨削数学模型。已知凸轮的型线方程ρ=ρ(φ),将凸轮轮廓的极坐标转化为直角坐标。
根据坐标旋转公式,当凸轮转过时,凸轮轮廓型线方程为:
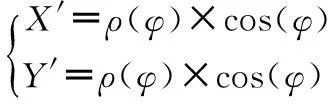
(1)
根据坐标旋转公式,当凸轮转过θ时,凸轮轮廓型线方程为:

(2)
由式(2)得到在直角坐标系中凸轮轮廓的离散值,为最小二乘法拟合多项式的原始数据。
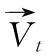

图1 凸轮磨削模型

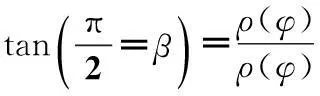
(3)
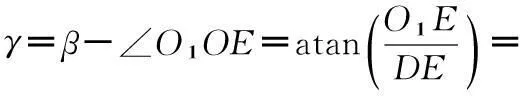
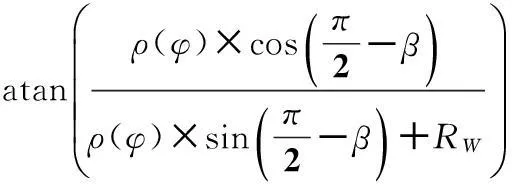
(4)
1.1 单位时间凸轮磨削弧长的计算
磨除率是指单位时间内磨除的弧长、磨削深度ap和凸轮宽度b的乘积。磨削深度ap和凸轮宽度b为磨削加工前已确定的值,磨除率与单位时间内磨除的弧长成正比关系,因此恒磨除率是近似指单位时间内磨削弧长恒定。凸轮单位时间磨削的弧长公式如下[1]。
1.2 基于恒磨除率的凸轮转速公式推导

(5)
凸轮宽度b和磨削深度ap均为固定不变量,基圆部分单位时间内磨削弧长恒定,故基圆部分磨除率也为定值,设为K,则K=R0ω0,令凸轮其余部分磨除率也为K,即保证凸轮全部轮廓磨削的恒磨除率。由式(3)知:

则除基圆部分外凸轮的转速ωφ的公式为:

(6)
1.3 凸轮磨削点线速度和砂轮架移动速度公式推导
凸轮轮廓的磨削加工是由凸轮c轴和砂轮架x轴的联动实现的。因此,凸轮磨削加工过程由切入和联动两部分构成,要实现联动必须满足条件式(7),沿凸轮极径方向速度合成为零,否则会产生“过切”或者“切不到”的现象。
Vtsinβ-Vxcosα=0
(7)
由图1知,实现联动加工时,凸轮上磨削点的线速度Vc、磨削点处的切线速度Vt和砂轮架进给速度Vx满足如下关系:

Vc=Vtcosβ+Vxsinα
因此,由式(7)知A点瞬时线速度为:

(8)
将已求的β和α带入求的砂轮架移动速度公式:

(9)
2凸轮转速曲线优化
凸轮恒磨除率磨削的加工方法虽然能有效提高加工精度,但随着极径的变化磨削点线速度也不断变化,容易引起联动轴x轴的加速度过大,机械系统和伺服系统的响应不能满足要求,可能引起冲击、震颤等降低凸轮轮廓表面品质。另外,由恒磨除率变速磨削模型知,凸轮上单位时间内磨削弧长恒定只是近似的恒金属切除率,磨削量与各点的曲率半径有关,曲率半径越大磨削量越大[7],而凸轮顶圆部分轮廓曲率较大,磨削加工时需要适当降低顶圆部分转速才能使磨削更充分。为了使加工曲线既符合机床机械系统和伺服系统的响应要求,又满足充分磨削和理论曲线的基础上对凸轮转速曲线进行优化[8-10]。
2.1 最小二乘法原理
已知的凸轮轮廓数据是离散值,从恒磨除率变速磨削的数学模型可以看出,砂轮架的移动速度Vx和凸轮除基圆部分的转速的计算与导数的算法ωφ有关,合理的算法可以避免计算误差累积引起Vx和ωφ的波动,所以本文在保证恒磨除率的同时对凸轮c轴转速曲线进行光顺,来提高磨削工件的表面品质。
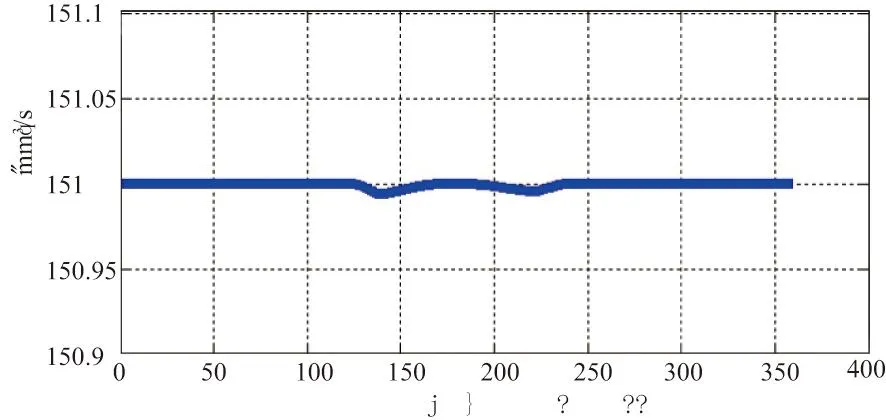
最小二乘法拟合凸轮轮廓曲线多项式。最小二乘法是已知一组数据(xi,yi),(i=1,2,…,n),求参数a0,a1,…,am(m 利用高斯消元法求解,求得多项式S(x)=a0,a1x+…+anxn,对其进行求导并带入xi的值,方可求得导数,并计算凸轮转速和砂轮架移动速度。利用最小二乘法不需要通过所有已知点,只要求各点出的误差平方和最小,明显优于三次样条拟合,最小二乘法可以滤除原始数据中的测量误差,即反应了凸轮轮廓的总体特性,又滤除了局部大的波动和函数逼近的特性。 以车磨复合机床上磨削加工为例,对恒磨除率变速磨削加工进行分析。凸轮的基本数据为:基圆半径15.1mm,最大极径为20.0775mm,极角极径是由L_2000系列凸轮轴检测仪采集得到,共采样360个点,采集间隔为一度,砂轮半径500mm。运用MATLAB软件对凸轮轮廓数据进行8段9次多项式拟合,求得8个S(x)的9次多项式,并分别对其求导。将结果带入式(4)和式(6),计算出凸轮转速曲线砂轮架移动速度曲线,如图2、图3和图4为优化后磨除率变化曲线。 图2 恒磨除率变速磨削c轴速度图 图3 恒磨除率变速磨削优化后砂轮架速度及加速度图 图4 恒磨除率变速磨削转速优化后磨除率图 3结论 推导了基于恒磨除率变速磨削的数学模型,利用最小二乘法对凸轮轮廓数据进行多项式拟合求导,对凸轮变转速曲线和砂轮架移动速度曲线进行了优化,既保证了磨除率恒定又求得了波动较小的凸轮转速曲线和砂轮架移动速度曲线。结果显示,最小二乘法优化凸轮磨削的动态特性曲线,有效的减小了联动轴加速度的跳动。 参考文献: [1] 王娟. 凸轮轴数控磨削加工过程动态优化仿真的研究及软件开发[D]. 长沙:湖南大学,2009. [2] 曹德芳. 凸轮轴数控磨削工艺智能应用系统的研究与开发[D]. 长沙:湖南大学,2012. [3] 涂志. 数控凸轮轴磨床数控加工软件的理论分析与程序设计[D]. 北京:北京机械工业学院,1998. [4] 王红军,韩秋实,许宝杰,等.数控凸轮轴磨床加工过程的仿真软件设计[J].机械工程师,1999,2:18-19. [5] 韩秋实,王红军,许宝杰,等.数控凸轮轮轴磨床的加工仿真原理及软件研制[J].制造技术与机床,2000,8:37-39. [6] 郭力. 切点跟踪磨削法高速磨削凸轮轴[J]. 湖南文理学院学报,2010, 22(2):54-60. [7] 曹德芳,邓朝晖,刘伟,等. 凸轮轴磨削加工速度优化调节与自动数控编程研究[J]. 中国机械工程,2012(23):2149-2154. [8] 李勇. 影响凸轮轴磨削若干因素加工精度[D]. 武汉:华中科技大学,2004. [9] 邓朝晖,王娟,曹德芳,等. 凸轮轴磨削加工过程的动态优化和仿真[J]. 湖南大学学报,2009,36:21-25. [10] 同济大学教研室.高等数学[M].北京:高等教育出版社,2002,38(8):68-73. Speed Curve Optimization of Constant Removal Rate of Cam LIU Yan,HAN Qiu-shi,LI Qi-guang,PENG Bao-ying (College Of Mechanical Engineering, Beijing Information Science & Technology University, Beijing 100192,China) Abstract:Cam is a non-circular parts. The dramatic change of instantaneous speed reduces the processing quality . This paper deduces variable speed grinding mathematical model, based on the constant grinding rate. The variable-speed grinding removed constant rate figure of the cam C shaft is obtained based on the idea of constant force grinding. On this basis, it uses the least square method to do the polynomial fitting of the cam profile data and get the speed curves of smooth cam operation and grinding wheel feeding. The simulation results show that the method can be used to make the grinding rate approximately constant and get the smooth rotation speed curve, and the C axis acceleration is reduced greayly, thus improving the cam grinding precision. Keywords:cam;grinding removal constant rate;least square method;speed optimization 收稿日期:2014-11-07 中图分类号:TH132.47;TG580.6 文献标志码:B 文章编号:1671-5276(2015)02-0026-04 作者简介:刘艳(1988-),女,河南洛阳人,硕士研究生,研究方向:智能化与数字化控制。 基金项目:国家自然基金资助项目(51375056);北京市自然科学基金重点项目(KZ201211232039);北京市高等学校人才强教(PHR201106132)资助项目资助
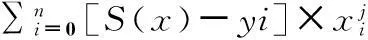

2.2 凸轮磨削的动态特性曲线优化