对高等数学课程实施研究型教学法的探析

李小梅

(浙江科技学院 理学院,杭州 310023)



浙江科技学院学报,第27卷第1期,2015年2月

Journal of Zhejiang University of Science and Technology

Vol.27 No.1, Feb. 2015

对高等数学课程实施研究型教学法的探析

李小梅

(浙江科技学院 理学院,杭州 310023)

摘要:研究型教学法虽然已在很多高校中普遍展开,但如何更好、更有效地实施仍值得探索。由此,对在本科院校重要基础课的高等数学课程中实施研究型教学法进行了剖析，并以实例详细阐述了如何结合高等数学课程生源面广、内容多、课时少、难度系数大、大班课堂教学等特点进行有效教学的具体思路与步骤。同时,结合社会发展新形势下的教学改革思路，以及研究型教学的特定内涵,提出了在研究型教学改革中的一些新模式和新方法。

关键词:高等数学;教学改革;研究型教学;课堂教学

研究型教学是以培养学生创新能力为目的,从研究的实际背景和问题出发,创设问题的情境,形成学生在教师的引导下,立足所学,确定课题,通过观察、实验、分析、归纳、猜想、论证、社会实践等方式进行探究性学习的一种教学法。从问题的提出,方案的设计与实施,结论的得出和论证,整个过程构造了创造性思维活动的一种探究性信息运动系统。在整个运动系统中，各个子系统之间优势互补、协同发展,呈现出非线性的相互、相关作用，具有主体性、多元性、合作性、研究性、开放性和创新性等特点。所以,研究型教学法在很多高校中普遍展开,深受广大教师的喜爱,并在教学改革与实践中取得了一定的成效。

但随着教学改革形势的不断深入发展,课堂教学也蕴含着新的要求，出现了新的问题。因此，探讨研究型教学方法的改革与实践应是经常的、长久的，它不是一朝一夕的事,是一个持续发展的过程[1]。实际上,在高等数学课程中实施研究型教学法时就经常会遇到这样一些问题:1)在创设研究探讨的问题时,怎样结合数学教学特点,更好地融入数学本身的元素,形成学生观察、实验、分析、归纳、猜想、论证等探索性研究的习惯;2)高等数学课程具有内容多、课时少的特点,怎样巧妙地利用研究型教学的主体性、多元性、合作性、研究性、开放性和创新性等特点，探索解决好这一困扰;3)高等数学是大一新生必学的重要基础课,他们仍带着中学数学学习方法的烙印，如何寻找出学生在研究探索过程中尽快适应高等数学学习的方法;4)高等数学课程大都是大班上课,学生人数多,接受知识的程度参差不齐,又怎样去更好地组织起研究型教学中的有效教学,使之不流于形式?等等。若能处理和解决好这些问题,必将有助于高等数学课堂教学中的研究型教学法的实施。

1融合高等数学多方面元素,丰富研究型教学多层面的活动

美国国家科学教育标准认为,在研究型教学中,研究探索的过程是多层面的活动。包括观察、提出问题,通过浏览书籍和其他信息资源发现、调查、研究问题,以及对问题进行批判、逻辑推理、评价、解释、预测,甚至可以考虑问题的替代、转化等。高等数学课程正是具有这些多方面、多功能的效应。高等数学本身的知识体系及结构充满着内在的逻辑性、严谨性、确定性或不确定性乃至抽象性等组成元素。而对数学知识的分类、整理、综合、构造,不同层次的公理体系和形式体系的形成,又处处蕴含着高等数学学习的数学化元素[2]。特别是数学对人的世界观、思维品质、能力培养的影响,以及与其他学科的交融性、渗透性,更是具有无可厚非的多元性元素。高等数学的这些元素构造了研究型教学多层面活动的丰富内涵,若能巧妙地融合在研究型教学中,将可使学生在学习高等数学课程中取得事半功倍的效果。

案例:定积分概念的引入

在引入定积分概念之前,先讲述一个学生儿时就听过的一个故事:《曹冲称象》,它的根本实质是“化整为零”,然后再“积零为整”:

教师问:有谁知道《曹冲称象》的故事?——让学生叙述;

教师问:这个故事说明什么?——学生有多种回答,有的说曹冲从小就聪明,但接近实质的很少;

教师问:这个故事中的处理方法是什么？——学生逐渐接近实质,把大象重量转化成小石块的重量即“化整为零”,然后将小石块重量逐块相加得到大象重量即“积零为整”;

教师问:这种处理方法能否推广?——学生一致回答“可以”;

教师问:我们现在计算一个曲边梯形的面积,能否用《曹冲称象》的方法来计算？——学生大多数说应该可以,但不知道怎样去计算。

这时,可让学生自己看书10 min后通过教师的指导在黑板上演绎得出一个和的极限。并总结计算得出分析问题的四步骤:分割、计算微元、求和、取极限。接着,让学生按此步骤探讨求变速直线运动路程的问题,也得到这样的形式:和的极限。

教师问:还有哪些“变”的问题可以这样处理,为什么？——学生踊跃发言,各执己见,有对,也有错。(这里只限学生课内讨论5 min,布置课后继续讨论,要求拿出书面意见,为下一章《定积分的应用》打下“埋伏”。构成分析的延续。)

教师问:2个问题都得到一个相同的形式,怎样描述?——由此引出定积分的概念。

在这里,充分利用数学知识的发现、推理、归纳、类比、延伸等数学分析的元素，以一小典故的引入逐渐指导学生发现问题,掌握规律,再举一反三,进行推广。这种通过选择简单、直观、能说明问题的应用实例，引入数学概念、思想和方法,不仅可使数学教学新颖有趣,也可使学生易于接受[3]。整个过程让学生感受到了对问题的分析、评价、预测、探究的熏陶。

实际上,在数学中归纳和类比是两种应用极广的推理分析。归纳体现了发现、观察、总结问题的过程。类比则是从各事物已有的共同属性入手,联想出可能的相似之处的过程。它们构造了数学知识发现的两种重要元素。若能在研究型教学中很好地融合这样的数学元素,则可以让学生在学习新知识时注意观察实验、归纳类比、深化拓展、触类旁通、开阔思路。

案例:不定积分的计算

归纳总结得出:若f(x)中有xn和xn+1,那么令u=xn+1,凑du。

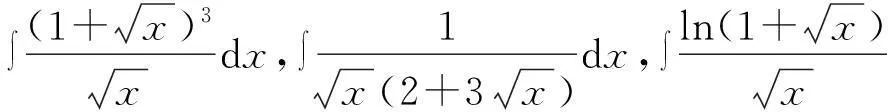
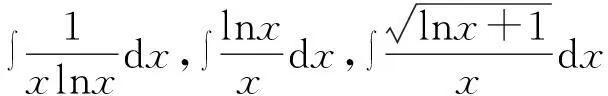
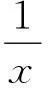
然后由上面这一类题目,总结归纳得出不定积分计算的常用配元表。这里,既让学生对所学知识加深印象,也让学生学到归纳类比的学习方法。可见，在研究型教学中结合数学化元素进行教学,充实了研究型教学多层面的活动。不仅让学生学到知识,还可让学生提高学习技能。

2结合研究型教学特点,消除高等数学内容多、课时少的困扰

高等数学内容多、课时少，经常困扰着授课教师。有的教师为了赶进度对一些知识的学习点到为止,甚至放弃。而利用研究型教学的多元性、主体性、合作性、研究性、开放性和创新性等特点,可以缓解此矛盾。

2.1　研究型教学“多元性”的应用

数学中的公式、定理都有着丰富的发展渊源,与其他学科知识也有着各式各样的关联。利用研究型教学的多元性对知识点进行多方位、多角度的分析,让学生在分析过程中,将概念通过广褒事例,抓住共性,抽象得出,就可以加深对概念的理解,便于后续概念的应用，从而为课堂讲解节省时间。

案例:讲解导数的定义

教师先讲解完书上的例子:瞬时速度、切线斜率,得到2个问题的共性:所求量为函数增量与自变量增量之比的极限——引出导数概念。

再引导学生推广,类似问题还有:加速度等于速度增量与时间增量之比的极限,角速度等于转角增量与时间增量之比的极限,线密度等于质量增量与长度增量之比的极限,电流强度等于电量增量与时间增量之比的极限——丰富导数概念的广度。

然后进一步指引学生思考生活中导数的实际体现。例如汽车的车速表可以称为“导数的显示器”;又如一块凉的红薯被放进热烤箱,其温度T是时间t的函数T=f(t),那么f′(t)的含义是什么？——增进导数概念的深度。

这样,指导学生从多角度、多方位理解导数的概念,对后面导数的计算公式、导数的应用节省了讲授时间。

2.2　研究型教学“主体性”的应用

案例:章习题课的处理

首先，教师针对每章中心内容设定主题。如主题一——对本章知识的要点、注意点和关联等,进行归纳、综合、比较;主题二——对本章所讲述的习题类型、解题思路、方法等,进行分类、整理。

其次，由学生自行组织学习小组,对主题进行探讨,探讨的时间一般定于一周之内。探讨的方式:可利用课外时间,在小组内讨论或跨小组讨论;可在教室内,也在寝室内讨论;可在QQ内,也可在微信上探讨。不管用什么方式,小组研讨的图片,个人的书面小结(要求每个学生都写出书面小结)都需上交，以便于教师的指点,以及学生平时成绩的计入。

再则,对上交的个人书面小结进行评分。可先由各自小组长评,然后交换小组,由别的小组评,最后教师抽查、讲评。

这样，充分发挥了学生的主体作用,改变课堂教学中只教不用、只学不用的现状[4]，将部分习题课移到课外解决,既节省了课内学时,也加深了学生对知识点应用的理解。有些作业的批改、概念的引入,均可采用此法。

2.3　研究型教学“开放性”的应用

在研究性教学中,充分利用板书、多媒体、信息技术、网络平台、课内与课外参考书籍等多种教学手段,开拓探究途径,提高学生探究水准,对新知识的同化和顺应进行开放性教学,激发学生的求知欲[5]。其中,按照不同学生的个性构造学习方式的多样化，不仅是以数学知识的逻辑结构或形式化体系来呈现,也可以是大学生数学竞赛、数学实验和数学建模赛的个性化、多样化的呈现。保证在大面积学生学习取得进步的同时,激励一批数学优等生脱颖而出。对于学习内容则以不同形式进行多种方式的表达，不再只是呈现“是什么的知识”,而主要呈现“有什么意义与联系”性的知识、方法性知识。同时在教学中形成具有预测性和创见性的教学实施方案的粗略框架或粗线条的教学策略计划,并不对每一具体的小教学步骤作硬性规定。教学中留有一定的弹性空间,根据事物的不确定性和过程及非严格程序性,不断地变换思维,进行开放性的教学设计。使得在整个知识体系中呈现出知识间的联系性、层次性、科学性、抽象性、包摄性和概括性等多层含义。让学生多方面、多角度地接受知识的熏陶,从而拓宽其知识面,加快其学习进度。

在教学中，可实验如下一些开放性的教学模式(表1)。

表1　开放性教学模式的设置

上述开放性教学法,可依据教学内容的不同、教学对象水平的不同、教学时间长短的不同、教学情景的不同灵活选用;可选一种,也可以同时选多种。如此,既可提高学生学习知识的能力,也可加快教学的进展。由于其灵活性、包容性，消除了高等数学教学课时少的困惑。

人人都渴望拥有幸福的喜悦，享受幸福生活是人的本能。课程改革改革的教育理念更加强调教育对生命的关注，强调教育过程中的生命关注，作为一名教师，应该懂得运用积极心理学理论，关注学生的生命，重视学生在学习过程中让学生体验愉悦与成就，最终使学生获得生命的成长与幸福。

3高等数学课程的“入门”导引,是实施研究型教学法的首要问题

学习者性格、兴趣、动机和学习策略等非认知因素对接受新事物的挑战起着关键的作用。进入大学以后,无论是学习方法还是学习内容都进入了一个新的阶段。学习高等数学明确显示出与中学数学学习的差别。在高等数学课堂教学中，不仅知识容量较大，而且也不像中学教师那样课里、课外面面俱到地指点。而大多数新生上课时却仍带着中学学习方法的烙印,脑海中复印着中学教师谆谆的教诲。对高等数学的学习不知所措,无从下手。再者，进入大学后环境的改变对学生的学习心理也产生着一定的影响，大多数学生考取大学后,如释重负、学习懈怠、不知进取。那么，如何使大一新生尽快地适应高等数学课程学习,这是实施研究型教学法有待解决的首要问题。

3.1　处理好入门教学,抓住3个第“1”

第一个“1”:从高等数学的第1节课就进行交流。这时交流的是中学数学学习的思维方式与大学高等数学学习方法的衔接与对比。比如:中学研讨数学问题一般是在静止的状态下,而高等数学研究的数学问题一般是在变化的状态下,让学生从一开始就感受到学习高等数学必须要用变化的观念去学,从而为学好高等数学设下铺垫。如讲解“有限”与“无限”。在中学,从初等数学有限的角度来看,图1所示的两线段当然不一样长,但到了大学后,从高等数学无限的角度来看,可以证明这两条线段一样长。以此加深学生理解高等数学“变化”的概念,以吸引他们对学习高等数学的欲望。

图1线段的比较
Fig.1Comparison of line segments

第二个“1”:通过第1章的学习后,让学生感受到在课堂上的观察、思考、理解和接受知识,固然是学好高等数学的重要组成部分。但是，要深入了解和熟练掌握所学内容还必须经过课前预习、课后复习,以及自己看书等阶段。这些都是学生到了大学后首先面临的且必须经过的学习阶段。而且课内学习时间与课外学习时间比例最少为1∶2甚至1∶3等,才能把所要学的学科学好。比如:通过课外学习时间的弥补,学生会感觉到能听懂课内知识的百分比在逐渐提高:原来可以听懂课内知识的40%,通过一章学习后可以提高到60%,同时感觉自己可以将课内所学的知识举一反三了。这时,教师可明示:这表明你的自学能力提高了,你很棒。由此让学生感觉到自主学习能力提高的重要及自主学习能力提高的自信。

第三个“1”:通过第1学期的学习,让学生会用探究的学习方法去理解、掌握高等数学的学习。比如高等数学中定理、定义、公式大都是由条件及结论组成，教师在讲授时一般采用回忆旧知识,引出新问题,再推理得到新结论的方法。因此，让学生熟悉这一系列“探究”程序中的“规律”,自己试着用此“规律”检验自己推理的结论与预定结果是否一致,以提高自己的探究、创新能力。

这样，让学生从“1”开始就产生对学习高等数学的欲望,感受着自主学习能力提高的重要,学会探究、创新能力的培养，为学习高等数学扫除障碍。

3.2　以“趣、情、境”开启学生学习高等数学的大门,达到学生学习方法的初步掌握

趣,是指学生学习的兴趣。有了兴趣，学生就会主动与他周围的环境包括人和物发生相互作用,主动进行建构,真正的学习也就开始产生了。教学中可通过巧妙设疑提问等,引导学生观察、思考、动手操作来激发学生学习高等数学的兴趣。

情,是学生学习的情感。情感是学习高等数学的动力源泉,是学生在学习过程中发挥持久作用的前提条件。在教学过程中，教师可以培养与学生的良好人际关系,彼此相互鼓励、支持、协作以产生情感,共同享受学习和探究取得成功的喜悦。

境,是指学生学习的心境及学习的环境。好的学习心境是学习高等数学不可缺少的组成部分。引导学生勇于挑战,积极向上,构造一个“无拘无束”“自由翱翔”的良好学习情境。比如创设近似区域研讨式教学情境，对所学知识逐步搭建攀登的“脚手架”,形成学生攀爬与探索目标的“最近发展区”,激发学生探究兴趣,鼓励其探索信心,形成持续有效的研究性学习动力,使之能够尽快“入门”。

案例:讲解数列“ε-N”极限定义

于是，教师提问:数学上怎样描述n→∞时,xn→1?

让学生观察下式:

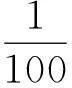
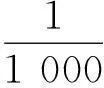
从以上过程可得:引进了ε后,刻划了在n无限增大的过程中,总可以找到时刻N,在这时刻后不等式|xn-a|<ε成立。由于ε的任意小,充分地体现了当n→∞时,xn无限接近于1。

让学生在一步步的理解之下,导出极限的“ε-N”定义。实际上“ε-N”定义历来都是教学难点。但由于构成了定义的近似区域,使得较难理解的极限“ε-N”定义变为较易理解。随后教师还可提出下列问题:1)N与任意给定的正数ε有关,N是否唯一？2)上面不等式能否取等号？3)ε能否取零？

由于构造了概念产生的背景、产生的推导,在实际应用等近似区域的情境,学生大都通过上述推导能够正确理解或回答。

4利用研究型教学的合作性,提高大班课堂教学的有效性

高等数学的教学主要采用班级授课制的大班教学。班级授课制有个基本的逻辑前提,即假设所有的学生都具有同样的学习能力,能够在同样的时间内以同样的速度学习同样的内容,并达到同样的要求。正是由于这种逻辑的假设,在实际教学中，教学进度、教学内容、教学策略、教学评价都是统一进行的,这种过于标准化、同步化的体制严重阻遏了学生的个性发展。那么，怎样对班级授课制的大班高等数学教学进行有效教学,使每个学生都有较好的收效呢？依据研究型教学,可以从实际背景和问题出发,创设问题的情境,确定课题,组织学生进行合作性学习。通过合作,当120个学生都坐在同一讲台下面对着教师组织的大班教学时,可以视同伴为一种学习资源,让具有不同特点的学生相互帮助、相互弥补、相互借鉴、相互争辩。逐渐积累经验,彼此接纳、取长补短,使部分“短路”的学生能够抓住问题的主干,而不至于纠结在某一个问题上“钻”不出来,从而达到全体学生共同进步的目的。当然，在合作学习中，对合作对象、合作时间、合作内容、合作形式的选择是至关重要的。对于合作对象,可以按近邻分组、寝室分组、成绩分组，合作时间可以按维持几分钟、维持一堂课、维持一章进行分组，合作内容可以按章节分组、习题分组、实践分组，合作形式可以问题合作、监督合作、写作合作，这样将极大提高大班课堂的有效教学。

比如课堂教学中的问题合作:构造以典型方法、典型例题、典型实践为中心的问题情景。分小组讨论,通过引导、类比、猜想、顺应、逆向思维，引起学生的认知、冲突、诱使。让学生自己提出问题,并对它产生探究的兴趣,明确探究的目标。然后分小组进行自由讨论,时间控制在10 min左右。讨论结束后,小组就讨论结果及感想发言,每个小组3~5 min;发言不拘形式,可一人,也可多人。最后教师进行讨论小结,注意对讨论中出现的共性问题和个性问题进行统筹指导。

案例:“问题合作”

在讲定积分应用时，教师提出下列问题进行讨论:1)定积分应用的原理;2)定积分应用的条件;3)定积分应用的类型;4)定积分应用的步骤;5)你能举出定积分应用的例子吗？

让相邻学生组成小组讨论10 min,并不要求所有问题均能回答;然后各组发言,其余小组可以进行补充。

又如课堂教学中的写作合作:对概念定理的推理,通过写作合作,展示学生在接触和学习某种事物的过程中,产生的感想和领悟到的东西,形成具有独到观点的小论文进行发表，以提高学生的分析及写作能力。

案例:“写作合作”

在学习中值定理时,由学生分组探讨并填写表2中的问题。

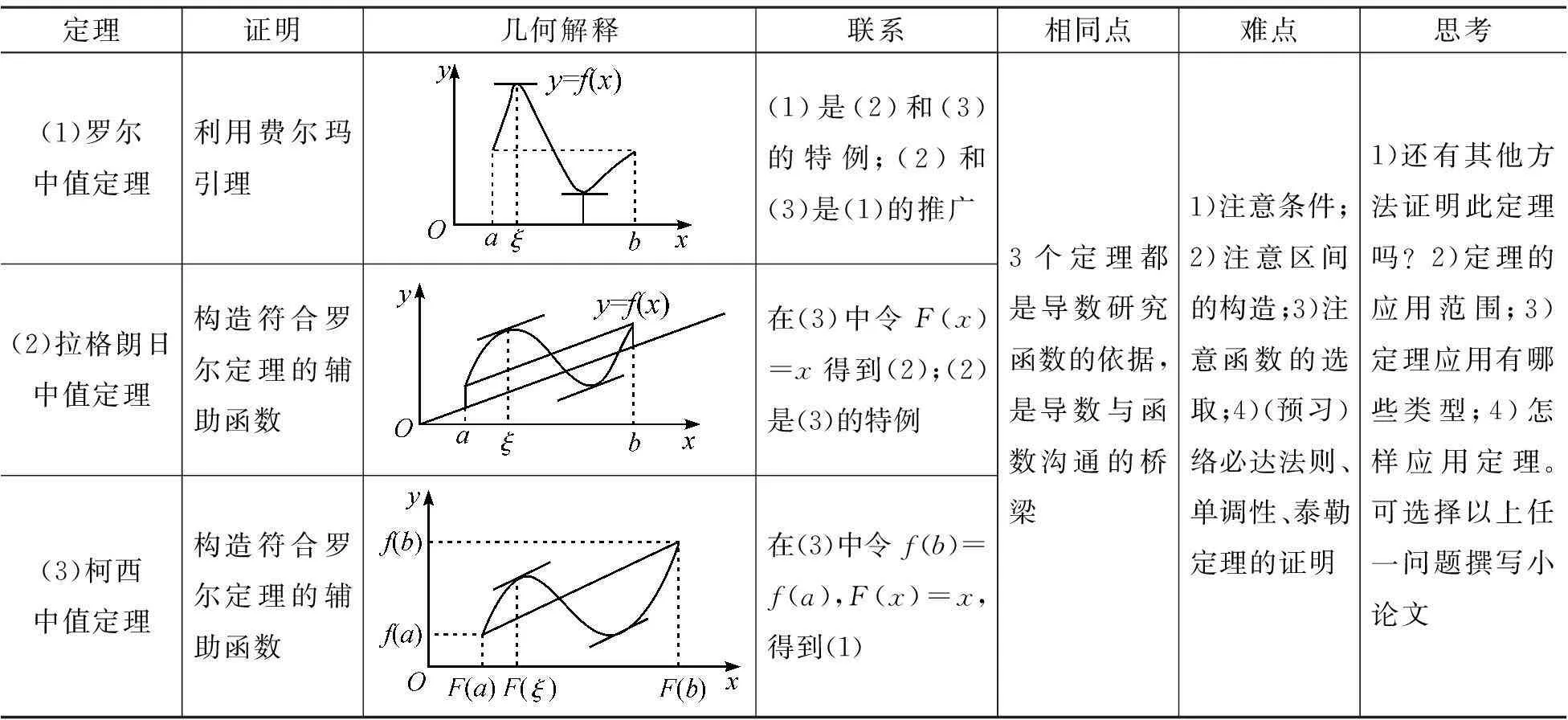
表2　中值定理综合分析

整个教学过程中通过合作学习,注重教学的多元化,注重学生主体作用的发挥,注重创造精神、独立精神和学生个性的发挥,注重知识体系间的纵向与横向联系，集多人智慧之精华,增己高质量之所学，使得大班课堂教学的有效性得以提高。

5结语

在中国,高等数学教学主要是以课堂教学为主，课堂教学效果的好坏,直接影响着学生的学习兴趣和学习态度,并最终影响学生学习的整体质量。增进大学数学课堂教学效果是大学数学教学体系改革的核心问题[6]。研究型教学方法是根据科学研究、实验、社会调查、技术开发等领域来设置的，教学形式多样,教学方法灵活。只要符合提出一发现一研究一解决问题的思路,达到学生的学习能力、思维能力、实践能力、创新能力等有所提高的目标,改革就具有初效。因此,在高等数学课堂教学中实施研究型教学,形成一个在动态中研究未知、发现问题、寻找有创意解决问题的研究型教学体系,构造一个满足个性化、多样化需求的学习探究性体系，对激发学生学习兴趣、学习信心,培养学生自我监督能力及自主学习能力,促使学生主动、有效地参与学习,亲历问题的探究过程是很有必要的。同时,结合新形势的要求,认真探讨研究型教学在高等数学课堂教学改革中出现的问题,对它进行调查、分析、适时解决，会更有利于高等数学课堂教学中研究型教学改革的顺利开展。

当然，随着网络、计算机的发展必将给高等数学课程实施研究型教学的改革与实践带来新的方法和技巧[7]。比如,现在由美国引进的慕课(MOOC)方式,将计算机的技术应用于学习过程,构成在线课程,推进了教育过程的开放;又比如“翻转课堂式教学模式”，学生是在课外完成知识的学习,课堂则为教师与学生交流的场所。而所谓“微课”教学模式则是以围绕某个知识点、教学环节,以视频为主要载体,从学生的角度开展的简短、完整的教学活动[8]。这些新模式的引进显然扩展了研究型教学改革的思路与实践，也极大地解决了高等数学内容多、课时少的矛盾，以及高等数学大班课堂教学“同一性”的困扰。当然，这些教学模式的实施还有待于进一步探索。

参考文献:

[1]吴云天,马菊侠.大学数学课堂教学模式的进一步改革[J].大学数学,2010(增1):47-48.

[2]褚小婧,程向阳.大学数学研究性教学的实质及探索[J].大学数学,2011,27(1):16-20.

[3]梅建琴,邓玉萍.浅谈《 高等数学》中的研究型教学方法[J].课程教育研究,2013(4):125.

[4]黎虹,王中兴.应用型高等院校数学课程教学的思考[J].辽宁高职学报,2010,12(1):33-34.

[5]李灵晓,许丽萍.在高等数学习题课教学中开展研究性学习的实践[J].洛阳师范学院学报,2011,30(5):24-28.

[6]马书燮.数学教学改革的困境及对策[J].黑龙江高教研究,2011(6):177-179.

[7]张学润,王中东,徐向红.研究型教学在高等数学教学中的实施浅析[J].数学教育学报,2012(1):85-87.

[8]胡铁生,周晓清.高校微课建设的现状分析与发展对策研究[J].现代教育技术,2014,24(2):5-13.

Analysis on application of research-oriented teaching method

in higher mathematics course

LI Xiaomei

(School of Sciences, Zhejiang University of Science and Technology, Hangzhou 310023, China)

Abstract:Research-oriented teaching method has been widely adopted in many colleges and universities. But how to effectively use the mehtod is still worth exploring. Thus, the paper analyzes the application of research-oriented teaching method in higher mathematics course—an important basic course in the undergraduate program. It explores in details how to use research-based teaching according to the characteristics of higher mathematics with a wide scope of students, more content, less teaching hours and large-size class teaching. In the meantime, with the development of teaching reform under new social context and the features of research-oriented teaching method, it proposes some new models and approaches in research-oriented teaching method.

Key words:higher mathematics; teaching reform; research-oriented teaching; classroom teaching

中图分类号:G642.0;O13

文献标志码:A

文章编号:1671-8798(2015)01-0073-08

作者简介:李小梅(1956—),女,黑龙江省宝清人,副教授,主要从事高等数学的教学及研究。

基金项目:浙江省《基础数学》重点学科建设学术研究子项目(20141016)

收稿日期:2015-01-11

doi:10.3969/j.issn.1671-8798.2015.01.013