换热管固有频率计算方法

苏文献,　陈　功

(上海理工大学 能源与动力工程学院,上海　200093)



换热管固有频率计算方法

苏文献,陈功

(上海理工大学 能源与动力工程学院,上海200093)

换热器在石油、化工、医药、纺织、食品及冶金等领域应用十分广泛,在生产过程中换热器的性能对产品质量、能量利用效率以及整个生产系统运行的经济性和可靠性起着至关重要的作用.目前,虽然出现了很多新式换热器,如板壳式换热器、板框式换热器及双螺纹换热器等,但是,管壳式换热器由于结构简单、制造方便,能在高温和高压下使用,在工业应用中,管壳式换热器仍占据换热器使用的70%左右[1-2].

由于在工业生产中换热器振动破坏现象屡屡发生,这引起了人们对流体诱发振动的关注.1978年,在美国管式换热器制造商协会(TEMA)标准第6版中,首次将换热器管束振动列入标准,重点在于解决单相流体横向流诱发的振动,在之后的TEMA第7版,单独将流体诱导振动编入第6章.

在国内外科学研究工作的基础上,全国压力容器标准化技术委员会在组织编制钢制管壳式换热器标准GB 151-1989时,以参考件的形式将换热器管束振动列入附录.目前,在GB 151-1999附录E中列出的是经过修改和补充后的条目,它是根据国内管壳式换热器发展的需要并参照国际同类标准进行修改的.

由于流体诱发振动的复杂性,目前的技术水平难以对换热管束振动作详细解答,标准所提经验公式只是作为参考,并未对换热器设计作强制要求.本文分别按照GB 151-1999和TEMA所推荐的公式和有限元法对换热器管子的固有频率进行计算,比较其结果,并列出其他两种管壳式换热管的固有频率算法——Timoshenko法和Ganapathy法.

1管壳式换热器参数

某单程大型管壳式换热器采用固定管板式,有两块等间距弓形折流板,跨距为1 910 mm.因跨距较大,故未在折流板缺口处布置换热管,折流板缺口率为18%.换热器管子排列方式为等边三角形排列法,整台换热器共有5 513根管子,材料为304L不锈钢.换热器的结构尺寸如表1所示.

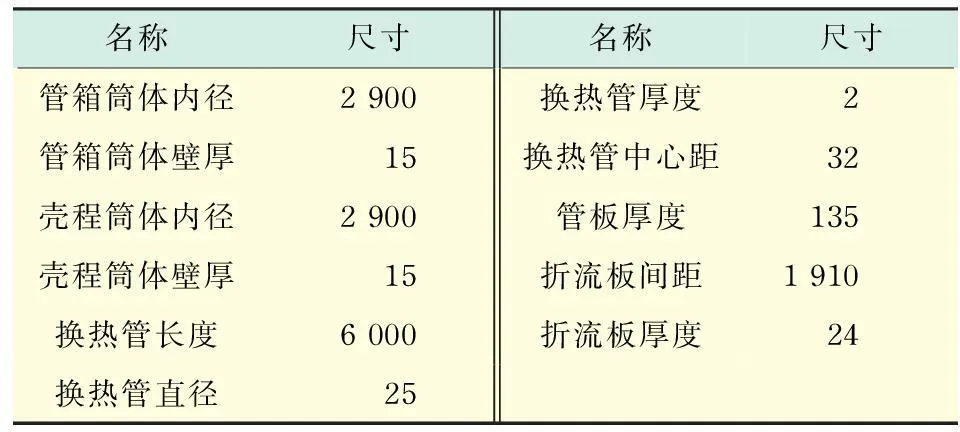
表1　换热器结构尺寸

2按照GB 151-1999计算换热管固有频率

GB 151-1999附录E对管壳式换热器管束的固有频率提出了详细的计算方法,对等跨距直管、非等跨距直管、有轴向力作用时的直管及U形管的固有频率都提出了计算公式[3].一般情况下,由于管板较厚,相对于管束振动,管板可以看作是刚性的,折流板与管子之间有很小的间隙,在管束与折流板的接触处,管子可以扭转、扰动,因此,在计算时换热管的支撑条件为:管子与管板接触端为固支,管子与折流板接触处为简支.

本换热器折流板等间距排列,如图1所示,在折流板缺口处没有布管,因此,所有管子固有频率及振型相同,按照以下公式进行计算:

(1)

(2)

(3)

(4)

(5)

式中:fn为管子固有频率;λn为频率常数,下标n为振型的阶数,查表2可知,λn一阶为12.648,二阶为18.469;E为管子的弹性模量;di为换热管内径;do为换热管外径;S为换热管中心距;l为跨距;m为单位换热管长的质量;mi为换热管内流体的质量;mo为被振动管排开的虚拟管外流体的质量;mt为空管质量;CM为附加质量系数,CM由S/do查图2,得CM=1.57;ρi为管内流体的密度;ρo为管外流体的密度.

图1　换热管支撑简图

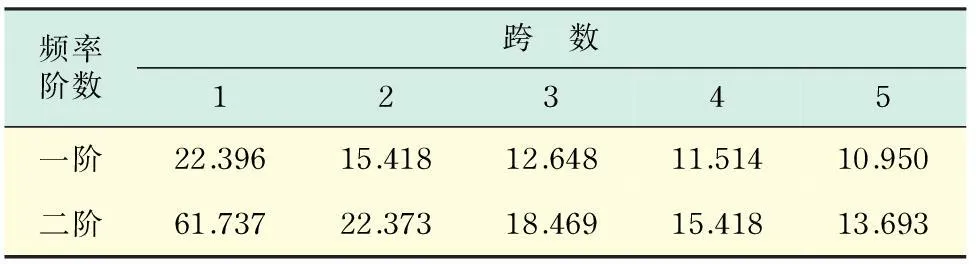
频率阶数跨 数12345一阶22.39615.41812.64811.51410.950二阶61.73722.37318.46915.41813.693

注：频率常数表摘自GB 151-1999附录E的表E2.

根据换热器结构及工艺参数可知,管子弹性模量E=1.97×105MPa,换热管内径di=21 mm,换热管外径do=25 mm,换热管中心距S=32 mm,换热器管束跨距l=1 910 mm,操作工况下管内气体密度ρi=0.112 2 kg/m3,管外冷却水密度ρo=994.877 kg/m3.将以上已知条件带入式(1)—(5)

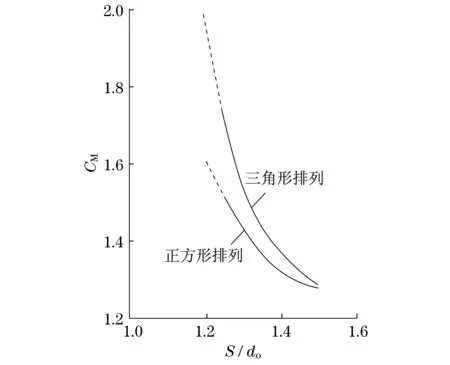
图2　附加质量系数

可求出换热管的前两阶固有频率

f1=17.395Hz

f2=25.401Hz

3按照TEMA标准计算换热管固有频率

TEMA标准是由美国管式交换器制造商协会所属的技术委员会编制的关于列管式换热器设计、制造和检验的标准,是目前世界上使用最广泛的列管式换热器标准.1978年颁布的TEMA标准第6版,首次将管束振动列入标准,在RGP-RCB-4.56这一节对管束振动进行了较为详细的介绍,对于计算等跨距换热管固有频率,标准推荐使用的公式与Macduff-Feglar得到的公式一致[4].1988年颁布的第7版,将流体诱导振动在第6章单独作了较为详细的介绍,在内容、范围和篇幅上,都较第6版有大的增加.最新2007年第9版的TEMA在振动这一章改动较少,在第6章TEMA使用范围中指出,由于振动问题的复杂性,TEMA对于振动只作为工程参考,不能保证换热器不发生振动破坏,同时,其他计算振动的方法仍然可以使用[5].早在1981年,董洁[6-7]就对TEMA标准第6版进行了实例讨论.TEMA对换热器固有频率求解作了简化,按照支撑情况不同,对于每段支撑管,分别计算其固有频率,然后选取最小值作为整个管子的基频,表达式为式(6),其中,参数单位为英制单位.

(6)

为了计算方便,在计算前将换热器直径、密度、跨度等已知条件的单位都换算为英制单位,统一代入式(6)进行求解,解得换热管基频

fn=13.609Hz

4按照Macduff-Feglar法计算换热管固有频率

在计算振动时,Macdaff-Felgar的方法被广泛应用[4],即TEMA第6版的RGP-RCB-4.562所推荐的公式,它的表达式为

(7)

式中：fn为管子固有频率;Cn为频率常数,下标n为振型的阶数,查表3可知，λn一阶为40.52,二阶为59.56;J为截面的惯性矩;g为重力加速度,取9.81 m/s2.

其余参数意义及单位与式(1)相同.代入换热器数据,可以求出换热器前两阶频率

f1=17.288Hz

f2=25.411Hz

表3　频率常数Cn

5按照其他公式计算换热管固有频率

目前计算换热管固有频率除了GB 151-1999和TEMA推荐的方法以外,还有Timoshenko法和Ganapathy法.

a. Timoshenko法.

(8)

式中,λ为特性系数,1/m;

b. Ganapathy法.

(9)

6有限元法计算换热管固有频率

有限元方法起始于20世纪40年代,经过70多年的发展,已经在航天、汽车、机械及化工等领域广泛应用.它的基本概念是用较为简单的问题代替复杂问题,然后进行求解,其应用范围包含固体力学、流体力学、传热学、电磁学、声学及生物力学等.由于采用有限元方法可以很方便地求解复杂结构振型,该方法已经在机械、化工中得到了广泛的应用[8-10].

6.1单元选择

为了简化模型,换热器管子采用BEAM188梁单元,该单元几何结构如图3所示.K,J为自由度.BEAM188适合用于分析细长及中等厚度粗短梁结构.该单元基于Timoshenko梁理论,考虑结构受到的剪切变形影响.BEAM188单元为3D二次梁单元,在默认情况下,每个节点有6个自由度,包括X,Y,Z这3个方向平移和绕X,Y,Z这3个方向旋转.当设置ANSYS中的参数KEYOPT(1)=1时,会增加第7个自由度的翘曲幅度自由度.该单元适合在线性、大旋转或者非线性大应变情况下使用.

图3　BEAM188单元几何结构示意图

6.2模型介绍

建立仅含单根换热管模型,该模型与前文标准及其他经验公式所采用的模型完全一致,可以验证经验公式与有限元计算结果的一致性.

该换热器的换热管及管板、折流板的材料均为304L不锈钢,管板、折流板密度采用材料实际密度进行计算,由于本文不直接考虑流体的流动对换热管振动的影响,而参照GB 151-1999热交换器中运用等效密度法更加简单、间接地考虑外部流体对换热管振动的影响,因此,换热管的计算密度采用等效平均密度进行计算,计算式如式(2)—(5)所示.材料属性如表4所示.

表4　材料属性表

6.3换热管模态分析

6.3.1单管模态分析

对于单根换热管模态分析,这里选择简化模型,模型及约束与文中经验公式所采用的模型完全一致,换热管与管板处为固支,折流板与换热管接触处为简支;换热管与管板的连接处可以看作是固支.换热管和折流板处有很小缝隙,折流板主要起支撑作用,此处换热管不会发生径向位移,但是,会转动及轴向移动,故此处可以看成是简支,约束X,Y这2个方向的自由度.具体有限元模型如图4所示.

图4　单根换热管有限元模型

在ANSYS通用后处理中提取前两阶频率,结果如图5和图6所示.Xmax,Xmin分别为X方向的最大变形和最小变形.

图5一阶振型f1=17.419 Hz

Fig.5First modef1=17.419 Hz

图6二阶振型f2=25.453 Hz

Fig6Second modef2=25.453 Hz

6.3.2单管含管板模态分析

如图7所示,采用SOLID186单元建立管板和换热管的模型,折流板和换热管之间耦合X,Y方向的自由度.采用模态分析技术,在ANSYS后处理模块中提取前两阶模态频率,前两阶振型如图8—10所示.XW,YW,ZW分别为工作平面的坐标.从图9中可以发现,折流板的一阶固有频率介于换热管的前两阶固有频率之间.

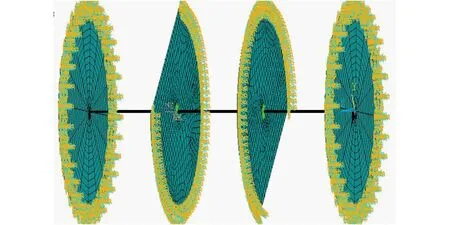
图7　单管的有限元模型

图8　换热管的一阶振型f1=17.369 Hz

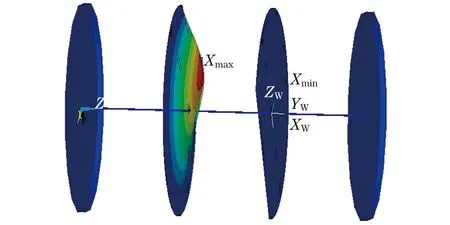
图9　折流板的一阶振型f1=21.748 Hz

图10　换热管的二阶振型f2=25.320 Hz

7结果分析

对采用有限元法、GB 151-1999、TEMA及Macdaff-Fegla法计算得到的换热管固有频率进行比较,结果如图11所示.

图11　各种方法比较

通过图5—11可以看出:

a. 有限元法计算的单管模型以及包含折流板的单管模型的换热管一阶频率、GB 151-1999计算的换热管一阶频率、Macdaff-Felgar所得的换热管一阶频率分别为17.419,17.369,17.395,17.288 Hz,二阶频率分别为25.453,25.320,25.401,25.411 Hz,4种方法计算的结果非常接近.根据文献[11]第3章中试验所得,在管束中如果只有1根管子振动而其他各管固定,则此时测量得到的固有频率与Macdaff-Felgar计算的值相当符合,故在工程实践中计算单管的固有频率时可以采用有限元法简化计算.

b. 在计算包含折流板结构的换热管模型时,折流板的一阶频率在管子的一阶频率和二阶频率之间,故在工程实践中分析换热管的振动破坏时,应当考虑到折流板的横向振动会加速换热管的磨蚀和破坏.

c. TEMA标准采用分段计算各段的频率,并且取最小值作为结构的固有频率,而GB 151-1999以及有限元法均考虑了多跨度对结构的影响,故通过TEMA计算得出的固有频率要小于GB 151-1999以及有限元法计算得到的固有频率.

参考文献：

[1]钱颂文.换热器设计手册[M].北京:化学工业出版社,2002.

[2]刘海刚.大型管壳式换热器管束动力特性分析及流体诱导振动研究[D].上海:上海理工大学,2012.

[3]全国压力容器标准化技术委员会.GB151-1999.管壳式换热器[S].北京:中国标准出版社,2000.

[4]聂清德,连华英,侯增英.多跨管固有频率的计算[J].压力容器,1984(4):51-55.

[5]聂清德,谭蔚,吴皓.多跨U形管固有频率的计算[J].压力容器,2011(9):15-21.

[6]董洁.TEMA管式换热器标准计算实例(一)(1978年第6版)[J].化工设备与管道,1981(6):25-41.

[7]董洁.TEMA管式换热器标准计算实例(二)[J].化工设备与管道,1982(1):42-64.

[8]苏文献,许伍.基于ANSYS压力容器不等厚过渡区的强度优化[J].上海理工大学学报,2014,36(1):81-85.

[9]苏文献,金玉龙,韩超.单塔风诱导振动破坏分析[J].上海理工大学学报,2013,35(4):391-396.

[10]杜宝江,丁鹏鹏,于亚君,等.基于有限元分析的机油泵卡死现象设计改进[J].上海理工大学学报,2015,37(3):269-273.

[11]程林.换热器内流体诱发振动[M].北京:科学技术出版社,1995.

(编辑:石瑛)

第一作者： 李海军(1987-),男,硕士研究生.研究方向:微流体机械内部流动.E-mail:lihaijun1113@126.com

第一作者： 管屏(1958-),男,讲师.研究方向:热工能源、电子电气设备热分析、智能优化研究.E-mail:guanping@sspu.edu.cn

摘要：采用有限元分析软件ANSYS计算某管壳式换热器的换热管的固有频率,将其计算结果与采用相关标准(GB 151-1999和TEMA)和经验公式(Macdaff-Felga法)计算得到的固有频率结果进行分析比较.结果表明,采用有限元法计算得到的固有频率与采用GB 151-1999标准以及Macdaff-Felga法的计算结果保持一致,采用TEMA标准计算的固有频率结果小于采用其他几种方法计算的结果.另外,有限元法的计算结果显示,折流板的一阶频率在管子的一阶频率和二阶频率之间.

关键词：管壳式换热器;固有频率;经验公式;有限元法

Method of Computing Natural Frequencies of TubeSU Wenxian,CHEN Gong

(School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract：Finite element software ANSYS was used to calculate the natural frequency of tube in a shell and tube heat exchanger.The calculation result was compared with the analytical results by using the related standards (GB 151-1999 and TEMA) and empirical formula (Macdaff-Felga).The natural frequency of tube calculated by the finite element method is consistent with those calculated by GB 151-1999 and Macdaff-Felga,and the frequency calculated by TEMA is smaller compared with those calculated by other methods.The finite element computation also shows that the first mode of baffle lies between the first mode and the second mode of tube.

Key words：shell and tube heat exchanger; natural frequencies; empirical formula; finite element method

通信作者：王企鲲(1978-),男,副教授.研究方向:低雷诺数粘性流体力学.E-mail:wangqk@usst.edu.cn 单彦广(1974-),男,教授.研究方向:两相流动与传热.E-mail:shan@usst.edu.cn

基金项目：教育部博士点基金资助项目(2011320120003) 上海市教委科研创新基金重点资助项目(13ZZ119)

收稿日期：2014-08-14 2014-10-09

DOI：10.13255/j.cnki.jusst.2015.06.007 10.13255/j.cnki.jusst.2015.06.006

文章编号：1007-6735(2015)06-0546-05 1007-6735(2015)06-0540-06

中图分类号：TQ 051

文献标志码：A