基于遗传算法的单点交叉口信号配时优化

慕飞飞,　张惠珍

(上海理工大学 管理学院,上海　200093)



基于遗传算法的单点交叉口信号配时优化

慕飞飞,张惠珍

(上海理工大学 管理学院,上海200093)

随着社会的发展和人们生活水平的提高,中国的城市化进程持续推进,机动车数量与日俱增,给人们带来出行便利的同时也导致了许多交通问题,特别是交通拥堵严重困扰着人们的日常生活.交叉口是城市交通的瓶颈,其交通问题尤为严重[1].然而,受城市土地的限制,扩建道路面临着极大困难.因此,对交叉口信号控制进行研究,是解决交通拥堵问题的有效途径之一.虽然,国内外很多学者已经开始对线控、面控进行研究,但缺乏实际应用,单点交叉口交通信号控制系统依然在城市交叉口控制中广泛使用[2-3].因此,解决交通问题的主要出发点依然是单个交叉口.另外,虽然对实时信号控制的研究开始得比较早,但是,目前很多道路信号配时还是根据简单的Webster算法计算得到,计算结果不够精确.相比较,智能优化算法具有一定的先进性,大量学者将各种优化算法应用到智能交通研究领域中,在理论研究方面取得了较多的成果.

20世纪70年代,英国学者Webster提出了ARRB,TRRL等优化方法[4].此外还有一种应用比较广泛的YD模型,它考虑的信号配时指标除了车辆的延误外,还将信号周期、相位关键车流量、停车率及排队长度考虑在内.除了建模方法上的创新,国外还开发了很多信号配时软件系统,如TRANSYT,Cabal[5],Synchro,SCOOT[6],MOTION以及SCAT等.

自2000年以来,国内学者对交叉口信号配时方面的研究也获得了很多成果.孙超等[7]分析了Synchro仿真系统中的信号配时优化模型,并以广州市天河北路与天河东路交叉口为例对优化模型进行了验证和分析.田丰等[8]针对单交叉口多相位交通流建立了动态信号配时模型,以交叉口车辆平均延误最小为控制目标并运用自适应遗传算法对信号配时问题进行了优化.程方[9]通过对城市交叉口交通流微观仿真模型的分析,针对给定城市交叉口各路口的一些几何参数和交通量,运用VISSIM进行交通系统的建模和仿真,得到了最佳配时方案,并最终减少了路口的交通延误.陈利红等[10]将VISSIM仿真软件与信号配时相结合而形成的信号交叉口优化方法,对交叉口进行了实例分析.朱晓宁等[11]建立了针对交叉口配时优化的双层规划模型.

通过比较这些方法的可操作性及优缺点,本文选取平均停车次数、交叉口平均延误为效益评价指标,采用实数编码的遗传算法对单点交叉口信号配时进行优化,最后,以上海某一交叉口为例进行了优化和分析,证明了该方法的实用性.

1建立目标函数

交通效益的评价指标主要有:饱和度或道路的通行能力(实际到达交通量与通行能力之比)、停车次数、停车率、油耗、行程时间、延误等.通常来说,对道路进行交通信号控制的目的是要使交通网络或单个交叉口获得较好的交通效益[12].传统的干道协调控制设计的目标是获取最大绿波宽度,针对现今社会大多数城市交叉口经常出现交通拥堵的情况,可以采取减少车辆通过协调控制范围内各交叉口的总停车次数或总延误时间[13]来改善交通拥堵问题.

综上考虑,目标函数包含两部分:一部分为交叉口车辆的平均延误;另一部分为交叉口的平均停车次数.

1.1平均延误

车辆的延误时间是指车辆在受阻情况下通过交叉口所需时间与正常行驶同样距离所需时间之差.在一个信号周期内,对于某一相位的进口道来说,到来的车辆受到的延误为周期车辆延误,若一个路口包含了几个信号相位,那么总延误时间D可以表示为

(1)

在一个周期内交叉口各相位延误的加权平均值是车辆平均延误时间,即

(2)

其中,根据Webster定时信号交叉口延误公式,第i相位每辆车的平均延误时间为

式(3)中,第一项为平均一致性延误时间,它是由于红、绿信号灯交替变化而引起的额外延误,但交通流均匀到达;第二项为平均随机延误时间,它是由交通流饱和度大于1时出现超载现象及交通流到达的随机性引起的延误.

1.2平均停车次数

(4)

一个周期内交叉口的车辆平均停车次数为

(5)

1.3目标函数

根据实际到达交通量,建立交叉口动态信号控制优化模型,以控制周期内平均停车次数和交叉口车辆的平均延误作为目标函数,以信号周期内的绿灯时间及周期时长为优化参数.通过运用Webster算法及遗传算法确定控制周期内各相位的最优绿灯时间及周期时长,并对结果进行比较,从而使总延误及总停车次数目标函数值最小,达到优化的目的.

通过将停车次数和延误作为目标函数,从而寻找目标函数的最小值[14].目标函数为

约束条件为

(7)

(8)

(9)

2最佳优化配时算法

2.1Webster算法

Webster算法是计算信号配时的一种方法,在目前交通信号控制领域中比较常见.它最主要的思想是计算车辆延误和最佳的周期时长,目标函数为最小的车辆延误时间,在进行周期时长计算时,也是以车辆延误为基础的.

通过用近似解法,可以得到定时信号最佳周期时长[15]为

(10)

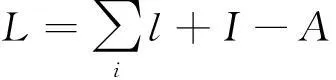
(11)

2.2遗传算法

2.2.1实数编码遗传算法

遗传算法(genetic algorithm,GA)是一种比较先进的参数寻优算法,通过运用仿生原理从而实现在解空间的快速搜索.遗传算法对于不易建立数学模型的场合,其实用价值较为突出,现在广泛应用于解决大规模组合优化问题,所以适用于交通系统.

传统的遗传算法具有很多的优点,比如可扩充性较强,思想简单,可操作性好,鲁棒性好,而且在对路网进行协调控制时,不会出现“维数灾难”的问题.但是,传统的二进制编码遗传算法在求解连续函数时需编码和解码,会影响运行速度和精度,特别在搜索大空间范围时更明显.而实数编码的编码长度通常为变量个数,而且适合于表示范围很大的数,便于较大空间的搜索,从而可以避免以上所涉及的问题,并能改善遗传算法的计算复杂性.同时,实数编码能够有效避免二进制编码中所遇到的hamming悬崖问题.

2.2.2算法迭代步骤

a. 基本参数的设定:比如最大遗传代数、种群大小、交叉概率、个体长度等.

b. 编码:GA通过使用解空间里面的解数据来表示遗传空间里的基因型串结构数据,然后再对数据进行搜索.本文编码长度为变量个数,对所研究的问题进行编码,编码采用实数编码.

c. 初始种群生成过程:随机情况下产生M个串结构数据的初值,各个数据都是一个个体,这样,由上述的M个个体便形成了一个种群.本文通过随机产生预定种群数目的初始群体,将这些串结构数据作为初始点开始进化.

d. 适应度的计算:目标函数为f(x),目标函数通过给每一个个体非负的价值数,从而实现转换目标函数的函数值.同时,由于目标函数求解的是最小值,因此可以通过动态函数惩罚法来构造适应度函数,所构造的适应度函数为

(12)

式中,ε为任意常数,ε>0,从而确保适应度函数F(x)为正数.

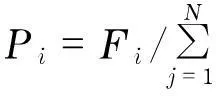
f. 交叉:采用实数交叉法,第l个染色体al和第k个染色体ak在j位的交叉操作方法为

(13)

式中,b是[0,1]区间的随机数.

g. 变异:采用非均匀变异.第i个个体的第j个基因aij进行变异的操作方法为

(14)

式中:amax是基因aij的上界;amin是基因aij的下界;f(g)=r2(1-g/Gmax)2,r2是随机数,g是当前迭代次数,Gmax是最大进化次数,r为[0,1]区间的随机数.

3实例分析

选取上海崧泽大道明珠路十字交叉口,其中明珠路为南北走向,崧泽大道为东西走向.该交叉口为四相位控制,其相位控制方案如图1所示,交叉口内部渠化图如图2所示,交叉口现状数据如表1所示.

图1　相位图

为了充分证明算法及模型的有效性,首先应用传统的Webster优化算法进行计算,其中每相位启动损失时间为2 s,绿灯间隔时间为7 s,黄灯时间为2 s.在计算得出最佳周期及各相位有效绿灯时长后,再进一步计算出平均延误及平均停车次数,最终结果如表2所示(见下页).

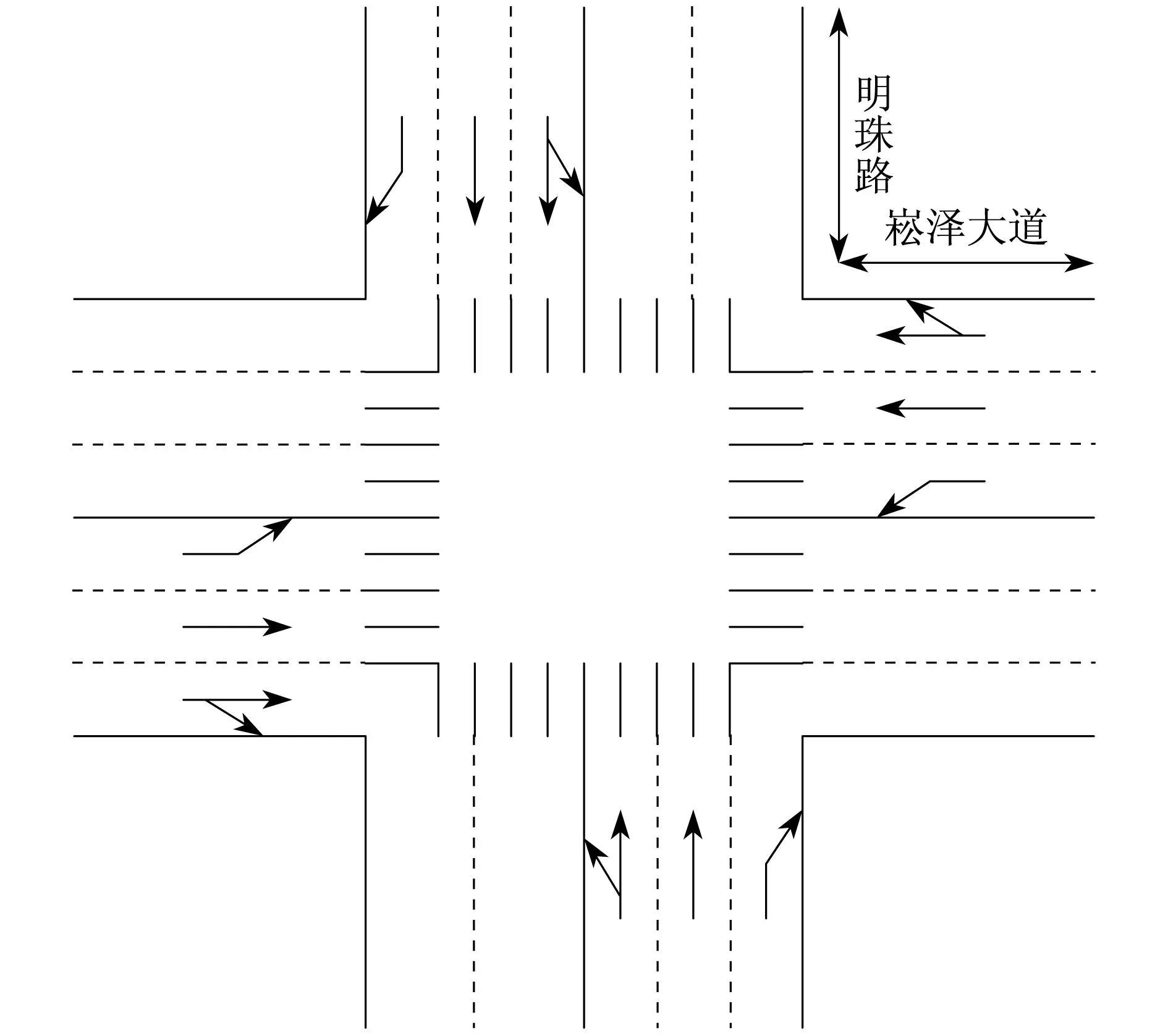
图2　交叉口渠化图

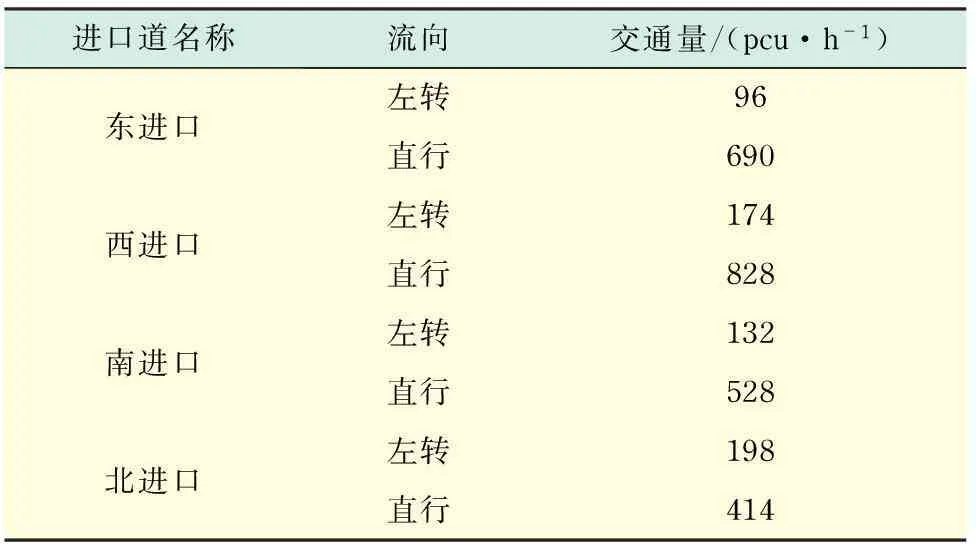
进口道名称流向交通量/(pcu·h-1)东进口左转96直行690西进口左转174直行828南进口左转132直行528北进口左转198直行414

应用Matlab语言进行编程,最小信号周期为40 s,最大信号周期为120 s;第一、三相位最小绿灯时间为20 s,最大绿灯时间为80 s;第二、四相位最小绿灯时间为10 s,最大绿灯时间为40 s.程序中必要的一些参数分别设置为:种群大小为50,最大遗传代数为500,染色体长度为4,交叉概率为0.8,变异概率为0.01.在500次运行优化过程中,第269代开始收敛于最优解,运行结果如表2所示.

从表中可以看出:应用了遗传算法进行优化之后,周期变为118 s,比现状缩短了19%;平均延误变为36 s/veh,比现状下降了20%;平均停车次数变为0.736 1,比现状下降了11%.同时还可以看到,遗传算法所有的优化指标均优于Webster算法的优化指标.

由此可见,遗传算法得出的优化方案优于现有控制方案及经典的Webster算法得出的方案,在很大程度上提高了交叉口的服务水平.

表2　两种优化算法优化结果与现状对比

4结束语

研究了单点交叉口的信号配时优化问题,通过建立一个效益评价目标函数,以相位绿灯时间、周期时长作为约束条件,并使用实数编码遗传算法进行编程,应用Matlab软件进行仿真优化,最后得出了优于现状及传统Webster算法的信号参数,提高了交通效益，从而证明了优化模型及遗传算法的有效性.下一步将会对多相位十字交叉口在有非机动车和行人影响情况下的配时方案作进一步研究,使配时模型可以应用于更多的实际交通控制中；也将进一步研究交叉口的线控、面控,并将使用更多先进的智能算法进行优化.

参考文献：

[1]顾静航.城市轨道交通枢纽一体化布局及换乘研究[D].上海:同济大学,2008.

[2]曾松林.城市单交叉路口交通信号的控制方法研究[D].成都:西南交通大学,2013.

[3]柴干,赵倩,蒋珉.城市智能交通信号控制系统的设计与开发[J].浙江大学学报:工学版,2010,44(7):1241-1246.

[4]李群祖,夏清国,巴明春,等.城市交通信号控制系统现状与发展[J].科学技术与工程,2009,9(24):7436-7442.

[5]程婉燕.基于多智能体的城市交通信号控制的协调与优化[D].福州:福建农林大学,2009:23-35.

[6]钱海峰.基于短时交通流预测的交通控制算法研究[D].北京:北京工业大学,2009:37-45.

[7]孙超,徐建闽.城市单点交叉口的信号配时优化研究[J].交通与计算机,2008,26(6):6-10.

[8]田丰,边婷婷.基于自适应遗传算法的交通信号配时优化[J].计算机仿真,2010,27(6):305-308.

[9]程方.基于VISSIM的单点交叉口微观模型仿真[J].软件,2011,32(9):49-50.

[10]陈利红,邓璇.应用VISSIM仿真进行信号交叉口配时优化[J].河北交通职业技术学院学报,2013,10(4):54-57.

[11]朱晓宁,隆冰.多路公交优先交叉口配时优化的双层规划模型[J].交通运输工程学报,2014,14(1):103-111.

[12]姚佼,杨晓光.车路协同环境下城市交通控制研究[J].上海理工大学学报,2013,35(4):397-403.

[13]常云涛,彭国雄.基于遗传算法的城市干道协调控制[J].交通运输工程学报,2003,6(2):106-112.

[14]玄光男,程润伟.遗传算法与工程优化[M].北京:清华大学出版社,2004.

[15]宋晓鹏,韩印,姚佼.基于NSGA算法的公交车辆调度优化模型[J].上海理工大学学报,2014,36(4):357-361.

(编辑:丁红艺)

上海理工大学学报

2015年第37卷第1～6期

摘要：以相位的周期时长、绿灯时间作为约束条件,平均停车次数、平均延误最小作为优化目标函数,建立了信号配时优化非线性模型.以上海某一交叉口作为研究对象,将其交叉口的交通数据应用于该模型中,以Matlab为模拟环境,应用实数编码遗传算法对其求解.运行结果显示:交叉口的信号周期由145 s变为118 s,缩短了19%;车辆的平均延误由45 s/veh变为36 s/veh,下降了20%;车辆的平均停车次数由0.828 2变为0.736 1,下降了11%.研究结论表明,该方法得出的信号配时方案可以有效地减少停车延误和停车次数,优于现有控制方案及传统的Webster算法得出的方案,从而证明了此模型的实用性.

关键词：交通控制; 单点交叉口; 遗传算法; 平均延误

Signal Timing Optimization at Single-Point Intersection Based on Genetic AlgorithmMU Feifei,ZHANG Huizhen

(Business School,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract：A non-linear model for signal timing optimization was created to study the problem of four phases signal timing optimization at city’s single-point intersections.The minima of average delay and average stop times were regarded as the optimization objective function,the phase green time and the cycle time were regarded as the constraints and one of the Shanghai intersections was regarded as the research object.With the real-coded genetic algorithm in the Matlab simulation environment,the optimization problem was solved.By applying the method,the intersection cycle time changes from 145 s to 118 s,shortened by 19%,the average vehicle delay changes from 45 s/veh to 36 s/veh,shortened by 20%,and the average stops changes from 0.828 2 to 0.736 1,shortened by 11%.The results show that the signal timing plans drawn by using this method can reduce parking delay and stops effectively,thus it proves the usefulness of the model which is better than the existing control scheme and the Webster optimization algorithm.

Key words：traffic control; single-point intersection; genetic algorithm; average delay

中图分类号：U 491.51

文献标志码：A