Wenger图的控制数

刘　凌

(上海理工大学 理学院,上海　200093)



Wenger图的控制数

刘凌

(上海理工大学 理学院,上海200093)

1问题的提出

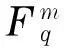
这些结论对于研究极值图论中偶圈的Turán数的精确阶都有十分重要的意义[4-6].在文献[7]中,Viglione确定了Hm(q)的直径(图中任意两点间距离的最大值).受此启发,本文将研究Hm(q)的另一个结构参数——控制数.

首先给出Wenger图Hm(q)和控制数的定义.

定义2[8-10]设G=(V,E)为一个图,D⊆V,若对每一个v∈VD,存在u∈D,使uv∈E,则称D为图G的一个控制集,G的控制数

定义3设G=(X∪Y,E)为一个二部图,M⊆X,若对于每个v∈Y,存在u∈M,使uv∈E,则称M为Y在X中的一个控制集,Y在X中的控制数

同样,可定义X在Y中的控制数

易见,二部图G的控制数

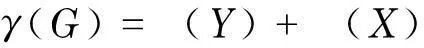
设v是图G中的一个点,G中与点v相关联的边的条数称为点v的度,用d(v)表示.下面的命题1在文献[1]中已有证明,为了文章的完整性,这里给出了它的另一种证明.

命题1在Hm(q)中,对任意的A∈X,B∈Y,都有A与B的度相等,都为q.

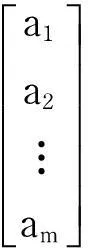
证明由Hm(q)图中AB相邻的定义,可知A的度必为q,又对任意B=[b1,b2,…,bm]T∈Y,若A=[a1,a2,…,am]T∈X，A与B相连,则a1,a2,…,am为方程组

(1)

的解,其系数矩阵

的秩为m-1,从而方程组(1)的解空间维数为1,故X中恰有q个点与B相连,B的度也为q.

2Wenger图Hm(q)的控制数

通过构造Hm(q)的一个控制集,并证明其是点数最小的控制集,从而确定Hm(q)的控制数.

引理1设a∈Fq,Hm(q)=(X∪Y,E),

则M中任意两个不同的点都没有公共邻点.

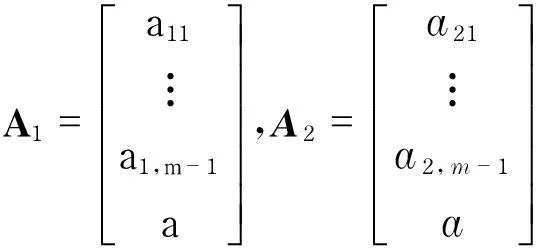
故有

从而a1,m-1-a2,m-1=0,a1,m-2-a2,m-2=0,…,依此类推,a11-a21=0,故a1j=a2j,j=1,2…,m-1,即A1=A2,矛盾.

命题2设a∈Fq,则M={[a1,…am-1,a]T|a1,…,am-1∈Fq}⊆X为Hm(q)中Y在X中的控制集,并且Y在X中的控制数为qm-1.

证明由命题1,X中每一个点的度为q,M中共有qm-1个点,每个点的度均为q.又由下面的引理2可知,M中不同的A点一定与Y中不同的B点相连,从而Y中所有qm个点与M中点相连且没有重复,M为Y在X中的控制集,并且是含有点数最少的控制集,从而Y在X中的控制数为qm-1.

引理2设b∈Fq,则N={[b1,…bm-1,b]T|b1,…,bm-1∈Fq}⊆Y,则N中任意两个不同的点都没有公共邻点.

证明在N中任取两个不同的点

b1j=b2j，j=1,2…,m-1,即B1=B2,矛盾.

与命题2同理得命题3.

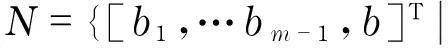
命题4γ(Hm(q))=2qm-1.

证明由二部图的G=(X∪Y,E)的控制数γ(G)=ξ(Y)+η(X)可知,Wenger图Hm(q)的控制数为Y在X中的控制数qm-1与X在Y中的控制数qm-1之和.

参考文献：

[1]Wenger R.Extremal graphs with noC4,C6orC10’s.[J].Journal of Combinational Theory Series B,1991,52(1):113-116.

[2]Shao J Y,He C X,Shan H Y.The existence of even cycles with specific lengths in wenger’s graph[J].Acta Mathematicae Applicatae Sinica,English Series,2008,24(2):281-288.

[3]Lazebnik F,Thomason A,Wang Y.On some cycles in Wenger Graphs[EB/OL].[2014-12-25].http://www.math.udel.edu/~lazebnik/papers/LazebnikTho-masonWang2014 Submitted.pdf.

[4]周敏,何常香.单圈图依次小Q-特征值排序[J].上海理工大学学报,2013,35(1):21-26.

[5]徐丽珍,何常香.双圈图的无符号拉普拉斯特征多项式的系数[J].上海理工大学学报,2014,36(1):12-14.

[6]沈富强,吴宝丰.最小Q-特征值为给定整数的一类图[J].上海理工大学学报,2014,36(5):425-428.

[7]Viglione R.On the diameter of wenger graphs[J].Acta Applicandae Mathematica,2008,104(2):173-176.

[8]Bondy J A,Murty U S R.Graph theory and its applications[M].New York:MacMillan Press,1976.

[9]张先迪,李正良.图论及其应用[M].北京:高等教育出版社,2005.

[10]彭茂.图的控制集的一些相关问题的研究[D].上海:上海交通大学,2008.

(编辑:石瑛)

第一作者： 马杰(1975-),男,副教授.研究方向:功能纳米材料的构筑与应用.E-mail:majie@usst.edu.cn

摘要：Wenger图Hspan(q)是定义在有限域Fspan上的q-正则二部图.根据二部图G=(X∪Y,E)的控制数为Y在X中的控制数与X在Y中的控制数之和,采用矩阵运算的方法在Hspan(q)中通过构造含点数最少的控制集,说明了这两个控制数应该相等,从而确定了Wenger图的控制数.

关键词：二部图; Wenger图; 控制集; 控制数

Domination Number of Wenger GraphLIU Ling

(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract：Wenger’s graph Hspan(q) is a q-regular bipartite graph in the field Fspan.Considering that the domination number of a bipartite graph G=(X∪Y,E) is the sum of Y’s domination number in X and X’s domination number in Y,by using the matrix operation,the domination set of Hspan(q) with minimum cardinality was constructed.It is proved that the two domination numbers are equal,and then the domination number of Hspan(q) was determined.

Key words：bipartite graph; Wenger graph; domination set; domination number

基金项目：上海市自然科学基金资助项目(15ZR1428500)

收稿日期：2014-09-18

DOI：10.13255/j.cnki.jusst.2015.06.003

文章编号：1007-6735(2015)06-0520-07

中图分类号：O 157.5

文献标志码：A