动态网络中行业因素与股市波动性研究

周明华，俞　伟，陆　川

(浙江工业大学 理学院，浙江 杭州 310023)

动态网络中行业因素与股市波动性研究

周明华，俞伟，陆川

(浙江工业大学 理学院，浙江 杭州 310023)

摘要：股票市场的波动性一直是金融领域的一个研究重点，行业因素对股市波动性的影响也是投资者关注的一个焦点.从复杂网络视角出发，以行业内股票相关性强弱(RIL)为指标实证研究了行业因素与股票波动性之间的联系.研究发现不同行业的RIL指标有不同的参考标准，于是对原有的RIL指标进行了改进得到新指标RIL*.在以沪深300样本股为例的实证研究中发现采矿业、金融业和房地产业内的股票受行业因素影响最强.研究还发现股票网络结构变化和股市波动性之间存在联系，当行业因素影响急剧降低时，行业内的股票走势会猛烈上升或下降.

关键词：动态网络；波动性；行业因素；沪深300

The study on the relationship between industry factor and stock

market volatility in dynamic networks

ZHOU Minghua, YU Wei, LU Chuan

(College of Science, Zhejiang University of Technology, Hangzhou 310023, China)

Abstract:Stock market volatility has been one of the most important aspects in studying financial market. Investors pay attention to the impact of industry factor when making an investment decision. We empirically investigate the relationship between the industry factor and the stock market volatility from the perspective of complex networks through Relative Industry Link (RIL) measure. In our study, we find that there are different standards in different industries so that the original RIL index is improved to get a new index RIL*. With the empirical study on cases of Hushen300 stocks, we find that stocks in the fields of mining industry, financial industry and real estate industry are affected mostly by industry factors. The study also shows that there is some relationship between the network structure and stock market volatility. When industry factors drastically fall, stock movements within the industry will rise or fall violently.

Keywords:dynamic network；volatility；industry factor；Hushen300

波动性是股票市场的一个重要特征，没有波动性股票市场将失去投资价值和存在的意义.近20年来，许多学者提出了各种数学模型来研究股票的波动性，如GARCH模型[1]，SV模型[2]，隐含波动率模型[3]，遗传算法[4]等.在研究过程中发现了许多关于股票市场波动存在的特性，如尖峰后尾特性、波动聚集性、波动长记忆性[5]等特征.行业因素是投资者投资时对股票选择的一个重要考虑因素.关于行业因素的研究也有很多[6-8].这些研究中分别采用了GARCH模型、dummy variable model和方差分量模型来研究.自从1999年，Mantegna用最小生成树方法(MST)构造股票网络以来[9]，越来越多的学者用网络演化方法来研究股票市场.关于股市波动性研究方面，Chi等通过股票网络构造了一个“度指数”来研究大盘走势[10]；Wiliński等通过MST方法发现当股市发生动荡时，股票网络将从无标度结构变成星形树结构[11].事实上，复杂网络方法也可以用来研究行业因素与股市波动之间的关系.

从网络演化角度入手，研究行业因素与股市波动性之间的关系已经有人跨出了第一步.tefan Lyócsa构造了RIL指标描述行业因素的强弱[12]，但在其研究中，只能给出数值模拟结果，该方法未得到完善.事实上，随着研究的深入可以发现不同行业的RIL指标有不同的参考标准(标准值)，因而它不能直接用来作为衡量行业因素强弱的标准.针对这一缺陷进行改进，得到新指标RIL*.在实证分析中，对比原始RIL指标说明了改进后的RIL*能排除不同行业衡量标准不同的干扰.在关于股票波动性研究中发现对于整个研究期内RIL*均值高的行业，当RIL*值剧烈下降时，该行业的整体走势将发生剧烈变化，或猛烈上升或猛烈下降.

1股票网络构建

自从Mantegna将MST方法应用到股票网络构建后，MST方法已经成为一种用来构造股票网络的常用方法.它不但可以过滤出股票网络中的重要信息，还可以用来解释网络拓扑结构和股票分类之间的内在联系[1].行业分类作为股票分类的一种，利用MST方法研究行业因素对股票市场的影响也是十分合适的.

构建MST的方法有很多，常用的有prim算法Kruskal.文[13]中说明了如何选取合适的最小生成树分析复杂网络，并在结论中指出Kruskal算法不适合用于构造MST分析复杂网络.prim算法虽非最优方法，但其方法简单且符合文[13]中的要求，故选用prim算法构造MST.

使用MST方法构造股票网络时，将每一支股票当作网络中的一个点，股票与股票之间的关系强弱作为边权.在大多数情况下，股票与股票之间的关系用其对数收益率的皮尔逊相关系数衡量.

在计算皮尔逊相关系数前，首先要得到每一支股票的对数收益率.第i支股票在T时刻的对数收益率ri,T[14]可表示为

ri,T+1=lnPi,T+1-lnPi,T

(1)

式中Pi,T表示第i支股票在T时刻的收盘价.

股票i和j皮尔逊相关系数表达式为

(2)

式中〈…〉表示变量在一段连续时间内的均值.

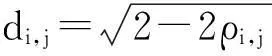
任意两支股票之间，都可以用上述方法得到它们之间边的权重.这样就可以得到一张关于股票市场的完全图.然后用prim算法可以得到这张完全图的一个最小生成树(MST)[9]，这个MST就是股票市场的网络图.

研究一段较长时间内，股票网络上行业因素随时间的演化特性时需要对每一个股票交易日都用上述方法得到一张该时刻的股票网络图.随后，通过研究网络演化来研究行业内股票相关性的变化，以此分析行业因素与股票市场波动性之间的关系.

2RIL指标及其性质

行业因素指标RIL是用来描述一个行业内股票相关性的强弱的指标，值越高说明行业内股票相关性越强，因此其行业因素也越强.在理论推导了不同行业的RIL标准值后，对于引言中提到RIL指标的不足之处进行了改进.改进后得到的新指标RIL*将作为后面实证分析行业因素与股市波动性之间关系的主要工具.

2.1行业内股票相关性(RIL)

T时刻行业l内股票相关性水平(RILl,T)定义[12]为

(3)

由定义1可知：0≤RILl,T≤1，当RILl,T值接近0时，说明该行业l内各股票之间相关性很低，该行业内股票不存在行业因素的影响；当RILl,T值接近1时，说明该行业l内股票之间紧密相关，行业因素对该行业内股票影响很强.

2.2各行业RIL的标准值

RIL指标需要一个具体的标准来划分行业因素的强弱.当RIL值高于这个标准值时，才能称该行业内股票具有相关性.这个特定的值称为标准值.

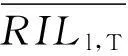
(4)

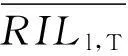
2.3RIL的改进

由于不同行业RIL指标的标准值不同，不能直接用RIL指标来衡量不同行业行业因素影响的强弱，需要对其进行该进.在改进中需要注意到RIL指标有两个特点：对于任意行业l，当RIL=0时，表示该行业内股票在网络中所代表的点都没有直接相连的边；当RIL=1时，该行业内的股票在网络中所代表的点构成子树.在改进过程中，需要保证这2个性质不变.采用如下方法对原有的RIL进行改进.

对各个行业的RILl分别作一个变换fl，即

(5)

3实证分析

实证研究中主要研究沪深300样本股从2012年3月29日至2013年12月31日期间内RIL*值波动与股票市场波动性之间的关系.由于计算皮尔逊相关系数的需要，从雅虎数据库获取了2012年1月12日至2013年12月31日的沪深300的股指数据.由于节假日，停牌等因素会导致数据缺失，需要对缺失的数据进行补齐.对于连续缺失数据少于等于5天的股票，以日对数收益率为0进行补齐.对于缺失连续数据大于5天的情况，将该股从研究对象中剔除，最终得189支符合要求的股票.

从雅虎数据库下载得到的数据将股票行业分成75个行业，相对于我们研究的样本所含的股票数量来说，这个行业划分太细了，多数行业只含有1支股票.在文[6,12]中也遇到了这样的问题，他们对股票按照ISIC标准进行了重新分类.根据中华人民共和国国家统计局的《国民经济行业分类标准》将189支股票重新分为12个行业大类：“采矿业”，“制造业”，“电力、热力、燃气及水生产和供应业”，“建筑业”，“批发和零售业”，“交通运输、仓储和邮政业”，“信息传输、软件和信息技术服务业”，“金融业”，“房地产业”，“租赁和商务服务业”，“水利、环境和公共设施管理业”，“综合类”，最终对这12个行业大类分析其行业因素和股票波动性之间的关系.

3.1行业内部相关性分析

使用RIL工具分析2013年4月17日不同行业内股票相关性强弱.表1给出了2013年4月17日，12大行业的RIL和RIL*值.用原始的RIL工具来评价行业内部相关性强弱，有

RIL8>RIL9>RIL2>RIL1>RIL3>RIL4>RIL6

用改进后的RIL*比较，得

两个指标的排序结果存在差异.在使用原始的RIL指标比较时，制造业比采矿业的值高；在选用改进后的RIL*比较时，采矿业比制造业的值要高.这是因为原始的RIL指标没有排除标准值(第6列)不同的干扰.即对于不同的行业有不同的标准值，RIL指标不适合纵向比较.而改进后的RIL*指标统一了不同行业的标准值，使用它比较行业因素才是合理的.

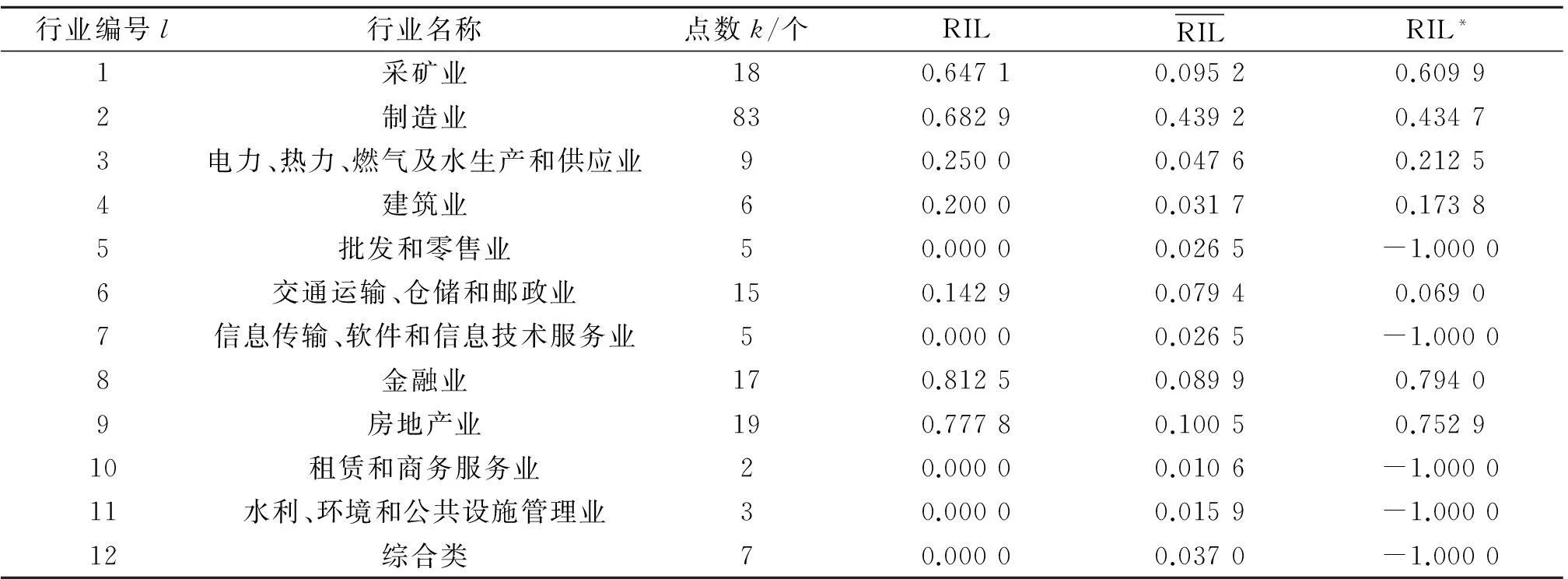
表1　各大行业的RIL和RIL*值

表2中的第7列给出了整个研究期内不同行业的RIL*均值(AvRIL*).从表2中可以看到：序号为5，7，10，11，12的行业，其RIL*标准值都为负值.这表示在整个研究期内，这5个行业内的各自股票都不具有相关性.在受行业因素影响的行业中以0.5为界，AvRIL*值大于0.5称为受影响强的行业，小于0.5称受影响一般的行业.

表2　行业因素影响均值分析

3.2RIL*和股票走势之间关系分析

序号为5，10，11的行业，由于没有与该行业划分相一致的指标所以无法进行比较评判.在建筑业的研究中我们没有发现该现象.而建筑业在整个研究期内行业因素影响强度只有AvRIL*=0.173 8，因此我们认为这个现象只存在于行业因素影响强的行业中.

图1　金融业行业RIL*和金融指数走势图Fig.1　RIL* value and financial index value for each day

4结论

在整个研究期内，“批发和零售业”、“租赁和商务服务业”、“信息传输、软件和信息技术服务业”和“水利、环境和公共设施管理业”这4个行业内的股票不具有相关性，因此也不存在行业因素的影响，其他7个行业内各自股票都有相关性存在.相比较而言，“金融业”、“采矿业”和“房地产业”在这段时期内，行业内部股票相关性最强，行业因素影响也是最强的.对于股票相关性强的行业，RIL*的走势出现剧烈下降时，该行业内的股票整体走势或剧烈上升或剧烈下降.

参考文献：

[1]CHING M M, SIOK K S. Comparing the performances of

GARCH-type models in capturing the stock market volatility in malaysia[J]. Procedia Economics and Finance,2013,5:478-487.

[2]MARK J J, JOHN M M. Estimating a semiparametric asymmetric stochastic volatility model with a dirichlet process mixture [J]. Journal of Econometrics,2014,178(3):523-538.

[3]GEORGE J J, YISONG S T. The model-free implied volatility and its information content[J]. Review of Financial Studies，2005,18(4):1305-1342.

[4]陈勇,胡婷婷,鲁建厦.基于遗传算法改进的动态车间调度[J].浙江工业大学学报,2012,40(5):537-553.

[5]余义龙,成丹丹,刘鸿鸣,等.具有长程记忆和市场判断力的异质经纪人Herding模型[J].浙江工业大学学报，2011,39(2)：231-236.

[6]胡永宏.农业上市公司股票的风险结构特征研究[J].数理统计与管理，2011,3(4):705-712.

[7]YE B, CHRISTOPHER J G, LAWRENCE L. Industry and country factors in emerging market returns: did the Asian crisis make a difference[J]. Emerging Markets Review,2012,13(4):559-580.

[8]史美景.随机效应方差分量模型及应用——股票换手率及行业因素对收益率影响的定量分析[J].山西财经大学学报,2002,24(1):99-101.

[9]MANTEGNA R N. Information and hierarchical structure in financial markets[J]. Computer Physics Communications,1999,121/122:153-156.

[10]CHI K T, JING L, FRANCIS C M. A network perspective of the stock market[J]. Journal of Empirical Finance,2010,17(4):659-667.

[13]MAMAN A D, SIEW L G. Optimality problem of network topology in stocks market analysis[J]. Physica A: Statistical Mechanics and its Applications,2015 419(1):108-114.

[14]施晓燕，周明华，李春艳.中国股指中保持概率的模型分析[J].浙江工业大学学报,2009,37(6):671-673.

(责任编辑：刘岩)

中图分类号：O29

文献标志码：A

文章编号：1006-4303(2015)03-0350-05

作者简介：周明华(1959—)，男，浙江绍兴人，教授，研究方向为金融数学，E-mail：mhzhou@zjut.edu.cn.

基金项目：浙江省重大科技专项计划项目(2011C11048)

收稿日期：2015-01-09