时域聚总、脉冲响应与中国经济波动的持久性特征研究
2015-02-18叶光
叶 光
(河南财经政法大学 经济学院,郑州 450046)
0 引言
宏观经济波动通常可视为经济系统受外生冲击影响后,实际产出对其潜在水平的短期偏离。对于外生冲击的来源,经济学界一般倾向于将其分为两类:供给冲击和需求冲击,前者对产出的影响是持久的,后者的影响是暂时的。因而,考察实际产出的动态特征及其对外生冲击反应的持久性,对于明确冲击的主要来源,进而制定和实施有效的反周期政策具有重要意义。但利用时间序列模型对此进行研究时,经常会面临不同频率样本数据的选择问题,按观测频率的不同,常用的样本数据有三类:月度、季度和年度数据,理论模型中任意相邻两期之间都是间隔一期,但这一期到底有多久却无从知晓,实际应用中研究者只能从时间跨度、样本容量和相关变量的数据可得性等方面来说明样本选择的合理性。样本观测频率的变化会改变时间序列模型的结构设定,从而对模型分析结果产生重要影响,即便使用同样的计量模型和分析方法,样本观测频率的不同也会导致估计结果差异很大,对此如何从理论上予以解释?不同估计结果之间存在着怎样的联系,如何从中探寻实际产出的真实动态特征?
时间序列从高频到低频的转换即为时域聚总,对于流量数据,低频数据为其观测时间间隔内所有高频数据的加总;对于存量数据,低频数据通常由每个时间间隔内最后一个高频观测值构成。现有研究表明,若高频序列的生成过程为(向量)ARIMA模型,则低频序列的模型形式保持不变,且具有相同的单位根性质和协整关系,但模型的自回归和移动平均结构会发生变化[1~5]这意味着利用脉冲响应函数考察经济序列的动态特征时,使用不同频率的样本数据可能会得到完全不同的估计结果。Rossana和Seater(1995)分别使用美国工业生产指数、失业率和利率等变量的月度、季度和年度数据估计ARIMA模型,考察样本观测频率变化对脉冲响应函数的影响,发现年度数据对应的脉冲响应函数非常平滑,而利用月度和季度数据估计的脉冲响应函数变化剧烈,形状上也比较接近。[6]脉冲响应函数反映了变量受到外生随机冲击后向均衡状态的收敛情况,对于特定的经济变量,样本观测频率的影响只能体现于不同频率的时间序列模型中“外生冲击”的差异,本文将从这个角度研究系统抽样对脉冲响应函数的影响,探讨不同观测频率下脉冲响应函数的理论联系。
对于经济变量对外生冲击反应的持久性,通常用累积脉冲响应(Cumulative Impulse Response,CIR)予以度量(Andrews和Chen,1994)。[7]如果对产出的对数差分序列(增长率)构建ARMA模型,将其转化为无穷阶MA模型后,相应的移动平均系数之和与CIR完全对应,其值为0意味着产出序列为趋势平稳过程,外生冲击主要源于需求层面,对产出的影响是暂时的(Compbell和Mankiw,1987)。[8]刘金全等(2007)对中国实际GDP季度增长率进行分析,发现外生冲击对中国实际产出的影响具有较强的持久性,这与孙晓涛、王少平(2012)的结论基本一致,但二者关于持久性程度的估计结果有一定区别。[9][10]样本观测频率变化时,脉冲响应函数的差异本身就意味着CIR的不同,但理论上,经济变量的持久性特征是既定的,不因数据频率变化而改变。二者的矛盾说明,现有文献用CIR或移动平均系数之和度量变量的持久性特征的做法是值得商榷的,在此基础上对经济波动持久性的研究也不够可靠。正基于此,本文将从理论上研究时域聚总对脉冲响应函数和累积脉冲响应的影响,明确累积脉冲响应与样本观测频率的关系,探寻更加稳健的关于经济变量持久性特征的度量方法,在此基础上分别使用月度、季度和年度数据估计国内产出对外生冲击的动态响应路径,为理论研究提供经验支持的同时,更加全面地揭示中国经济波动的持久性特征。
1 时域聚总对脉冲响应函数和累积脉冲响应的影响
1.1 对数差分序列ARMA模型的时域聚总问题
令{xt}表示高频时间序列,每隔k期得到一个低频观测值,k为大于1的整数,相应的低频序列用{XT}表示。从T-1期到T期,低频观测值只有一个XT,高频观测值则有k个:x(T-1)k+1,x(T-1)k+2,…,xTk,两者的关系即从低频序列到高频序列的聚总机制,可以设定为:

其中,L 为t刻度下的滞后算子,xt-1=Lxt,XT-1=LkXT,Lk为T刻度下的滞后算子。对于存量数据,W(L)=1;对于流量数据,W(L)=1+L+…+Lk-1。在关于经济波动持久性和其他很多实证研究中,需要使用对数差分序列(增长率)构建ARMA模型,将{xt}和{XT}的增长率序列分别表示为{yt}和{YT},若x为存量,式(1)中聚总机制对于对数差分后的序列同样成立,但若x为流量,需要利用式(1)重新设定yt和YT的关系。考虑到中国宏观数据的官方发布情况和季节性因素,本文使用同比增长率进行分析。令同比增长率YT=(XT-XT-j)/XT-j,对于季度和年度序列,j分别为4和1,由式(1)可以得到:

其中,ωT为T刻度下的扰动项。若y为存量,式(5)中MA项的滞后阶数为p(k-1)+q,所有大于p(k-1)+q阶的自相关系数全部为零,要保证与之相同的自相关结构,式(6)中MA项的滞后阶数r应该等于int[(p(k-1)+q)/k],int为取整函数;若y为流量,r为int[((p+1)(k-1)+q)/k](Amemiya和Wu,1972)。[1]从式(4)和式(6)中自回归系数的关系可以看出,时域聚总不影响序列的单位根性质,且当k有限时,模型的自回归阶数也不发生变化。但对于平稳序列,|li|<1,式(4)中高阶自回归系数非常接近于0,因而实际应用中,利用低频序列选择的滞后阶数往往远小于高频序列。
1.2 时域聚总对脉冲响应函数的影响
分别利用式(5)和式(6)对YT进行预测,令高频序列的已知信息集为Ωh={yTk-1,yTk-2,…},低频序列的信息集Ωl={YT-1,YT-2,…},通过式(3)可以从 Ωh得到 Ωl,反之则不成立,这意味着高频序列比低频序列包含更多的数据信息。由此可以将扰动项εTK和ωT分别表示为:
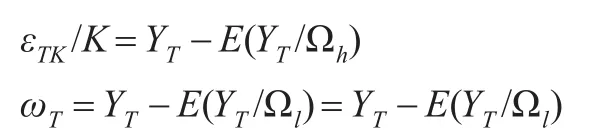
也即是说,两个扰动项都可视为对YT的预测误差,区别在于已知的信息集不同。进行脉冲响应分析时,高频序列模型中外生冲击来自于信息集Ωh之外的不可预测因素,而对于低频序列,则是Ωl之外的不可预测因素,两种模型中关于“外生冲击”界定的差异必然会导致脉冲响应函数的不同。实证研究中利用不同频率的样本数据,通常会发现变量对单位外生冲击有着完全不同的响应,过多关注脉冲响应函数的具体数值没有实际意义。
利用脉冲响应函数考察外生冲击影响的持续时间。若高频序列模型为MA(q)过程,外生冲击的影响持续q期,则相应的低频序列模型中MA阶数和外生冲击影响的持续期都为int[(q-1)/k]+1,换算为高频序列的时间单位,低频序列模型中外生冲击影响的持续时间大于或等于高频序列模型,但差距在k期之内。对于一般的ARMA模型,脉冲响应函数的尾部值主要决定于AR多项式的最大根,结合式(4)和式(6)中自回归系数的关系可以看出,当et对yt的影响衰减到接近于零时,wT对YT的影响也应该与零非常接近。
1.3 时域聚总、累积脉冲响应与持久性的度量
假定yt是协方差平稳的,系统抽样不改变序列的平稳性,YT同样协方差平稳,根据Wold分解定理,给出式(4)和式(6)的MA(∞ )形式:
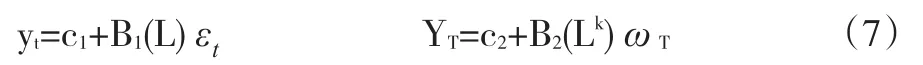
其中,c1、c2和B1(L)、B2(Lk)中诸多参数分别为式(4)和式(6)中参数的函数。从而高频和低频序列模型中CIR分别为B1(1)和B2(1)。利用自协方差生成函数得到:
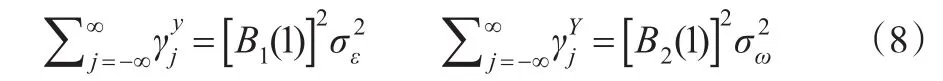
这里gjy和gjY分别表示yt和YT的j阶自协方差;σε2和σω2为扰动项ε和ω的方差。
定义与yt具有相同观测频率的高频序列{Yt*},其每个观测值皆为{yt}中前k期观测值的样本均值,将式(7)中yt的方程两侧同乘以W(L)/k,同样利用自协方差生成函数得到:
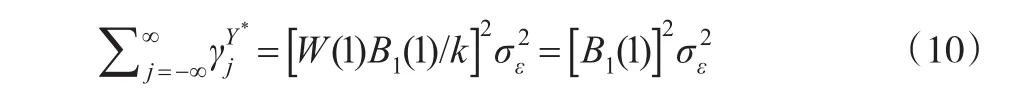
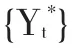
考虑到YT可近似表示为yt中前k期值的算术平均,利用不同频率的样本数据估计CIR时,为对估计结果进行比较,建议将高频序列的CIR除以k。但由于式(4)和式(6)中单位冲击的含义不同,这种做法也只能部分消除时域聚总的影响。由此可见,在使用调整后的CIR对持久性予以度量的基础上,进一步通过脉冲响应函数考察经济变量受到外生冲击后向其均值的收敛时间,在此基础上研究其持久性特征理论上更为可取。
2 样本观测频率与中国经济波动的持久性
2.1 数据来源与统计特征
为更好地说明时域聚总的影响,本文选取月度数据可获取的工业增加值数据来研究产出波动的动态特征。工业增加值实际同比增长率直接源于国家统计局公布的“规模以上工业企业增加值当月同比实际增速”,时间跨度是1990年10月到2014年12月。由于其1、2月份数据受春节因素影响很大,国家统计局不发布1月当月数据,自2013年起,2月份当月数据也不再发布,本文以1-2月份累计同比增速作为2月份当月数据,1月份数据由插值估算。图1给出了三种观测频率下中国工业增加值同比增速的变化特征,三者具有非常类似的长期趋势,但从短期变化来看,观测频率越高的序列短期变化越剧烈。
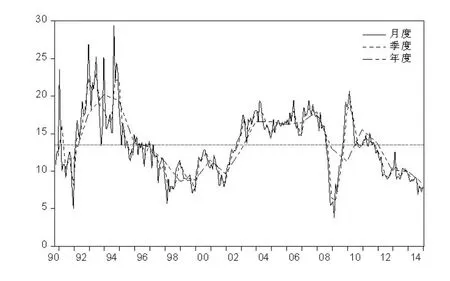
图1 不同频率下中国工业增加值同比增速的变化特征
从图1可以看出,从上世纪90年代初期的高通胀阶段之后,到2008年全球金融危机爆发之前,中国经济先后经历了持续时间很长的低速调整时期和高速增长时期。前者从1996年开始到2002年结束,共持续了8年,主要归因于国内长期实施的经济“软着陆”政策和1998年亚洲金融危机的影响。2003年之后,在出口拉动和“双稳健”政策的共同作用下,中国经济开始了持续5年的高速增长时期。2007年下半年国内经济开始面临较大的通胀压力,特别是房地产价格的居高不下,迫使政府出台了一系列的调控措施,但并没有取得理想的实际效果。直到2008年在美国金融危机和“从紧”货币政策的双重压力下,经济增速出现了近20年来最严重的下滑,中国经济开始由高速增长转向低速调整的“新常态”阶段。总体来看,中国的经济波动表现出了比较明显的强持久性,供给层面的冲击可能是国内经济波动的主要来源,在供给层面整体不够健全的情况下,4万亿投资计划仅带来了2009年昙花一现的恢复,单靠需求管理政策已经很难保证中国经济的平稳快速发展。因而,新一届政府开始将政策着力点由需求管理转向供给管理,注重经济结构调整和企业自主创新能力的培养。

表1 中国工业增加值同比增长率序列的ADF单位根检验
对工业增加值同比增长率序列进行ADF单位根检验,结果如表1所示。样本观测频率的变化不改变序列的单位根性质,表中基于月度和季度数据的检验结果完全一致,即在5%显著水平下拒绝存在单位根的零假设,1990年以来中国工业增加值的同比增长率序列是平稳的。我们也对年度序列进行了单位根检验,利用AIC准则选择的滞后阶数为3,ADF统计量值为-2.83,p值为0.07,但由于年度数据的样本容量仅为24,这种情况下单位根检验的功效很低,实际检验水平的扭曲也比较严重。如果适当提高检验水平,在10%水平下依然可以认为序列是平稳的。因此,本文将直接对工业增加值同比增长率序列构建ARMA模型,在此基础上研究中国经济波动的持久性特征。
2.2 中国经济波动的动态特征
2.2.1 经济波动的持久性
假定工业增加值同比增长率序列的真实过程为ARMA模型,时域聚总不改变模型形式,对于月度、季度和年度序列,都可以使用ARMA模型进行拟合。但当样本观测频率发生变化时,模型的自回归阶数p和移动平均阶数q会随之改变,在确定滞后阶数时,主要关注序列相关检验的Q统计量值,以保证扰动项的白噪声性。如果满足条件的滞后阶数不唯一,选择AIC准则取值最小者。对于模型中可能存在的不显著项,若将其删除会导致序列相关,则予以保留。表2给出了与三种频率样本数据相对应的模型滞后阶数、估计结果和相关统计量的值,从Q统计量的表现来看,表中滞后阶数的设定足以消除模型的序列相关性。
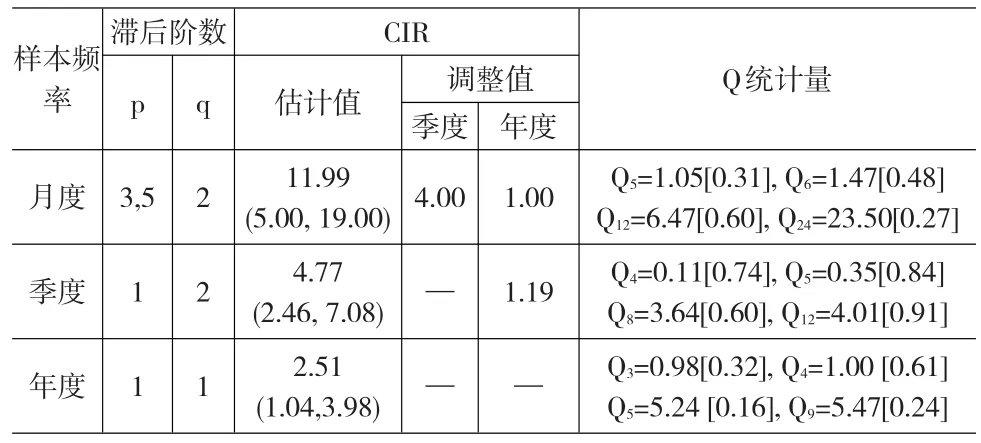
表2 不同样本观测频率下中国经济波动持久性的估计值(1990-2014)
由于不同频率的ARMA模型中扰动项的方差不同,为便于比较,我们通过考察单位冲击的影响来计算累积脉冲响应(CIR)。从表2可以看出,CIR的估计值与数据频率密切相关,数据频率越高,估计结果越大,与前文理论分析的结论保持一致。使用月度数据估计的CIR最大,为11.99,但随着观测频率的降低,其数值不断减小,季度数据的估计值减小到4.77,年度数据进一步下降到2.51。这一方面说明无论使用何种频率的样本数据,都能发现中国的经济波动具有较强的持久性,另一方面则意味着,忽略样本观测频率的差异,仅关注CIR所反映的持久性程度,很难真正揭示经济波动的动态特征。
将月度序列聚总为季度序列时,式(3)中k等于3,为此我们以月度CIR除以3作为调整到季度水平的CIR,调整后的估计值为4.00,与直接使用季度模型得到的估计值非常接近。对于年度水平的CIR,利用月度或季度模型得到的调整值比较接近,但都明显低于基于年度模型的估计结果,其原因有两点:一是与月度或季度序列相比,年度序列损失了大量的数据信息,从而脉冲响应分析中单位冲击的含义明显不同;二是年度数据的样本容量较小,模型估计结果可能存在较大误差。但总体来看,调整后的估计值受样本观测频率的影响明显减弱,对不同观测频率下CIR的估计结果进行比较时,调整后的结果更具有可比性。此外,虽然表2中调整后的估计结果比较接近,一定程度上揭示了中国经济波动的持久性特征,但这也只能告诉我们外生冲击的影响会持续一段时间,但具体有多久,还需要借助脉冲响应函数进一步研究。
2.2.2 脉冲响应函数
图2描绘了利用月度、季度和年度数据估计的脉冲响应函数,横轴刻度为月份。除初始阶段略有差异之外,月度和季度数据对应的脉冲响应函数比较接近,半衰期分别为7个月和9个月,第3年末大致收敛到均衡状态。利用年度数据估计的脉冲响应函数数值上明显大于月度和季度数据的估计结果,半衰期接近2年,但同样在第3年末收敛到均衡状态。如果仅仅关注外生冲击的持续时间,从图2可以看出,使用不同频率的样本数据所得到的结论基本一致,这与前文的理论分析非常吻合。相对而言,年度脉冲响应函数的时间跨度过大,很难真正表现出经济变量对外生冲击的短期动态反应,当我们主要关注这种动态响应路径时,利用月度数据或季度数据进行脉冲响应分析显然更为可取。
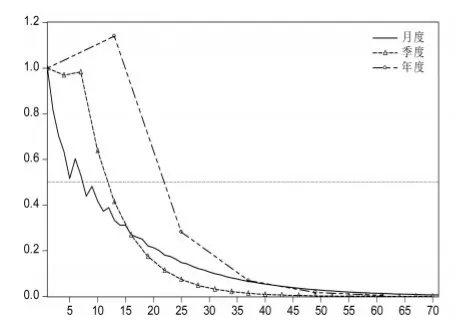
图2 不同样本观测频率下的脉冲响应图
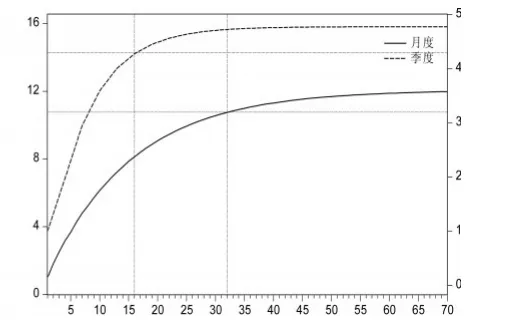
图3 月度与季度累积脉冲响应图
由于脉冲响应函数通常呈指数衰减,很难精确判断具体的收敛时间,从可操作性角度看,人们可能更关心外生冲击的影响绝大部分在多长时间内实现。图3描绘了中国工业增加值同比增速的月度和季度累积脉冲响应图,分别对应着左侧和右侧纵轴,横轴刻度为月份。虽然二者脉冲响应函数比较接近,但累计脉冲响应函数存在比较明显的差异。图中二者实现最终收敛值的90%部分所需要的时间分别为16个月和32个月,相差整整1倍。对于年度脉冲响应函数,实现90%影响的时间在2年和3年之间。在缺乏进一步信息来判断哪个结论更为准确的情况下,只能得到一个比较宽泛的区间,即外生冲击对中国实际产出的影响大致需要经过1年半到3年的时间才能完全实现。
外生冲击对中国经济的影响大致会持续3年左右,半衰期接近2年,说明中国的经济波动具有较强的持久性。这种持久性一定程度上源于长期实施的“软着陆”和“软扩张”调控政策,但不能因此忽略中国经济自我调整和稳定机制的欠缺。因而,“新常态”下政府不仅要着力调整经济结构和转变经济增长方式,还要切实减少对市场主体微观经济行为的过度干预,不断完善市场体系,真正发挥市场在资源配置中的作用,逐步提高经济的自我调节能力。
3 结论
本文针对常用的ARMA模型,从理论上探讨时域聚总对脉冲响应函数和累积脉冲响应的影响,在此基础上全面考察中国经济波动的持久性特征。主要结论如下:
累积脉冲响应通常会随着样本观测频率的提高而增加,直接用其度量变量的持久性特征并不可取。研究经济波动的持久性特征时,为保证不同频率样本数据的估计结果具有可比性,建议将利用高频序列估计的累积脉冲响应除以k。系统抽样对脉冲响应函数的影响主要在于“外生冲击”界定的不同,实证研究中过多关注脉冲响应函数的具体数值意义不大,但可以通过脉冲响应函数考察外生冲击影响的持续时间,其反应的持久性特征理论上更为可信。
关于经济波动持久性的研究表明,外生冲击对中国经济的影响大致会持续3年左右,半衰期接近2年,中国的经济波动具有较强的持久性,供给层面的冲击是国内经济波动的重要原因。政府在将政策着力点由需求管理转向供给管理的同时,还要切实减少对市场主体微观经济行为的过度干预,不断完善市场体系,真正发挥市场在资源配置中的作用,逐步提高经济的自我调节能力。
[1]Amemiya T,Wu RY.The Effect of Aggregation on Prediction in The Autoregressive Model[J].Journal of The American Statistical Association,1972,(339).
[2]Brewer K R W.Some Consequences of Temporal Aggregation and Systematic Sampling for ARMA and ARMAX models[J].Journal of Econometrics,1973,(1).
[3]Weiss A A.Systematic Sampling and Temporal Aggregation in Time Series Models[J].Journal of Econometrics,1984(3).
[4]Granger C W J,Siklos P R.Systematic Sampling,Temporal Aggregation,Seasonal Adjustment,and Cointegration[J].Journal of Econometrics,1995(1).
[5]Marcellino M.Some Consequences of Temporal Aggregation in Empirical Analysis[J].Journal of Business&Economic Statistics,1999(1).
[6]Rossana R J,Seater J J.Temporal Aggregation and Economic Time Series[J].Journal of Business&Economic Statistical,1995(4).
[7]Andrews D W K,Chen H Y.Approximately Median-Unbiased Estimation of Autoregressive Models[J].Journal of Business&Economic Statistical,1994(2).
[8]Campbel J,Mankiw G. Permanent and Transitory Components in Macroeconomics Fluctuations[J].The American Economic Review,1987(2).
[9]刘金全,刘志刚,李庆华.我国实际产出序列的周期成分分解与周期波动的持久性度量.中国数量经济学会.21世纪数量经济学[C].北京:社会科学文献出版社,2008.
[10]孙晓涛,王少平.我国的经济波动来自供给冲击还是需求冲击?——对我国GDP波动持久性的度量.中国数量经济学会.21世纪数量经济学[C].北京:社会科学文献出版社,2013.
