贝叶斯偏正态线型混合模型的应用

王明高

（1.山东工商学院 统计学院，山东 烟台 264005；2.中国人民大学 统计学院，北京 100872）

0 引言

线性混合模型经常用于分析重复观测的纵向数据，在很多领域如农业、生物、卫生、经济、保险精算等都有广泛应用。线性混合模型在线性解释变量中包含随机效应，随机效应不但可以考查同类观测值之间的相关性结构，还可以考虑不同类别的异质性。该模型具有广泛的应用，主要是他们建模的灵活性，可以处理对称数据和非对称数据，而且存在比较有效的软件来拟合线性混合模型。

线性混合模型是线性模型的扩展，假设一个具有m个类别的数据，每类数据具有ni个个体i=1，…，m，假设Yi是一个对样本i连续性测量的ni维向量。则Yi所具有的线性混合模型一般表达式为：

虽然上面讨论的模型对纵向数据建模具有很大的灵活性，但是对于偏离假设分布情况，他们缺乏相应的稳健性。假设随机效应和响应变量(随机误差)都服从正态分布并不适合所有数据，比如响应变量为计数数据、二元数据和偏态数据等，并且随机效应不能保证服从对称的正态分布。对标准线性混合模型的扩展在一些文献中涉及，主要是用不同的分布来代替随机效应的正态分布假设，如Zhang(2001)[1]Ghidey(2004)[2]等。这些文章中有一个共同点就是对误差都假设服从正态分布。在涉及连续性测量时，对个体之间的分布假设为正态分布在大多数的情况下比较合理，在其他一些情况下需要进行转换来满足正态分布假设，比如对数据进行对数变换。虽然这些方法可以给出比较合适的实证结果，对数据进行转换可能使原来数据潜在生成机制提供的信息减少，另外数据转换适用于单个个体，不能保证联合正态性，还有转换后的变量比较难以解释。所以对数据进行建模时要根据数据的分布形式，选择合适的模型进行评估，如果存在更加合适的理论模型我们尽量避免对数据进行变换。

基于以上原因，本文探讨对线性混合模型随机效应和误差效应的非正态假设。介绍更加灵活的分布处理非正态分布的这种情况，而不去进行特别的数据变换。

1 偏正态分布

本文主要研究偏正态分布，偏正态分布在很多文献中都有涉及，在这里介绍Arellano-Valle(2007)[3]、Arellano-Valle(2005)[4]和 Sahu(2003)[5]、Azzalini(1999)[6]、Azzalini(1996)[7]中所介绍的偏正态分布及其相应的特征。

1.1 一元偏正态分布

假设X是一个连续随机变量，服从偏正态分布则概率密度函数是：

偏正态分布的一个重要性质就是各阶矩都存在，矩母函数如下所示：

偏正态分布可以认为是对正态分布的扩展，一元偏正态分布的曲线如图1所示，该图显示δ（σ=1，μ=0）取五个不同值的图形分布情况，当δ=0时曲线表示对称分布标准正态分布，其他δ值的曲线呈现偏态分布。

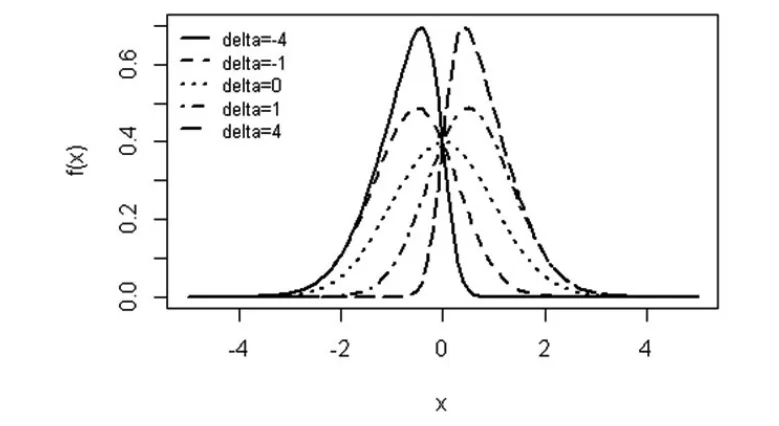
图1 偏正态分布曲线图

从上面公式可以看出，偏正态分布的表达式比较复杂，这就给模型的建模带来困难，但是通过对模型进行转化，可以使该分布通过两个相互独立的正态随机变量来获得偏正态分布随机变量。Henze(1986)[8]一文对一元偏正态分布的随机化表述做了一些研究，偏正态分布形式也可以写成如下等价形式：

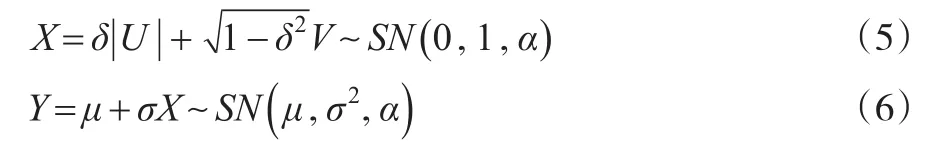
这里U和V是相互独立的标准正态随机变量，由和所表示的等价形式简化了偏正态分布函数，便于对偏正态分布混合模型建模。

1.2 多元偏正态分布

2 偏正态线性混合模型

2.1 偏正态线性混合模型简介

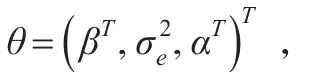
本模型主要目的是估计参数本文是在贝叶斯框架内对线性混合模型进行推断分析，这种模型的推断是建立在响应变量Y的分布基础之上，该线性混合模型的随机效应和误差项可以服从一元或多元偏正态分布，这个模型的一个重要优势就是可以用来评估偏态非对称数据，随机效应并不局限于服从对称的正态分布。

2.2 贝叶斯偏正态线性混合模型

要写出各参数的条件分布。这种算法在开始的时候需要给出所有随机变量的初始值，再由条件分布生成样本，直到样本收敛。我们可以用Gelman(1992)[11]定义的统计量检验所生成的样本是否收敛。

3 应用

3.1 雇主责任险的案例

本文引用一个雇主责任险的案例，该险种主要处理永久性或部分丧失工作能力的索赔，在这个纵向数据中共有121个职业分类即风险类别，在7年观察期内发生的847条数据。这些数据包括职业类别、观察年、收入和赔付额。在Frees(2001)[12]的论文中分析了这些数据，他选用纯保费(PP=Loss/Payroll)为响应变量即赔付额与收入的比率，解释变量有观察年、职业类别。Frees(2001)[14]在建立模型时没有直接用纯保费数据，而是使用纯保费的对数数据。从图2的左侧纯保费频率分布图可以看出，纯保费是一个右偏的分布图形。将纯保费数据进行对数变换，对数变换后的数据分布如图2右侧所示，该图呈现出类似正态分布的对称分布图形。

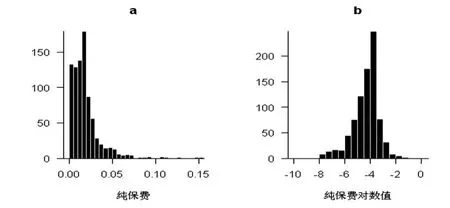
图2 纯保费直方图

这些变量的取值在Frees(2001)[12]文章的第四部分中的表3有描述，该表显示观察期内所有职业的平均收入为195百万美元，平均纯保费为0.0203。从表中可以看出平均保费没有呈现随观察年变化的趋势，收入表现出随观察年增加的趋势。另外部分职业的纯保费随观察年的变化如图3所示，我们可以看出纯保费并不随观察年变化，但是纯保费对数值的波动情况跟纯保费的波动情况不同，纯保费随观察年的变化偏向一侧，纯保费对数值呈现对称波动。

图3 部分职业的纯保费随观察年的变化趋势

上面这种表示方式比较重要，因为有利于用BUGS编写程序。应用Gibbs抽样需要得到各参数的条件分布，根据各参数的条件分布进行抽样。但是本文应用Open-BUGS软件，只需要根据模型的分层结构进行编程，没有必

虽然纯保费跟观察年之间没有明显的变化趋势，但是该数据是纵向数据，需要考虑同一组数据之间的相关性。在该数据中同一职业类别不同观察年之间的观察值具有显著地相关性，在建立模型时需要考虑这些问题。

3.2 态线性混合模型的建立

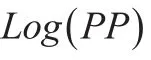
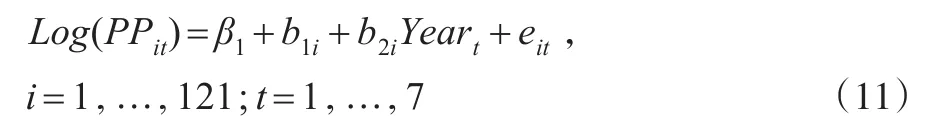
本文应用偏正态分布定义随机效应bi和随机误差项eit构成偏正态线性混合模型，本文将通过三个模型进行比较分析。第一个模型是一般的线性混合模型，响应变量为纯保费的对数值，随机效应和随机误差项服从正态分布。第二个模型引入偏正态分布，假设随机误差项服从偏正态分布，随机效应服从正态分布，响应变量为纯保费。第三个模型的随机误差项和随机效应都服从偏正态分布，响应变量为纯保费。

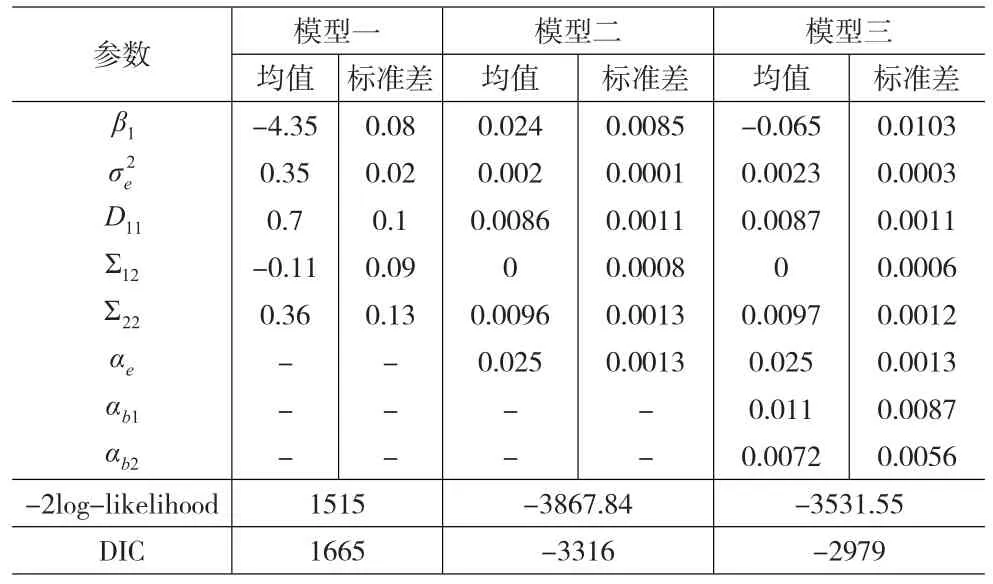
表1 三个模型参数的后验分布得出均值与标准差

为了选取合适的模型我们需要对模型进行比较分析，贝叶斯模型的评估结果用DIC统计量Spiegelhalter(2002)[13]进行比较分析，模型DIC表达式如下所示：

另外对模型的残差考查如图4、图5所示，这两个图只给出模型一和模型二的残差图，其中左边的a图是模型一的残差图，右边的b图是模型二的残差图。从这两图中可以看出模型一的残差具有一定的异方差性，残差波动范围比较大，其变化范围超过了模型响应变量纯保费的取值范围。模型二的残差波动范围比较小，而且残差主要聚集在零值附近，说明该模型二很好的拟合了该数据。另外图6表示纯保费与其模拟值之间的散点图，可以看出由b图所表示的模型二拟合效果明显好于a图所表示的模型一，模型二给出的模拟值能够很好地近似实际的纯保费数据。从下面的图形我们可以看出假设随机误差服从偏正态分布的模型能够更好的反映实际数据。

图4 纯保费对残差的散点图

图5 损失对残差的散点图

图6 纯保费对其模拟值的散点图

4 结论

本文主要研究如何更好对具有非对称分布特征的纵向数据进行建模，传统的方法一般对数据进行变换，比如对数变换等。但是对数据进行变换可能损失一些信息，本文探讨引入适合所分析数据特征的分布来处理非对称数据。

在文中引用一个具有右偏特征的保险损失数据，在Frees(2001)文中通过对数变换来处理该数据的右偏性，应用线性混合模型来分析，本文根据所选数据的分布特征，选用可以处理偏态数据的偏正态分布，建立偏正态线性混合模型，并且与对数变换的线性混合模型进行比较，评估结果得出偏正态线性混合能够更好拟合该数据。通过本文的一个实例数据分析发现，对一些非对称数据的建模，应用非对称模型更加有效。实际上一般线性混合模型假设随机效应和随机误差服从正态分布，可以认为是对偏正态分布线性混合模型的特殊情况。

虽然所涉及的线性混合模型比较复杂，本文应用贝叶斯蒙特卡罗方法Gibbs抽样对偏正态线性混合模型的参数进行估计，这种方法可以通过免费软件OpenBUGS非常方便的得出相关结果。本模型估计一个比较大的优势就是可以对模型的随机效应和随机误差给出更加灵活的假设。通过本文的分析可以发现，基于贝叶斯方法的偏正态线性混合模型处理纵向数据，使模型不再局限于传统的假设，可以建立符合实际数据特征的混合模型，从而能够更好的处理所研究数据。

[1]Zhang D,Davidian M.Liner Mixed Models With Flexible Distributions of Random Effects for Longitudinal Data[J].Biometrics,2001,（57）.

[2]Ghidey W,Lesaffre E,Eilers,P.Smooth Random Effects Distribution in A Linear Mixed Model[J].Biometrics,2004,（60）.

[3]Arellano-Valle R B,Bolfarine H,Lachos V H.Bayesian Inference for Skew-Normal Linear Mixed Models[J].Journal of Applied Statistics,2007,（34）.

[4]Arellano-Valle R B,Genton M G.Fundamental Skew Distributions[J].Journal of Multivariate Analysis,2005,（96）.

[5]Sahu S K,Dey D K,Branco M.A New Class of Multivariate Distributions With Applications to Bayesian Regression Models[J].The Canadian Journal of Statistics,2003,（29）.

[6]Azzalini A,Capitanio A.Statistical Applications of The Multivariate Skew-Normal Distributions[J].Journal of The Royal Statistical Society,1999,（61）.

[7]Azzalini A,Dalla-Valle A.The Multivariate Skew-Normal Distribution[J].Biometrika,1996,（3）.

[8]Henze,N.A Probabilistic Representation of The Skew-Normal Dis-Tribution[J].Scand J Statist,1986,（13）.

[9]Arellano-Valle R B,Azzalini,A.On The Unification of Families of Skew-Normal Distributions[J].Scand J Statist,2006,（33）.

[10]Azzalini,A.The Skew-Normal Distribution and Related Multivariate Families[J].Scandinavian Journal of Statistics,2005,32(2).

[11]Gelman A,Rubin D.Inference From Iterative Simulation Using Multiple Sequences[J].Statistical Science,1992,（7）.

[12]Frees E W,Young V R,Luo Y.Case Studies Using Panel Data Models[J].North American Actuarial Journal 2001,5(4).

[13]Spiegelhalter D J,Best N G,Carlin B P,Van Der Linde,A.Bayesian Measures of Model Complexity and Fit(With Discussion)[J].Journal of The Royal Statistical(B),2002,（64）.