变系数部分线性模型的估计有效性研究

赵文星，程国胜，来 鹏

（南京信息工程大学数学与统计学院，南京 210044）

0 引言

在现今统计分析中，往往希望建立的模型既准确又易于解释。事实上，研究的大多数模型既含有参数分量又包含非参数分量，尤其在计量经济学和生物医学等领域，变系数部分线性模型被广泛应用。它的优势在于既结合了线性模型的易于解释，又可以描述协变量的交互影响，此外，该模型允许更灵活的函数形式，同时还能降低数据的维数。为此，有必要对其进行研究。变系数部分线性回归模型可以定义如下，

其中，Y是响应变量，X和Z分别为 p维和q维向量，t是一维变量，g(·)是一个未知的可测函数，随机统计误差 ε满足 E(ε|X，Z，t)=0 和 var(ε|X，Z，t)=σ2(X，Z，t)。在模型(1)中，参数部分βTZ提供了协变量的线性组合，回归系数gj(t)依赖于t，j=1，…，p，具有灵活的模型形式且避免了“维数祸根”。模型(1)包含了常用的线性模型、变系数模型和部分线性模型等半参数和参数模型，使得其具有广泛的应用领域。自从该模型被提出以来，变系数部分线性模型被广泛研究并应用在各种领域。

模型参数的优良估计应该满足无偏性与相合性外，还应考虑所得估计是否能有效地帮助实际工作者得到更准确的估计。半参数模型估计的有效性是评价估计优劣的一个重要性质，例如Tsiatis(2006)等[1]从模型参数的有效得分函数出发研究了参数模型估计的有效性。在Liang等[2]提出估计的基础上，Härdle[3]提出了一种加权扩展估计，利用方差的倒数作为逆概率的权重，提高了部分线性模型参数的估计效率。但是，Ma等[4]中指出他们所提出的估计仍然不是最有效的估计，为此，Ma等通过计算部分线性模型的有效得分函数，利用它构造有效估计方程，从而求出带有异方差的部分线性模型的半参数有效估计。从这些文章中，可以发现有效得分函数对于得到有效估计有着非常重要的作用。为此，本文通过推导带有异方差的变系数部分线性模型的有效得分函数来构造有效估计方程，给出带异方差的变系数部分线性模型的半参数有效界，证明所得估计为有效估计，并证明其大样本性质。

1 估计方程和有效估计

从模型(1)中可以看出，参数β是感兴趣的参数，而系数函数 gj(·)，(j=1，…，p)，未知的异方差函数 σ2(X，Z，t)，(ε|X，Z，t)的条件分布和 (X，Z，t)的边际联合分布均为冗余参数。由Tsiatis等(2006)[4]可知，若可以得到有效得分函数，则可以利用其构造有效估计方程，计算得出有效估计。为此，需要先求解有效得分函数，通过计算和推导证明，可以得到如下定理，（定理证明略）。

定理1设在给定(X，Z，t)下，ε的条件概率密度函数为 pε(ε|X，Z，t)，并且 pε(ε|X，Z，t)关于 ε可导，几乎处处有0＜E(ε2|X，Z，t)＜∞ 。那么模型(1)的半参数有效得分函数是

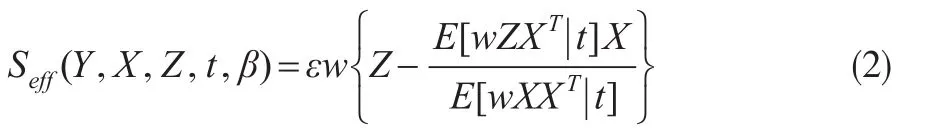
其中，w=w(X，Z，t)={E(ε2|X，Z，t)}-1，ε=Y-gT(t)X-βTZ 。

从中可以知道，正则的渐近线性估计与它所对应的影响函数是一一对应的，也就是说利用有效影响函数可以找到有效估计。而在上述定理中已经得出了变系数部分线性模型的有效得分函数，根据有效影响函数与有效得分函数之间成正比例的关系，自然的可以利用有效得分函数来构造估计方程。根据(2)式可以建立如下估计方程：

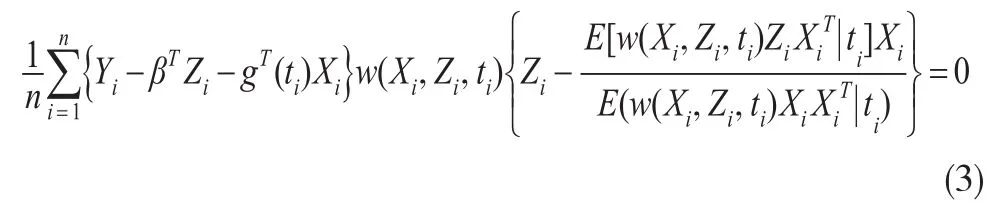
由有效得分函数与有效估计的一一对应性，通过对(3)式估计方程的求解可以得到β的半参数有效估计。但是，从方程(3)中可以发现，其中包含了未知的函数 g(·)，w(·)，E[w(X，Z，t)ZXT|t]和 E(w(X，Z，t)XXT|t)，这些未知函数会影响方程的求解。因此，首先需要对这些未知函数进行相应的估计，以便将方程中的未知量用其估计值进行插值替换，从而便于对感兴趣的参数进行求解。注意到可以将模型(1)写成

根据所得估计的渐近方差V，可以发现β^的渐近方差阵等于半参数有效得分函数Seff(·)的协方差矩阵的逆，由此依据Tsiatis[6]中的定理4.1可知，所得估计的渐近方差达到半参数有效界，所以通过求解估计方程(9)得到的估计为带异方差的变系数部分线性模型的半参数有效估计。

2 模拟仿真

为了研究所提出估计的有限样本性质，判断其是否为有效估计，本文用数值模拟来说明所提出估计的优劣，并与其他几种估计方法所得的估计进行比较。

考虑对以下几种估计方程所得β的估计进行比较：

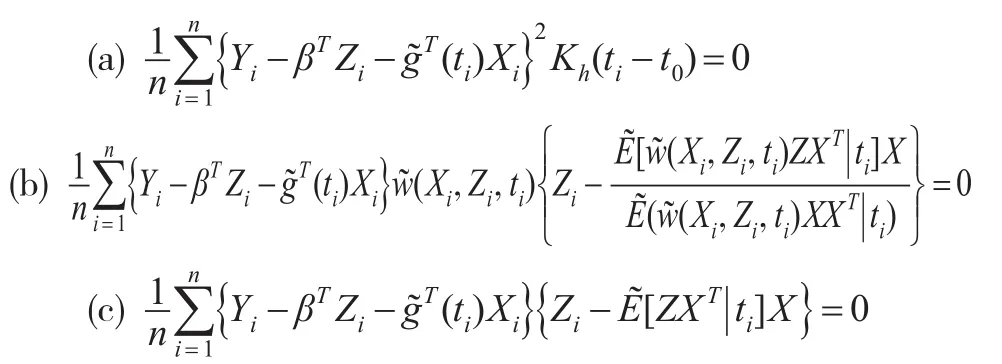
为了比较不同估计方程所得估计的优劣，本文通过所得估计的偏差(Bias)、标准差(SE)和均方误差(MSE)来进行比较。例1和例2所得模拟结果见表1和表2所示。

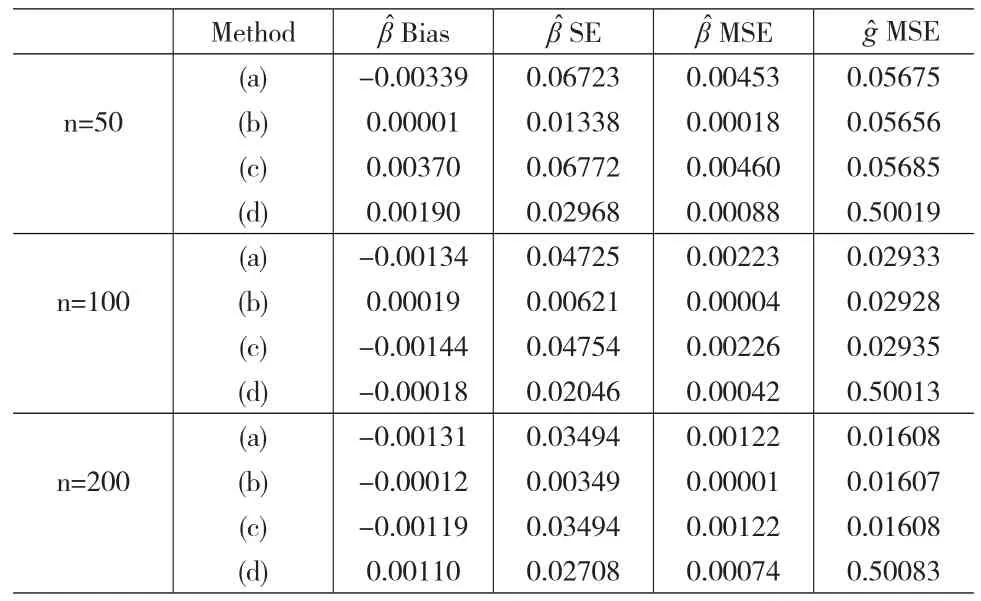
表1 例1所得模拟结果

从表1和表2可以看出，当采用估计方程的方式求解估计时，随着样本量的增加，总的来说各个加权估计方程解出的估计值β^的偏差、标准差和均方误差均是越来越小，并且由表1和表2中估计的标准差和均方误差可以发现，本文所提出的估计方法(b)比其它估计方法更优越，所得的标准差(SE)和均方误差(MSE)都是最小的。因此，本文提出的利用有效得分函数构造加权有效估计方程的方法能够提高估计的效率，并且具有较小的偏差，可以得到最有效的的估计。

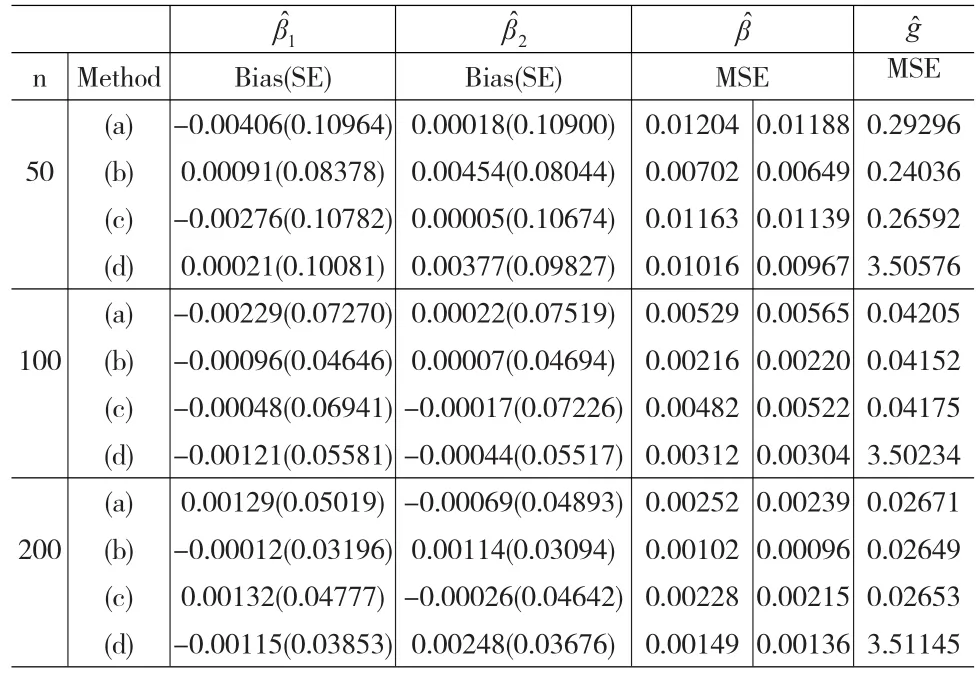
表2 例2所得模拟结果

3 结论

本文推导得到带有异方差的变系数部分线性模型的半参数有效界，通过导出的感兴趣参数的有效得分函数，构造有效估计方程，并由此来进行参数估计。通过大样本下的理论性质的证明，以及通过小样本下的数值模拟，可以得到所提出的估计求解方法能够得到一致较优的有效估计。同时，注意到在对感兴趣的参数进行估计之前，先是要对模型中其它未知函数进行估计，在仿真模拟中可以发现，这些未知参数估计所采用的不同非参数估计方法不会影响到感兴趣参数的估计效率。从数值模拟中还可以看出，本文所提出的估计方程得到的估计的偏差、标准差和均方误差随着样本量的增加，逐渐减小且小于其它方法所得估计值。由此可知，本文所提出的方法是有效的且有较强的稳健性。

[1]Wahed A S,Tsiatis A A.Semiparametric Efficient Estimation of Survival Distributions in Two-Stage Randomisation Designs in Clinical Trials With Censored Data[J].Biometrika,2006,93(1).

[2]Liang H,Härdle W,Carroll R J.Estimation in A Semiparametric Partially Linear Errors-In-Variables Model[J].The Annals of Statistics,1999,27(5).

[3]Härdle W,Liang H.Partially Linear Models[M].Springer Berlin Heidelberg,2007.

[4]Ma Y,Chiou J M,Wang N.Efficient Semiparametric Estimator For Heteroscedastic Partially Linear Models[J].Biometrika,2006,93(1).

[5]Fan J.Local Polinomial Modelling and Its Applications[M].CRC Press,1996.

[6]Tsiatis A A.Semiparametric Theory and Missing Data[M].Springer,2006.