非平稳ARMA(1，1)需求下的易腐产品供应链绩效优化研究

孙文清

（河南工程学院 管理工程学院，郑州 451191）

0 引言

在易腐产品供应链流通过程中，一旦销售商的促销方案和价格策略不合理，很容易出现易腐产品销售不出去、过期的情况，导致销售商利润减少甚至亏损。因此，研究流通过程中的易腐产品的促销及价格问题对供应链牛鞭效应和利润的影响具有重要意义。本文考虑易腐产品在非平稳的ARMA(1,1)需求条件下，引入了促销系数和价格系数两个变量，分别构建了易腐产品供应链订货模型和供应链利润函数，针对易腐产品供应链牛鞭效应、供应链利润以及牛鞭效应与利润的关系等供应链绩效问题分别进行了研究。

1 模型构建

1.1 假设条件

（1）考虑由一个供应商、一个零售商构成的二级供应链，供应链成员经营一种易腐产品，根据对下游需求的预测制订自己的订货策略；

（2）供应商向制造商采购的易腐产品单价为p，销售给零售商的单价为p1，零售商的易腐产品销售单价为p2；供应商的利润为G，零售商的利润为g；如果易腐产品在一个销售周期销售不出去，供应商蒙受的损失为H，零售商蒙受的损失为h；

（3）零售商面对的市场需求满足非平稳自回归滑动平均序列ARMA(1,1)过程，即

式（1）中，Dt——在销售周期t内易腐产品的市场需求量；

D0——已知上一年易腐产品的平均市场需求量；

α——销售商的易腐产品促销系数，为可变变量；

β——销售商的易腐产品价格系数，为可变变量；

θ——已知的需求滑动平均系数，且θ≤||1；

εt——销售周期t内市场需求随机误差项，服从正态独立同分布，均值为0、方差为σ2。

（4）针对客户需求，零售商和供应商采用相同的订货策略。

1.2 一次性订货模型构建

由于易腐产品保质期极短，只能在一个销售周期内销售，如果销售不出去，销售商则要亏掉产品的一部分本钱，因此销售商面临的是一次性订货问题。

以零售商为例。在t期末结束之前，零售商需要制订下一期的订单，由于零售商在t期并不能确定t+1期的准确市场需求量，因此，为制订合理的订单以获取最大的期望利润，零售商在t期末制订的订货决策由t+1期预测需求的条件期望和应对需求不确定性的安全库存两部分组成，其表达式为：

式（2）中，mt+1为零售商对t+1期易腐产品市场需求量预测的条件期望，为零售商的安全库存，vt+1值等于t+1期易腐产品市场需求预测的条件方差；k为表示零售商产品现货供应比的客户服务水平。

1.2.1 零售商的订货策略

零售商在t期末对t+1期的易腐产品市场需求进行预测，基于一次性订货的利润最大化原则，制订完成订单，确定订货数量qt，向供应商订货，供应商接到零售商订单后，做出快速响应，完成向零售商供货，但供货数量不多于供应商实有库存。零售商订货决策过程如下：

由式（1），零售商可对t+1期易腐产品的市场需求进行预测：

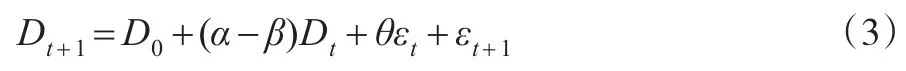
在已知条件下，由式（1）和（3），可得t+1期零售商对易腐产品市场需求预测的条件期望和条件方差，分别为：

由式（2）、（4）和（5），零售商制订出t+1期的易腐产品订单qt，并在t期末向上游供应商发出订单，该批订货由供应商根据自己实际库存数量在t期结束前完成供货：

式（6）中，k为表示零售商产品现货供应比的客户服务水平，。

1.2.2 供应商的订货策略

供应商在t期末接到零售商的订单qt，做出快速响应，一方面，根据自己实有库存，在t期结束之前完成对零售商的供货，另一方面，根据零售商订单qt信息，对零售商t+1期的订单需求量进行预测，基于利润最大化原则，制订出订单并向易腐产品制造商订货，订货量为Qt。供应商订货决策过程如下：

由式（6），供应商对下游零售商在t+1期的订货量qt+1进行预测，可得：

将式（3）代入式（7），得：

已知式（1），由式（8）可得供应商对零售商在t+1期需求预测的条件期望Mt+1和条件方差Vt+1：

由式（9）、（10），供应商制订出t期末向制造商的订货量Qt,该批订货由制造商在t+1期到来之前送达到供应商，以应对零售商在t+1期末的订货请求：

式（11）中，K为表示供应商产品现货供应比的客户服务水平。

1.3 供应链利润函数

同一批次易腐产品从供应链上游向下游销售的时间并不一致，供应商在t期末得到的、由制造商销售的订货则在t+1期末销售给零售商，而这一批零售商在t+1期得到的、由批发商交付的订货则在t+2期面向易腐产品市场，销售给消费者，如此便形成一个易腐产品销售周期。同时，面对下游客户的订单，供应商根据自己的实有库存来供货，当订单量小于实有库存量时，供给量等于订单量，当订单量大于实有库存量时，供给量等于实有库存量。

由上述分析可知，在一个易腐产品供应链的销售周期内，供应商的利润函数为：

同理，零售商的利润函数为：

由式（12）和式（13），可得一个销售周期内易腐产品供应链的总利润函数：

2 实证仿真

通过对易腐产品供应链成员的订货策略和产品销售特点，分别得到了易腐产品供应链成员的订货模型和供应链总利润的函数表达式。接下来，我们采用实证仿真方法以探究促销系数α、价格系数β对易腐产品供应链绩效的影响。

2.1 α、β与易腐产品供应链牛鞭效应

由式（6）可得零售商t期末的订货量方差：

同样，由式（11）可以得到供应商t期末的订货量方差：

易腐产品满足非平稳ARMA(1,1)过程，由式（1）知，Var(Dt)的递推公式为：

可得，t期供应商订货量和零售商订货量的方差比：

式（18）中，0≤α≤2，0≤β≤2。

借助Matlab6.5对式（18）进行仿真，见图1。

图1 促销系数α和价格系数β对供应链牛鞭效应的影响

图1反映了在区间[0,2]内α和β对易腐产品供应链牛鞭效应的交互影响。由图1可以得出如下结论：

（1）α和β对易腐产品供应链牛鞭效应的交互影响非常显著；

（2）在α和β共同影响下，易腐产品供应链牛鞭效应表现为“U”形分布；

（3）随着α和β在区间[0,2]的变化，供应链订单需求波动既存在牛鞭效应，也存在方差不变的现象，还存在反牛鞭效应。

2.2 促销系数α和价格系数β与易腐产品供应链利润

令p=4，p1=6，p2=10；考虑到农产品的市场需求呈现递增趋势，令θ=0.5；上游供应商按照实际库存量向下游客户出售产品，销售商的收益则由销售利润和因为多余库存而遭受的损失二部分构成，假设H=2，h=3；令D0=100，由式（14），随机产生52个随机扰动项ε，且ε～N(0，102)，形成50个易腐产品销售周期。根据营销实践，当市场需求量或订货量为负值时，把负值作为0处理，运用循环算法计算出易腐产品供应链总利润，据此可绘制图2。

图2 促销系数α和价格系数β对供应链利润的影响

由图2可以得出如下结论：

（1）α、β对易腐产品供应链利润的影响非常显著；

（2）随着α的增大或β的减小，供应链利润逐渐增大，当α进一步增大和β进一步减小时，供应链利润迅速增大，呈“丿”形分布。

α的增加刺激了市场需求，导致零售商和供应商的销售量和订货量的增多，使得供应链利润增加，特别地，当β=0，α=0、1、2时，易腐产品市场平均需求量分别为101、2789、1.7×1016，供应链均利润分别为 589、16709、1.05×1017。β对供应链利润起着负向影响，随着β增大，一方面，易腐产品市场需求量减少，零售商和供应商的销售量和订货量随之减少，另一方面，供应链需求波动幅度逐渐加剧，以致市场需求、订货量出现为0的情况，供应商订货量的波动幅度大于零售商订货量的波动幅度，而后者又大于易腐产品市场需求的波动幅度，当销售商库存量大于下游实际需求时，库存剩余导致大量亏损，特别地，当α=0、β=2时，市场需求、零售商和供应商的平均订货量分别为 51、53、159，其方差分别为2647、2740、25601，当α=0，β=0、0.9、2时，市场平均需求量分别为101、53、51，供应链利润分别为589、301、87。由式（1）知道，当α-β＜0时，(α-β)对Dt起着倍减作用，以致Dt出现正值、0交替出现的情况，Dt的值表现稳定；当α-β＞0时，(α-β)对Dt起着倍增作用，(α-β)越大，Dt的值迅速增大，供应链利润也随之迅速增大，特别地，当α=0、β=2时，市场需求均值为51，供应链利润为87，当α=2、β=0时，市场需求均值为1.7×1016，供应链利润为1.05×1017。

（3）供应链需求放大现象与供应链利润之间的关系。易腐产品供应链需求波动呈“U”形分布，供应链既存在方差增大现象，也存在方差不变的现象，还存在方差减小现象，|α-β|的得数越大，供应链牛鞭效应表现越剧烈；当α-β＞0且越大时，供应链利润迅速增大，当α-β＜0且越小时，供应链利润较小且较稳定，供应链利润呈“丿”形分布。因此，由本研究可知，供应链需求放大现象与利润并不相关。

3 结论

本文考虑易腐产品需求满足ARMA（1,1），引入促销系数和价格系数变量，建立了易腐产品供应链的订货模型及供应链利润函数。研究结论如下：

（1）易腐产品供应链牛鞭效应和利润受到促销系数和价格系数的共同影响，且影响显著。

（2）易腐产品供应链需求波动呈“U”形分布，既存在需求方差放大现象（牛鞭效应），也存在需求方差相等现象，还存在需求方差缩小现象（反牛鞭效应），促销系数与价格系数之间的差值越大，供应链牛鞭效应表现越剧烈。

（3）当促销系数与价格系数之间的差值为正数且越大时，供应链利润迅速增大，当促销系数与价格系数之间的差值为负数且越小时，供应链利润较小且较稳定。供应链利润呈“丿”形分布。

（4）供应链需求放大现象与利润变化情况不相关。尽管易腐产品供应链牛鞭效应和利润均受到促销系数和价格系数的交互影响，但是，就供应链需求波动而言，牛鞭效应呈“U”形分布，就供应链收益而言，供应链利润呈“丿”形分布，二者并不相关。

[1]Taesu-Cheong.Joint Inventory and Transshipment Control for Perishable Products of A Two-Period Lifetime[J].International Journal of Advanced Manufacturing Technology,2013,(66).

[2]Zeina-Sazvar,Armand B,Mohammad-Reza A J.A Replenishment Policy for Perishable Products With Non-Linear Holding Cost Under Stochastic Supply Lead Time[J].International Journal of Advanced Manufacturing Technology,2013,(64).

[3]徐娟，章德宾.生鲜农产品供应链突发事件风险的评估模型[J].统计与决策,2012,360(12).

[4]陈军,但斌.努力水平影响流通损耗的生鲜农产品订货策略[J].工业工程与管理,2010,15(2).