客观评价法中的数据差异赋权有效性及实证

苏术锋

（盐城工学院 经济与管理学院，江苏 盐城 224051）

0 引言

综合评价(comprehensive evaluation,CE)是指对被评价对象所进行的客观、公正、合理的全面评价。在综合评价中，按主客观赋权，将其方法分为两类：主观赋权法和客观赋权法。主观赋权需要客观根据指标之间相对重要程度确定权重。客观赋权法是根据评价指标数据差异程度确定权数；差异越大，赋权越大。客观赋权法有拉开档次法、均方差法、极差法、熵值法、秩和比法、变异系数法、复相关系数法、标准差法、人工神经网络法等[1～6]。

通过梳理国内外文献，发现对客观赋权综合研究法的有效性未进行深入的研究，缺乏相应的文献。因此，本文专门研究客观赋权综合评价方法的有效性问题。

1 几个重要的概念

1.1 权重定义

权重是某一指标对评价指标相对重要程度。用若干个指标x1，x2，…，xp进行综合评价时，各指标并非同等重要，故要给其赋权重。权重越大，指标越重要；反之亦然[7]。

1.2 有效性

有效性是指某一评价方法在综合评价中，达到大家公认评价方法的效果。

1.3 公理

公理1：方法A得到大家一致认可。利用方法A对事物S评价，得评价结果C，大家同样也一致认可；如果方法B对事物S评价，得评价结果D。若D=C，则方法B有效；若D≠C，则方法B无效。

2 赋权有效性验证

2.1 验证用例

表1为某一项目10个评价对象，x1和x2表示两个评价指标。用式（1）对各评价对象进行评价。

其中，wj为指标xj的权重；xij是指标值。

表1 某一评价项目值

2.2 主观赋权评价

对表1项目进行评价，主观赋权，大家一致认为x1和x2同等重要，故赋相等权重，得：

由式（1），式（2）和表1，得每个评价对象总分，见表1总分和排名。表1中的总分Z和名次P是公认评价结果。

2.3 客观赋权法验证

由于客观赋权法有多种方法，在此，只验算熵权法，均方差法和拉开档次法三种方法。

2.3.1 熵权法

（1）熵权法模型[1]

①计算第j项指标下，第i个被评对象的特征比重

②计算第j项指标的熵值

③确定权数

（2）熵权法模型求解

由熵权法，对表1数据计算可得：ws1=(0.30795,0.69205)

ws1权重总和为1，而w1权重总和为2，为了二者可比性，将ws1乘2可得ws2。

ws2与w1平均累计误差:

根据式（1），计算可得表2熵权总分S和排名S

通过上面分析可知，平均权重误差为0.2716，平均总分误差1.6848，平均排名误差0.3461202。

2.3.2 拉开档次法

（1）拉开档次法模型[1]

（2）拉开档次法求解

由拉开档次法，用MATLAB7.0求H=ATA，得H的值。用MATLAB7.0，求H的特征向量矩阵V及特征值矩阵D。[V,D]=eig(H)，其中：V为特征向量矩阵;D特征值矩阵。取D中最大特征值：λmax=6.5255；其对应特征向量Vmax权重：

wl0=(0.62931,0.77716)T。对wl0归一化得：

wl1=(0.44744,0.55256)T

为了与w1对比，将wl1乘2得wl2：

计算wl2w1与，平均累计误差

使用wl2和表1中指标，按式（1）式计算，可得表2拉开档次总分L，拉开档次名次L。

通过上面分析可知，拉开档次法平均权重误差0.074331，平均总分误差0.46109，平均排名误差0.2828427。

2.3.3 均方差法

（1）均方差法模型[1]

（2）均方差法求解

由均方差法，对表1数据计算可得权重：

为了与w1对比，将wf1乘2得wf2：

计算wf2与w1平均累计误差:

使用wf2和表1中指标，按式（1）式计算，可得表2均方差总分F，均方差名次F。

通过上面分析可知，平均权重误差0.25911，平均总分误差1.5977，平均排名误差0.2828427。

表2 三种评价方法与主观赋权法比较

2.4 三种方法相对有效性分析

虽然客观赋权法与主观赋权法存在不一致，但各种客观赋权法与主观赋权法还可以比较相对有效性。比较原则：名次误差最小为优；名次误差相同，总分误差小，为最优；如果名次和总分误差相同，则权数误差小，为最优。由表2中的三种方法名次，比较可得表3。

表3 三种方法相对有效性排名

三种方法相对有效性：拉开档次法＞均方差法＞熵权法。

2.5 三种方法绝对有效性分析

表1中排名P，是主观赋权评价的结果，是大家一致公认的。但用熵权法拉开档次法和均方差法对表1中的学生成绩进行评价，其结果均与大家公认的排名P不一致。根据公理1，熵权法、拉开档次法和均方差三种评价法均无效。

3 进一步分析与讨论

3.1 客观赋权与主观赋权评价结果差异性分析

这里只对熵权法进行分析，其它方法类似。

用熵权法，x1权重0.6159，x2权重1.384。就表4中S4与S5而言，S5的x2的100与S4的x1的100分是不等价的；S5的x2的100计算到总分中的分值是100×1.384=138.4,而S4的x1的100计算到总分中的分值是100×0.6159=61.59，从而造成了S5(总分177)排到S4(总分178)前面的不合理结果。这样的评价结果与评价者主观愿望不一致，从而使评价者不能接受[1]。其它的评价对象S6、S7、S8、S9排名问题基本上与S4和S5一样。所以客观赋权法与主观评价法名次不一致的原因是客观赋权数据差异赋权造成的。

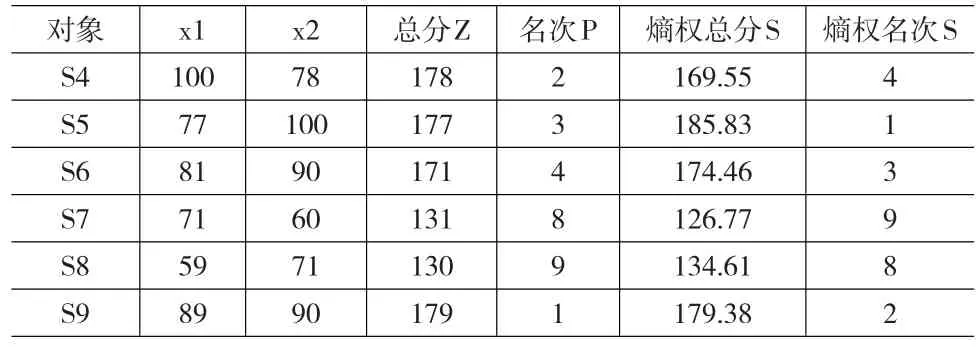
表4 熵权法名次差异情况

3.2 客观赋权理论分析

客观赋权法是根据数据差异确定指标权重的。数据差异越大，指标权数就越大。但数据差异程度大小并不能反映指标的重要程度。二者不是一个概念，强行将数据差异程度等同于指标的重要程度是不正确的，所以客观赋权通过数据差异程度来确定指标的权重，从理论上讲，是不正确的。

4 结论

第一，权重是指标的重要程度的表述，确定权重的基本方法就是比较指标之间的重要程度，它与样本数据无关。没有评价样本数据之前，只要确定好各指标，就可以确定出各指标的权重。而数据差异的客观赋权，即使有了各指标体系，在没有样本的情况下，无法确定指标的权重。第二，数据差异的客观赋权，相同的指标体系，换了一组数据样本，其指标权重就会发生变化，这是非常不合理的。第三，数据差异来确定权重，与权重的定义相悖。数据差异说明不了指标是否重要。第四，通过主观赋权一个简单实例，就会发现数据差异的客观赋权法存在问题。第五，客观赋权缺乏理论支持，故它不是学术界以后的研究方向。总之，数据差异的客观赋权缺乏理论根据，是一种存在瑕疵、有效性不稳定的方法。

[1]郭亚军.综合评价理论、方法及拓展[M].北京：科学出版社,2012.

[2]胡斌，章仁俊.基于秩和比法的区域科技发展水平比较研究[J].工业技术经济,2004,(12).

[3]孙凯,鞠晓峰.基于变异系数法的企业孵化器运行绩效评价[J].哈尔滨理工大学学报,2007,(6).

[4]梅国平.基于复相关系数法的公司绩效评价实证研究[J].黑龙江水利科技,2004,(1).

[5]张咏祀.标准差法在森林立地质量评价中的应用[J].西华师范大学学报,2008,(12).

[6]朱大奇.人工神经网络研究现状及其展望[J].江南大学学报,2004,(2).

[7]胡永宏，贺思辉.综合评价方法[M].北京：科学出版社,2000.