稳定分布条件下的动态风险度量模型

武 东，李 琼，刘爱国

（1.安徽农业大学 理学院，合肥 230036；2.安徽商职业学院 电子信息系，合肥 230022）

0 引言

金融时间序列主要研究资产价值随时间变化的理论与实践。最为常见的金融时间序列是股票序列，其主要特征有收益率序列非平稳性、弱相关性、波动性聚类、厚尾性和杠杆效应等诸多特征。为了刻画金融时间序列的这些特征，常采用GARCH族模型[1]进行拟合。1982年，Engle首创了自回归条件异方差模型[2](简称ARCH模型)，该条件方差模型是过去新息平方的函数，它运用ARCH模型并结合AR模型成功预测了英国通货膨胀问题。1986年，Bollerslev推广了ARCH模型，将过去的条件方差引入条件方差模型得到GARCH模型[3]，该模型能较好地计算股票收益率序列的波动率。然而，ARCH模型和GARCH模型的条件方差均为过去新息平方的函数,因此价格的升降变化对条件方差的影响是对称的。但实践中，人们发现当好消息出现时，证券市场波动变化不大，而坏消息出现时，证券市场波动变化增大。通常，EGARCH模型和GJR-GARC H模型等非对称GARCH模型均能刻画新息的不对称影响。

近来，文献[4]推广了GARCH模型和EGARCH模型得到了基于稳定分布的PARCH模型和EPGARCH模型，并对沪深股票市场进行了实证研究。EPGARCH-S模型能刻画金融时间序列的厚尾性、波动聚类性和杠杆效应等特征。在证券市场的实证分析中，首先对沪深港美股票指数的对数收益率序列进行了描述性分析，得出它们均具有高峰厚尾特性和GARCH效应。然后，利用EPGARCH-S模型和EGARCH-t模型对沪深指数的对数收益率序列计算了风险值(VaR[5])。统计表明，基于EPGARCH-S模型的VaR能较好地评价金融风险。

1 模型

Mandelbrot(1963)[6]和Fama(1965)[7]指出股票价格的对数收益率序列呈非正态性，建议使用稳定分布拟合股票价格的对数收益率。众所周知，稳定分布族是正态分布的一种推广，但稳定分布没有解析的密度函数形式只能用它的特征函数进行描述。下面给出一种较为常用的稳定分布的特征函数的定义[8]。

定义1若随机变量X的特征函数可表示为

则称随机变量X服从稳定分布，记为S(α，β，γ，δ)，如果参数γ=1，δ=0，则称为标准稳定分布,并简记为S(α，β)。这里α表示尾部特征参数，主要反映分布尾部的厚薄程度；而β表示偏性参数，β＞0表示分布密度曲线是左偏的，β＜0表示分布密度曲线是右偏的，当β=0时,这时分布是对称的。

假设证券价格的日收益率的条件均值方程为

其中新息zt的分布是零均值单位方差的标准化分布，由于EGARCH模型能较好地捕获金融时间序列的高峰厚尾特性和杠杆效应等，文献[4]进一步推广了EGARC H模型得到了EPGARCH模型，本文的条件方差函数采用EPGARCH模型，其表述形式为

若条件方差模型中的新息分布为稳定分布，从而得到基于稳定分布的EPGARCH模型，记为EPGARCH-S模型。当d=2时，则退化为EGARCH模型，若取新息分布为t分布，则能得到基于t分布的EGARCH模型，简记为EGARCH-t模型。下面利用这两个模型对沪深证券市场的收益率序列进行统计建模并考查二者在VaR计算方面的有效性。

2 证券市场的实证分析

2.1 证券市场的特征分析

现在将上证综合指数(000001)、深证成指(399001)、创业板指(399006)和创业300(399012)的日收盘价格作为研究对象。时间区间为2010年6月1日到2014年4月30日。这是因为2008～2009年是全球金融风暴，故选择的时间起点为2010年，这样可以减少在此之前股票价格大幅度波动对数据质量的影响。收益率选取日收盘价格的对数收益率，即pt为第t天的收盘价格，则第t天的收益率的公式为rt=100(lnpt-lnpt-1)。

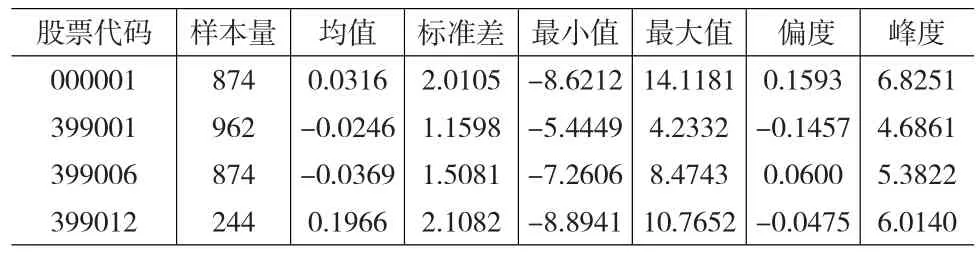
表1 沪深指数日对数收益率的描述统计

表1列举了沪深港美股指收益率序列的描述性统计指标。四只股票指数的日对数收益率的峰度均大于3，说明其具有高峰厚尾特性。下面利用EGARCH类模型对上述股票指数的收益率序列进行建模，表2列举了股票指数的EGARCH类模型的参数估计结果。在EGARCH-t模型的参数估计中，α表示t分布的自由度，模型参数估计的方法采用了约束条件下的非线性优化算法[4]。从表2中的α值可以看出,股票的收益率序列都具有高峰厚尾特性,因为EPGARCH-S模型中的参数α是刻画尾部特征的，β是偏性参数。说明EPGARCH-S模型可以刻画股票市场的非对称性(杠杆效应)。

表2 沪深指数日对数收益率的EGARCH类模型的参数估计

2.2 风险度量的计算原理

定义2设随机变量Z表示投资一定数额的资产W后，在未来某一持有期T内的损益，则称满足P{Z＜-VaR}=α的正数VaR为该投资组合在未来持有期T内置信水平为1-α的风险值。

假设该投资组合在[0 ，T]时期内的收益率X=Z/W的分布函数为F(x)，且该投资组合的收益率分布的下侧α分位数为xα=sup{x|P{X≤x} ≤α} ，则VaR(Z)=-xαW， 对于收益率序列{rt},可以得到VaR(rt)的计算公式为

2.3 EGARCH类模型在风险值计算中的比较分析

表3和表4给出利用EGARCH类模型计算得到股票收益率的风险值模型结果。下面利用Kupiec提出的似然比检验法[9]验证EGARCH类模型的有效性。在Kupiec假设检验中，若N为检验样本中损失高于VaR值的次数，n为样本量。假设损失超出VaR值的次数服从二项分布，即N～B(n，1-α)，其中α为所用模型采用的置信水平，因此失效率f=N/T应等于p。Kupiec假设检验的原假设为H0:f=p，相应的似然比统计量为

由表3和表4可以得到如下结论：第一，从Kupiec检验的P值可见，在显著性水平0.05，0.01下，EPGARCH-S模型基本上都是有效的，只有当显著性水平为0.05时，创业板指的VaR模型失效，因为其P值小于给定显著性水平，而基于EGARCH-t模型的VaR模型都是失效的，因为所有P值均很小，说明EPGARCH-S模型能较好地刻画风险，而EGARCH-t模型拟合效果欠佳；第二，从失效天数、失效比率可以发现，基于EEPGARCH-S模型计算得到的失效比率接近于显著性水平，而基于GARCH-t模型计算的失效比率偏离显著性水平较大；第三，从VaR均值比较可见，基于EPGARCH-S模型的VaR均值要略低于基于EGARCH-t模型的VaR均值，说明基于EGARCH-t模型的VaR值过于保守且不够准确；第四，由VaR均值可以得到结论：在一定显著性水平下，创业板指(399006)和创业300(399012)两只创业股的风险值要大于两只综合指数股，说明其风险更高，投资时须谨慎。

表3 基于EGARCH类模型的VaR计算(α=0.05)

表4 基于EGARCH类模型的VaR计算(α=0.01)

通过上面的比较分析,可以得出结论：一方面，由于稳定分布相对于t分布更具有灵活多变的特征，而稳定分布能较为准确地刻画金融时间序列的尾部特征；另一方面，EPGARCH模型比EGARCH模型增加了一个未知参数，形式更加灵活，对收益序列的波动率的捕获能力更强。综上所言，EPGARCH-S模型对我国股票市场的对数收益率波动率的拟合准确度较高,能较好地描述证券市场的对数收益率的“易变性聚类”现象和“高峰厚尾”特性。

3 结论

EPGARCH-S模型融合了稳定分布和EPGARCH模型二者的优点，从而能很好地刻画证券市场对数收益率序列的诸多特征,如高峰厚尾,波动聚集性,非对称性等。故本文采用了EPGARCH-S模型对我国证券市场的对数收益率序列进行了风险值计算，从Kupiec检验结果来看，其精度高于传统的EGARCH-t模型。统计表明，EPGARCH-S模型能很好地计算和评估股票市场的风险价值。

[1]张世英,樊智,协整理论与波动模型:金融时间序列分析及应用[M],北京:清华大学出版社，2004.

[2]Engle R F.Autoregressive Conditional Heteroskedasticity with Estimation of The Variance of United Kingdom Inflation[J].Econometrica,1982,(50).

[3]Bollerslev T.Generalized Autoregressive Conditional Heteroskedasticity[J].Journal of Econometrics,1986,(31).

[4]武东,汤银才,基于稳定分布的EPGARCH模型[J].工程数学学报，2008,25(1).

[5]Jorison P.Value at Risk:The New Benchmark for Controlling Market Risk[M].New York:McGraw-Hill Companies,1997.

[6]Mandelbrot,B.The Variation of Certain Speculation Prices[J].Journal of Business,1963,(26).

[7]Fama E F.The Behavier of Stock Prices[J].Journal of The Business,1965,(38).

[8]武东,汤银才.稳定分布及其在金融中的应用[J].应用概率统计，2007,23(4).

[9]Kupiec P.Techniques for Verifying The Accuracy of Risk Measurement Models[J].Journal of Derivatives,1995,(2).