基于抗侧刚度的三面广告牌格构式立柱设计优化及缩尺模型试验

李瑞鸽 杨国立 张 恒 姜雨芃 张 宇 王子川

(台州学院建筑工程学院,台州 318000)

基于抗侧刚度的三面广告牌格构式立柱设计优化及缩尺模型试验

李瑞鸽*杨国立 张 恒 姜雨芃 张 宇 王子川

(台州学院建筑工程学院,台州 318000)

高耸广告牌格构式立柱的风荷载和抗侧刚度是设计时要考虑的主要问题。分析了格构式立柱截面宽度与柱高的比值对柔度系数的影响、腹杆截面面积与格构式弦杆截面面积比值对柔度系数的影响、立柱截面形状对柔度系数的影响等。根据优化结果，选择了适合的格构式立柱，使结构在材料用量相同的情况下，空间抗侧刚度达到最大。最后制作了缩尺模型在一定风速下进行了荷载试验，试验结果表明,提出的方法是合理可行的，能够为同类型结构的设计提供参考。

广告牌， 柔度系数， 格构式立柱， 试验

1 引 言

高耸的落地式三面广告牌，由于其广告面大，高度高，宣传效果良好，被广泛地应用于城市闹市区、高速公路旁等位置，为商业及经济的发展起到不可磨灭的促进作用。这种广告牌一般竖向荷载很小，而水平荷载很大，要求结构具有良好的强度、刚度和稳定性。从实际工程来看可有以下方案实现：

(1)大直径钢管柱：施工方便，计算理论成熟，但是钢管直径过大，存在钢管壁局部稳定问题。

(2)钢管混凝土柱：相同条件下，柱截面抗弯刚度大，钢管局部稳定有保障，但是，施工工序及复杂程度增加[1]。

(3)格构式钢结构立柱：抗侧能力强，钢材用量少，但是设计、计算复杂，结构截面形状、尺寸等参数的选择需要优化[2]。

根据以上分析，格构式钢结构立柱具有经济效益好、抗侧刚度大等优点，因此本文就格构式立柱截面形式、弦杆和腹杆截面面积等设计参数的选择方面进行分析和优化，为海边、山谷等风荷载较大地方的大型广告牌格构式立柱的设计提供参考。

2 基于抗侧刚度的立柱形式选择

钢结构的特点是抗压能力和抗拉能力强，但是刚度一般都比较小，所以钢结构设计中应该着重考虑的问题是失稳和侧移刚度。由于大型广告牌的竖向荷载一般都很小，水平风荷载很大，因此必须选择抗侧刚度大的立柱，满足其侧移的限值，按照文献[3]的规定，户外广告牌结构受风荷载作用时，结构顶点最大水平位移不应超过高度的1/100。广告牌立柱的侧移变形包括弯曲变形和剪切变形。由于广告牌的立柱不像建筑结构的柱子那样，有楼盖或者屋盖强有力的约束，因此不会产生较大的剪切变形，所以其剪切变形可以忽略不计。格构式立柱的弯曲侧移与立柱的整体刚度成反比，因此减小立柱的侧移，必须使其整体刚度尽量大，即结构的柔度尽量小。

格构式立柱广告牌结构属于悬臂结构，如图1所示。在水平力作用下，结构顶端的位移与结构的抗侧刚度有关。工程上常用的格构式立柱腹杆布置形式如图2所示。用结构力学单位力法可以计算得到其对应柔度，根据结构的柔度与刚度成反比的关系，可以知道结构的刚度大小[4]。

图1 水平荷载下结构受力示意图

图2 常用的腹杆布置形式

表1 常见腹杆的柔度系数

Table 1 Flexibility factor of common web

类型柔度系数δ/(N·m-1)Aδ=2H331+18n2()λ1+Hλ2Bδ=2H331+12n2()λ1+Hλ2Cδ=2H331+12n2()λ1+H(λ2+λ3)Dδ=2H331-32n+12n2()λ1+H2(λ1+λ2)Eδ=2H331-14n2()λ1+H2λ2Fδ=2H331-14n2()λ1+H2λ3

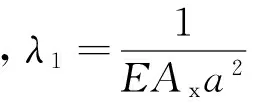
从表1中可以看出，弦杆的截面尺寸对结构的刚度贡献较大，因此一般采用较大的弦杆面积，而横腹杆和斜腹杆的主要作用是为了减小弦杆的计算长度，可以采用较小的截面尺寸。

在这6种腹杆布置形式中挑选柔度系数小并且节省材料的布置方式，D型和E型的布置方式较好，如果同时从便于加工等角度考虑，E型所示的方式更优。

3 立柱杆件截面的优化

根据表1中类型E的柔度计算公式，采用Matlab编程计算a值(a为立柱截面的高宽比)的变化对柔度的影响。计算结果如图3所示，其中，图3(a)为弦杆截面面积为27 mm2时，腹杆截面面积为弦杆截面面积的1/3时(即9 mm2)，柔度系数与a的关系；图3(b)为弦杆截面面积为9 mm2，腹杆截面面积为4 mm2时，柔度系数与a的关系曲线。由图可知，当a=0.23～0.24时，格构式立柱的柔度取得最小值。

图3 a值与柔度系数的关系

根据图3可知，柔度系数随a值的变化趋势基本相同，其关系曲线都近似为抛物形状。杆件截面尺寸对柔度系数随a值的变化趋势影响不大。a值大约为0.24时效果最佳。

为研究弦杆截面面积与腹杆截面面积对结构抗侧刚度的影响，使整体结构的质量尽量轻，同时将材料质量利用效率提高，固定弦杆截面面积(12mm2)，改变腹杆的截面尺寸，编写Matlab程序分析了腹杆截面面积与弦杆截面面积的比值和模型质量的关系(图4)。由图可知，弦杆截面面积一定时，腹杆和弦杆面积比值与模型质量近似呈线性关系。同时还分析了腹杆截面面积与弦杆截面面积的比值和柔度系数间的关系(图5)。由图5可知，截面面积比值大概在0.3～0.5时，效率最高，该系数大于0.5以后，柔度系数的降低幅度明显变小。

图4 弦杆、腹杆截面积的比值和模型质量关系

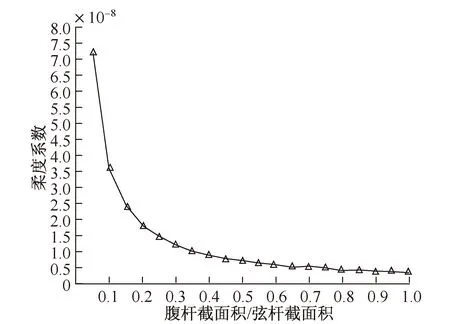
图5 腹杆与弦杆截面积的比值和柔度系数关系

现取腹杆截面面积与弦杆截面面积比值为1/3，采用Matlab编程计算并绘制图形表达弦杆截面面积与柔度系数的关系(图6)，以及弦杆截面尺寸与模型质量的关系(图7)。由图可知，柔度系数与弦杆截面面积近似呈线性关系，模型质量与弦杆截面面积成线性关系。因此在选用截面尺寸时，根据荷载的大小确定即可。

模型广告牌为三面的，水平投影形状为边长为800 mm的等边三角形，所以，立柱水平投影形状可以采用三角形或者四边形。当采用等边三角形时，抗侧刚度最小为2sin(π/3)K，质量增加较少;采用四边形时，抗侧刚度为2K，但是质量增加较多。选择a/H值为0.24，腹杆截面面积为弦杆截面面积的1/3，通过改变弦杆和腹杆的截面面积，计算三角形截面立柱和正方形截面立柱的质量和柔度系数，编写程序分别对这两种截面形状进行分析，结果如图8所示。由图可知，在同样质量的情况下，正三角形截面形状的柔度系数小于正方形截面形状的柔度系数，尤其是质量较轻的情况，柔度系数的大小差别更加明显，因此选择柔度系数小的正三角形截面形状更好。

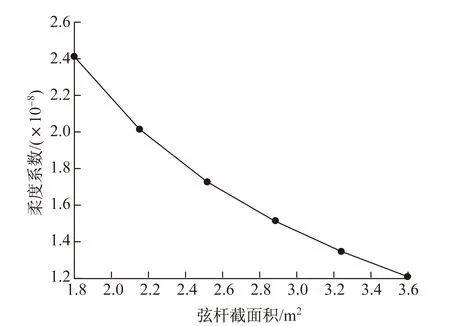
图6 弦杆截面积与柔度系数关系

图7 弦杆截面积与模型质量关系

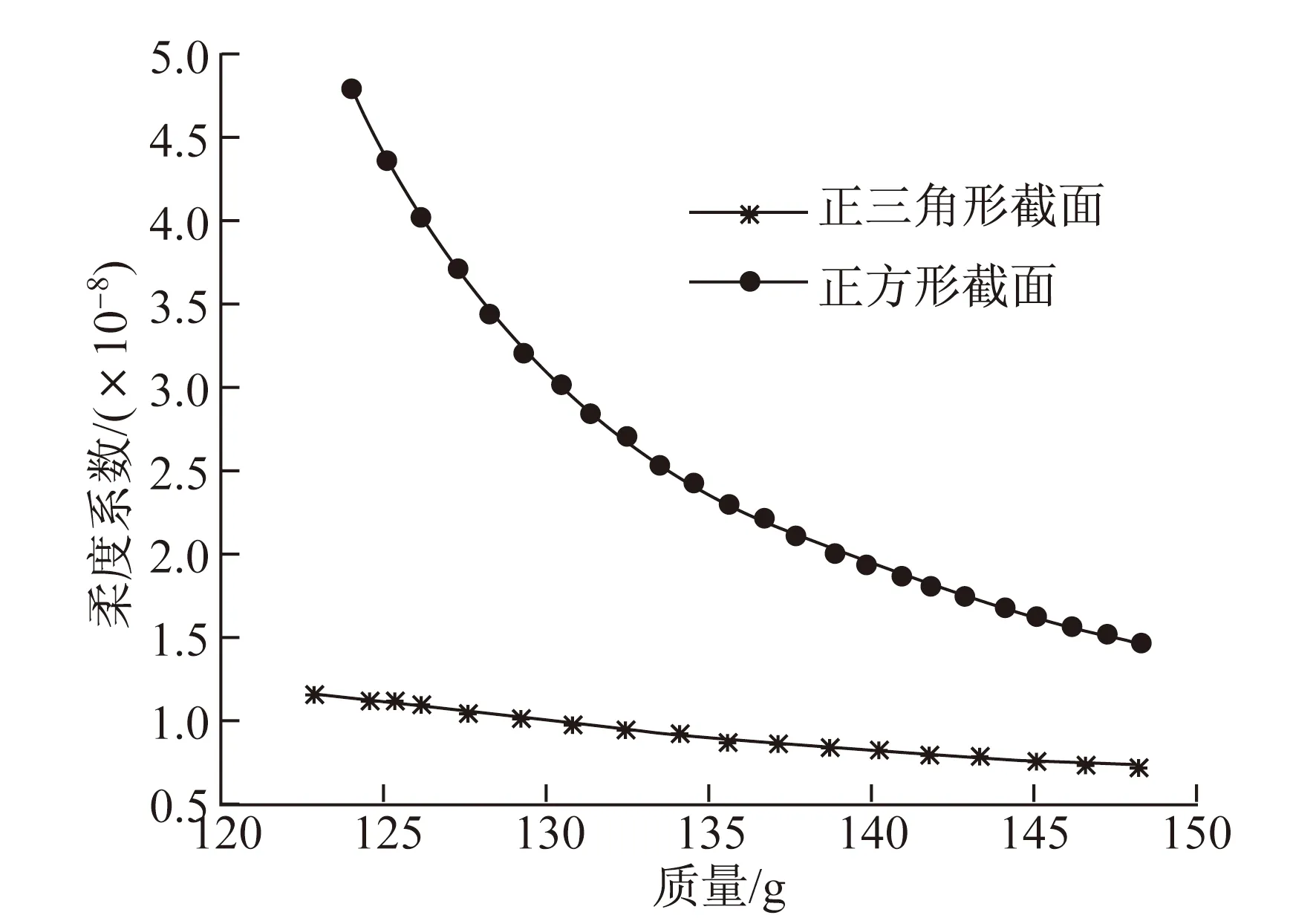
图8 立柱截面形状与模型质量及柔度系数的关系

4 模型加载试验

巨型广告牌格构式立柱体积较大，做足尺模型试验几乎不能实现[5]，为研究立柱截面形式、立柱弦杆和腹杆截面面积关系、立柱截面尺寸与高度关系对立柱抗侧刚度的影响，特制作了缩尺模型进行分析，并进行了抗风试验。缩尺模型格构式立柱总高度为1 m，广告面高度为200 mm，广告牌平面投影800 mm×800 mm。缩尺模型采用集成竹材料，其力学参数见表2。

表2 缩尺模型试验材料力学参数

Table 2 Parameters of model material

根据设计尺寸制作了广告牌模型，并且利用风机进行加载试验。缩尺模型及加载试验装置如图9所示，其中弦杆和腹杆截面面积分别为12 mm2和4 mm2，总重量为51 g。调节鼓风机与模型间的距离控制模型所承受的风力。在承受12m/s的风速时(相当于6级强风)，顶端侧移为76 mm。集成竹的弹性模量为10 GPa，钢材的弹性模量为200 GPa，因此模型的弹性模量的相似常数为1/20,取应力的相似常数为1，则应变的相似常数为20。根据《户外广告设施钢结构技术规程》[3](CECS148：2003)第5.4.1条的规定，在风荷载作用下，落地式广告牌钢结构顶点的水平位移不应超过该点离地高度的1/100。该结构在6级强风下，原型结构的顶端侧移与高度的比值为0.38/100,满足规范要求。加载试验如图10所示。在试验过程中观察到：虽然模型的顶端侧移不大，但是截面尺寸小的斜腹杆和水平腹杆受压屈曲，变形严重，因此在极端条件下，还应考虑腹杆的承载力。

图9 缩尺模型及加载装置

图10 加载试验

5 结 语

本文探讨了承受水平荷载较大的高耸落地式广告牌格构式立柱的设计，着重从格构式立柱抗侧刚度出发，分析了格构式立柱的截面宽度和立柱总高度的关系、不同截面形状的抗侧能力、弦杆和腹杆的截面面积关系等。分析表明，格构式弦杆的间距为立柱总高的0.23～0.24倍时，抗侧效果最好；对于三面广告牌，三角形的格构柱截面在材料重量相等的情况下，抗侧效率更高；弦杆和腹杆的截面面积比值在0.3～0.5的时候最好。同时采用与钢材相似的竹材制作了缩尺模型，在没有风洞实验室的情况下，利用鼓风机加载，对缩尺模型进行了风载试验，试验表明，采用以上设计参数设计的广告牌立柱模型具有更好的抗侧刚度。本文的分析方法和分析结果可以为巨型落地式广告牌格构式钢结构立柱的设计提供理论参考和设计依据。广告牌的立柱除了要具有良好的抗侧刚度外，还应该具有良好的稳定性和抗扭刚度，因此在设计高耸广告牌格构式立柱时，还要做更多的分析和优化计算。

[ 1 ] 王华琪,丁洁民,何志军.防屈曲支撑的应用与设计[J].结构工程师,2008, 23(4):6-11.

Wang Huaqi, Ding Jiemin, He Zhijun. The application and design of buckling-restrained braces[J]. Structural Engineers, 2008, 23(4):6-11.(in Chinese)

[ 2 ] 宫海,李国强.多高层建筑钢结构实用优化方法研究[J].结构工程师,2006, 22(1):1-5.

Gong Hai, Li Guoqiang. Practical optimization method for structural design of multi and tall steel buildings[J]. Structural Engineers, 2006, 22(1):1-5.(in Chinese)

[ 3 ] 中国工程建设标准化协会高耸构筑物委员会.CECS148：2003户外广告设施钢结构技术规程[S].北京: 中国计划出版社，2003.

China Association for Engineering Construction Standardization Committees Towering Structures. CECS148:2003 Technical specification for steel outdoor advertising facilities[S]. Beijing: Planning Press, 2003.(in Chinese)

[ 4 ] 陆念力,王佳,兰朋.格构式构件整体稳定性分析的等效惯性矩法[J].建筑机械,2008,(08):79-84.

Lu Nianli, Wang Jia, Lan Peng. Equivalent inertia moment method to the overall stability analyse of lattice type beam[J]. Construction Machinery,2008,(08):79-84.(in Chinese)

[ 5 ] 刘明.土木工程结构试验与检测[M].北京:高等教育出版社,2008.

Liu Ming. Test and inspection of civil engineering structures [M]. Beijing: Higher Education Press, 2008.(in Chinese)

Design Optimization and Scaled Model Tests of the Three Sides Billboard Lattice Column Basal on Lateral Stiffness

LI Ruige*YANG Guoli ZHANG Heng JIANG Yupeng ZHANG Yu WANG Zichuan

(School of Civil Engineenig & Architecture, Taizhou University, Taizhou 31800, China)

The wind loads and lateral stiffness of towering billboards lattice columns were major factors that should be considered in design. Several factors affecting the flexibility factor were analyzed in this paper, that is: the ratio of column cross-section width and height impact on the flexibility factor, area ratio of the web and chord cross-sectional impact on the flexibility factor, and the column cross-sectional shape impact on the flexibility coefficient and so on. A suitable lattice column was chosen based on the optimization results, stiffness was maximized by the same amount of structural material. Finally, a test by scaled model was done, the test results show that the proposed method is reasonable and feasible, and it can provide a reference for the same type of structural design.

billboard, flexibility coefficient, lattice column, test

2013-12-06

*联系作者，Email:lrg@tzc.edu.cn