预制组合箱梁节段混凝土收缩自应力分析

曾明根 陈文超 苏庆田

(1. 同济大学建筑设计研究院，上海 20092; 2. 同济大学桥梁工程系，上海 200092)

预制组合箱梁节段混凝土收缩自应力分析

曾明根1陈文超2,*苏庆田2

(1. 同济大学建筑设计研究院，上海 20092; 2. 同济大学桥梁工程系，上海 200092)

为了解预制组合箱梁节段中混凝土收缩对梁体各个部位受力性能产生的影响，结合一具体工程建立了组合箱梁的板壳—实体有限元混合模型，详细计算分析了预制组合梁节段在混凝土收缩作用下的受力情况，得到在混凝土收缩效应作用下组合箱梁中混凝土产生一定程度的拉应力，钢梁产生一定程度的压应力，应力分布规律复杂。进一步比较分析了混凝土板厚、钢梁底板厚度、预制混凝土桥面板宽度、预制节段长度等参数变化下混凝土收缩对组合梁桥受力的影响，得到预制节段长度对混凝土纵桥向应力影响显著，在斜拉桥中减少组合梁纵桥向节段长度能够有效减少混凝土的纵桥向收缩拉应力。

预制节段, 组合梁, 收缩, 有限元

1 引 言

组合梁相比混凝土梁具有结构轻巧、施工便捷、整体性能好、跨越能力强的优势；与钢梁相比具有造价低、体系刚度大、养护费用低等方面的显著优点，同时因桥面为混凝土结构，可克服钢桥面铺装的耐久性问题[1-2]。为此，组合梁斜拉桥以其组合梁的经济性、行车环境及斜拉桥良好的跨越能力在大跨径(300～600 m)斜拉桥中占据一定的优势[3-4]。

混凝土的自身收缩会在钢-混凝土组合梁中产生应力重分布效应[5-6]。在大跨度组合梁斜拉桥中为了降低混凝土收缩产生的应力效应，一般采用节段预制、拼装施工方法[7-10]；目前的大跨度组合梁斜拉桥主梁一般采用开口形式的钢主梁，通过横梁和小纵梁与混凝土桥面板相连。这种组合梁的混凝土桥面板在纵桥向和横桥向分块，混凝土桥面板根据桥面系梁格的尺寸预制而成。这种组合梁中混凝土收缩效应的影响已有相关的研究[9,10]。

浙江省台州市椒江二桥采用了组合梁形式斜拉桥，其组合梁截面为分离式双箱组合梁，与常规的斜拉桥组合梁不同，为了降低组合梁混凝土收缩效应在组合梁中产生的应力，采用了大节段预制方法，而且混凝土预制时在横桥向为一完整体，没有湿接缝。这种组合梁的预制方法与传统的斜拉桥组合梁预制工艺不同，且其在混凝土收缩作用下的效应具体如何也尚未见到有关分析。为此本文结合椒江二桥，对组合梁节段在预制期间混凝土收缩影响进行有限元计算分析，并通过参数对比分析，提出减小预制组合梁节段收缩自应力的措施。

2 工程概况

椒江二桥位于浙江省台州市，主桥为双塔双索面斜拉桥，整体式五跨连续漂浮体系，跨径为(70+140+480+140+70) m，如图1所示。斜拉索标准索距为9 m，边跨尾索区索距为6 m。主梁采用分离式半封闭双箱组合梁，如图2所示，中心线处内轮廓梁高3.5 m，主梁全宽为42.584 m(含风嘴)，不含风嘴组合梁全宽34.7 m。组合梁中混凝土桥面板厚度除了在加腋处及尾索区压重段为400 mm，其余均为260 mm。

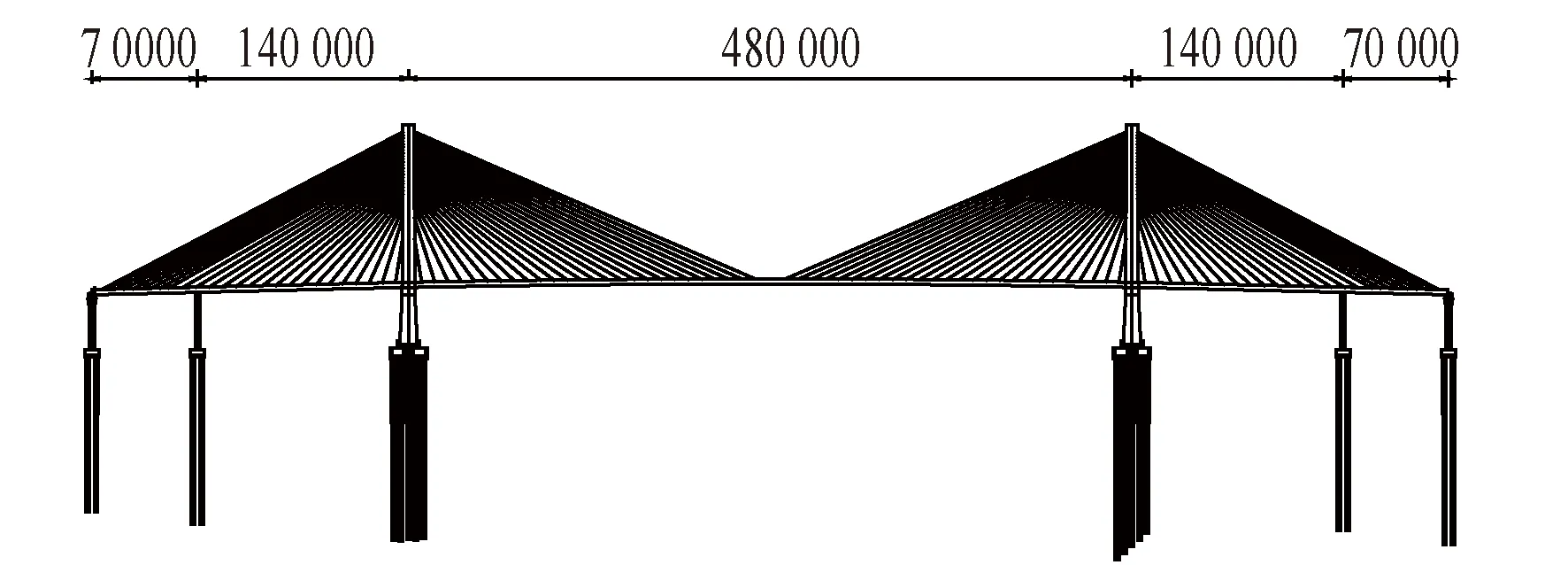
图1 主桥纵向布置图(单位：mm)

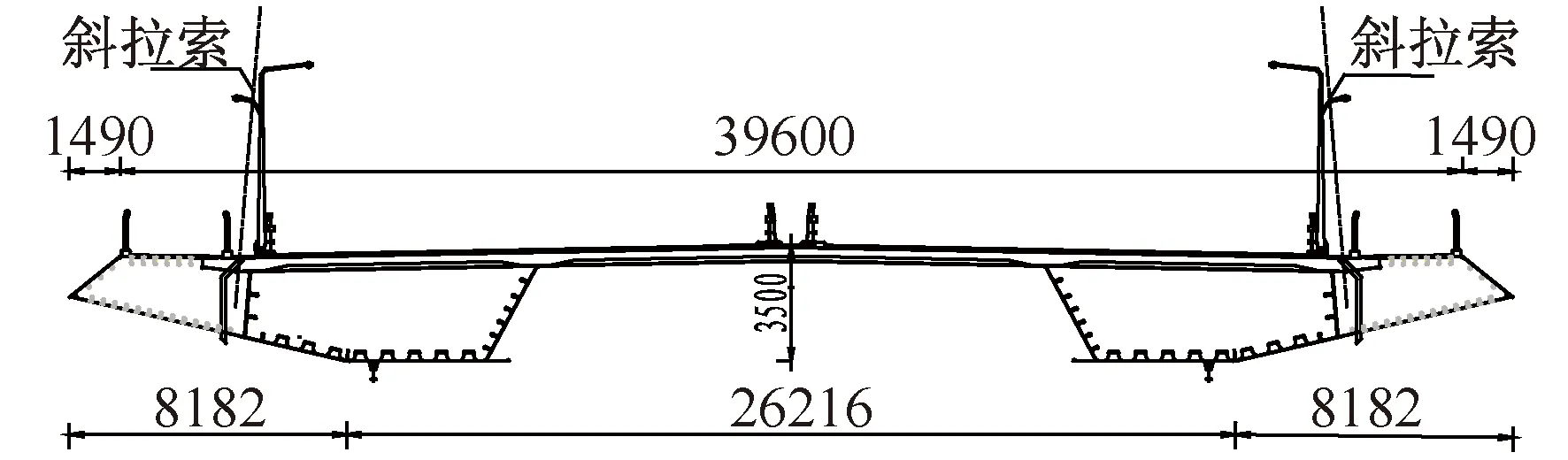
图2 横断面标准图(单位：mm)

椒江二桥采用预制节段拼装法施工，在预制场标准节段长度为9 m，每个节段在预制场先浇筑8 m范围的混凝土，两端各预留0.5 m的湿接缝；预制节段在平均相对湿度75%条件下养护6个月(180天)后，运至桥位，通过吊装、钢梁拼接、现浇混凝土湿接缝形成全桥。

3 有限元模型

选取实桥中标准节段建立板壳实体有限元模型，如图3所示。该节段混凝土桥面板在加腋处厚400 mm，其余均为260 mm，钢箱梁边腹板厚30 mm，中腹板厚16 mm，U肋板厚8 mm，钢箱上缘板厚24 mm，底板板厚20 mm。混凝土采用实体单元模拟，钢梁采用板壳单元模拟，混凝土和钢板上翼缘之间的焊钉采用接触单元模拟，剪力钉剪切刚度参考实验值[3]采用4.13×105kN/m，预制梁段采用C60混凝土，混凝土容重为26 kN/m3，弹性模量为3.6×104MPa，泊松比为0.1667，线性膨胀系数为1.0×10-5。钢材采用了Q345qd，容重为78.5 kN/m3，弹性模量2.06×105，泊松比为0.3，线膨胀系数为1.2×10-5。

预制存放过程中组合箱梁节段在钢底板与内腹板交界处和钢底板与斜底板的交界处均匀布置了约束，节段两端为自由。为模拟组合箱梁节段在预制过程中的实际情况，在模型每条交界边上沿梁纵向均匀布置了5处约束点，其中只对一点进行了竖向、纵向、横向约束，其余各点只进行竖向约束，模型的约束情况见图3。有限元模型的约束条件能够确保组合箱梁节段在预制存放过程中混凝土的自由收缩，同时又与实际情况相符。

图3 预制节段有限元模型

组合箱梁节段实际存放180天，预制节段存放过程中考虑混凝土的收缩，收缩应变根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)[11]进行计算，收缩绝对龄期假设为7天，按照混凝土养护180天计算混凝土的收缩应变，并换算成等效温度荷载，在有限元软件ANSYS中通过温度荷载实现。

4 计算结果分析

4.1 预制组合梁节段收缩自应力分布规律

图4为混凝土桥面板顺桥向应力分布图。可以看出，混凝土桥面板上表面顺桥向应力在-0.4～0.4 MPa，混凝土桥面板下表面顺桥向应力在-0.3～1.0 MPa。在腹板位置处的上表面，混凝土顺桥向压应力水平较小，这是因为相比横隔板翼缘，主梁钢翼缘是阻碍混凝土纵向收缩的主要因素，此处钢梁与混凝土交界面上产生较大约束剪应力，从桥面板上表面到下表面，桥面板的顺桥向压应力逐渐减小，混凝土板下表面出现顺桥向拉应力。混凝土加腋处大部分拉应力在1.0 MPa左右，但是在加腋端部，由于截面突变出现了拉应力集中。

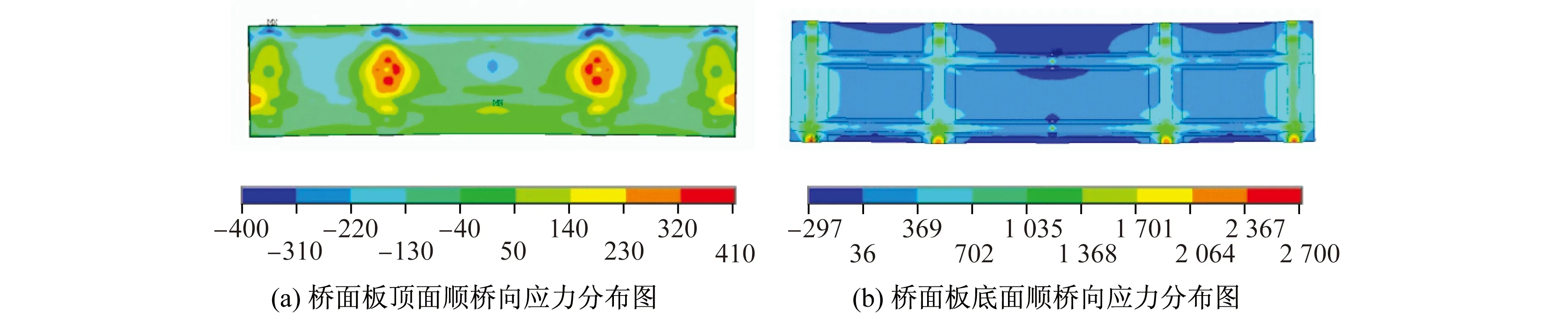
图4 混凝土桥面板顺桥向应力分布图(单位：kPa)

图5为混凝土桥面板横桥向应力分布图。可以看出，在收缩作用180天后，混凝土桥面板上表面横桥向应力在-0.6～1.2 MPa，混凝土桥面板下表面横桥向应力在-0.3～1.4 MPa。由于混凝土横桥向宽度较长，远大于顺桥向长度，因此混凝土横桥向收缩自应力水平大于顺桥向收缩自应力。由于横隔板翼缘是约束混凝土板横向收缩的主要因素，因此在横隔板翼缘附近混凝土板下缘横桥向拉应力较大，在0.3～1.4 MPa。在混凝土加腋端部，由于截面突变出现了拉应力集中。

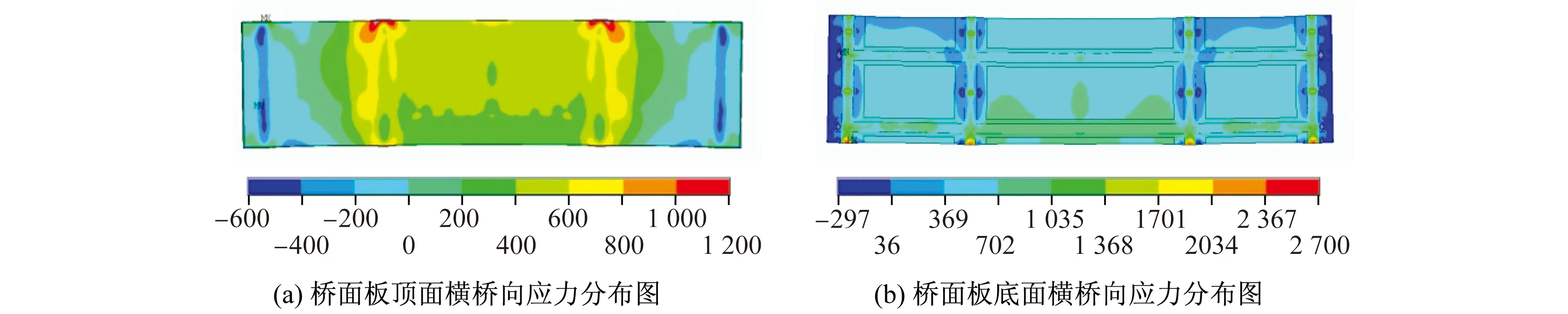
图5 混凝土桥面板横桥向应力分布图(单位：kPa)

图6为钢梁顺桥向应力分布图。可以看到，在收缩作用半年后，钢梁顺桥向总体应力在-14～2 MPa。在边腹板和中腹板的上翼缘，钢梁顺桥向压应力达到了较大水平，在-14～-10 MPa，而横隔板上翼缘的应力水平很小，为-3～0.2 MPa，与上文混凝土的顺桥向应力分布结果相对应，说明腹板及其上翼缘对混凝土顺桥向的收缩约束作用较大。由于混凝土对钢梁的反作用，所以钢梁应力随高度减小逐渐由压应力变为拉应力，约2 MPa。在斜底板上U肋和横隔板的交界处，有一定程度的应力集中。

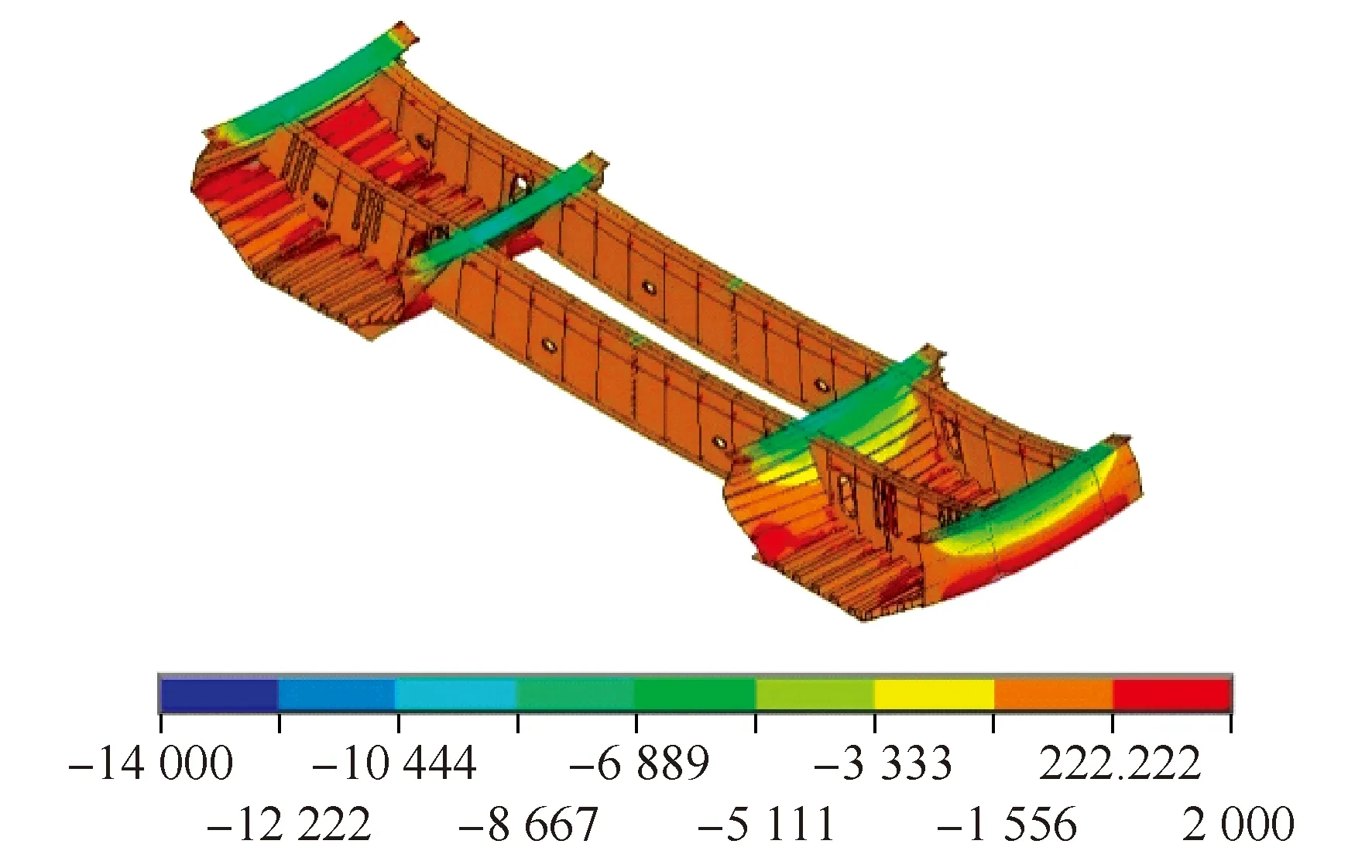
图6 钢梁顺桥向应力分布图(单位：kPa)

图7为钢梁横桥向应力分布图。可以看出，在收缩作用半年后，钢梁横桥向总体应力-14～2 MPa，基本和钢梁顺桥向应力水平持平。在两道横隔板上缘，钢梁横桥向压应力达到了较高水平，在-14～-8 MPa，与上文混凝土的横桥向应力分布结果相对应，说明横隔板及其上翼缘对混凝土横桥向的收缩约束作用比较大；在边腹板和中腹板上缘，钢梁应力水平在-5～0.2 MPa，其约束作用没有横隔板作用明显；钢梁中横向拉应力大部分发生在斜底板，主要是由于混凝土对钢梁的反作用，但拉应力不大，约2 MPa。在斜底板上U肋和横隔板的交界处，有一定程度的应力集中。

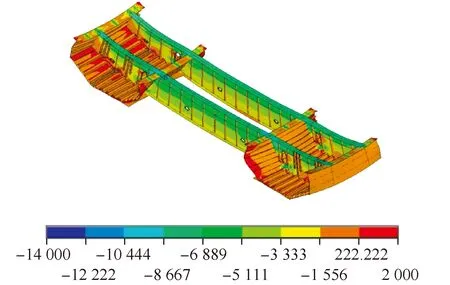
图7 钢梁横桥向应力分布图(单位：kPa)

综合上文的应力分析结果还可以得出，混凝土横桥向收缩拉应力水平要大于顺桥向收缩拉应力，这是由于组合箱梁预制节段横桥向宽度远大于顺桥向长度，可见预制节段长度对混凝土顺桥向应力影响显著。因此，可以预见，通过采用节段预制的方法，相比斜拉桥全跨整体浇筑混凝土桥面板的方法，能够减小混凝土收缩引起的顺桥向拉应力。

4.2 预制组合梁节段桥面板收缩自应力的影响因素

从上文可知，钢梁上的收缩自应力与钢梁强度相比，处于较低水平，因此应以控制混凝土桥面板的收缩自应力为主。

为考察混凝土桥面板收缩自应力的影响因素，分别以桥面板厚度、钢梁底板厚度、预制混凝土桥面板宽度、预制节段长度为单独控制变量，计算桥面板完成收缩量90%时的受力情况，并与标准节段进行对比。各分析工况参数如表1所示，其中，类型A—E分别对应标准截面、变混凝土板厚、变钢底板厚、变混凝土板宽、变混凝土板长的分析工况。

表1 预制节段截面特性表

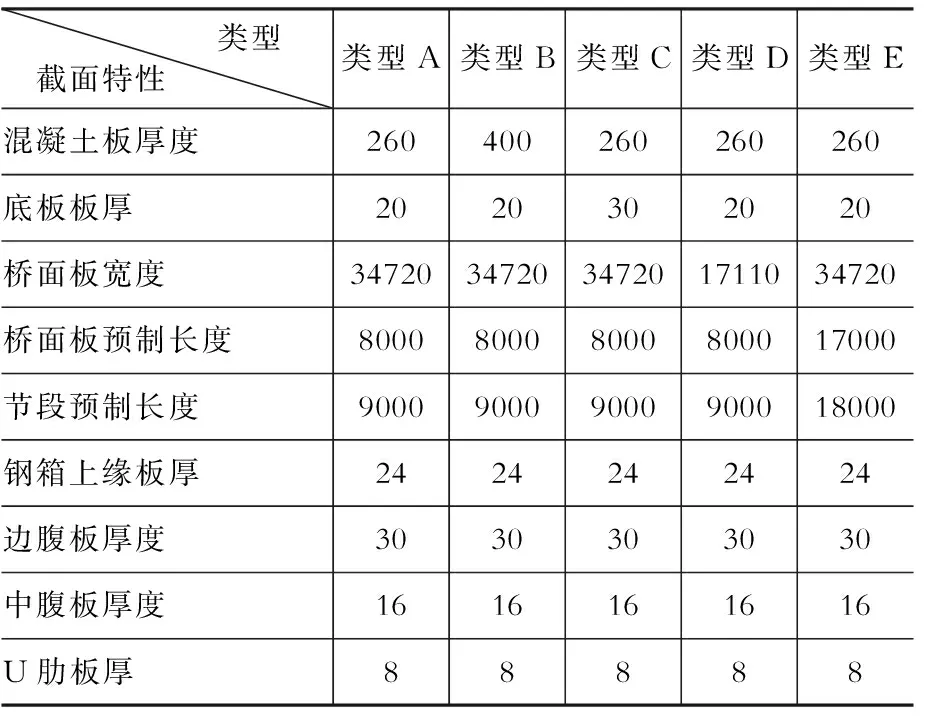
Table 1 Cross section properties of precast segments mm

为对混凝土桥面板的应力分布情况进行描述，采用图8中所示的三条线位置上的桥面板的顶面和底面应力、钢梁应力进行分析。3个截面如下：截面1是节段边缘与横隔板1间的中心线位置；截面2是横隔板1与横隔板2间的中心线位置；截面3是节段边缘与横隔板2间的中心线位置。

由于结构对称，这里只给出半幅桥面板计算结果，坐标系中x轴表示横桥向，原点位于桥面板横桥向跨中位置。

图9、图10为在各参数变化下，混凝土桥面板内的应力分布情况(以拉应力为正，压应力为负，应力变化以正值为增大)。

图8 预制节段选取截面示意图(单位：mm)

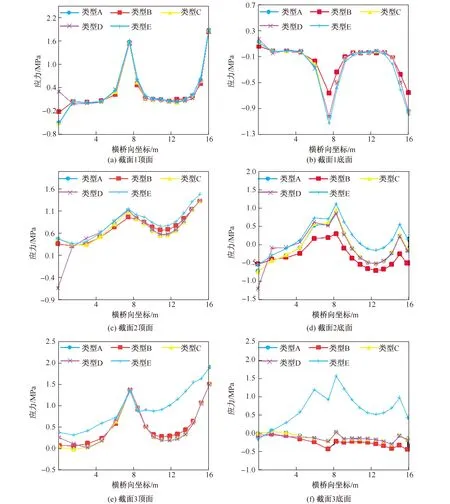
图9 桥面板顺桥向收缩自应力

从图9可知，各截面顺桥向应力在边腹板(x=16 m)和中腹板位置处(x=7.5 m)达到峰值，说明边腹板和中腹板是约束顺桥向收缩的主要因素。

混凝土板厚由260 mm变到400 mm时，板厚变化对混凝土桥面板的影响程度不同，从图9(a)，(c)，(e)可知，对混凝土板底面顺桥向应力影响较小，而对混凝土板顶面顺桥向应力影响大一些(图9(b)，(d)，(f))。当混凝土板厚变化时，混凝土板顶面顺桥向应力减小，幅值可达0.6 MPa(图9(d))。当板厚变厚时，钢梁和混凝土板间的约束内力变化不大，但由于混凝土的截面增大，因此，相应应力水平降低。

钢梁底板厚度由20 mm变到30 mm，由于钢梁底板变厚，钢梁的刚度变大，钢梁对混凝土的约束内力变大，约束自应力变大，所以混凝土桥面板的应力变化趋势是拉应力增大，压应力减小，这和图中曲线规律一致。但由于钢梁刚度增大有限，桥面板应力变化不明显，最大变化幅值也只有0.05 MPa，这表明改变钢梁截面刚度对混凝土板的收缩应力分布影响很小。

混凝土桥面板预制宽度由34.72 m变为17.11 m时，顺桥向应力除了在桥面板跨中附近小范围内(x=0～2 m)应力有一定变化，其余各位置几乎没有变化。混凝土桥面板预制宽度的变化，并不引起顺桥向刚度的显著变化，因此，顺桥向收缩自应力总体变化不大。

预制节段长度由8 m变为17 m时，桥面板各截面顺桥向应力变化不一。截面1位置应力几乎没有变化(图9(a)，(b))，这是因为截面1相对于组合梁节段自由端部的位置基本没有变化。截面2和3位置顺桥向应力发生明显变化(图9(c)，(d)，(e)，(f))，混凝土板顶面和底面应力均增大，增大幅值甚至达1.5 MPa(图9(f))。计算结果表明，随着预制节段长度的增大，混凝土板的顺桥向拉应力增大较为明显。

因此，当斜拉桥采用全跨整体浇筑混凝土桥面板的方法时，桥面板纵向长度将远远大于横向宽度，由此引起的混凝土收缩拉应力也将大大增加。至此，也论证了上文提到的，通过采用节段预制的方法，控制预制节段的长度，相比斜拉桥全跨整体浇筑混凝土桥面板的方法，能够减小混凝土收缩引起的顺桥向拉应力。

对比顺桥向应力曲线和横桥向应力曲线可知，顺桥向应力水平在-1.5～2.0 MPa，而横桥向应力水平达到-1.2～4 MPa。横桥向整体应力水平高于顺桥向应力，这是因为预制节段横桥向宽度远大于顺桥向长度的缘故。

从图10(b)可知，混凝土板厚由260 mm变到400 mm时，桥面板横向应力发生明显变化，各截面横向应力总体均减小，幅值达0.7 MPa。当板厚变化时，钢梁和混凝土板间的约束内力变化不大，但由于混凝土的截面增大，因此，相应应力水平降低。

钢梁底板厚度由20 mm变到30 mm，由于钢梁刚度增大有限，桥面板横桥向应力变化不明显，最大变化幅值也只有0.05 MPa，这表明改变钢梁截面刚度对减小混凝土桥面板的横桥向应力效果不显著。

从图10(c)可知，混凝土桥面板预制宽度由34.72 m变为17.11 m时，横桥向应力在桥面板跨中(x=0处)到中腹板(x=7处)范围内，变化显著，横桥向拉应力大幅减小，最大可达2 MPa；在中腹板至边腹板范围内，横桥向应力减少不明显。混凝土板宽的变化是通过在横桥向跨中设置了湿接缝实现的。由于在跨中设置了湿接缝，原来混凝土板横向跨中位置的约束被释放，因此，横桥向应力在桥面板跨中到中腹板范围内有效减小。计算结果表明，控制混凝土板宽能够有效减小混凝土板内横桥向收缩应力。

混凝土板长由8 m变为17 m时，各截面横桥向应力变化不一。在中腹板和边腹板处，横向应力变化不大；腹板间的混凝土板横桥向应力变化显著。图10(b)表明，截面1跨中位置和截面2跨中位置横桥向应力均明显减小，幅值可达1 MPa；图10(e)表明，截面3处的横桥向应力增大，幅值达0.6 MPa。截面3处的变化趋势与截面1和2处相反的原因是，原来截面3位于节段的纵向边缘，在预制节段长度变化后，截面3位置变成位于节段纵向跨中，周围混凝土对其收缩有约束作用。计算结果表明，随着预制节段长度的增大，混凝土板的顺桥向应力增大明显，而横桥向应力却有一定程度的减小。

5 结 论

本文采用有限元方法，对椒江二桥预制组合梁节段混凝土桥面板收缩自应力进行计算分析，可以得到以下结论：

(1) 钢梁腹板上翼缘是阻碍混凝土纵向收缩的主要约束，因此，钢梁腹板上翼缘承受较大顺桥向压应力，混凝土桥面板加腋处承受较大顺桥向拉应力；横隔板翼缘是约束混凝土板横向收缩的主要因素，因此，在横隔板处的混凝土桥面板下缘横桥向拉应力水平较高，钢横隔板上翼缘横桥向压应力较大。

(2) 由于预制节段横桥向宽度远大于顺桥向长度，因此混凝土桥面板横桥向收缩应力水平要高于顺桥向收缩应力。

(3) 增大混凝土桥面板板厚能一定程度降低混凝土板收缩自应力；改变钢梁截面板厚对减小混凝土板的应力水平影响很小；控制混凝土桥面板板宽能够有效减小混凝土板内横桥向收缩应力；控制混凝土桥面板长度能够有效减小混凝土板内顺桥向收缩应力。

图10 桥面板横桥向收缩自应力

(4) 预制组合箱梁节段长度对混凝土顺桥向应力影响显著，在斜拉桥中通过减少组合梁纵桥节段长度能够有效减少混凝土的顺桥向拉应力。

(5) 其他断面型式组合梁混凝土收缩影响规律有待研究。

[ 1 ] 严国敏.现代斜拉桥[M].成都：西南交通出版社，1996.

Yan Guomin. Modern cable stayed bridge[M]. Chengdu: South West Communications Press, 1996. (in Chinese)

[ 2 ] 刘玉擎.组合结构桥梁[M]. 北京：人民交通出版社，2005.

Liu Yuqin. Steel-concrete hybrid bridge[M]. Beijing: China Communications Press, 2005. (in Chinese)

[ 3 ] 邵长宇.钢-混凝土箱形结合梁斜拉桥在东海大桥的应用与展望[J].桥梁建设,2003,(3):5-8.

Shao Changyu. Application and prospective of cable-stayed of steel-concrete composite box girder for east China Sea bridge[J]. Bridge Construction, 2003,(3): 5-8. (in Chinese)

[ 4 ] 吴冲,曾明根,邵长宇,等. 大跨度组合箱梁斜拉桥混凝土收缩与徐变应力分析[J]. 世界桥梁,2004,S1:37-41.

Wu Chong, Zeng Minggen, Shao Changyu, et al. Analysis of concrete shrinkage and creep stresses of long-span composite box girder cable-stayed bridges[J]. World Bridges, 2004, S1:37-41. (in Chinese)

[ 5 ] 周履,陈永春.收缩徐变[M]. 北京：中国铁道出版社，1994.

Zhou Lu, Chen Yongchun. Shrinkage and creep[M]. Beijing: China Railway Press, 1994. (in Chinese)

[ 6 ] 温庆杰,叶见曙. 钢-混凝土组合梁的收缩徐变效应分析[J].工业建筑,2006,S1:492-495.

Wen Qingjie, Ye Jianshu. Shrinkage and creep effects of steel concrete composite beams[J]. Industrial Construction, 2006,S1:492-495. (in Chinese)

[ 7 ] 林辉旭,蔡忠明.杨浦大桥主桥上部结构施工工艺[J].桥梁建设,1993,4:10-14.

Lin Huixu, Cai Zhongming. Construction of the superstructure of the Shanghai Yangpu Bridge[J]. Bridge Construction, 1993, 4: 10-14. (in Chinese)

[ 8 ] 张金斗.上海南浦大桥主桥上部结构施工工艺[J].土木工程学报,1992,25(6):17-24.

Zhang Jindou. Construction of the superstructure of the Shanghai Nanpu Bridge[J]. China Civil Engineering Journal, 1992,25(6): 17-24. (in Chinese)

[ 9 ] 上海徐浦大桥[J]. 城市道桥与防洪,1998,1:38.

Shanghai Xupu Bridge [J]. Urban road bridges and flood contol, 1998,1: 38. (in Chinese)

[10] 高宗余.青洲闽江大桥结合梁斜拉桥设计[J].桥梁建设,2001,4:13-17.

Gao Zongyu. Design of composite girder cable stayed bridge over Minjiang River at Qingzhou[J]. Bridge Construction, 2001, 4: 13-17. (in Chinese)

[11] 中华人民共和国交通部.JTG D62—2004 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. 北京：人民交通出版社，2004.

Ministry of Transport of the People’s Republic of China. JTG D62—2004 Code for design of highway reinforced concrete and prestressed concrete bridges and culverts[S]. Beijing: China Communications Press, 2004. (in Chinese)

Concrete Shrinkage Stresses Analysis of Precast Composite Girder Segments

ZENG Minggen1CHEN Wenchao2,*SU Qingtian2

(1. The Architectural Design and Research Institute of Tongji University, Shanghai 200092, China;2. Department of Bridge Engineering, Tongji University, Shanghai 200092)

Mechanical behaviors of the precast composite girder segments due to concrete shrinkage were analyzed by using the shell solid elements during finite element modeling. It is found that the stress distribution of tensile stress on the bridge deck and compressive stress in the steel beam is complex. Through further comparative analyses of mechanical behaviors of the precast composite girder by considering parameters such as deck thickness, steel beam slab thickness, deck width, and precast segmental length, it is concluded that concrete longitudinal stress was significantly affected by the precast segmental length. The decrease of the longitudinal segment length can effectively reduce the longitudinal concrete tensile stress induced by shrinkage in composite beam for a cable-stayed bridge.

precast composite girder, concrete shrinkage, finite element model

2013-10-10

*联系作者，Email: 1031083821@qq.com