斜拉桥索塔锚固区塔壁简化计算的等效受力高度取值研究

贺国栋 石雪飞 阮 欣

(同济大学桥梁工程系，上海 200092)

斜拉桥索塔锚固区塔壁简化计算的等效受力高度取值研究

贺国栋*石雪飞 阮 欣

(同济大学桥梁工程系，上海 200092)

提出斜拉桥索塔锚固区混凝土塔壁的等效受力高度概念，以确保其平面框架简化模型能够合理反映结构的实际受力状态。在考虑桥塔整体变形和塔壁相互嵌固作用的基础上，通过空间有限元计算和回归分析，采用参数拟合给出了塔壁等效受力高度的简化计算公式。经过有限元计算值和公式值的误差对比分析，表明计算公式在常用参数范围内具有较高的精度。

斜拉桥, 索塔锚固区, 混凝土塔壁, 简化计算, 等效受力高度

1 索塔锚固区概述

斜拉桥锚固区混凝土塔壁的水平受力性能直接影响其配筋计算和结构尺寸的确定。塔壁的横向受力复杂，空间效应明显，一般采用三维实体有限元分析，然而平面杆系结构作为土木工程中最简单也最实用的简化结构，便于工程师掌握，因此，提出塔壁的杆系简化计算方法也尤为必要。索塔锚固区斜拉索一般沿塔高方向等间距离散分布，若取其中某一高度的桥塔标准节段进行简化框架分析，用于混凝土塔壁水平配筋的预估和检验，既能反映锚固区的实际受力情况，又简化了计算分析对象[1-2](图1)。

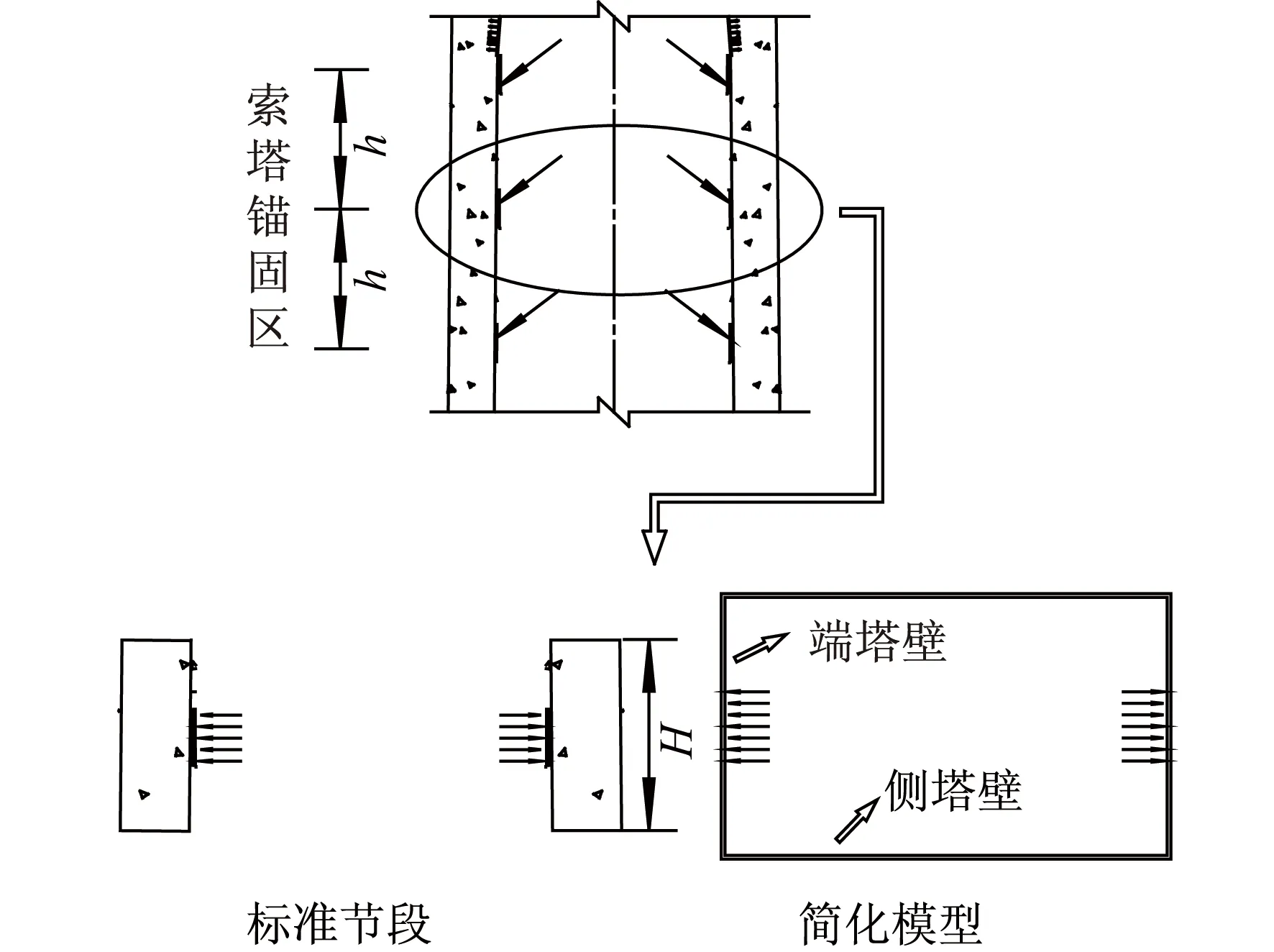
图1 索塔锚固区及标准节段

关于索塔锚固区混凝土塔壁的简化计算方法，国内外已有一些研究，其简化模型一般取高度等于塔上索距h的桥塔节段进行计算分析[3-4]，这种简化方法实际上是认为端塔壁的横向弯矩沿塔高方向均匀分布。然而，取高度为索距h的桥塔节段进行简化是否合理，国内外文献还尚未有相关研究。理论上塔壁的力学响应是所有斜拉索作用叠加之后的效应，但实际上相邻第二对拉索之外的影响已经很小，为此，本文在考虑相邻索相互作用的前提下，基于理论分析研究，提出索塔锚固区混凝土塔壁框架简化的桥塔节段高度选取方法，供同类结构设计计算提供参考和借鉴。

2 塔壁等效受力高度概念

2.1 等效受力高度的提出

由索塔锚固区的构造特点可知，斜拉索的水平分力通过混凝土齿块或钢板等传递至塔壁[5-6]，最终作用于混凝土塔壁的荷载分布面积较小，塔壁更加接近于多点集中受荷状态，荷载作用下塔壁横向弯矩沿塔高方向将出现较大的不均匀性。

图2显示了利用ANSYS建立的桥塔空间梁格模型在三对索力作用下，端塔壁中点的横向弯矩沿塔高方向的分布情况，足见弯矩分布的不均匀性。如果对塔壁进行简化框架分析时，直接选取高度等于斜拉索塔上索距h的节段进行简化计算，将过大考虑了荷载的扩散效应，对于弯矩极值点而言，其计算结果是偏危险的。

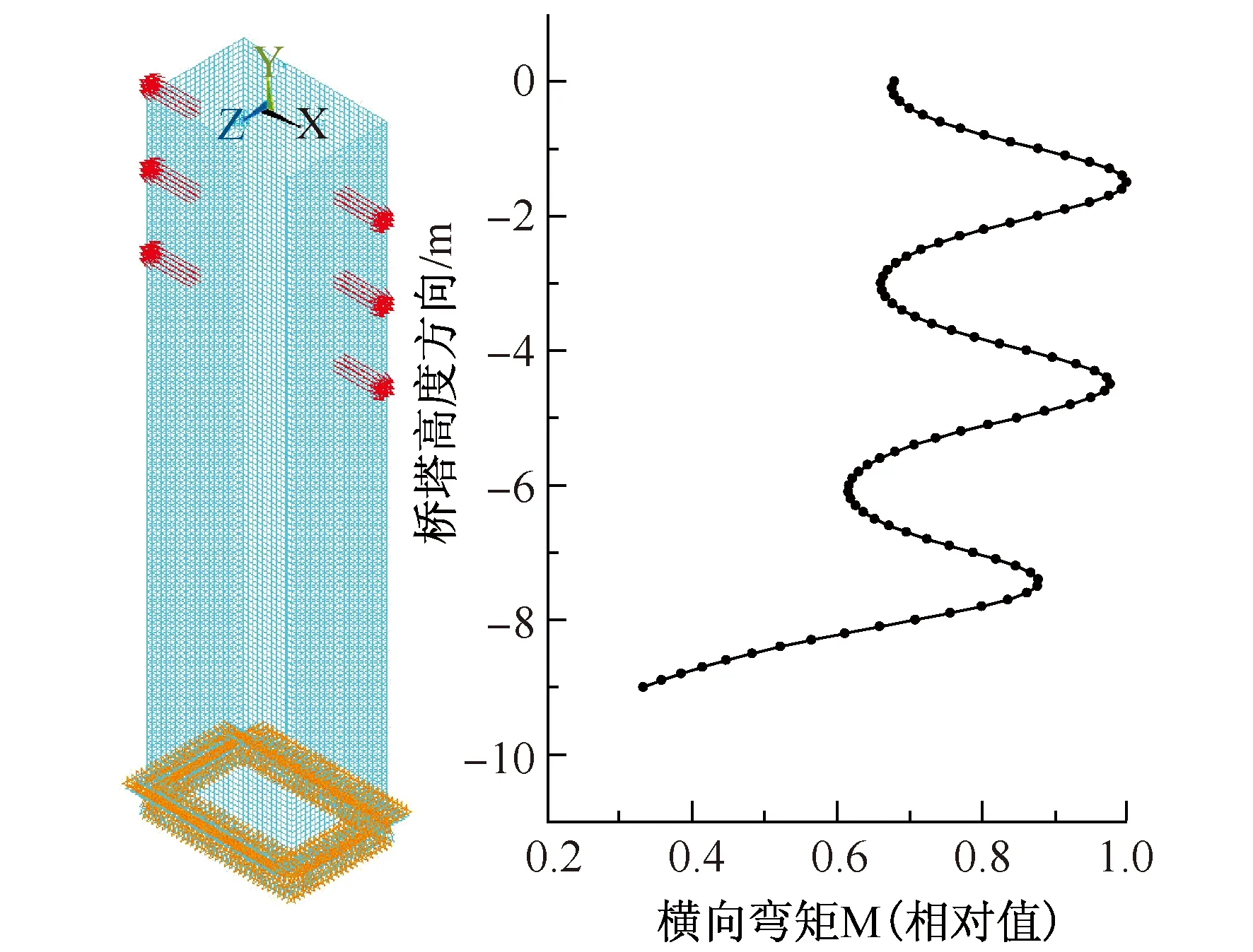
图2 索力作用下塔壁弯矩沿高度分布图

为了确保简化框架模型能够较为真实反映结构的实际受力状态，不能直接选取高度等于斜拉索索距的节段进行简化计算。为此，本文提出混凝土塔壁的等效受力高度概念，用于确定简化框架的桥塔节段选取高度。

端塔壁受力示意如图3所示。当荷载以a×b的面积作用在桥塔端塔壁上时，塔壁除了沿横桥向x产生挠曲变形，沿高度方向y也必然发生挠曲变形。即在荷载作用下，不仅直接受荷的高度为a的塔壁受力，相邻部分也参与工作，共同承受水平荷载产生的弯矩[7]。

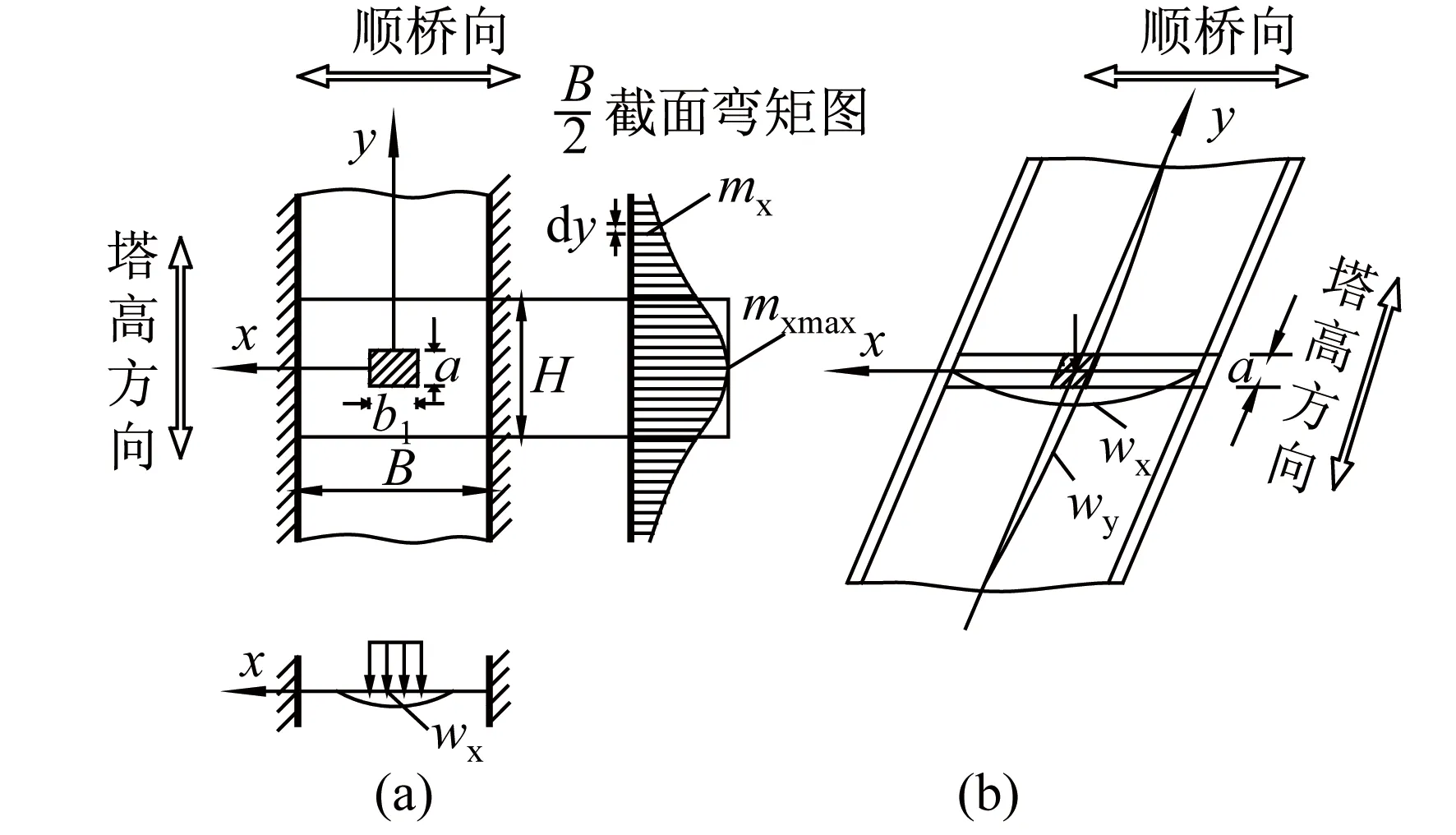
图3 端塔壁受力示意图

设想以高度为H的塔壁均匀承受水平荷载产生的总弯矩，即：

(1)

式中M——荷载产生的总弯矩；

mxmax——荷载中心处的最大分布弯矩。

则定义等效受力高度为

(2)

式(2)实际上确定了塔壁等效受力高度的计算原理。

2.2 塔壁等效受力高度与桥面板有效分布宽度的区别

混凝土塔壁的等效受力高度与桥面板的有效分布宽度在原理上类似，《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)[8](以下简称《规范》)基于理论研究，提出了桥面板在车轮荷载作用下的有效分布宽度计算公式。《规范》给出的有效分布宽度公式由于对边界条件的理想假定，忽略了顶板、翼缘板和腹板的相互嵌固作用及扭曲变形对彼此的影响，也忽略了结构整体挠曲和扭转等变形对应力分布的影响，与实际情况存在一定的差异[9]，适应于柔性板。

对于桥塔而言，其刚度较大，与柔性板的受力特点有所区别。并且侧塔壁刚度与端塔壁刚度接近，不能忽略侧塔壁的弯曲变形和嵌固作用对端塔壁受力的影响。因而，有必要结合桥塔的结构特点，进行定量的参数分析，提出适应于桥塔简化的等效受力高度计算公式。

3 等效受力高度的影响参数分析

3.1 影响参数

根据等效受力高度的定义分析可知，影响混凝土塔壁的等效受力高度的因素主要是桥塔截面尺寸及荷载作用形式[10]，具体包括如下参数：端塔壁宽度B、端塔壁厚度d、侧塔壁长度L、侧塔壁厚度t、荷载作用高度a、塔上索距h(图4)。本文基于计算分析，采用控制变量法研究各个参数对H的影响方式和影响因子，试图拟合等效受力高度H的计算公式。

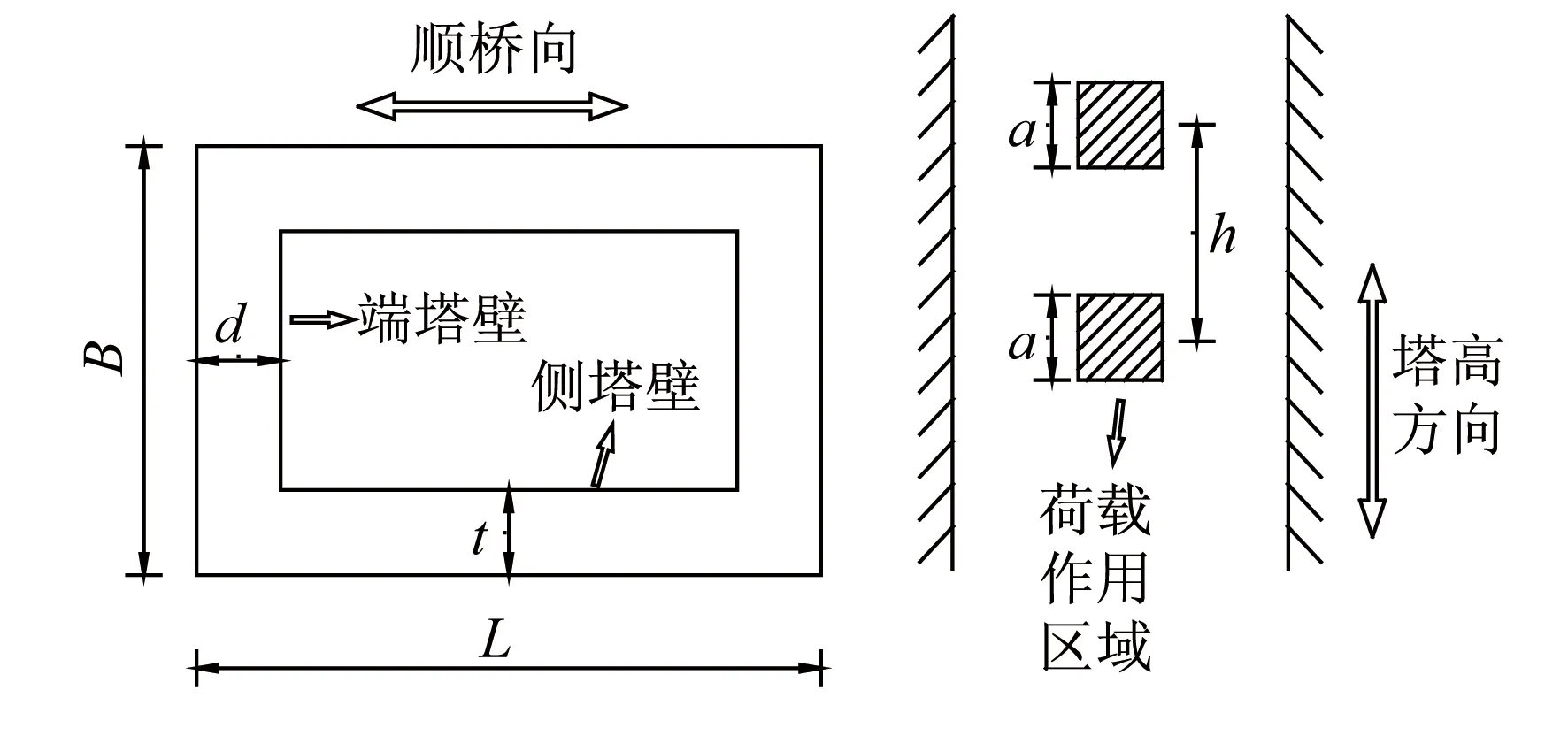
图4 塔壁参数示意图

根据表1中斜拉桥塔柱截面尺寸统计情况以及现有斜拉桥索塔锚固区的构造特点，端塔壁宽度B一般为4～8 m，端塔壁厚度d一般为0.6～1.2 m，侧塔壁长度L一般为6～9 m，侧塔壁厚度t一般为0.6～1.2 m，荷载作用高度a一般为0.2～1.0 m，塔上索距h一般为2～4 m。本文关于等效受力高度的参数分析，也是在这6个参数的常用取值范围内进行。

表1 桥塔截面尺寸统计[11]

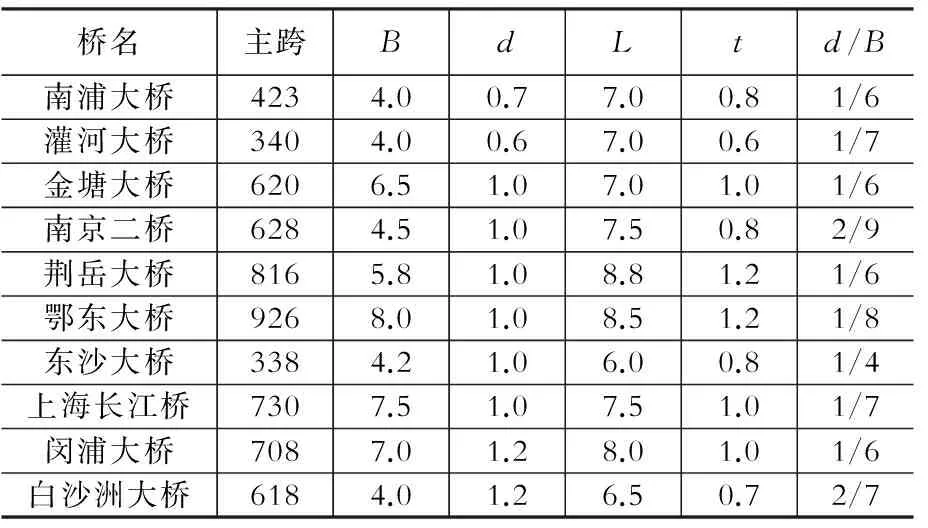
Table 1 Statistics of pylon section dimension m

为了寻找H与各个参量的关系，本文在考虑桥塔整体变形和侧壁嵌固作用的基础上，采用ANSYS程序建立桥塔的空间实体模型，对桥塔模型的5个参数取多种数值进行分析。在实体模型中，考虑了三对索力的影响，并在计算关心的3个桥塔节段下方构造了20 m高度的桥塔单元，将桥塔底部固结，以减小边界条件对计算结果的影响。

根据横向应力与横向弯矩等效的原则，采用积分法求解总弯矩，再按式(2)求解等效受力高度。采用控制变量法研究各个参数对H的影响，最终通过回归分析，提出了塔壁等效受力高度的计算公式。

3.2 参数敏感性分析

在有限元模型中，以B=5 m,d=1 m,L=7 m,t=1 m,a=0.4 m,h=3 m为基准参数，采用控制变量法逐一研究单个变量对等效受力高度的影响，利用最小二乘法线性拟合和二次曲线拟合H与各参数之间的联系方程。例如，研究端塔壁宽度B对等效受力高度的影响时，控制d=1 m,L=7 m,t=1 m,a=0.4 m,h=3 m五个参数不变，分别取B=3 m, 4 m,5 m,6 m,7 m，得到与B值一一对应的等效受力高度H，通过回归分析，拟合H与B之间的联系方程。图5—图10显示了H与各参数之间的关系和联系方程。

(1) 端塔壁宽度B变化的敏感性分析

在索力作用下，端塔壁以受弯为主，其受力模式接近于两端弹性嵌固板，端塔壁宽度B越大，则板的跨度越大，板的柔性也越大，因而索力的扩散效应也更加明显。

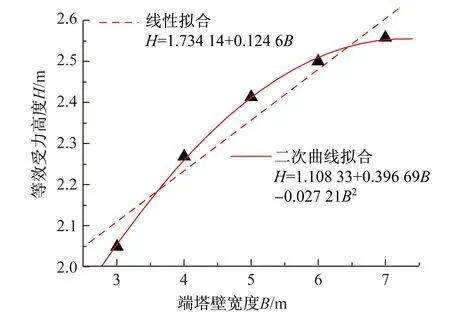
图5 H与B的关系曲线和方程

表2H-B公式误差分析

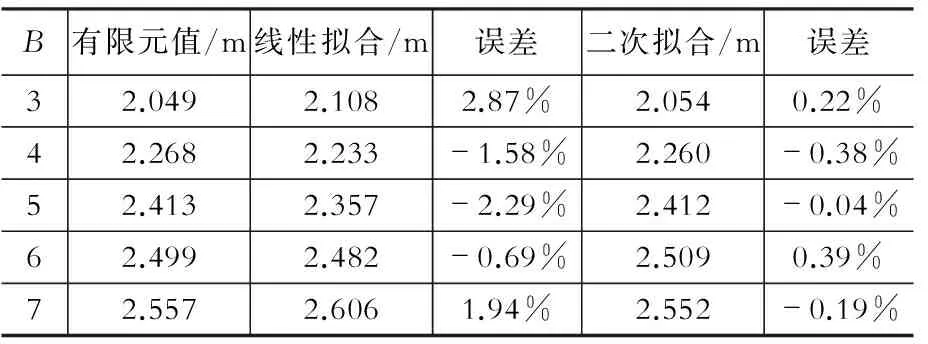
Table 2 Error analysis of H-B formula

(2) 端塔壁厚度d变化的敏感性分析

端塔壁厚度大小直接影响到索力从塔壁内侧到外侧的局部扩散，d越大，扩散效应越明显。

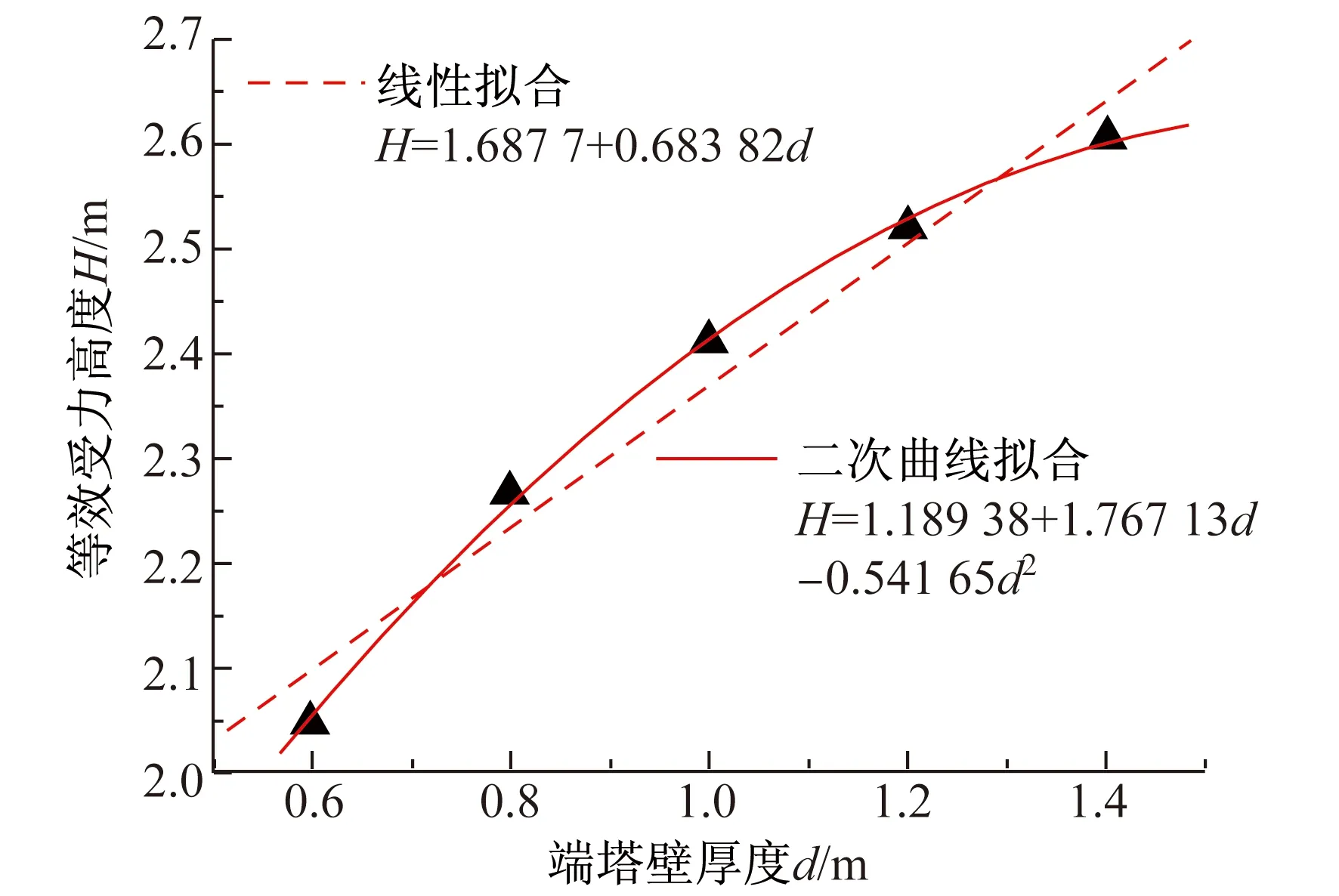
图6 H与d的关系曲线和方程

表3H-d公式误差分析

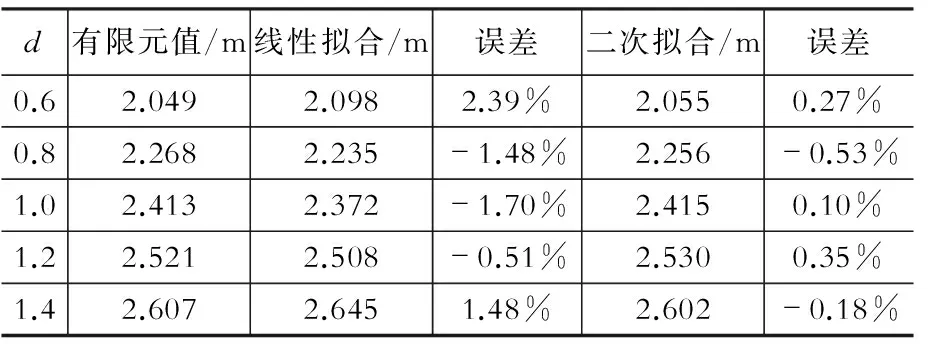
Table 3 Error analysis of H-d formula

(3) 有侧塔壁长度L变化的敏感性分析

在锚固区，侧塔壁对端塔壁起到弹性嵌固的

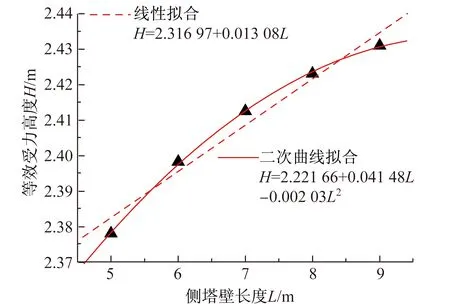
图7 H与L的关系曲线和方程

作用，侧塔壁长度L越大，则侧塔壁越柔，其嵌固作用越弱，从而使得端塔壁的柔性也越大，索力的扩散效应更加明显。

表4H-L公式误差分析

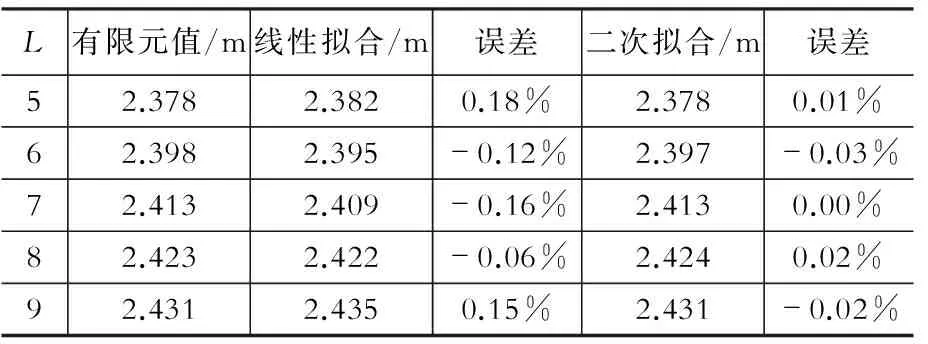
Table 4 Error analysis of H-L formula

(4) 侧塔壁厚度t变化的敏感性分析

由于侧塔壁对端塔壁起到弹性嵌固的作用，侧塔壁厚度t越大，则侧塔壁刚度越大，其嵌固作用越强，从而使得端塔壁的刚性也越大，索力的扩散效应更小。

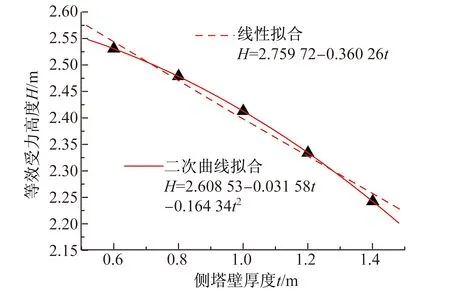
图8 H与t的关系曲线和方程

表5H-t公式误差分析

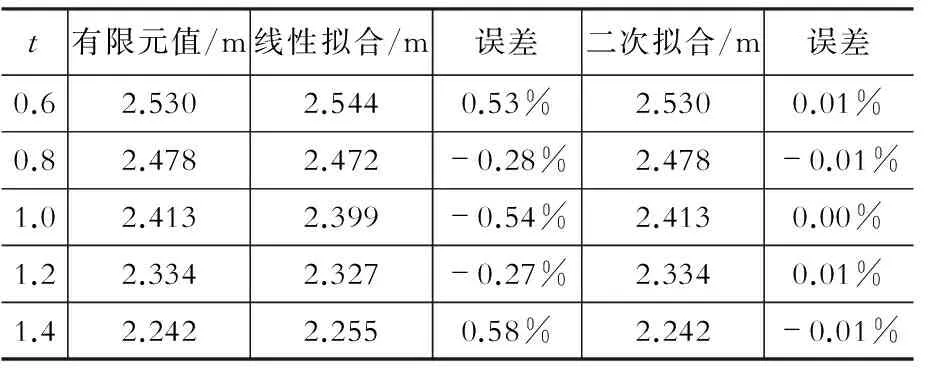
Table 5 Error analysis of H-t formula

(5) 荷载作用高度a变化的敏感性分析

在锚固区，荷载作用高度(即锚板或锚固齿块与塔壁沿高度方向的接触范围)越大，则共同承担索力的塔壁节段高度越大，具体的影响关系如图9所示。

(6) 塔上索距h变化的敏感性分析

由H与各参数之间的关系图及其误差分析表格可知：H-B的线性拟合的最大误差为2.87%，

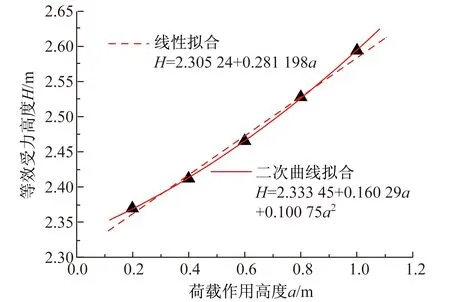
图9 H与a的关系曲线和方程

表6H-a公式误差分析

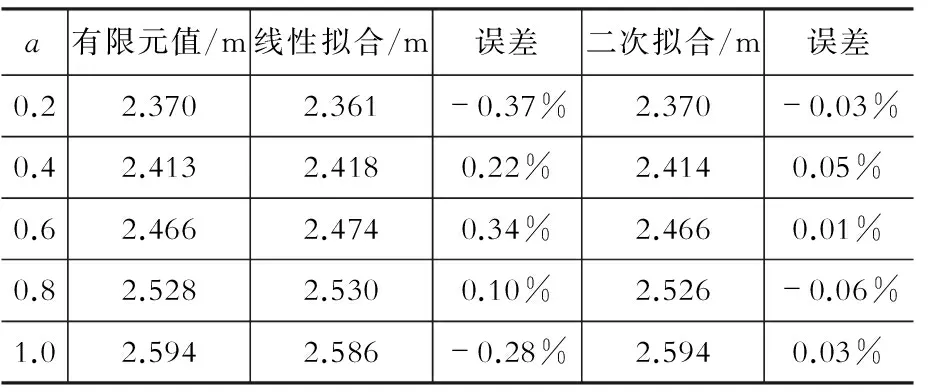
Table 6 Error analysis of H-a formula

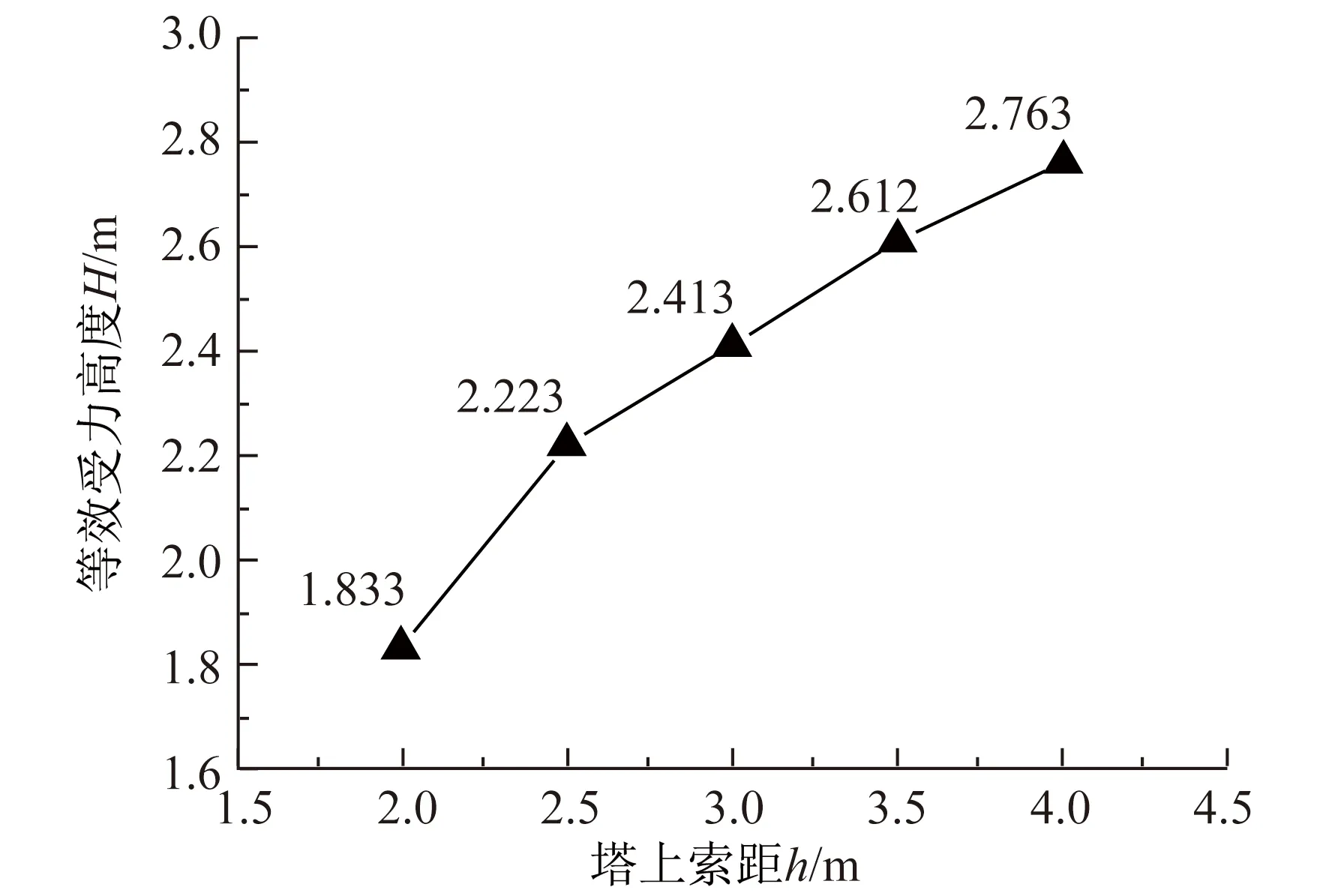
图10 H与h的关系曲线

二次曲线拟合的最大误差仅为0.38%，采用二次曲线具有更高的精度；H-d的线性拟合的最大误差为2.39%，二次曲线拟合的最大误差仅为0.53%，采用二次曲线具有更高的精度；H-L的线性拟合的最大误差为0.18%，二次曲线拟合的最大误差仅为0.03%，采用线性拟合已经具有足够的精度；H-t的线性拟合的最大误差为0.58%，二次曲线拟合的最大误差仅为0.01%，采用线性拟合已经具有足够的精度；H-a的线性拟合的最大误差为0.37%，二次曲线拟合的最大误差仅为0.06%，采用线性拟合已经具有足够的精度。因此，从公式的精确性和简洁性考虑，建立H与B，d的关系时拟采用二次曲线，建立H与L，t，d的关系时拟采用直线。H与各参数的关系方程分别为

(3)

由于式(3)是建立于索距h=3 m的情形，考虑不同索距h的影响时，可采用适当的修正系数β。利用图10数据结果求得修正系数如表7所示，对于不在表格中列出的其他h值对应的β值，可采用线性内插求得。

表7 修正系数β表格

Table 7 Correction factor β

3.3 回归计算公式

上节绘制了等效受力高度H与各个参数B，d，L，t，a的相关曲线，并通过最小二乘拟合得到各自的影响方程。最终H的计算公式应是如下形式：

(4)

式中，C为待定常数表示除了B，d，L，t，a5个参数外的其他参数对塔壁等效受力高度H的影响。

利用式(4)以及式(3)建立的H与单个变量的5个方程，分别代入已确定的参数，可求得对应的常数C值：

C1—C5数值均较小，最大不超过0.0453 m即4.53 cm，可见除B，d，L，t，a5个参数外的其他参数对塔壁等效受力高度的影响较小。故取C1—C5的平均值作为最终的C值，求得C=0.0380，因此混凝土塔壁的等效受力高度计算公式为

H=β(0.038 0+0.396 69B-0.027 21B2

+1.767 13d-0.541 65d2+0.013 08L

(5)

-0.360 26t+0.281 198a)

式(5)各参数的单位均为m。修正系数β的取值见表7。

3.4 适应范围

为验证计算公式的精确性，表8列出了等效受力高度的公式计算值与有限元计算值的误差，最大误差不超过1.61%。可见在常用参数范围内，计算公式具有较高的精度。

表8 公式计算值及与有限元值的对比

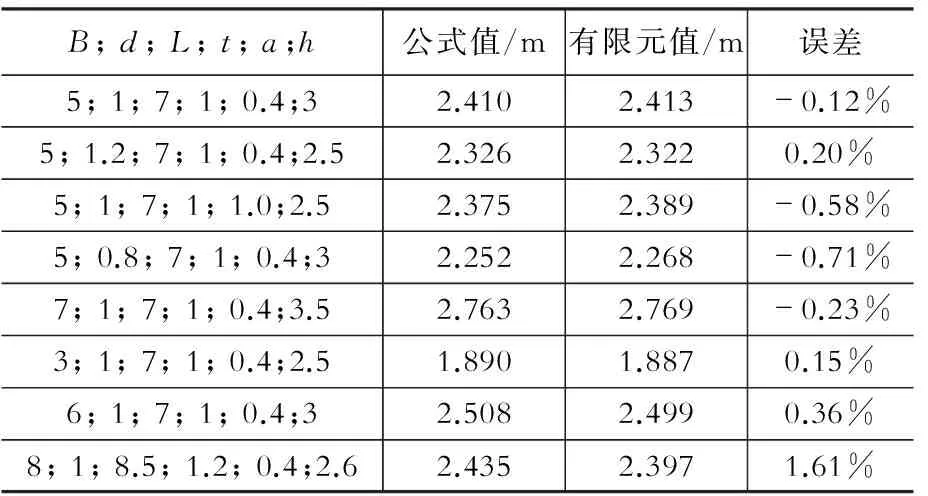
Table 8 Result comparison between the proposed method and the FEA

另一方面，为验证简化框架计算的可行性，将采用框架模型按本文公式算得的弯矩，与采用空间实体模型积分得到的弯矩进行对比，两者误差约为6.5%，表明本文提出的简化方法具有一定的工程意义。

4 结 论

本文通过对斜拉桥索塔锚固区的构造特性分析和混凝土塔壁的有限元计算，以及计算结果的回归分析，主要得出以下结论：

(1) 有限元计算结果表明，索塔锚固区由于作用于塔壁的荷载分布面积较小，塔壁更加接近于多点集中受力状态，荷载沿塔高方向的扩散高度较小，索力作用下端塔壁横向弯矩沿高度方向分布出现较大的不均匀。如果直接选取高度等于斜拉索索距的节段进行简化计算，将过大估计了荷载的扩散能力，其简化计算结果是偏危险的。

(2) 本文提出混凝土塔壁的等效受力高度概念，在考虑桥塔整体变形和侧壁嵌固作用的基础上，通过空间有限元计算和回归分析，建立了塔壁等效受力高度H关于端塔壁宽度B、端塔壁壁厚d、侧塔壁长度L、侧塔壁壁厚t、荷载作用高度a5个参量的关系。

(3) 提出等效受力高度H的计算公式，常用参数范围内(端塔壁宽度B为3～8 m，端塔壁厚度d为0.6～1.4 m，侧塔壁长度L为5～9 m，侧塔壁厚度t为0.6～1.4 m，荷载作用高度a为0.2～1.0 m，塔上索距h为2～4 m)，计算公式具有较高的精度。

(4) 本文提出的等效受力高度的计算公式，并取该高度的桥塔节段进行梁单元简化分析，用于混凝土塔壁水平配筋的预估和检验，既能反映锚固区的实际受力情况，又简化了计算分析对象。

[ 1 ] 汪昕,吕志涛.斜向索力下钢-混凝土组合索塔锚固区荷载传递与分配关系分析[J].东南大学学报(自然科学版),2006,36(4):585-589.

Wang Xin, Lu Zhitao. Load transferring and distribution in anchorage zone of stell-concrete composite pylon under cable forces[J]. Journal of Southeast University (Natural Science Edition), 2006, 36(4): 585-589. (in Chinese)

[ 2 ] 张奇志,尹夏明,郑舟军.钢锚梁索塔锚固区受力机理分析与约束方式比选[J].桥梁建设,2012,42(6):50-56.

Zhang Qizhi,Yin Xiaming, Zheng Zhoujun. Analysis of force mechanism and comparison of restraint ways for steel anchor beam anchorage zone in pylon[J]. Bridge Construction, 2012, 42(6): 50-56. (in Chinese)

[ 3 ] 陈向阳,王昌将,史方华.大跨径斜拉桥钢锚梁的创新设计[J].公路,2009,(1):130-132.

Chen Xiangyang, Wang Changjiang, Shi Fanghua. The innovative design of long span cable-stayed bridge with steel anchor beam[J]. High Way, 2009,(1): 130-132. (in Chinese)

[ 4 ] 华新.斜拉桥索塔钢锚箱与塔壁混凝土拉力分配简化分析[J].现代交通技术,2006,3(1):26-29.

Hua Xin. Simplified method about tension distributing between steel anchorage box and concrete pylon wall on the anchorage section of pylon of cable-stayed bridge[J]. Modern Transportation Technology, 2006, 3(1): 26-29. (in Chinese)

[ 5 ] 苏庆田,秦飞.组合索塔锚固区水平受力机理的理论与试验[J].同济大学学报(自然科学版),2011,39(8):1120-1125.

Su Qingtian, Qin Fei. Theory and experiment on horizontal mechanical behavior in anchorage zone of composite cable-pylon[J]. Journal of Tongji University (Natural Science), 2011, 39(8):1120-1125. (in Chinese)

[ 6 ] 胡贵琼,郑舟军.荆岳长江公路大桥钢锚梁索塔锚固区单节段模型有限元分析[J].世界桥梁,2010,(3):40-44

Hu Guiqiong, Zheng Zhoujun. Finite element analysis of single sectional model of cable to pylon steel anchor beam anchor zone of Jingyue Changjiang river highway bridge[J]. The World Bridge, 2010, (3):40-44. (in Chinese)

[ 7 ] 邵旭东.桥梁工程[M]. 北京:人民交通出版社,2007.

Shao Xudong. Bridge engineer[M]. Beijing: China Communications Press, 2007. (in Chinese)

[ 8 ] 中华人民共和国交通部. JTG D62—2004公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:人民交通出版社, 2004.

Ministry of Transport of the Reople’s Republic of China. JTG D62—2004 Code for design of highway reinforced concrete and prestressed concrete bridges and culverts [S]. Beijing: China Communications Press, 2004. (in Chinese)

[ 9 ] 方志,张志田.钢筋混凝土变截面箱梁横向受力有效分布宽度分析[J].湖南大学学报(自然科学版),2003, 30(6):82-85.

Fang Zhi, Zhang Zhitian. The effective distribution width of the transverse internal force in RC box girders with varied section[J]. Journal of Hunan University (Natural Science Edition), 2003, 30(6): 82-85. (in Chinese)

[10] 许崇法.桥面板有效工作宽度的几何参数敏感性分析[J].山东交通科技,2007,(3):37-41.

Xu Chongfa. The analysis of influencing geometry parameter for the effective distribution width of bridge deck[J]. Shandong Jiaotong Keji, 2007,(3): 37-41. (in Chinese)

[11] 中国公路学会桥梁与结构工程分会.面向创新的中国现代桥梁[M]. 北京:人民交通出版社, 2009.

Bridge and Structural Engineering Branch of China Highway Society. Innovation-oriented contemporary Chinese bridges[M]. Beijing: China Communications Press, 2009. (in Chinese)

Equivalent Height Value of Anchorage Zone Wall Cable-stayed Bridges

HE Guodong*SHI Xuefei RUAN Xin

(Department of Bridge Engineering, Tongji University, Shanghai 200092, China)

To ensure the validity of a simplified framework model, this paper proposed the concept of equivalent distribution height in the concrete tower anchorage zone for a bridge pylon. By considering the overall deformation of the pylon and wall anchorage mechanism, the formula for the equivalent distribution height calculation were derived through finite element and regression analyses. The proposed formula was proved to provide satisfactory results within the parameter range.

cable-stayed bridge, anchorage zone, concrete tower, simplified calculation, equivalent height

2014-01-15

*联系作者，Email: heguodong_mail@126.com