一种计算复杂天线散射截面的新型快速方法
2015-02-17张忠祥孔勐陈明生张量吴先良
张忠祥 孔勐,2 陈明生 张量 吴先良,2
(1.合肥师范学院电子信息工程学院,合肥 230601;
2.安徽大学电子信息工程学院,合肥 230601)
一种计算复杂天线散射截面的新型快速方法
张忠祥1孔勐1,2陈明生1张量1吴先良1,2
(1.合肥师范学院电子信息工程学院,合肥 230601;
2.安徽大学电子信息工程学院,合肥 230601)
摘要针对传统数值算法分析天线结构项单站雷达散射截面(Radar Cross Section, RCS)问题运算量大的缺点,基于压缩感知理论引入一种包含各个离散入射角度信息的新型激励源,借助有限元软件的建模分析功能,形成一种适用于处理复杂天线结构项单站RCS的快速算法.通过对单极子天线、角锥喇叭天线和抛物面反射天线等算例的仿真,验证了新算法处理复杂目标能力强、计算效率高的优势.
关键词压缩感知;天线;电磁散射;快速计算
A novel method of RCS fast calculation with complex
资助项目: 国家自然科学基金(51477039,51207041); 安徽省高校重点项目(KJ2014A199,KJ2014A206); 安徽省科技计划项目(1501021041); 合肥师范学院"电磁场与微波技术"科研团队项目(kytd2015006)
联系人: 陈明生 E-mail: mschen@hftc.edu.cn
引言
随着现代战争中隐身技术的快速发展,天线的电磁散射问题越来越引起国内外学者的关注.然而,传统的数值方法在处理天线电磁散射问题时,存在着一些不足.一方面在分析天线单站雷达散射截面(Radar Cross Section, RCS)时,传统数值算法必须重复计算各个离散入射角度激励下的矩阵方程,耗费大量计算资源.另一方面,由于天线的结构项散射场[1-2]主要由天线外形结构决定,加之天线结构各异,传统算法的数值建模过程较为复杂.因此,传统数值算法在天线电磁散射特性分析中的发展受到了大大的限制.
压缩感知(Compressed Sensing, CS)[3-9]作为近年来发展迅速的高效信号处理方法,已被广泛应用到天线设计分析、微波成像等领域中.例如Hawes M B, Wei Liu等人利用CS对稀疏阵列天线的阵元位置进行分析,显著提高了该问题的优化效率[10-11];文献[12]将CS应用到多输入多输出(Multiple-Input/Multiple-Output, MIMO)阵列天线优化设计算法中,形成了一种有效的系统解决方案;文献[13]根据线性阵列天线的特性,引入CS理论构建了一种高分辨率逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISRA)成像框架.虽然诸多文献说明CS理论与天线技术的结合已显示出了极大的优越性,但是少有学者利用CS理论对天线的电磁散射问题进行分析.
基于CS理论,引入一种包含各个离散入射角度的新型激励源,利用有限元软件的建模分析功能构建各种天线的数值模型,并计算出新入射源激励下的天线回波结构项散射场的测度,反复计算数次,获得新激励源多次照射下的观测值,然后采用正交匹配追踪 (Orthogonal Matching Pursuit,OMP)[14-16]算法恢复出各实际入射角照射下天线的原始回波散射场,进而计算出天线结构项单站RCS.由于该方法中测度的次数要少于传统算法中入射角的逐点计算次数,故该算法能够减少运算量,提升计算效率.
1压缩感知理论框架
2006年,Candès等人首先提出CS理论[17],该理论在信号获取的同时,即对数据进行压缩,而无须像传统信号处理方法那样进行采样、压缩、传输和解压,其能将数据采集和压缩合二为一[18],被美国科技评论评为2007年度十大科技进展.压缩感知的执行过程由观测矩阵的设计、信号的稀疏化和信号的重构三个部分构成[19],其原理如下.
设计一个平稳的、与观测对象不相关的观测矩阵ΦM×N,对原始信号XN×1进行观测,有
YM×1=ΦM×NXN×1.
(1)
寻找关于原始信号X的合适的稀疏表示为
α=ψX.
(2)
式中: ψ为正交变换矩阵; α为稀疏向量.
应用正交匹配追踪算法,借助稀疏表示,通过较少的观测值YM×1恢复出原始信号.该过程等价于求解如下规划问题:
(3)
为计算方便,其可近似修正为
(4)
根据文献[20],若满足
(5)
则精确重构概率将大于1-4e-C2M,其中K由K-稀疏性(K-Sparse)决定,可理解为原始信号通过稀疏变换后对精确重构至关重要的K个关键信息,C1、C2为常数项系数.
在给定M的情况下,在恢复过程引入的稀疏变换越合适,K值会越小,式(5)越容易满足,恢复概率就越高,从而稀疏变换就显得十分关键.
2新型快速计算方法
有限元方法的基本原理是通过对目标的离散、函数插值,结合相应边界条件构建方程组
Dx=d,
(6)
然后进行求解.式中: D为系数矩阵; x为响应矩阵; d为激励向量.
在处理天线单站RCS问题时,为了减少传统数值方法的运算量,以CS理论为基本框架,构建一种包含各个实际入射角度的新型激励源,即将所有的离散入射角度重复进行M次随机叠加,构成以下新型入射激励矩阵元素为
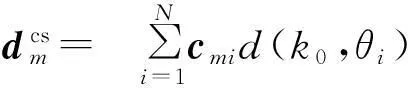
m=1,2,3,…,M,i=1,2,3,…,N.
(7)
式中:N为入射角度的离散数;k0为相应波数;θi为入射角;cmi为随机矩阵元素.
将式(7)代入式(6)可得
(8)
式中由矩阵元素cmi所构成的随机矩阵即为压缩感知理论中的观测矩阵ΦM×N.
一般可选择高斯、贝努利随机矩阵及随机部分傅里叶矩阵、稀疏带状随机、托普利兹或循环以及稀疏列随机、循环矩阵等作为观测矩阵以高概率满足精确重构条件,本文选择高斯随机矩阵进行实验.

(9)
简而言之,原始信号的观测值可以通过式(8)中的线性激励求解,而非计算出式(9)中的真实x(k0,θi)再观测.
针对一般的非稀疏响应矩阵,须构建一个正交变换矩阵ΨN×N进行稀疏化处理,从而获取原始响应矩阵在正交变换矩阵下的稀疏表示.
为了提高计算效率,选择第二类切比雪夫多项式构造稀疏变换[21],其递推关系可描述为
(10)
式中Ui(x)的定义区间为[-1,1],作如下变换
t=cosx
(11)
则-1≤t≤1,因此取
ti=cosxi,i=1,2,…,n
(12)
可得到U0(t),U1(t),U2(t),…,Un-1(t),根据ti的取值不同,可得到所需要的稀疏变换矩阵,其矩阵表达式为
(13)
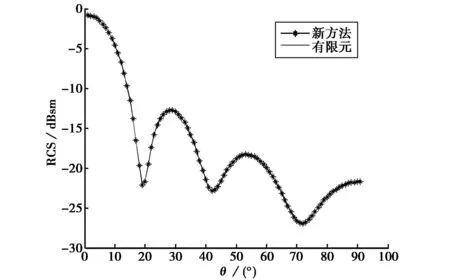
在分析新型激励入射天线的单站RCS问题时,根据CS理论,构造新型激励,结合有限元软件的建模和分析功能,获得N个实际入射角度响应的M个测量值(M 3计算实例与分析 为了验证新型快速计算方法的有效性,对单极子天线、角锥喇叭天线、抛物面反射天线的结构项单站RCS进行仿真,其中观测矩阵和稀疏变换矩阵分别采用高斯随机矩阵和第二类切比雪夫稀疏变换基,恢复算法采用OMP算法,定义相对均方根误差如下: (14) 设频率为3.0 GHz的水平方向极化平面波入射一连接金属板的单极子天线,该天线极子长度为7.5 cm,极子半径为0.25 cm,金属板与极子的馈电间距为0.25 cm,金属板尺寸为15 cm×15 cm.分别采用借助有限元仿真软件与CS理论相结合的新型快速计算方法和传统有限元算法对单极子天线的结构项单站RCS进行分析,计算范围为φ=0°,θ=0°~90°,其中有限元法以离散入射角1°为步长逐点计算,结果如图1所示. 图1 单极子天线的结构项单站RCS(φ=0°,θ=0°~90°) 表1所示新型快速计算方法较传统有限元算法在计算次数和计算时间上明显减少,且恢复误差为0.58%. 表1 两种方法计算单极子天线的数据比较 针对一角锥喇叭天线,其波导段尺寸为0.9cm×0.4cm,波导段长度为1.0cm;喇叭口径为1.8cm×1.4cm,喇叭段长度为3.0cm.采用频率为10GHz,水平极化的平面波入射该喇叭天线,分别计算φ=0°,θ=0°~180°和φ=0°~180°,θ=90°范围内目标的单站RCS,将计算结果与有限元软件仿真结果进行比较,如图2、图3所示.其中有限元软件按照1°为角度步长旋转181次,逐点完成目标单站RCS的数据采集.表2展示了两种方法分别对角锥喇叭天线的两个主平面计算的相关数据. 图2 角锥喇叭天线的结构项单站RCS(φ=0°,θ=0°~180°) 图3 角锥喇叭天线的结构项单站RCS(φ=0°~180°,θ=90°) 表2 角锥喇叭天线的计算数据比较 采用新方法对结构如图4所示的抛物面反射天线进行分析,入射波为10GHz水平极化的平面波.该天线反射面由抛物线方程y2=800mm×x构造,其反射面口径为460mm×300mm,馈源采用15dB标准增益矩形喇叭天线.图5显示了新方法计算φ=90°,θ=-180°~180°范围内的目标单站RCS与有限元软件逐点仿真相比较的结果. 图4 抛物面反射天线结构图 图5 抛物面反射天线的结构项单站RCS(φ=90°,θ=-180°~180°) 表3给出了抛物面反射天线的计算分析与比较,通过表3中的数据可见,新方法的处理次数约为软件仿真处理次数的1/3,而误差为2.46%. 表3 抛物面反射天线的计算数据比较 为了描述新方法中原始信号恢复误差与计算次数M之间的关系,统一针对以上例子进行分析,其中稀疏变换矩阵均采用第二类切比雪夫稀疏变换基,结果如图6所示.由图可见,针对以上算例,当新方法的压缩比(M/N)在25%~35%之间时,其恢复精度均可达到工程需求,从而说明该方法具备一定的通用性和有效性. 根据CS原理,为了保证信号的恢复精度,M的取值与原始信号的实际个数N及其在稀疏域中的稀疏系数K之间应满足M≈Klg(N/K)≪N的关系.由此可见,若以减小M次数来提高计算效率作为新方法的优化方向,其关键应在于提升原始信号的稀疏化程度,而针对不同目标,依靠先验知识获取合适的稀疏矩阵将成为解决该问题的切入点.新方法先验知识的获取,可通过以下步骤得以实现.首先对已构建的新型激励源进行展开,其次提取相关信息,由于响应信号与激励源具有相同的稀疏特性,因此可针对激励源的组成特点,最终构造出适合响应信号的稀疏变换矩阵. 图6 计算的响应信号恢复误差与压缩比之间的关系 4结论 文章在压缩感知的理论框架下,构建了一种适用于目标宽角度计算的新型激励源,并利用仿真软件对天线目标进行建模分析,结合恢复算法,形成一种计算复杂天线结构项RCS的新型快速方法.实验结果表明,新方法在处理天线的结构项单站RCS问题方面,计算效率大大提高,通过与复杂结构天线逐点计算值的比较,说明了该方法具备一定的工程实用性.最后,针对新方法的计算次数与重构误差之间的关系进行了分析,并指出了新方法的后续优化方向. 参考文献 [1]万国宾, 张红霞, 万伟, 等.带罩天线散射计算的子平面波技术[J]. 电波科学学报,2008,23(3):417-421. WANGuobin,ZHANGHongxia,WANWei,etal.EquivalentplanewavetechniqueforRCScomputationofradomeenclosedantennas[J].ChineseJournalofradioScience, 2008, 23(3): 417-421.(inChinese) [2]姜文. 天线散射机理分析与RCS控制技术研究[D].西安:西安电子科技大学,2012. JIANGWen.AnalysisofAntennaScatteringMechanismandtheResearchonRCSControlTechnology[D].Xi’an:XidianUniversity,2012. (inChinese) [3]PEYREG.Bestbasiscompressedsensing[J].IEEETransactionsonSignalProcessing, 2010,58(5): 2613-2622. [4]DUARTEMF,ELDARYC.Structuredcompressedsensing:fromtheorytoapplications[J].IEEETransactionsonSignalProcessing, 2011, 59(9): 4053-4085. [5]WEISJ,ZHANGXL,SHIJ.LineararraySARimagingviacompressedsensing[J].ProgressinElectromagneticsResearch, 2011,117:299-319. [6]CHOSH,LEESH,CHANNG,etal.Fastterahertzreflectiontomographyusingblock-basedcompressedsensing[J].OpticsExpress, 2011, 19(17):16401-16409. [7]NIZW,ZHANGMX,LIJ,etal.Imagecompressedsensingbasedondatadrivenadaptiveredundantdictionaries[J].ProgressinElectromagneticsResearchM, 2011, 22: 73-89. [8]YUS,KHWAJAAS,MAJ.Compressedsensingofcomplex-valueddata[J].SignalProcessing, 2012, 92(2): 357-362. [9]石光明, 刘丹华, 高大化, 等. 压缩感知理论及其研究进展[J].电子学报, 2009, 37(5):1070-1081. SHIGuangming,LIUDanhua,GAODahua,etal.Advancesintheoryandapplicationofcompressedsensing[J].ActaElectronicaSinica, 2009, 37(5):1070-1081.(inChinese) [10]HAWESMB,LIUW.Robustsparseantennaarraydesignviacompressivesensing[C]//18thInternationalConferenceonDigitalSignalProcessing.Fira:IEEE, 2013:1-5. [11]HAWESMB,LIUW.Compressivesensing-basedapproachtothedesignoflinearrobustsparseantennaarrayswithphysicalsizeconstraint[J].IETMicrowaves,Antennas&Propagation, 2014, 8(10):736-746. [12]ZHONGLihua,HUDonghui,DINGChibiao.ISARimagingbasedonantennaarrayandcompressedsensing[C]//IEEECIEInternationalConferenceonRadar.Chengdu:IEEE,2011:1547-1550. [13]DAIC,ZHOUL,WUXLY.OptimalMIMOarrayforcompressivesensingimageformation[J].JournalofElectromagneticWavesandApplications, 2014, 28(16): 2049-2058. [14]DAIW,MILENKOVICO.Subspacepursuitforcompressivesensingsignalreconstruction[J].IEEETransactionsonInformationTheory, 2009, 55(5): 2230-2249. [15]黄传禄, 晁坤, 毛云志. 基于压缩感知的空间谱估计[J].电波科学学报, 2014, 29(1):150-157. HUANGChuanlu,CHAOKun,MAOYunzhi.Thespatialspectrumestimationbasedoncompressivesensing[J].ChineseJournalofRadioScience,2014,29(1):150-157.(inChinese) [16]王建, 盛卫星, 韩玉兵, 等.基于压缩感知的圆阵自适应数字波束形成算法[J]. 电波科学学报, 2014, 29(3): 455-461. WANGJian,SHENGWeixing,HANYubing,etal.Compressedsensingbasedadaptivedigitalbeamformingalgorithmincirclearrays[J].ChineseJournalofRadioScience, 2014, 29(3): 455-461.(inchinese) [17]CANDESEJ,TAOT.Nearoptimalsignalrecoveryfromrandomprojections:universalencodingstrategies[J].IEEETransactionsonInformationTheory, 2006, 52(12): 5406-5425. [18]BARANIUKRG.Compressivesensing[J].IEEESignalProcessingMagazine, 2007, 24(4): 118-120. [19]RAUHUTH,SCHASSK,VANDERGHEYNSTP.Compressedsensingandredundantdictionaries[J].IEEETransactionsonInformationTheory, 2008, 54(5): 2210-2219. [20]BARANIUKRG,DAVENPORTMA,DEVORER,etal.Asimpleproofoftherestrictedisometrypropertyforrandommatrices[J].ConstructiveApproximation,2008, 28(3): 253-263. [21]CAOXY,CHENMS,WUXL.Sparsetransformmatricesandtheirapplicationinthecalculationofelectromagneticscatteringproblems[J].ChinesePhysLett, 2013, 30(2): 028401. 张忠祥 (1976-),男,安徽人,合肥师范学院电子信息工程学院副教授,博士,研究方向为电磁场数值计算、天馈系统设计分析. 孔勐(1983-),男,安徽人,合肥师范学院电子信息工程学院讲师,安徽大学博士研究生,研究方向为计算电磁学混合算法. 陈明生(1981-),男,安徽人,合肥师范学院电子信息工程学院教授,博士,博士生导师,研究方向为计算电磁学快速算法、压缩感知理论的应用. 刘晓娣, 周新力, 肖金光, 等. 一种地形条件下电波传播入射余角估计算法[J]. 电波科学学报,2015,30(6):1211-1217. doi: 10.13443/j.cjors. 2015010601 LIU Xiaodi, ZHOU Xinli, XIAO Jinguang, et al. A grazing angle estimation algorithm of wave propagation over terrain[J]. Chinese Journal of Radio Science,2015,30(6):1211-1217. (in Chinese). doi: 10.13443/j.cjors. 2015010601 antenna structure ZHANG Zhongxiang1KONG Meng1,2CHEN Mingsheng1 ZHANG Liang1WU Xianliang1,2 (1.SchoolofElectronicandInformationEngineering,HefeiNormalUniversity, Hefei230601,China;2.SchoolofElectronicandInformationEngineering, AnhuiUniversity,Hefei230601,China) AbstractA novel excitation source with more incident angle information is proposed based on compressive sensing (CS) theory, to overcome the traditional calculation difficulties. With the help of the Finite Element Software, a fast computational method of calculation mono-static radar cross section (RCS) is presented. The calculation results of monopole antenna,pyramidal horn antenna and parabolic antenna have verified the accuracy and computational efficiency of the new method. Key wordscompressive sensing; antenna; electromagnetic scattering; fast computational method 作者简介 收稿日期:2014-10-30 中图分类号TN011 文献标志码A 文章编号1005-0388(2015)06-1205-06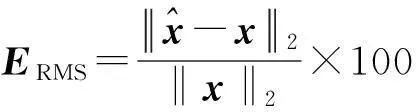
3.1 单极子天线

3.2 角锥喇叭天线



3.3 抛物面反射天线



3.4 误差分析

