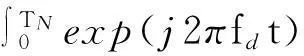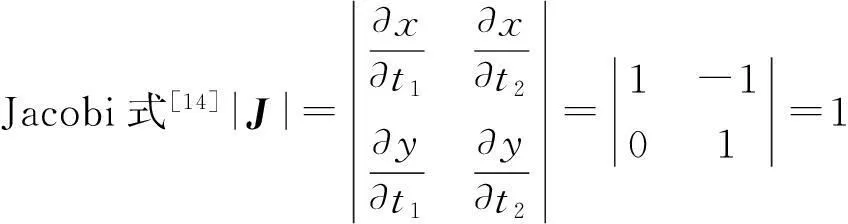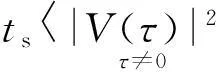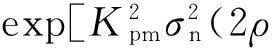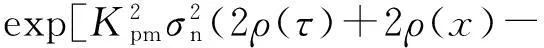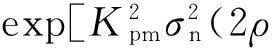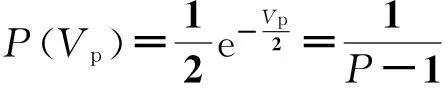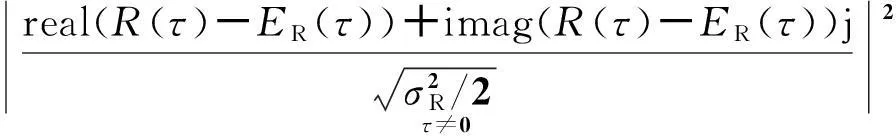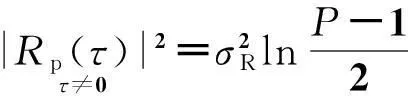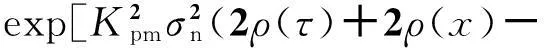噪声调相连续波雷达统计主旁瓣比推导和分析

吕婧　顾红　苏卫民　薄超

(南京理工大学电子工程技术研究中心,南京 210094)



噪声调相连续波雷达统计主旁瓣比推导和分析

吕婧顾红苏卫民薄超

(南京理工大学电子工程技术研究中心,南京 210094)

摘要噪声调相连续波雷达(Noise Phase Modulated Continuous Wave Radar, NPM-

CWR)脉压输出旁瓣表现为具有随机特性的噪声基底,通过对其统计规律的研究,推导了NPMCWR的统计主瓣均方旁瓣比(Statistical Mainlobe to Mean Square Sidelobe Ratio,SMMSSR)和统计主瓣峰值旁瓣比(Statistical Mainlobe to Peak Sidelobe Ratio,SMPSR)的数学表达式.分析了NPMCWR的脉压输出统计主旁瓣比与脉压长度、目标多普勒、有效相移等参数之间的关系.数学表达式的计算结果与Monte-Carlo仿真结果很好地吻合,验证了推导结论的正确性.

关键词噪声调相连续波;脉压;主旁瓣比;噪声雷达;多普勒

资助项目: 教育部博士点基金(20113219110018); 国家自然科学基金(61471198); 中国航天科技集团公司航天科技创新基金(CASC04-02)

联系人： 顾红 E-mail：guhong666@126.com

引言

随机噪声连续波雷达是一种以微波噪声或噪声调制信号为发射信号的雷达.发射信号的随机性使得雷达具有“图钉”形模糊函数,具有无模糊测距、测速性能,实现良好的距离、速度分辨力[1].另外,由于其同时具有优良的低截获概率(Low Probability of Intercept, LPI)、电磁兼容能力(Electro Magnetic Compatibility, EMC)、电子反对抗(Electronic Counter-Countermeasures, ECCM)能力,在日益复杂的电磁环境下具有很好的应用价值,越来越受到人们的重视,被广泛研究应用于监视雷达、合成孔径雷达、防撞雷达、穿地探测雷达、穿墙雷达等领域[2-6].

常用的噪声调制方式有噪声调幅、噪声调相、噪声调频.不同的调制方式和参数的选取会影响发射信号功率谱形状、多普勒敏感性以及脉压输出主旁瓣比特性.工程实现时需根据目标特点结合发射信号特性,从雷达作用距离、调制带宽、旁瓣要求等角度综合考虑选择调制方式和波形参数.随机噪声连续波雷达脉压输出主旁瓣比与脉压长度、多普勒频率、调制指数等参数的关系,对于雷达检测的目标散射截面积(Radar Cross Section,RCS)和速度的动态范围设计具有重要意义.相关方面的研究目前已有一些成果,如文献[7]对噪声调幅连续波雷达的脉压主旁瓣比进行了推导分析.文献[8]给出了噪声调频连续波的统计主旁瓣比的数学表达式.文献[9-10]中给出了噪声调相雷达相关输出的表达式,并对相关输出的旁瓣做了讨论,但并未对主旁瓣比进行深入理论分析和仿真.文献[11]推导了伪码调相连续波雷达的主旁瓣数学表达式,但伪随机信号仍具有周期性,不属于随机噪声信号.上述文献均未对噪声调相连续波雷达的统计主旁瓣比进行深入讨论.文中从噪声调相连续波雷达(Noise Phase Modulated Continuous Wave Radar, NPMCWR)的相关输出表达式入手推导了NPMCWR的脉压输出主瓣均方旁瓣比和主瓣峰值旁瓣比的数学表达式,对影响主瓣均方旁瓣比和主瓣峰值旁瓣比的参数进行了分析.由于发射信号是随机信号,其旁瓣电平也是随机的,只有通过统计指标描述其性能,所以文中推导的脉压输出主瓣均方旁瓣比和主瓣峰值旁瓣比应为统计值,分别称之为统计主瓣均方旁瓣比(Statistical MainlobetoMeanSquareSidelobeRatio,SMMSSR)和统计主瓣峰值旁瓣比(Statistical Mainlobe to Peak Sidelobe Ratio,SMPSR).计算机Monte-Carlo仿真数据与理论推导结果能够很好地吻合,验证了文中结论的正确性.

1NPMCWR信号模型及脉压处理

NPMCWR发射信号复数表达式为[12]

St(t)=Aexp{j[2πf0t+Kpme(t)]}.

(1)

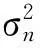
调制高斯白噪声e(t)的概率密度函数为

(2)

设调制噪声e(t)通过低通滤波器后的带宽为Be(t),噪声调相信号St(t)的带宽为B,则带宽B的表达式为[12]：

当Kpmσn≫1时,发射的NPMCW信号带宽为

B=1.36KpmσnBe(t)；

(3)

当Kpmσn≪1时,发射的NPMCW信号带宽为

B=2Be(t).

(4)

St(t)=Aexp{j[2πf0t+θ(t)]}.

(5)

假设存在单点目标,以速度vr沿雷达径向做匀速运动,初始时刻与噪声调相连续波雷达的距离为R0,回波信号幅度为Ar,回波信号相对发射信号的延迟时间为tr,则噪声调相连续波的回波信号复数表达式为

Sr(t)=Arexp{j[2πf0(t-tr)+θ(t-tr)]}.

(6)

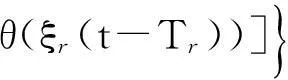
(7)

回波信号按帧进行划分,依次与各距离门延迟后的参考信号进行相关积累.每帧信号通常在时域划分为若干个等长无重叠分段,分别对各分段进行脉压,对同一个距离门的脉压输出沿段间慢时间进行傅里叶变换可得距离-多普勒二维信息.这里研究某分段脉压输出的统计特性,其脉压处理框图如图1所示.

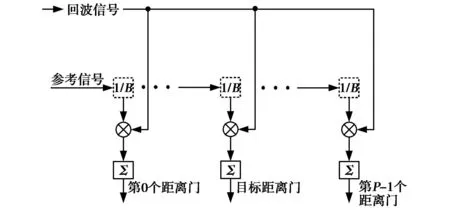
图1　NPMCWR回波分段脉压处理框图

将发射信号以1/B为延迟单位,进行多级延时后作为参考信号,可表示为

Sc(t)=Acexp{j[2πf0(t-Tc)+θ(t-Tc)]}.

(8)

式中: Ac为参考信号的幅度; Tc为参考信号相对于发射信号的时延,且是1/B的倍数.

回波信号与参考信号的互相关即为NPMCWR的脉压输出结果,可表达为

(t-Tc)]}×exp{j[θ(ξr(t-Tr))-

θ(t-Tc)]}dt

=ArAcexp[j2π(f0τ-fdTr)]×

Tr))-θ(t-Tc)]}dt.

(9)

式中: fd=f0ξd; τ=Tc-Tr; *表示复共轭; TN为噪声调相连续波雷达信号某段的相关积累时长.当Tc=Tr时,脉压输出为白噪声背景下的最佳线性滤波器输出,即脉压输出峰值.

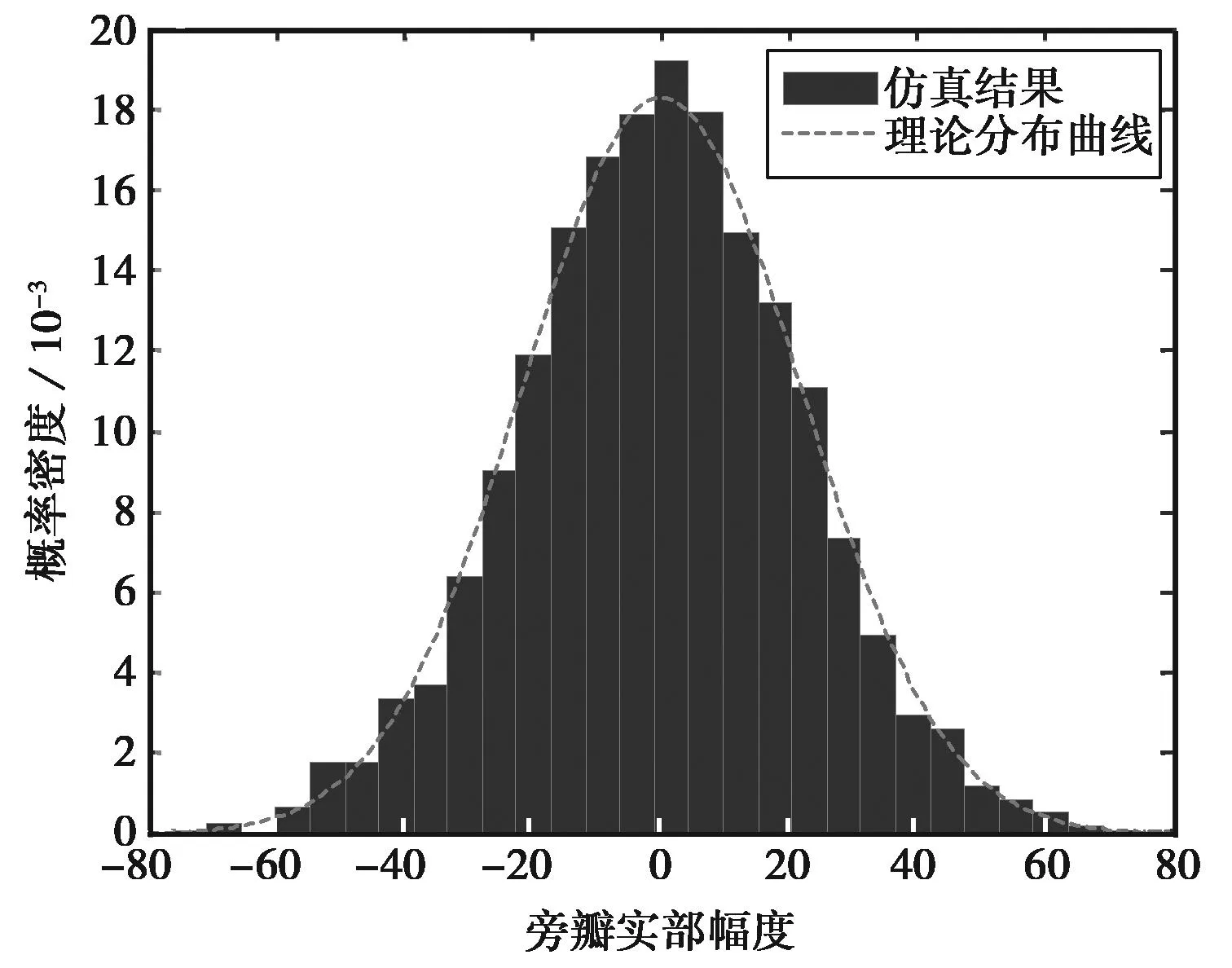
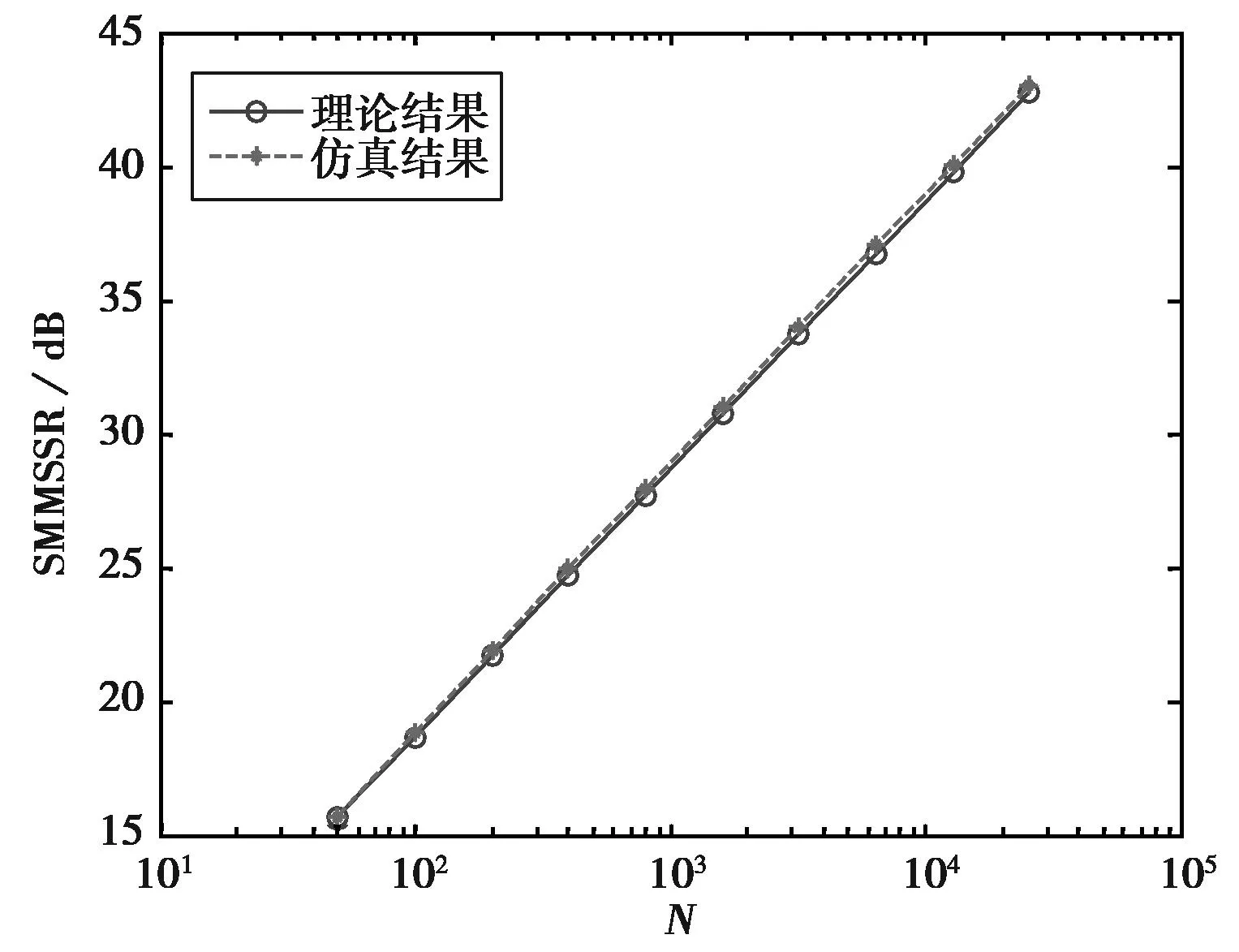
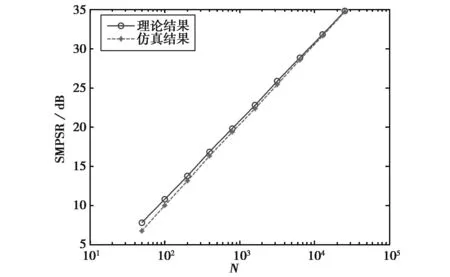
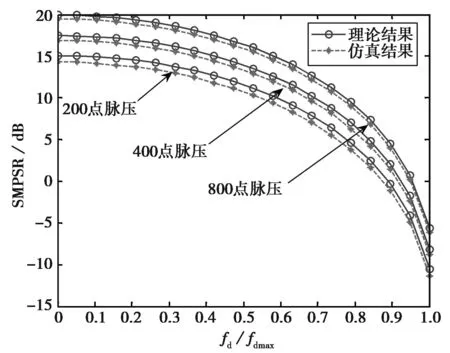
为使信号处理时间内不产生距离门走动,脉压时长和目标速度应满足vrTN

2统计主瓣均方旁瓣比

噪声调相连续波信号是随机过程,对其各指标的性能需从统计层面研究.NPMCWR回波相关输出的均值表达式为

ER(τ)=〈R(τ)〉=ArAcexp[j2π(f0τ-fdTr)]×

jθ(t-Tc)]〉dt.

(10)

令Δt=ξdt+τ-ξdTr,由二变量高斯分布的特征函数可得[13]

〈exp[jθ(ξr(t-Tr))-jθ(t-Tc)]〉

(11)

由于目标速度vr≪c,可认为ξd近似为零,则相关系数ρ(Δt)≈ρ(τ),将式(11)代入式(10),相关输出均值表达式改写为

ER(τ)=ArAcexp[j2π(f0τ-fdTr)]·

(12)

将式(12)进一步求解得

exp[j2π(f0τ-fdTr)]·exp(πfdTN)·

(13)

带限高斯白噪声e(t)的统计功率谱密度(PowerSpectralDensity,PSD)形状为矩形,根据Wiener-Khinchine定理,基带调制噪声e(t)的PSD傅里叶逆变换为其自相关函数,表达式为

(14)

式中: Be(t)是高斯白噪声的带宽; τ为相关延迟.

2) τ≠0,即Tr≠Tc,此时ER(τ)为相关输出统计旁瓣.

噪声调相连续波雷达相关输出的统计均方表达式为

〈|R(τ)|2〉=〈R(τ)R*(τ)〉

〈exp{j[θ(ξr(t1-Tr))-θ(t1-

Tc)-θ(ξr(t2-Tr))+θ(t2-

Tc)]}〉dt1dt2.

(15)

〈exp{j[θ(ξr(t1-Tr))-θ(t1-Tc)-

θ(ξr(t2-Tr))+θ(t2-Tc)]}〉

=〈exp{j[θ1-θ2-θ3+θ4]}〉

ρ23-2)].

(16)

将式(16)代入式(15)得

ρ24+ρ34-ρ14-ρ23-2)]dt1dt2.

(17)

式(17)中的相关系数表达式为:

ρ12=ρ(ξr(t1-Tr)-(t1-Tc))

=ρ(ξdt1+τ-ξdTr);

ρ13=ρ(ξr(t1-Tr)-ξr(t2-Tr))

=ρ(ξr(t1-t2)),

ρ24=ρ((t1-Tc)-(t2-Tc))=ρ(t1-t2);

ρ34=ρ(ξr(t2-Tr)-(t2-Tc))

=ρ(ξdt2+τ-ξdTr);

ρ14=ρ(ξr(t1-Tr)-(t2-Tc))

=ρ(ξrt1-t2+τ-ξdTr);

ρ23=ρ((t1-Tc)-ξr(t2-Tr))

=ρ(t1-ξrt2-τ+ξdTr).

由于目标速度vr≪c,ξr≈1,ξd≈0, 式(17)中相关系数简化为ρ12≈ρ(t),ρ13≈ρ(t1-t2),ρ24≈ρ(t1-t2),ρ34≈ρ(τ),ρ14≈ρ(t1-t2+τ),ρ23≈ρ(t1-t2-τ), 式(17)可改写为

2ρ(t1-t2)-ρ(t1-t2+τ)-

ρ(t1-t2-τ)-2]}dt1dt2.

(18)

ρ(x+τ)-ρ(x-τ)-2)]dxdy+

ρ(x+τ)-ρ(x-τ)-2)]dxdy

ρ(x+τ)-ρ(x-τ)-2)]dx+

ρ(x+τ)-ρ(x-τ)-2)]dx

2ρ(x)-ρ(x+τ)-ρ(x-τ)-

2)]dx.

(19)

雷达数字信号处理的采样间隔为ts,相关延迟τ的延迟单元为1/B,脉压器相关积累时长TN=Nts,令|V(τ)|2=〈|R(τ)|2〉,则相关输出的统计均方表达式(19)的离散形式可写为

|V(τ)|2=〈|R(τ)|2〉

exp[j2πfd(nts)]×

ρ(nts+τ)-ρ(nts-τ)-2]}ts.

(20)

(21)

调相连续波雷达统计均方主旁瓣比RSMMSS表达式可表示为

(22)

式中

2ρ(nts)-ρ(nts+τ)-ρ(nts-τ)-

表示对观测距离门内的脉压输出旁瓣求统计均方值.由式(22)可知,统计均方主旁瓣比和目标回波延迟Tr无关,而与目标多普勒频移fd,相关积累时长TN,有效相移Kpmσn有关.

3统计主瓣峰值旁瓣比

假设目标速度vr≪c,则ξr≈1,将式(12)、式(18)代入脉压输出旁瓣的方差计算中,可得方差表达式为

ρ(t1-t2+τ)-ρ(t1-t2-τ)-2)]-

(23)

令x=t1-t2,y=t2,由Jacobi式|J|=1,对式(23)做二变量代换化简后得

ρ(x+τ)-ρ(x-τ)-2)]-

(24)

参考式(9),接收滤波器相关输出的离散表达式可表示为

R(τ)≈ArAcexp[j2π(f0τ-fdTr)]·

Tr)-e(nts-Tc)]}·ts.

(25)

式中:e(nts-Tr),e(nts-Tc)均为高斯噪声;e(nts-Tr)-e(nts-Tc)仍为高斯噪声.τ≠0时,R(τ)输出为旁瓣,由中心极限定理可知,此时R(τ)的旁瓣是若干独立同分布的随机变量之和,R(τ)的旁瓣概率分布是趋于正态的.

图2中虚线为以旁瓣实部、虚部的均值和方差为参数的正态分布概率密度曲线.可见,R(τ)旁瓣的实部和虚部的概率分布特性均近似服从正态分布.由于是单次实验,且样本容量有限,因此是近似服从正态分布,应允许出现少许偏差.进行1 000次Monte-Carlo实验,得到每次实验旁瓣实部、虚部的均值和方差,再求统计平均,可得旁瓣实部、虚部的统计均值均为0;旁瓣实部的统计方差为22.59、虚部的统计方差为22.56,近似相等.

(a) 旁瓣实部

(b) 旁瓣虚部图2　脉压输出旁瓣的实部、虚部的统计直方图

=a+bj.

(26)

式中实部a和虚部b分别服从标准正态分布,且统计独立,令V=|a+bj|2=a2+b2, 则随机过程V服从自由度为2的χ2分布,V的概率密度为

(27)

R(τ)旁瓣峰值近似服从均匀分布,单个距离门延迟Δτ=1/B,若观测的总距离门数为P,则相关输出旁瓣峰值仅出现在P-1个距离门上,且近似服从均匀分布,其概率密度为1/(P-1),则旁瓣峰值出现的概率密度为

(28)

(29)

当τ≠0时,相关输出旁瓣近似服从正态分布,其均值ER(τ)近似为零,则有峰值旁瓣的能量

(30)

可得统计峰值主旁瓣比RSMPS表达式为

(31)

式中

ρ(x+τ)-ρ(x-τ)-2)]-

由式(31)可知,统计峰值主旁瓣比亦和目标回波延迟Tr无关,而与目标多普勒频移fd,相关积累时长TN,有效相移Kpmσn有关.

4仿真与分析

1) 目标静止,与雷达径向距离10km,观测距离门数P=1 001,脉压点数N=50×2i,其中i=0,1,2,…,9.对SMMSSR和SMPSR随脉压点数的变化进行1 000次Monte-Carlo实验的仿真结果和公式推导的式 (22)、式(31)的理论结果对比如图3所示.

(a) 统计主瓣均方旁瓣比(SMMSSR)

(b) 统计主瓣峰值旁瓣比(SMPSR)图3　SMMSSR和SMPSR与脉压点数N的关系

雷达系统的时宽带宽积为B·Nts=N/2,图3中横坐标表示的脉压点数的一半即为时宽带宽积.当时宽带宽积每增加一倍时,SMMSSR增加3dB左右,SMPSR增加2.5dB左右,其中SMMSSR的仿真结果和理论计算几乎完全重叠,而SMPSR随着脉压点数的增加,仿真结果和理论结果趋于一致.由于旁瓣峰值计算中用到了旁瓣近似高斯分布特性,当脉压点数越少时,该近似分布与高斯分布误差越大,而随着脉压点数的增加,分布越来越接近高斯分布,因而理论结果与仿真结果更加吻合.

2) 200点、400点、800点脉压长度时,分析目标运动产生的多普勒变化对SMMSSR和SMPSR的影响, 1 000次Monte-Carlo实验的仿真结果和根据公式推导的式(22)、式(31)的理论计算结果进行对比.

当TN=1/fd时,脉压时长为目标多普勒周期,相关输出已无法得到峰值.因此仿真中取最大多普勒频移fdmax=0.95/TN,仿真步进为0.05fdmax,200点、400点、800点脉压时长时的理论和仿真如图4所示.

(a) 统计主瓣均方旁瓣比(SMMSSR)

(b) 统计主瓣峰值旁瓣比(SMPSR)图4　同脉压时长SMMSSR和SMPSR与归一化多普勒频率的关系

图4中200点、400点、 800点脉压时SMMSSR和SMPSR的Monte-Carlo仿真结果和公式推导的理论结果平均误差如表1所示.

表1　不同脉压时长时SMMSSR和SMPSR的仿真结果和理论结果的平均误差值

由表1可知,随着脉压点数的增加,SMMSSR的仿真结果和理论结果的平均误差略有增加,而SMPSR的仿真结果和理论结果的平均误差有较明显的改善.整体上SMMSSR误差小于0.3dB,SMPSR误差小于1dB,仿真结果与理论结果能很好地吻合.

对比伪码调相连续波雷达可知[11],目标运动产生的多普勒远小于雷达最大可测多普勒fdmax时,噪声调相连续波雷达对多普勒的敏感性小于伪码调相连续波雷达,而当目标运动产生的多普勒接近雷达最大可测多普勒fdmax时,噪声调相连续波雷达对多普勒的敏感性高于伪码调相连续波雷达.

3) 有效相移Kpmσn对主旁瓣比的影响

噪声调相连续波雷达的脉压时长不变时,Kpmσn取π,2π,4π的SMMSSR和SMPSR见表2.可知增大Kpmσn即增加发射信号带宽,带宽每增加一倍,SMMSSR近似增加3 dB,SMPSR近似增加2.5 dB,且理论和仿真基本吻合.

表2　不同Kpmσn积时SMMSSR和SMPSR的仿真结果和理论值

4)BT积对主旁瓣比的影响

假设目标静止,与雷达径向距离为10 km, 发射信号带宽与脉压时长之积即BT保持不变,其值为200时,有效相移Kpmσn不同时理论和仿真结果如表3所示,表中SMMSSR和SMPSR的理论和仿真值基本一致.且由表3可见噪声调相连续波雷达BT积相同时,输出SMMSSR和SMPSR几乎一致.

表3　BT积不变时SMMSSR和SMPSR的仿真结果和理论值

5结论

本文通过对NPMCWR脉压输出主旁瓣统计规律的研究,推导了噪声调相连续波雷达脉压输出的SMMSSR和SMPSR的数学表达式,为定量分析NPMCWR脉压输出主旁瓣比与脉压长度、多普勒频率、有效相移等参数的关系提供了理论依据.结果表明,SMMSSR和SMPSR均与目标回波延迟Tr无关,而与目标多普勒频移fd、相关积累时长TN、有效相移Kpmσn有关.SMMSSR和SMPSR均与NPMCWR的时宽带宽积BT成线性关系,当BT积不变时,改变相关积累时长TN和有效相移Kpmσn的值,输出主旁瓣比不变.数学表达式的计算结果与Monte-Carlo仿真结果很好地吻合,验证了推导结论的正确性.

参考文献

[1] LIU G, GU H, SU W. Development of random signal radars[J]. IEEE Transactions on Aerospace and Electronic Systems,1999, 35(3): 770-777.

[2] MALANOWSKI M, KULPA K. Detection of moving targets with continuous-wave noise radar: theory and measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(9): 3502-3509.

[3] YANG Jungang, THOMPSON J, HUANG Xiaotao, et al. Random-frequency SAR imaging based on compressed sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(2): 983-994.

[4] LUKIN K A, NARAYANAN R M. Historical overview and current research on noise radar[C]//2011 3rd International Asia-Pacific Conference on Synthetic Aperture Radar (APSAR).Seoul, Sept 26-30, 2011.

[5]张新相,吴铁平,陈天麒. 随机信号雷达抗干扰性能分析[J]. 电波科学学报,2008, 23(1): 189-194.

ZHANG Xinxiang, WU Tieping, CHEN Tianqi. ECCM capabilities of random signal radar[J]. Chinese Journal of Radio Science, 2008, 23(1): 189-194.(in Chinese)

[6] 高许岗,苏卫民,顾红. 随机噪声连续波SAR的性能分析[J]. 电波科学学报, 2010, 25(1): 47-52.

GAO Xugang, SU Weimin, GU Hong. Performance analysis of random noise CW radar[J]. Chinese Journal of Radio Science, 2010, 25(1): 47-52. (in Chinese)

[7] 程院兵, 张卫, 顾红, 等. 噪声连续波雷达脉压输出主旁瓣比推导与分析[J]. 兵工学报, 2012, 33(1): 1-6.

CHENG Yuanbing, ZHANG Wei, GU Hong, et al. Derivation and analysis of mainlobe to sidelobe ratio after pulse compression in noise continuous wave radar[J]. Acta Armamentarii, 2012, 33(1): 1-6. (in Chinese)

[8] 翁晓明, 顾红, 苏卫民. 噪声调频连续波的统计主旁瓣比[J]. 兵工学报, 2014, 35(4): 448-453.

WENG Xiaoming, GU Hong, SU Weimin. Statistical main lobe-to-sidelobe ratio of noise frequency modulated continuous wave[J]. Acta Armamentarii, 2014, 35(4): 448-453. (in Chinese)

[9] AXELSSON S R J. Noise radar using random phase and frequency modulation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(11): 2370-2384.

[10]武昕,李澍,刘畅,等. 基于特征参数的随机噪声雷达相关输出研究[J]. 电波科学学报, 2012, 27(3): 543-550.

WU Xin, LI Shu, LIU Chang, et al. Correlation output of random noise radar based on characteristic parameters[J]. Chinese Journal of Radio Science, 2012, 27(3): 543-550. (in Chinese)

[11]陈金立,顾红,苏卫民. 伪码调相连续波雷达的脉压主旁瓣比数学分析[J]. 兵工学报, 2008, 29(10): 1203-1209.

CHENG Jinli, GU Hong, SU Weimin. Mathematics analysis of main-to-sidelobe ratio after the pulse compression in pseudorandom code phase modulation continuous wave radar[J]. Acta Armamentarii, 2008, 29(10): 1203-1209. (in Chinese)

[12]赵国庆. 雷达对抗原理[M]. 西安: 西安电子科技大学出版社, 2003: 152-154.

[13]PROAKIS J G. 数字通信[M]. 张力军,译. 4版. 北京: 电子工业出版社, 2005: 35-36.

[14]杨国裕. 正态噪声调频雷达信号分析[J]. 南京理工大学学报:自然科学版, 1993, 17(4): 92-96.

YANG Guoyu. Analysis of FM radar signal by normal noise[J]. Journal of Nanjing University of Science and Technology, 1993, 17(4): 92-96. (in Chinese)

吕婧(1984-),女,江苏人,南京理工大学电子工程与光电技术学院博士研究生,研究方向为随机噪声雷达信号处理.

顾红(1967-),男,江苏人,南京理工大学教授,博导,主要研究方向为噪声雷达和稀疏阵列信号处理.

苏卫民(1959-),男,江苏人,南京理工大学教授,博导,主要研究方向为阵列信号处理和雷达成像.

卢广阔, 魏平, 甘露, 等.通信信号的单通道盲分离和码元序列盲估计[J]. 电波科学学报,2015,30(6):1057-1063. doi: 10.13443/j.cjors. 2014121702

LU Guangkuo, WEI Ping, GAN Lu, et al. Single-channel blind signal separation and blind estimation of symbol sequences of communication signals [J]. Chinese Journal of Radio Science,2015,30(6):1057-1063. (in Chinese). doi: 10.13443/j.cjors. 2014121702

Derivation and analysis of statistical mainlobe to sidelobe ratio

of the noise phase modulated continuous wave radar

LÜ JingGU HongSU WeiminBO Chao

(ResearchCenterofElectronicEngineeringTechnology,NanjingUniversityof

ScienceandTechnology,Nanjing210094,China)

AbstractThe sidelobes of pulse compression of noise phase modulated continuous wave radar (NPMCWR) are shown as a noise floor with random characteristic. The mathematical expressions of statistical mainlobe to mean square sidelobe ratio(SMMSSR) and statistical mainlobe to peak sidelobe ratio (SMPSR) are deduced. The relationships between the mainlobe to sidelobe ratio and some parameters such as pulse compression length, Doppler frequency and effective phase shift are analyzed. The results calculated by the mathematical expressions are close to the Monte-Carlo simulation results so that verify the correction of the deduction results.

Key wordsnoise phase modulated continuous wave; pulse compression; mainlobe to sidelobe ratio; noise radar; Doppler

作者简介

收稿日期：2014-10-19

中图分类号TN957

文献标志码A

文章编号1005-0388(2015)06-1048-09