姿态测量误差对星载合成孔径雷达成像质量影响

王伟杰　李春升　杨威　王鹏波　陈杰

(北京航空航天大学 电子信息工程学院,北京 100191)



姿态测量误差对星载合成孔径雷达成像质量影响

王伟杰李春升杨威王鹏波陈杰

(北京航空航天大学 电子信息工程学院,北京 100191)

摘要针对高分辨率条件下卫星弯曲轨迹与姿态测量误差耦合对成像质量的影响开展分析.首先结合高分辨率星载滑动聚束合成孔径雷达(Synthetic Aperture Radar, SAR)成像特点,解析回波信号的空-时-频特性,分析姿态测量误差对回波信号空-时-频特性的影响,构建该影响与成像质量之间的数学映射关系.然后基于高次相位补偿的三步成像算法分析误差所引入的高次补偿相位误差,并给出是否需要进行高次相位补偿的误差临界值.最后,通过计算机仿真验证理论分析的正确性.

关键词星载滑动聚束SAR;姿态测量误差;多普勒中心频率误差;高次相位补偿;成像算法

联系人： 杨威 E-mail：yangweigigi@sina.com

引言

高分辨率是星载合成孔径雷达(Synthetic Aperture Radar, SAR)永恒的追求目标和发展方向[1-2]．滑动聚束成像模式是一种高分辨率宽覆盖的成像模式,能够获得比同等条件条带SAR更高的分辨率、聚束SAR更大的成像面积.国外先进的SAR系统,如PAMIR[3-4],TerraSAR-X[5]都采用了滑动聚束成像模式.

星载滑动聚束SAR成像需要良好的成像参数保证,尤其是多普勒参数,多普勒参数估计是SAR成像处理中必不可少的步骤[6-7].良好的姿态控制和测量精度有利于获得高精度的多普勒参数.卫星姿态是指卫星运行过程中的三轴控制状态,通常采用三轴姿态角——偏航角、俯仰角和滚动角表示.卫星姿态测量精度是通过三轴姿态角的精度来描述的.姿态测量误差[8](Attitude Measurement Error,AME)使多普勒参数估算不准确,影响到定位和聚焦,导致噪声和模糊度的增高,严重时还会影响到图像质量[9].分辨率的不断提高对姿态测量精度提出了越来越高的要求.

SAR系统在设计时,尽量将多普勒中心频率(Doppler Centroid, DC)最小化,避免出现多普勒模糊,现有系统通过控制偏航角使多普勒中心频率最小化[10-12].TerraSAR-X[5]采用德宇航开发的一种全零多普勒指向方法[13],通过同时控制姿态偏航角和俯仰角,能够在理论上将DC减小至0.实际中由于AME的存在会引入多普勒中心频率误差(Doppler Centroid Error, DCE),TerraSAR-X三轴姿态误差能够控制在0.01°以内,存在最大125 Hz的DCE.成像处理虽可以通过杂波锁定自动确定DC以减小DCE,但其估计精度对场景的散射特性有很大依赖性,均匀场景估计精度高,起伏大的区域估计精度低[14],而且要达到较高的估计精度,计算量较大,难以满足实时成像处理的要求.AME引入的DCE,而DCE对高分辨率星载SAR成像质量产生影响,因而定量分析AME-DCE-成像质量之间的相互影响关系是有意义的:一方面能够在一定程度上指导工程设计,对参数设计提出进一步要求;另一方面能够据此提出对成像处理方法的改进,实现成像质量的提升.

1三轴姿态角对DC的影响分析

图1　三轴姿态角示意图

根据文献[16-17],多普勒中心频率与卫星三轴姿态角之间的关系为

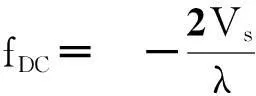
sinγ0cosψ0sinδycosδr-sinγ0sinψ0cosδycosδr)+cos(i)[-cosγ0sinδpcosδr+

sinγ0cosψ0(sinδysinδpsinδr+cosδycosδp)-sinγ0sinψ0(cosδysinδpsinδr-

cosδysinδp)-sinψ0(cosδycosδpsinδr+sinδysinδp)]}

(1)

式中: Vs为卫星飞行速度; λ为波长; γ0为卫星视角; ψ0为方位斜视角; ωe为地球角速度; ωs为卫星角速度； i为轨道倾角； a为轨道半长轴.从式(1)可以看出,卫星姿态对多普勒中心频率的影响十分复杂,对正侧视模式,偏航角和俯仰角测量误差的影响远大于滚动角.偏航角和俯仰角误差的存在使波束指向不准,影响波束中心照射到目标的时刻及该时刻卫星与目标的相对位置.AME与成像质量之间不存在直接的对应关系,中间存在DCE的过渡,故在以下的分析中先通过式(1)计算AME所引入的DCE,再分析DCE对成像质量的影响,间接建立AME与成像质量之间的影响关系.

2DCE对成像处理的影响分析

2.1　三步成像算法中的高次相位补偿

三步成像算法(Three-stepFocusingAlgorithm,TSFA)[15]解决了传统算法处理星载滑动聚束数据方位向频谱混叠和图像域混叠的问题,降低了对脉冲重复频率(PulseRecurrenceFrequency,PRF)的要求,其采用的斜距模型为等效斜视模型(EquivalentStrabismusModel,ESM),斜距拟合误差小于正侧视模型和二次逼近模型[14].载荷与点目标之间斜距R1(t;Rref)为

Vtcosφref]1/2.

(2)

式中： t为方位向“慢时间”； Rref为中心时刻载荷相对场景中心的参考斜距； V为等效速度； φref为参考等效斜视角.

ESM将卫星轨迹视为直线R1(t; Rref),而实际轨迹R3(t)为曲线,对合成孔径时间较短的SAR工作模式二者偏离很小,不需要进行高次相位补偿(High-orderPhaseCompensation,HOPC),对成像处理的影响可以忽略;但对合成孔径时间较长的高分辨率星载滑动聚束SAR,R1(t;Rref)与R3(t)偏离较大,需要将二者之差ΔR31(t;Rref)对应的高次相位补偿掉,否则将引入较大的高次相位误差.分别将R1(t;Rref)和R3(t)在t=0按式(3)的形式进行泰勒级数展开,R3(t)随时间的变化规律根据仿真或真实星历参数获得,其各次项系数通过对R3(t)曲线拟合得到.

(3)

式(3): f3表示多普勒三次频率; f4表示多普勒四次频率.

ΔR31(t;Rref)常数项、一次项和二次项均为0,仅存留三次及三次以上的高次项.ΔR31(t;Rref)对应的高次补偿相位表达式为

(4)

2.2　DCE对ESM的影响

AME引入DCE,对ESM的影响主要体现在对参考等效斜视角φref的反演上,引入了误差Δφref,进而引入了斜距误差、相位误差.

ESM中多普勒中心频率fD(Rref)和多普勒中心调频率fR(Rref)计算式如下所示:

(5)

(6)

可得Vref和φref的反演式为:

(7)

(8)

(9)

正侧视情况下sinφref≈1,Δφref较小,sinφref值基本不变,从式(9)可以得出Δφref与ΔfD(Rref)成近似线性关系.

DCE对ESM的影响如图2所示.Δφref使ESM相对无误差实线L发生微小倾斜,如虚实线L′所示.图中虚线l为卫星真实轨迹,N为场景中心,O为波束等效旋转点,r0为参考斜距,r1为等效旋转点到场景中心的斜距.单纯考虑DCE的影响,L′与L相交于B点.B点为L中心时刻,卫星从A至C对N进行一个完整合成孔径时间的照射.当DCE存在时,“认为”L上A、B、C三点多普勒频率在L′上A′、B′、C′点处即可达到,B′成为新的多普勒中心位置.进行成像处理后,N不再位于图像中心,SAR图像在方位向上发生偏移.

图2　多普勒中心频率误差对等效斜视模型的影响示意图

存在DCE时ESM斜距表达式如(10)所示,其引入的斜距误差如式(11)所示.

Δφref)]1/2.

(10)

ΔR21(t;Rref)=R2(t;Rref)-R1(t;Rref)

(11)

将式(9)代入(11)可得式(12):

(12)

(13)

从式(13)可以看出:斜距误差ΔR21(t;Rref)主要成分为t的一次项,引起目标成像位置偏移;此外还包含t的二次项,在较高分辨率正侧视条件下该项引入的调频率误差很小不会影响聚焦,但对更高分辨率、大斜视情况该项可能会影响聚焦效果.由于R1(t;Rref)包含t的各次项成分且在公式简化过程中用到了近似,ΔR21(t;Rref)实际还包含了相当程度的时间t高次分量.该高次分量在不进行HOPC时对成像质量无影响,对成像造成影响的是固定的式(4)中高次相位ΔΦ(t;Rref),其值不随DCE大小而改变;而在进行HOPC时,该高次分量在ΔΦ(t;Rref)被补偿的基础上成为了新的高次相位误差ΔΦerror,出现“过补偿”的现象;在某些情况下,ΔΦerror绝对值甚至大于ΔΦ(t;Rref)绝对值,进行HOPC的成像质量反而不如不进行HOPC,这将在下一节进行讨论.

2.3　DCE对高次相位补偿的影响

无DCE情况下HOPC体现在图3为补偿同一时刻真实轨迹l与ESML到场景中心的斜距差所对应的延时相位.DCE存在时,ESM发生小角度倾斜,HOPC体现的是补偿同一时刻真实轨迹l与误差ESML′之间的斜距差所对应的延时相位,相对无误差情况,HOPC除补偿了ΔΦ(t;Rref)外,还额外引 入了-ΔR21(t;Rref)对应延时相位的高次分量ΔΦerror.HOPC三次、四次补偿相位如式(14)、(15)所示,其中T为合成孔径时间.

(14)

(15)

三次、四次补偿系数Δf3、Δf4的计算式如(16)、(17)所示：

Δf3=f30-f3；

(16)

Δf4=f40-f4.

(17)

式中,f30、f40为真实斜距时间序列按式(3)展开的三次、四次项系数.

高次项系数f3、f4的计算与φref有关,如式(18)、(19)所示：

(18)

(19)

Δφref对f3、f4的计算引入误差,先分析Δφref对sinφref和cosφref的影响:

sin(φref+Δφref)=sinφrefcos Δφref+

cosφrefsin Δφref≈sinφref;

(20)

cos(φref+Δφref)=cosφrefcos Δφref-sinφrefsin Δφref

≈cosφref-Δφrefsinφref.

(21)

(22)

(23)

(24)

(25)

将式(24)、(25)代入式(14)、(15)可得DCE对HOPC所引入的三次、四次相位误差如式(26)、(27)所示:

(26)

(27)

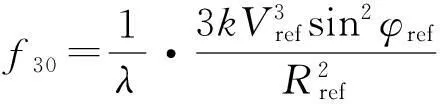
(28)

令|ΔΦ3error|≥|ΔΦ3|得

(29)

若三次相位在高次相位中占主导地位,当满足式(29)条件时,不进行HOPC将比进行HOPC取得更好的成像结果.同理若四次相位占主导地位,可据式(27)和(15)分析.

2.4　对定位精度的影响

DCE引起回波信号方位向频谱偏移,影响目标最终聚焦位置,使SAR图像在方位向发生偏移.滑动聚束模式目标成像位置偏移量与条带模式不同,其计算式为

(30)

式中,A为混合度因子,A=r1/(r1+r0).

此外,频谱偏移使频谱相对加权窗不对称,也会影响成像质量.

3仿真结果分析

仿真中部分参数如表1所示.

按表1和式(29)计算DCE临界值为217Hz,下面分别分析DCE为0、120Hz、217Hz和310Hz时对成像质量的影响.对场景中心点目标,不同DCE下所引入的三次补偿相位误差ΔΦ3error、四次补偿相位误差ΔΦ4error如图3(a)、3(b)所示.

表1　仿真参数

(a) 三次相位误差

(b) 四次相位误差图3　不同DCE下对HOPC所引入的补偿相位误差

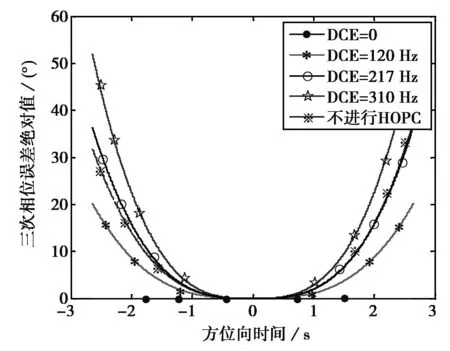
从图3(a)可以看出三次相位误差较大，其随着DCE增加而变大；从图3(b)可以看出四次相位误差很小，更高次项的相位误差可以忽略，因而高次相位误差主要体现为三次相位误差.DCE存在时，实际取暴利偿的三次相位为(ΔΦ3+ΔΦ3error)，如图4(a)所示，|ΔΦ3error|与|ΔΦ3|的比较如图4(b)所示.

在图4(a)中,—·—实线为需要补偿的三次相位,存在DCE时,实际补偿的三次相位与该曲线偏离.当DCE在临界值附近时,实际补偿的三次相位接近0,与没有进行HOPC的效果相当.从图4(b)可以看出,当DCE等于临界值时|ΔΦ3error|与|ΔΦ3|曲线基本重合,进行HOPC与不进行HOPC的三次相位误差基本相等;当DCE小于临界值时,前者小于后者,进行HOPC三次相位误差更小;当DCE大于临界值时,前者大于后者,不进行HOPC三次相位误差更小.

(a)

(b)图4　DCE存在时实际补偿的三次相位

场景中心点目标方位向成像结果如表2所示.

表2　方位向成像结果对比

从表2可以看出,在不进行HOPC时,不同DCE对点目标成像质量影响不大,因为此时三次相位误差为固定的ΔΦ3.进行HOPC时,成像质量随DCE增加而下降,DCE存在临界值217Hz,此时进行HOPC与不进行HOPC成像质量基本相同,当DCE小于217Hz时,进行HOPC成像质量更优,当DCE大于217Hz时,不进行HOPC成像质量更优.仿真结果与理论分析一致.

表2对应成像结果的方位向剖面图及二维剖面图如表3所示.

表3　成像结果剖面图对比

4结论

姿态测量误差会引入多普勒中心频率误差.多普勒中心频率误差使等效斜视模型产生小角度的倾斜,进而产生斜距误差.该斜距误差对应的延时相位经分解后主要成分为方位时间的一次项,还包含二次项和高次项成分——其中一次项成分引起目标成像位置的偏移;二次项成分可能影响高分辨率、大斜视模式的成像聚焦效果;高次项成分对星载滑动聚束SAR高次相位补偿操作引入高次补偿相位误差,从而影响成像质量.存在多普勒频率误差的临界值,在多普勒中心频率误差大于该临界值的情况下不进行高次相位补偿成像质量更好,小于该临界值时进行高次相位补偿成像质量更好.本文分析了姿态测量误差对多普勒中心频率的影响,进而分析了多普勒中心频率误差对高分辨率星载SAR三步成像处理算法的影响,主要分析了多普勒中心频率误差对成像处理所引入的高次相位误差,并给出了其临界值,最后通过仿真实验验证了理论分析的正确性,对工程设计有一定的指导意义.

参考文献

[1]杨威,李春升,陈杰,等. 时钟同步对星载多通道合成孔径雷达成像影响[J].电波科学学报,2011,26(4):636-640.

YANGWei,LIChunsheng,CHENJie,etal.Effectsoftimesynchronizationonimagequalityofspacebornemulti-channelsSAR[J].ChineseJournalofRadioScience, 2011, 26(4): 636-640. (inChinese)

[2]黄海风,董臻,梁甸农. 星载双站SAR“停走停”假设误差分析[J]. 电波科学学报,2006,21(6):863-867+878.

HUANGHaifeng,DONGZhen,LIANGDiannong.Erroranalysisof“stopandgo”hypothesisofspacebornebistaticSAR[J].ChineseJournalofRadioScience, 2006, 21(6): 863-867+878. (inChinese)

[3]ENDERJHG,BRENNERAR.PAMIR:-awidebandphasedarraySAR/MTIsystem[C]//IEEProceedingsRadar,SonarandNavigation, 2003, 150(3): 165-172.

[4]ENDERJHG,BERENSP,BrennerAR,etal.MultichannelSAR/MTIsystemdevelopmentatFGAN:FromAERtoPAMIR[C]//IEEEGeoscienceandRemoteSensingSymposium, 2002, 3: 1697-1701.

[5]MITTERMAYERJ,LORDR,BORNERE.SlidingspotlightSARprocessingforTerraSAR-Xusinganewformulationoftheextendedchirpscalingalgorithm[C]//ProceedingsofIGARSS.Toulouse, 2003: 1462-1464.

[6]OLIVERC,QUEGANS.UnderstandingSyntheticApertureRadarImages[M].Norwood:ArtechHouse,MA, 1988.

[7]CURLANDERJ,MCDONOUGHR.SyntheticApertureRadar:SystemsandSignalProcessing[M].NewYork:JohnWiley&Sons,1991.

[8] 匡辉,陈杰,杨威,等. 多通道星载合成孔径雷达姿态误差影响分析与补偿[J]. 电波科学学报,2014,29(6):1070-1075.

KUANGHui,CHENJie,YANGWei,etal.Analysisandcompensationfortheattitudeerrorofmulti-channelspace-bornesyntheticapertureradar[J].ChineseJournalofRadioScience, 2014,29(6):1070-1075. (inChinese)

[9]BENNETTJR,CUMMINGIG.AdigitalprocessorforproductionofSEASATsyntheticapertureradarimagery[C]//ProcSURGEWorkshopFrascati,July16-18, 1979.

[10]RUNGEH.BenefitsofantennayawsteeringforSAR[C]//ProcIGARSS, 1991,1: 257-261.

[11]CHANGCY,CURLANDERJC.Attitudesteeringforspaceshuttlebasedsyntheticradars[C]//Proc.IGARSS,1992，1: 297-301.

[12]ELDHUSETK.AccurateattitudeestimationusingERS-1SARrawdata[J].InternationalJournalofRemoteSensing, 1996, 17(14): 2827-2844.

[13]FIEDLERH,BOERNERE,MITTERMAYERJ,etal.TotalzeroDopplersteering-anewmethodforminimizingtheDopplercentroid[J].IEEEGeoscienceandRemoteSensingLetters, 2005, 2(2): 141-145.

[14]钟铨. 合成孔径雷达卫星[M]. 北京:科学出版社,2001.

[15]杨威,李春升,陈杰,等. 星载SAR滑动聚束模式三步扩展算法[J]. 北京航空航天大学学报,2012,27(3):297-302.

YANGWei,LIChunsheng,CHENJie,etal.Extendedthree-stepfocusingalgorithmforspaceborneslidingspotlightSARimageformation[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2012, 27(3): 297-302. (inChinese)

[16]HARDIERC,HAYATMM,ARMSTRONGE,etal.Scene-basednonuniformitycorrectionusingvideosequencesandregistration[J].OSAAppliedOptics, 2000, 39: 1241-1250.

[17]刘光炎,林幼权. 星载SAR成像对卫星姿态控制精度的要求[J]. 中国电子科学研究院学报,2007,2(2): 109-114+122.

LIUGuangyan,LINYouquan.ThedemandofsatelliteattitudecontrolinspaceborneSARimaging[J].JournalofChinaAcademyofElectronicsandInformationTechnology, 2007,2(2): 109-114+122. (inChinese)

王伟杰(1988-),男,山东人,北京航空航天大学电子信息工程学院博士研究生,研究方向为高分辨率星载SAR信号仿真与成像.

李春升(1963-),男,天津人,北京航空航天大学电子信息工程学院教授、博士生导师,研究方向主要包括星载SAR系统总体与仿真、多源遥感图像信息融合、信息获取与处理等.

杨威(1983-),男,湖北人,北京航空航天大学电子信息工程学院讲师,研究方向为高分辨率星载SAR信号仿真与成像技术、新体制雷达技术等.

王鹏波(1979-)，男，江西人，北京航空航天大学，讲师，博士，主要从事新体制成像雷达系统技术、高分辨率雷达成像处理以及数字图像处理等方面的研究工作.

陈杰(1973-)，男，教授、博士生导师，长期从事高分辨率微波遥感信息系统理论与方法研究.2005 年获得北京市高等教育成果二等奖，2006 年入选教育部"新世纪优秀人才支持计划"，2008 年获霍英东教育基金会第十一届高等院校青年教师奖三等奖.承担国家自然科学基金、“973”计划、“863”计划、国家重大专项等多项课题.已发表论文100 余篇，其中SCI(E)检索15 篇，EI检索80 余篇.申请国家发明专利20 余项，合作编写教材4 部，合作出版译著1 部.

吕婧, 顾红, 苏卫民, 等. 噪声调相连续波雷达统计主旁瓣比推导和分析[J].电波科学学报,2015,30(6):1048-1056. doi:10.13443/j.cjors. 2014101901

LYU Jing, GU Hong, SU Weimin, et al. Derivation and analysis of statistical mainlobe to sidelobe ratio of the noise phase modulated continuous wave radar[J]. Chinese Journal of Radio Science,2015,30(6):1048-1056. (in Chinese). doi:10.13443/j.cjors. 2014101901

Attitude measurement error effect on imaging

quality of spaceborne SAR

WANG WeijieLI ChunshengYANG WeiWANG PengboCHEN Jie

(SchoolofElectronicsandInformationEngineering,BeihangUniversity,Beijing100191,China)

AbstractUnder high resolution condition, the effect of coupling between satellite curved orbit and attitude measurement error on imaging quality was studied. Firstly, combined with imaging characteristic of high resolution spaceborne sliding spotlight synthetic aperture radar (SAR), the space-time-frequency property of echo signal was analyzed and attitude measurement error effect on it was discussed. Mapping relationship between attitude measurement error and imaging quality was also given. Then based on three-step focusing algorithm combined with high-order phase compensation procedure, the high-order compensating phase error was analyzed. The critical value of error was brought forward as to whether or not to employ high-order phase compensation could get better imaging quality. Finally, computer simulation results identify the validity of theoretical analysis.

Key wordsspaceborne sliding spotlight SAR; attitude measurement error; Doppler centroid error; high-order phase compensation; imaging algorithm

作者简介

收稿日期：2014-12-14

中图分类号TN957

文献标志码A

文章编号1005-0388(2015)06-1039-09