不同海域多波段小擦地角海面散射特性的影响因素分析

吴涛　令狐龙翔　吴振森　苏翔　孙天齐

(1.西安电子科技大学物理与光电工程学院,西安 710071;2.中国海洋大学,青岛 266071)



不同海域多波段小擦地角海面散射特性的影响因素分析

吴涛1令狐龙翔1吴振森1苏翔1孙天齐2

(1.西安电子科技大学物理与光电工程学院,西安 710071;2.中国海洋大学,青岛 266071)

摘要根据东南沿海和西太平洋海面温度场与盐度场卫星数据,利用双Debye模型以及含泡沫的M-G模型计算等效介电常数．分析表明:不同海域温度与盐度变化对P/L波段介电常数虚部的影响大于实部,其他频段影响略小;但介电常数对给定频率的海面散射系数影响只在0.1 dB左右,故主要影响仍来自于不同海域的海情海况．基于修正双尺度法和矢量辐射传输理论,提出了多尺度海面电磁散射的含泡沫修正双尺度方法,考虑实际海面海况与不同频率的截断波数,数值计算了不同波段(即P、L、S、X、Ku波段)频率海面后向散射系数随风速风向、波高、泡沫覆盖率、频率与极化等影响因素的变化情况,总结分析了基于多尺度海面小擦地角电磁散射机理．

关键词小擦地角;多波段;修正双尺度;海面后向电磁散射

资助项目: 国家自然科学基金(No.61172031)

联系人： 吴涛 E-mail: twu@stu.xidian.edu.cn; 吴振森 E-mail: wuzs@mail.xidian.edu.cn

引言

小擦地角下海面电磁散射强度比理论计算要强很多,情形也更复杂,对小擦地角散射的研究有利于促进雷达探测、海杂波研究及目标识别的研究进展．国外对小擦地角下的海面雷达回波做了很多实验及理论研究,美国海军实验室[1]在1971年左右获得的超高频(Ultrahigh Frequency, UHF)、L、C和X波段的机载4FR测量是第一次在很宽频率范围内真正全面收集的海杂波数据,是本文重要的参考;1990年Henry等人[2]利用设置在那慕尔岛上的L/S/C波段雷达实验实现了测量极低擦地角(<0.2°)的后向散射,丰富了极小擦地角下数据;1994年Ngo与Rino[3]提出波束模拟计算擦地角下粗糙面散射,可以数值分析擦地角10°时1 000λ大的粗糙表面．2008年Paul等人[4]以经验研究为基础,考虑破碎波及白冠对小擦地角下雷达后向散射的影响,得出水平极化强度在破碎浪时增强了10～15 dB,而垂直极化变化仅1～2 dB左右,也作为本文研究验证．2009年Naheed[5]在小尺度考虑二阶散射效应扩展Bragg复合海面理论,使之适用小擦地角(>5°)情况,由此修正双尺度法计算风速7 m/s与15 m/s下L/C/Ku波段后向散射,得出高海情下HH极化强度增大8 dB,同时Ku波段结果也较好地符合实验结果．

我国对擦地角海面电磁散射也做了很多研究,1994年复旦大学的金亚秋[6]利用矢量辐射传输方法计算海面均匀泡沫覆盖的后向散射系数,但没有给出小擦地角情形,其研究对本文有指导意义．2002年张延东等[13]提出海面分形海谱,并应用修正双尺度分析小擦地角下海面散射回波及振幅特性,2009年张金鹏、吴振森等[7]进一步提出了四修正双尺度模型,结合海面泡沫的矢量辐射传输模型计算电磁散射,本文在此基础上引入截断波数对小擦地下海面散射特性进行详细分析．2013年罗根、张民[8]等着重考虑HH极化下的多普勒效应和强散射问题,并引入中尺度破碎波模型处理海尖峰使本文有所参照．

本文首先根据海面温度场与盐度场数据计算不同温度、盐度下多波段的介电常数,并利用混合介质模型修正海水介电常数,同时考虑实际海面海况与不同频率的截断波数,据此研究对小擦地角范围为0～15°下的海面同极化电磁散射系数的影响因素．

本文采用的时谐因子为e-iωt,其中ω为角频率．

1不同海域介电常数模型

2004年Meissner和Wentz[9]提出双Debye海水介电常数模型,在本文讨论的P波段到Ku波段频率内十分适用,计算公式为

ε(T,S)=ε∞+(εs(T,S)-ε1(T,S))/

(1)

式中: T表示温度,℃; S表示盐度,‰; f是入射电磁波的频率,GHz; fn=1,2(T,S)表示第一、二类Debye相关频率,GHz; σ是海水的电导率; ε∞是频率无限大时的介电常数; εs(T,S)是静态介电常数; ε1(T,S)代表中间频率介电常数;其中ε∞、εs(T,S)及ε1(T,S)均是与温度、盐度相关的函数; ε0=8.854×10-12F/m是自由空间的介电常数．

风驱海面水下富含空气泡,而空气与海水介电常数相差较大,因此我们利用混合介质模型修正海水介电常数,本文采用Maxwell-Garnett模型[10],即

(2)

分析中国海洋大学提供的2007-2011年东南沿海和西太平洋海面温度场与盐度场卫星数据,东海、黄海海水温度随季节变化明显,范围跨度5～30℃,南海、西太平洋温度变化平缓,约25℃;而各海域盐度区域变化平缓(约1‰),范围跨度30‰～35‰．表1是2013年8月不同海域对应的平均温度、盐度．

表1　2013年8月不同海域平均温度、盐度

由图1～2可以看出:温度与盐度范围变化主要对P/L波段介电常数的虚部有较大影响;其他波段海面(尤其X/Ku)介电常数对温度和盐度变化不敏感,特别是盐度对介电常数实部的影响极小,其主要影响来自于温度变化．

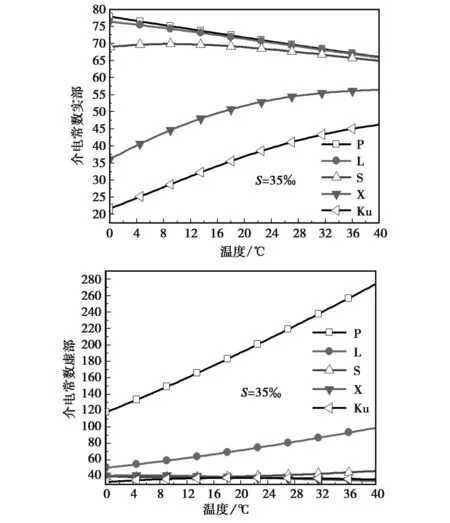
图1　不同波段介电常数随温度变化曲线

图2　不同波段介电常数随盐度变化曲线

2含泡沫的修正双尺度海面散射

吴振森、张金鹏等[7]完善了修正双尺度模型,使其适用于计算平面波入射下小擦地角海面后向散射系数,其公式为

(1+zxtanθi)P(zx,zy)dzxdzy．

(3)

传统双尺度方法只能计算擦地角20°,而修正双尺度法可以计算擦地角小于5°的海面电磁散射,本文基于修正双尺度引入更符合实际海面的泡沫白冠覆盖,则更具有实际意义．

早期双尺度方法只是简单基于电磁波波数,对所有海况,取一定值截断波数kcut,选择范围一般为ki/1.5～ki/40,缺乏针对性的变化．实际上截断波数应随入射电磁波频率和海况的主要指标风速而产生变化．我们结合不同海况下海面复合模型中针对大尺度波和小尺度波各分量模型的适用条件,给出了适用于不同风速和频率下的截断频率选择准则,针对不同的海况计算出合适的截断波数kcut．

复合表面模型中针对大小尺度波分量模型的成立条件分别为:

(4)

式中: ki是入射电磁波数,GHz; θi是入射角度; σc是海面平均曲率的标准离差； δs为小尺度波面的均方根高度,且有:

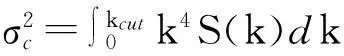
(5)

(6)

式中: S(k)为海谱函数,根据不同的海谱,可取不同的函数形式．

令式(4)中2πσc/ki和kiδscos(θi)具有相同的远小于1的限制值kcut,即

(7)

据此可得图3所示多波段下不同海况的截断波数．可以看出:在风速小于6m/s的中低海情,截断波数只与频率相关为一定值;随风速增加低频段(P/L/S)截断波数不变,仍在0～10rad/m之间,而高频段(X/Ku)截断波数随之增加,X截断波数变化范围为30～35rad/m,Ku截断波数为44～70rad/m,即此时海面海况对多尺度海面的形成有很大影响;同时可以看出随着频率的增大,同一风速下截断波数也随着增大．

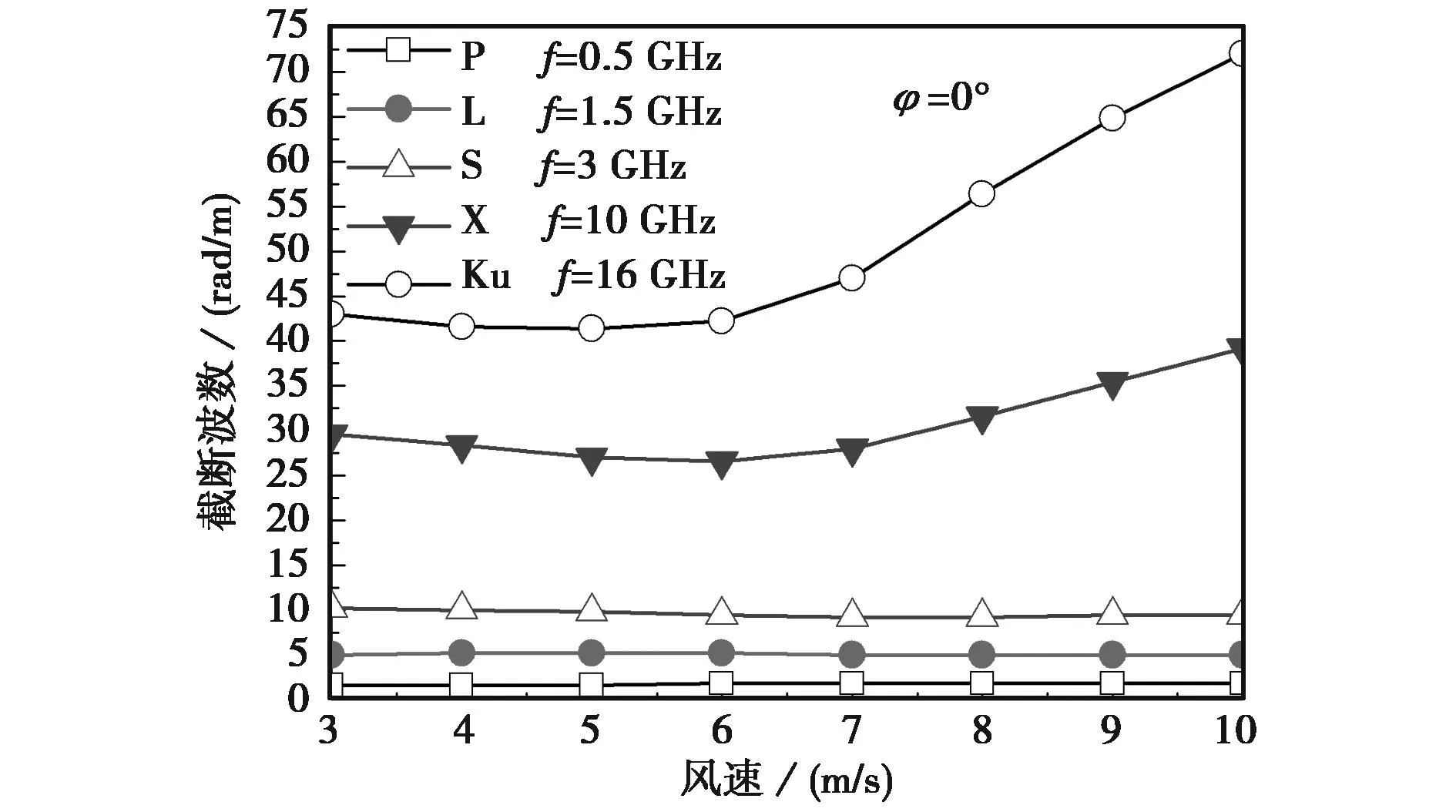
图3　不同波段不同海况下截断波数变化

实际海面泡沫随机覆盖,简便起见认为是均匀部分覆盖,其覆盖率可采用中国海洋大学提供的拟合白冠覆盖率经验曲线得到的公式:

(8)

参考文献本文泡沫模型为平均厚度4 cm,平均半径0.39 mm,单位体积个数106的泡沫层．[7],利用矢量辐射传输方程(Vector Radiative Transfer Method, VRT)得到包含一阶解的海面后向散射系数为:

(9)

(10)

(11)

式中： ke,ks分别为单个泡沫粒子的消光系数及散射系数； Rh0,Rv0分别为水平和垂直极化菲涅耳反射系数； σpq0(θi)是无泡沫层时粗糙海面的后向散射系数; 因子e-2κedsec θi是电磁波经过厚度为d的泡沫粒子层时散射和吸收的衰减因子．

对于海面泡沫均匀部分覆盖模型,计算公式采用有无泡沫海面的散射叠加,即

σpp(θi)=(1-Cw)σpp0(θi)+Cw×

(12)

式中: Cw为白浪覆盖率; σpp0(θi)为根据四修正双尺度法计算出的未被泡沫覆盖的海面后向散射系数(pp表示同极化)．

3小擦地角海面散射系数影响因素

利用前文含泡沫海面修正双尺度方法,研究小擦地角范围为0°～15°下的海面同极化电磁散射系数的不同影响因素．

3.1　不同海域温度、盐度对海面散射的影响

图4给出擦地角2°,风速10 m/s下不同海域后向散射系数随擦地角的变化,表2中算例1~4温度盐度的取值跨度较大,代指不同海域特征．从图4可以看出,温度、盐度变化对不同频率海面电磁散射系数影响很小,仅为0.1 dB．

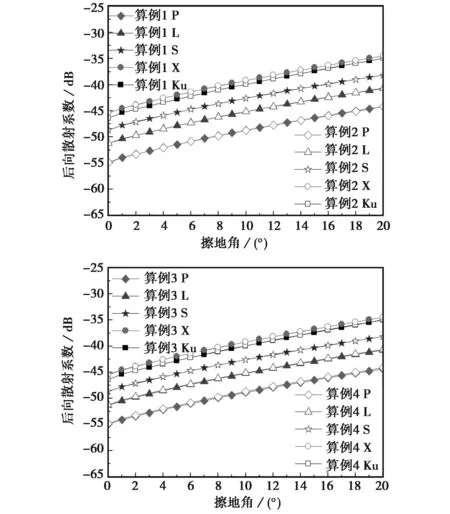
图4　不同海域后向散射系数随擦地角变化曲线

对给定频率的海面散射系数的影响主要来自于不同海域的海情与海况,注意到Ku频段散射系数小于X波段,其与雷达手册图15.5相一致[14],文章后节给出此时小擦地角下高频率存在临界角,散射系数下降很快．

表2　图4中不同算例取值

3.2　截断波数对海面散射的影响

为研究截断波数对海面散射的影响,我们保持其他条件不变仅改变截断波数,来计算海面后向散射系数,结果如图5所示．可以看出:随截断波数增大,仅对擦地角大于50°时的同极化后向散射系数有较大影响,而对于我们关注的小擦地角范围几乎没有影响,因此截断波数对于小擦地角海面同极化后向散射的影响是可以忽略的．

图5　不同kcut下同极化后向散射随擦地角变化曲线

3.3　相位对海面散射的影响

修正双尺度考虑了风向造成的浪涌倾斜,后向散射系数随方位角变化存在不对称性,如P波段．图6中擦地角为2°,风速变化范围5~10 m/s,可以看出:P/L波段,风向造成浪涌倾斜．随风速增大,散射系数增大,顺风与逆风的不对称逐渐消失,但风向影响仍明显;X和Ku波段,顺风与逆风散射系数不对称消失,风速与风向对VV极化散射系数影响明显,对HH极化的影响明显减弱,尤其风速较大时;由于泡沫体散射,HH极化与VV极化的散射系数幅度差减小．

3.4　波高对海面后向散射的影响

不同海域不同海情下,海面风速引起的波高也极为不同,对这一海域特征量,利用Andreas等人的研究[12]可以将其与风速联系起来,即

(13)

通过中国海洋大学提供的2013年8月不同海域的有效波高分布,选取不同海域如渤海有效波高约0.8 m,黄海有效波高1.0 m,东海有效波高1.5 m,南海有效波高2.0 m．

图6　多波段海面后向散射系数随相位角变化

由图7可以看出小擦地角下海面散射系数随波高增加而增加,同一海域波段频率增加,P/L/S/X波段散射系数依次增加,幅度约为2～3 dB,而Ku波段散射系数较X波段减小约1 dB,且随风速波高增加而差距减小,可见同一海域的散射系数不是频率的线性关系,频率相关性弱,同时因为所取角度接近海杂波临界角,此时泡沫反射对海面反射也产生干涉,可以看出模拟结果与雷达手册实验数据[14]类同,因此不同海域,给定频率散射系数的差异,主要决定于海态参数的不同．

图7　不同波高对多波段海面散射的影响

3.5　泡沫覆盖对小擦地角海面散射的影响

采用本文算法计算0～15°擦地角下的海面后向散射系数,结果如图8所示,点状数据为修正双尺度法计算结果,线性数据为含泡沫模型计算结果,其中虚线表示VV极化,实线表示HH极化．依据公式 (8),当风速在中低海情(风速小于10 m/s),覆盖率在0.66%以下,泡沫影响微小,故只计算风速分别为10 m/s(中高海情)、15 m/s(高海情),即覆盖率分别为0.665%、3.883%时多波段两种同极化的海面后向散射系数．

由图8可以得到:P、L波段泡沫对电磁散射系数影响可忽略,随风速增大,散射系数增大,主要是粗糙海面面散射的贡献,VV极化高HH极化10 dB左右;S波段泡沫对HH极化后向散射系数影响较大,随风速增加,达到4 dB左右,尤其小擦地角时;X与Ku波段,泡沫对后向散射系数影响达到10 dB左右,但随着擦地角增加这种影响减弱,尤其HH极化随着风速增加,增大较明显,同时可以看出,考虑泡沫影响后出现了海杂波观测中的临界角(1°左右)现象[14],同时随风速增大,泡沫覆盖率、层厚增加,面和体散射综合效应使后向散射随风速明显增大．海面后向散射高频与低频波段间的巨大差异也符合文献[3]的描述．

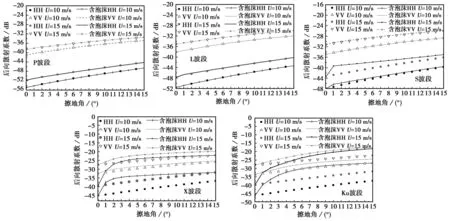
图8　不同海情有无泡沫影响下多波段海面后向散射系数随擦地角变化

4结论

国内外已经开展了大量海面电磁散射海杂波等实验．我们通过理论计算海面电磁散射,一方面验证了实验数据的电磁机理,比如海杂波中高频散射系数降低的情况,另一方面也为建立更为完善的理论模型提供参考,从中可以提炼更多的规律与思考,从而节约实验成本,扩展实际应用面．

本文建立在吴振森教授科研组[7,13]所完善的四修正双尺度法上,考虑海面泡沫[6,8]修正介电常数并引入海情海况相关的截断波数,研究小擦地角(0～15°)海面电磁散射．当波段大于S(3 GHz)时,泡沫才开始产生影响,理论计算得到HH极化10～15 dB的增强,而VV极化同比增加1～2 dB,同时只有在考虑了泡沫影响时才能看到海杂波实验中出现的临界角(大约1°擦地角)现象,这一现象导致了高频Ku波段电磁散射较X波段略小．

本文详细地分析了风速风向、波高、泡沫覆盖率、频率与极化等在小擦地角散射下对海面后向散射的影响,并以此阐述小擦地角电磁散射机理,研究中也有考虑不足的地方,一方面没有相应实验的支持,此外理论模型建立的较为简单,不够系统,进一步希望考虑实际海面破碎浪、浪涌,以及目标船舰等的影响,以此研究更为实际的海面电磁散射问题．

致谢本文工作是由国家自然科学基金支持,并在相关项目报告的基础上完成的,在此特别感谢导师吴振森教授的指导与意见．

[1] DALEY J, RANSONE Jr J, BURKETT J. Radar Sea Return-JOSS I[R]. Report of Nrl Progress, Washington, D.C: Naval Research Laboratory,1971, 2: 39-49.

[2] HELMKEN H F. Low-grazing-angle radar backscatter from the ocean surface[J]. IEE Proceedings F Radar and Signal Processing, 1990, 137(2): 113-117.

[3] NGO H D, RINO C L. Application of beam simulation to scattering at low grazing angles 1. Methodology and validation[J]. Radio Science, 1994, 29(6): 1365-1379.

[4] HWANG P A. SLETTER M A, TOPORKOV J V. Breaking wave contribution to low grazing angle radar backscatter from the ocean surface[J]. Journal of Geophysical Research: Part C:Oceans, 2008, 113:C09017. doi: 10.1029/2008JC004752.

[5] SAJJAD N, KHENCHAF A, COATANHAY A. Electromagnetic wave scattering from ocean surface at low grazing angle[C]//IEEE International Geoscience and Remote Sensing Symposium. Cape Town, 2009: IEEE, 196-199.

[6] JIN Yaqiu,HUANG Xingzhong, YIN Jieyi. The backscattering from rough sea surface with foam whitecap[J]. Acta Oceanologica Sinica, 1994, 16(4): 63-72. (in Chinese)

[7] WU Zhensen, ZHANG Jinpeng, GUO Lixin. An improved two-scale model with volume scattering for the dynamic ocean surface[J]. Progress in Electromagnetics Resarch, 2009, 89: 39-56.

[8] LUO Gen, ZHANG Min, YUAN Xiaofeng. Investigation of EM scattering from electrically large sea surface with breaking wave at low grazing angles[J]. Waves in Random and Complex Media, 2013,23(3): 226-242.

[9] MEISSNER T, WENTZ F J. The complex dielectric constant of pure and sea water from microwave satellite observations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(9): 1836-1849.

[10]SIHVOLA A H, KONG J A. Effective permittivity of dielectric mixtures[J]. IEEE Transactions on Geoscience and Remote Sensing, 1988, 26(4): 420-429.

[11]KUANG Kui,CHANG Man. The model and application of sea electromagnetic scattering[J]. Acta Oceanologica Sinica, 1992, 14(5): 34-44. (in Chinese)

[12]ANDREAS E L, EDSON J B, MONAHAN E C, et al. The spray contribution to net evaporation from the sea: A review of recent progress[J]. Boundray-Layer Meteorology, 1995, 72(1/2): 3-52.

[13]ZHANG Yandong, WU Zhensen. Modified two-scale model for low-grazing-angle scattering from two dimensional sea surface[J]. Chinese physics letters, 2002, 19(5): 666-669.

[14]SKOLNIK M. Radar Handbook [M]. Third Edition, America: McGraw-Hill Professional, 2008: 587-595.

吴涛(1990-),男,湖北人,西安电子科技大学在读博士研究生,主要研究方向为地、海面电磁散射及高性能计算方法.

吴振森(1946-),男,湖北人,西安电子科技大学教授,博士生导师,近年来主要从事复杂介质、非均匀介质中的电磁波/光波的传播与散射、目标激光散射特性和电磁散射等方面的研究.

Elements affecting low-grazing-angle electromagnetic scattering

properties from ocean surface at multi-band in different sea area

WU Tao1LINGHU Longxiang1WU Zhensen1SU Xiang1SUN Tianqi2

(1.SchoolofPhysicsOptoelectronicEngineering,XidianUniversity,Xi’an710071,China;

2.OceanUniversityofChina,Qingdao, 266071,China)

AbstractBased on satellite data of sea surface temperature and salinity at Southeast coast and the Western Pacific, dual-Debye model and M-G mixed media theory with foam are applied to calculating sea effective permittivity, analysis shows that different area changes in temperature and salinity will have great impact on imaginary part of permittivity at P/L-band and have little impact on other bands, where the affecting of permittivity on a given frequency sea scattering coefficient has the range of only 0.1dB, thus the sea condition and state are of significant importance. Based on the modified two-scale model and VRT, considering the cut-off wavenumber at different frequency and sea states, numerical results show the low grazing angle electromagnetic backscattering at multi-band (P/L/S/X/Ku-band) in different sea area, and the affection of windspeeds and directions, foam cover, frequencies and polarization are considered at the same time. The mechanism of multi-scale low grazing angle electromagnetic scattering is also analyzed.

Key wordslow-grazing-angle; multi-band; modified two-scale model; ocean electromagnetic backscattering

作者简介

收稿日期：2014-12-09

中图分类号TN011

文献标志码A

文章编号1005-0388(2015)06-1078-08