基于时变步长最小均方算法的射频干扰对消

刘建成　全厚德　赵宏志　孙慧贤　潘成康

(1.解放军军械工程学院,石家庄 050003;2.电子科技大学 通信抗干扰技术国家级重点实验室,

成都 611731;3.中国移动通信有限公司研究院,北京 100053)



基于时变步长最小均方算法的射频干扰对消

刘建成1全厚德1赵宏志2孙慧贤1潘成康3

(1.解放军军械工程学院,石家庄 050003;2.电子科技大学 通信抗干扰技术国家级重点实验室,

成都 611731;3.中国移动通信有限公司研究院,北京 100053)

摘要针对同时同频全双工系统中射频域干扰对消收敛速度与对消比相互制约的问题,提出基于时变步长最小均方算法的射频自干扰对消方法.该方法在正交两路合成干扰对消方案基础上,利用Logistic函数非线性关系实时改变步长因子,在最小均方准则下实现两路衰减器的快速精确调整,完成自干扰信号的有效对消.最后，理论分析了该对消方法的收敛性和稳态失调误差，给出了收敛状态下能够获得对消比的闭合表达式.理论分析和仿真表明，该方法的收敛时间缩短为已有变步长对消方法的1/4,最终达到的对消比与已有方法相比提高了约5 dB.

关键词射频干扰对消;最小均方算法;收敛速度;对消比

资助项目: 国家自然科学基金(U1035002/L05, 61001087, 61101034, 61271164); 国家科技重大专项(2014ZX03003001-002, 2012ZX03003010-003, 2011ZX03001-006-01); 中国移动通信有限公司研究院合作项目

联系人： 刘建成 E-mail：liujiancheng1987@126.com

引言

21世纪是信息时代,人们对信息传输速度的要求日益增强,这就需要更宽的通信频率带宽.目前无线频谱资源日益紧张,如何有效提高频谱利用效率成为了当前急需解决的问题.传统的频分双工(Frequency Division Duplexing, FDD)通信体制所需频谱资源多[1],时分双工(Time Division Duplexing, TDD)的信息传输速率低[1],这些技术已不能有效满足人们目前的需求.同时同频全双工(Co-frequency and Co-time Full Duplex, CCFD)技术在同等带宽下,理论上具有两倍于传统双工的传输速率[1],能够克服传统双工频谱资源浪费和传输速率低的不足,受到广泛关注,成为目前众多研究机构和学者们研究的对象.不过,该通信技术的实现必须建立在其自干扰有效消除的基础上.

CCFD技术的核心是自干扰消除,在一般应用中需具有110 dB的自干扰抑制能力[2],目前主要通过两种途径解决,被动干扰抑制和主动干扰对消.被动干扰抑制是指通过对收发天线位置和方向性等方面的设计,增加收发通道间的隔离度,降低自干扰信号与期望信号功率之比,抑制比约为25~40 dB[3-5].主动干扰对消主要包括射频(模拟)域和数字域两类[2],二者共同作用才可实现自干扰的有效对消.数字域干扰对消利用发送信号的导引序列估计自干扰信道[2,6],进而由已知的发送信号重建干扰,再与接收信号对消.该方法的对消比(Interference Cancellation Ratio, ICR)约为30 dB[2].

射频域自干扰对消能够保证接收通道不被阻塞,同时降低对模数转换器(Analog Digital Convert,ADC)器件量化位数和动态范围的要求[7],是后续数字域干扰对消的基础,在CCFD技术中具有举足轻重的地位.文献[1,8]采用数模转换器(Digital Analog Convert,DAC)之前引出参考信号,通过与发送信号相对应的射频通道,最终对消接收的自干扰信号.该方法便于延时与幅度衰减的调节,但由于参考信号与自干扰信号通过了不同射频通道,故不能够有效抑制自干扰信号非线性成分, ICR只能达到30~35 dB[9].文献[5,10]提出了在射频放大器与发送天线之间引出参考信号的对消方案,在噪声消除芯片(型号: QHx220)上实现了基于最速下降法的正交两路幅度增益的反馈控制,通过幅度调节合成信号的相位,完成最终的自干扰信号对消.文献[11]在文献[5,10]对消方案基础上,提出了基于最速下降法的射频域自适应干扰对消方法,该方法以最速下降法代价函数为目标函数,解决了射频域维纳滤波难以实现的问题,从而实现了自适应干扰对消.文献[12]详细分析了射频域自适应干扰对消方法的收敛速度和稳态性能,并通过不同参数的实验验证了其性能.文献[13]分析了射频对消中器件精度等因素引起的幅度和相位误差对最终对消性能的影响.不过,文献[5,10-11]的射频域自适应干扰对消方法均采用固定的步长因子,这使得对消比将随步长因子变小而提高,收敛速度会随步长因子变小而减慢,即对消比与收敛速度二者相互制约.

由以上的分析可知,已有CCFD射频域自干扰对消方法多采用发送天线前端引出参考信号的自适应干扰对消方案,不过其自适应控制方法的收敛速度和对消比不能兼得.因此,提出了基于时变步长最小均方算法的射频域干扰对消方法.该方法首先建立最小均方算法步长因子随时间变化的改进Logistic函数非线性关系,在保证高的对消比情况下有效提高收敛速度.与已有变步长干扰对消方法相比,该方法既可获得约5 dB的ICR增益,又可将收敛速度提高4倍以上.

1CCFD射频域自干扰对消原理

1.1　CCFD的系统模型

CCFD通信技术是利用同一频率同时收发信息,传输速率在理论上可以两倍于传统全双工,其基本结构如图1所示[2].图中的射频和数字域干扰对消是实现CCFD必不可少的环节,射频域干扰对消关键在于,如何利用输入至发射天线的射频信号sRF(t)无失真地构建出接收信号r(t)中的自干扰成分sI(t),进而反相合并.

结合图1知,可将发射天线耦合器至接收天线耦合器的传播空间及二者连接线等效为发送信号sRF(t)通过的信道h(t),考虑实际系统的因果性,有

(1)

式中,*表示卷积运算.则接收信号r(t)可表示为

r(t)=sI(t)+d(t)+ε(t)

(2)

ε(t)表示系统中的加性高斯白噪声.

CCFD系统射频域干扰对消的关键即在于如何在射频域有效估计自干扰信道响应h(t),在非移动的简单应用场景中,该信道可视为线性的,对自干扰信号的影响主要是幅度衰减和时延.

1.2　CCFD系统的射频对消基本原理

针对图1所示的CCFD系统结构和式(2)的接收信号模型,文献[14]根据实际线缆长度和天线间距预先估计出自干扰信道的时延,该时延参数的精度受限于现有延时器件,故不再对其进行分析.在设定时延的基础上,通常采用正交合成的方法估计干扰信号sI(t)的幅度衰减和相位变化.该方法如图2所示,将发送通道的射频信号sRF(t)延时τ′后分成si(t)和sq(t)两路,si(t)与原信号相同,sq(t)为si(t)通过90°移相器的正交分量,其中延时器是估计干扰信号的群延迟.

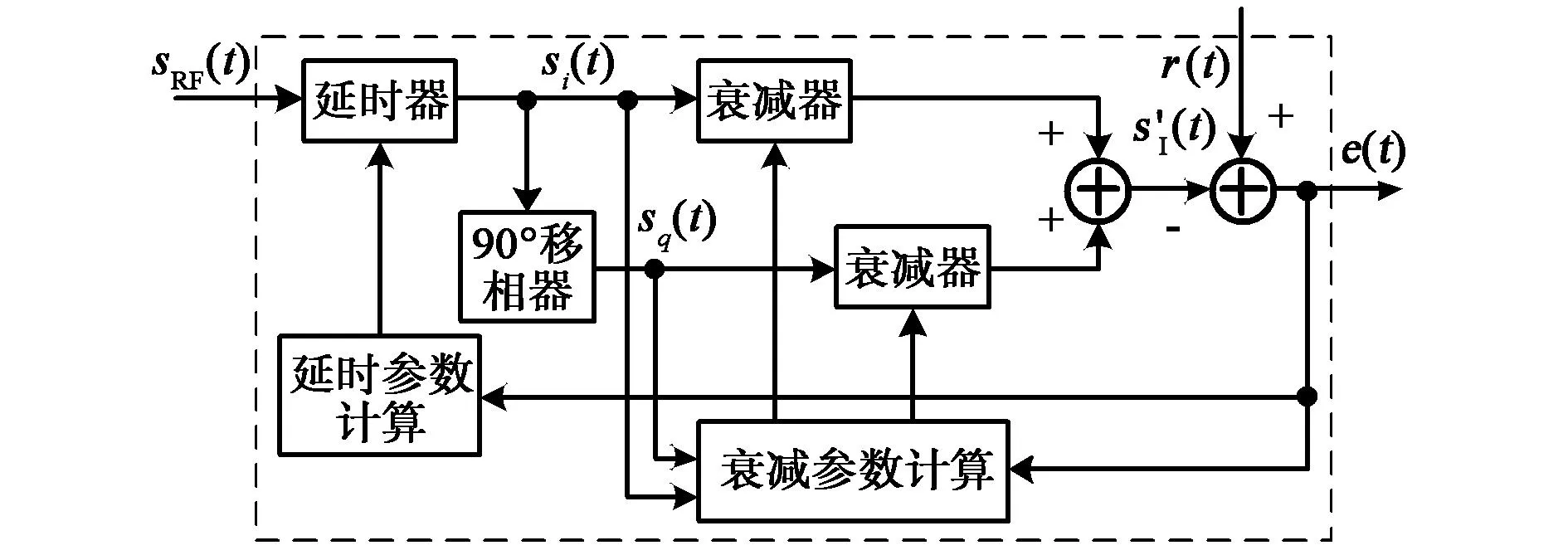
图2　射频自干扰对消原理图

图3　衰减参数反馈计算实现结构

由上述内容可知,若令s(t)=[si(t)sq(t)]T,则已有射频干扰对消的基本过程可表示如下:

(3)

(4)

(5)

可见,上述的干扰对消过程即最小均方(Least Mean Square, LMS)算法的实现,是基于最小均方误差准则,即

min{E(|e(t)|2)}=min{E(|r(t)-

(6)

式中,|·|2表示模值的平方.

综上所述,在信道时延估计确定情况下,衰减器参数的反馈控制是影响射频域干扰对消性能的关键因素,已有射频干扰对消方法的收敛速度与参数调整精度相互制约,影响了最终的对消性能.

2基于时变步长LMS射频干扰对消

LMS算法收敛时间随步长因子μ的增大(满足收敛条件)而减少,但稳态失调误差会随μ的增大而增大.因此,文献[17-18]提出了变步长方法,使得步长因子μ在算法初始阶段具有较大值以提高收敛速度,在接近收敛时值变小以降低稳态失调误差.不过,已有变步长方法容易受外界相关噪声等因素影响,且多是针对数字域的处理,计算复杂,无法在模拟域实现.为弥补不足,提出新的时变步长LMS算法(Time-Varying Step-Size LMS, TVSSLMS),步长因子随时间的推移由大逐渐减小,不受误差信号大小的约束,从而有效提高对消比.

2.1　基于TVSSLMS的射频干扰对消模型

文献[15]中对LMS算法性能进行了详细的理论分析,表明该算法是维纳滤波解的递推求解过程,可利用模拟电路器件实现.同时给出了步长因子取值需满足的条件为

i=0,…,M′-1}.

(7)

式中:M′为算法滤波阶数;λi为参考信号统计自相关矩阵(M′×M′维)特征值. 对于图3和式(3)~(5)所示的模拟域LMS算法,由于参考信号分为功率相等的正交两路si(t)和sq(t),设功率均为Ps,则由二者构成的参考信号向量s(t)的统计自相关矩阵为

(8)

可见,图2所示LMS算法中参考信号自相关矩阵的特征值相等,即为正交两路信号功率Ps.

为使步长因子取值满足式(7)所示的收敛条件,且在收敛时具有小的稳态失调误差,需对步长因子取值加以限定.考虑Logistic函数符合初值大,之后逐渐变小的特点,但其变化趋势缓慢,制约了进一步提高收敛速度和减小稳态失调误差,故对其加以改进,缩短函数取值由大到小的变化过程.以此建立步长因子与时间t的非线性关系,形成TVSSLMS算法核心为

(9)

式中:μmin是设定的步长因子最小值;μmax是由式(7)设定的步长因子最大值;κ是需根据不同情况设定的调整参数,控制了μ(t)随t变换的快慢;t0是步长因子改变对应的起始时刻,初始值为0.由表达式可知μ(t)随t单调递减,且其导数为钟形,钟形的宽度可由参数κ调控.

在上述变步长基础上,基于TVSSLMS射频干扰对消中两路衰减器的参数调整由式(5)变为

(10)

为了使TVSSLMS算法具有应对自干扰信道h(t)突变的能力,伴随步长因子的变化,通过检测对消后误差信号瞬时功率的变化,判断干扰信号幅度和相位是否发生突变.在此基础上,基于TVSSLMS算法的射频干扰对消模型如图4所示,基本流程如下:

图4　时变步长LMS干扰对消模型

1) 算法初始,由文献[14]中的方法估计传输线缆及收发天线的总延时τ′,根据已知参考信号si(t)和sq(t)的功率值设定步长因子的最大值μmax、最小值μmin和κ,步长因子变化起始时刻t0=0;

2) 将1)中参数代入式(9),以时间TΔ为间隔计算步长因子μ(t),之后执行式(3),(4)的LMS算法;

3) 估计收敛状态下误差信号e(t)的瞬时功率,与前一时刻误差信号e(t-TΔ)比较,若大于设定的门限值χ,则执行步骤4),小于则直接返回执行步骤2);

4) 将当前算法执行时间t赋值给步长变化起始时刻t0,返回执行步骤2).

其中误差信号瞬时功率计算为

(11)

2.2　性能分析

在第1.2和2.1节叙述TVSSLMS射频干扰对消方法原理和流程基础上,本节将从理论上分析该对消方法性能,推导出算法步长因子与收敛性之间的关系,给出该方法的最终ICR表达式.

s(t)+d(t)+ε(t),

(12)

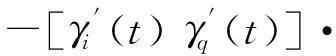
s(t))2}.

(13)

e(t)=cT(t)s(t)+d(t)+ε(t).

(14)

将式(14)代入式(13)得

E{|e(t)|2}=E{cT(t)s(t)sT(t)c(t)+

2cT(t)s(t)[d(t)+ε(t)]+

[d(t)+ε(t)]2}.

(15)

由于ε(t)和d(t)统计独立,且与参考信号向量s(t)不相关,利用直接平均法[15]可得

E{|e(t)|2}=E{cT(t)·R(0)·c(t)}+

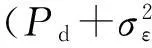
(16)

式中,R(0)如式(8)所示,是参考信号向量s(t)的统计平均自相关矩阵,为2×2的对角阵.由式(10)可得

c(t+TΔ)=c(t)-μ(t)s(t)e(t)

=[I-μ(t)R(0)]c(t)-

μ(t)s(t)[d(t)+ε(t)].

(17)

因输入参考信号向量s(t)与期望信号d(t)、白噪声ε(t)不相关,故式(16)可根据式(17)化简为

=E{cT(t-TΔ)R(0)·[I-μ(t-

TΔ)R(0)]2c(t-TΔ)}+2μ2(t-

(18)

若假设t=nTΔ,以此类推,有

E{|e(t)|2}=E{cT(0)ψ(t)c(0)}+

(19)

式中:

ψ(kTΔ)=

(20)

φ(kTΔ)=

(21)

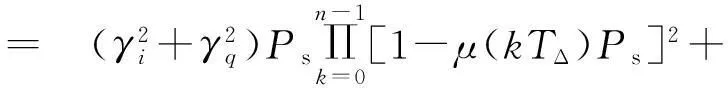
(22)

可见式(22)收敛条件为:对于任意的k均有|1-μ(kTΔ)Ps|<1,与式(7)给出的LMS算法收敛条件相符.根据式(22)与定步长LMS算法(Fixed Step-Size LMS, FXSSLMS)对比分析所提方法性能.

由上述分析可知,算法收敛性由式(22)中累积乘积取值的变化趋势决定,对于FXSSLMS算法μ(t)为常数,即TVSSLMS和FXSSLMS算法收敛因子[15-16]分别为ρTVSS(nTΔ)和ρFXSS(nTΔ):

(23)

ρFXSS(nTΔ)=(1-μPs)2n.

(24)

设Ps=1,FXSSLMS算法步长因子为μ=0.1/Ps, TVSSLMS的μmax=8μ、μmin=0.5μ,则两种算法的理论收敛曲线如图5所示.对于一般情况,当ρ(nTΔ)<10-30时可近似为0,由图可见TVSSLMS算法收敛速度明显快于FXSSLMS算法.

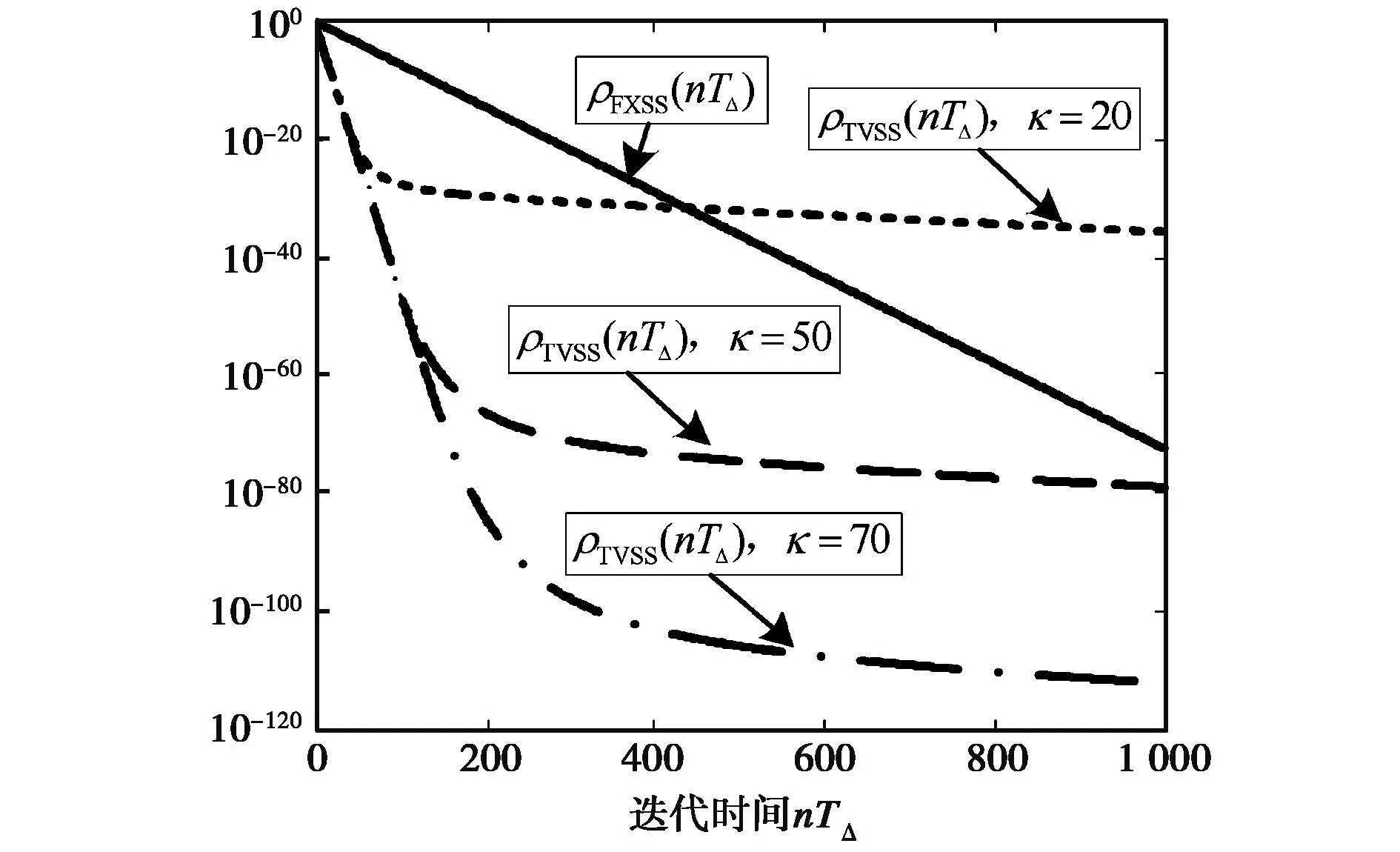
图5　不同参数对应的收敛因子变化曲线

为便于分析,由式(9)知t≥NTΔ有μ(nTΔ)≈μmin,则t≥NTΔ的均方误差可由式(22)等价为

(25)

因|1-μminPs|<1,当t→∞有(1-μminPs)2(n-N)逼近0.所以,t→∞对应的误差信号均方值为

(26)

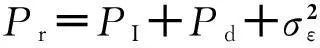
(27)

在以上算法性能分析基础上,可设定步长因子最大值μmax=0.8/Ps,同时参考式(27)设定步长因子最小值.另外,式(9)中参数κ取值需依据实际情况而定,过大和过小均易导致不能在最短时间内收敛到最高ICR,从而降低算法的性能.当ρTVSS(nTΔ)小于10-30可认为算法处于收敛状态,结合步长因子导数变化趋势知,若兼顾收敛速度和ICR,则算法收敛时刻,即ρTVSS(nTΔ)≤10-30时步长因子应处在变化最快的区域,即处于钟形中心位置.所以,迭代变

步长式(9)中的参数κ需满足以下两个关系式:

(28)

ρTVSS(nTΔ)≤10-30.

(29)

3实验结果分析

本节将对基于TVSSLMS算法的射频干扰对消仿真,与已有变步长LMS算法进行对比,并仿真分析时延估计误差和衰减器响应时间对TVSSLMS对消方法的影响.仿真以传输速率为20Mbps,载频为2.1GHz的QPSK调制为例.射频前端非线性三阶交调抑制比为35dB,发射功率30dBm,即1W,天线隔离度为40dB,接收的期望信号功率为-75dBm,参考文献[2]设接收通道噪声限为-95dBm.由于实际的CCFD场景中收发天线相距较近,自干扰信号主径远大于反射路径,故这里暂不考虑反射多径的影响.本节所有结果均是200次独立仿真所得.

3.1　与已有变步长LMS方法对比分析

在上述条件下,考虑射频域实现的约束,本小节仿真对比TVSSLMS算法与文献[17-18]变步长LMS算法的收敛性与最终所能达到的ICR,暂假设图2中的延时估计误差为0,图4中的TΔ=100 ns.由收发天线间隔离度和发送信号功率可初步估计出自干扰信号强度,从而设定参考信号的功率,本文仿真设参考信号功率值为0 dBm.由公式(7)、(8)和参考信号功率,令TVSSLMS算法和文献[17-18]算法中μmax=0.5,常规FXSSLMS算法步长因子取0.1μmax.参考文献[17-18]中参数设置原则,三种算法具体参数如表1所示,分两种情况进行仿真对比,FXSSLMS参数不变.

表1　不同方法对应参数

另外,为检验上述方法应对自干扰信号相位突变的能力,设定t=15μs时自干扰信号相位发生改变.参数 1、2对应的ICR收敛曲线结果分别如图6、7和表2所示.由图6和表2可见,参数1对应的FXSSLMS、文献[17]和[18]算法最终ICR相近,分别为76.75dB,76.22dB和76.15dB,而TVSSLMS算法最终能够达到的ICR为86.32dB,提高了约10dB.对比参数1中四种方法,首次收敛时ICR达到60dB所需的收敛时间,FXSSLMS收敛速度最慢,需4.92μs,其次是文献[17]需3.55μs,文献[18]需2.90μs,而TVSSLMS方法仅需0.85μs,收敛速度比已有对消方法提高3倍以上.当自干扰信号相位突变,TVSSLMS方法能够迅速再次达到收敛状态,速度明显快于其他三种方法,具有很好的自适应跟踪能力.另外,将参考信号功率、自干扰信号功率、期望信号和噪声功率,以及参数1本文方法的最小步长因子0.005代入式(27),计算最终ICR理论值为87.96dB,与仿真结果相符,从而验证了ICR理论闭合表达式(27)的正确性.

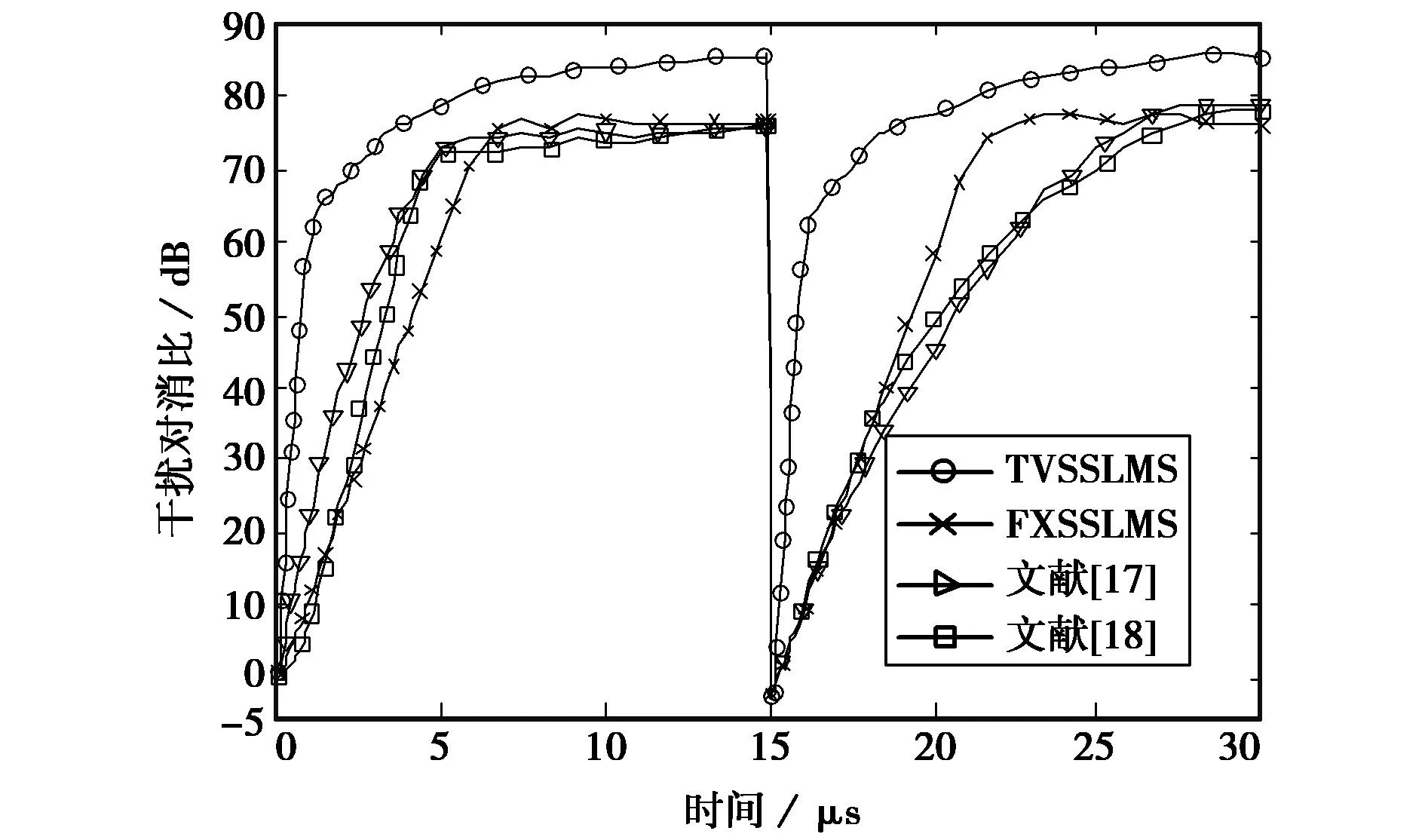
图6　参数1对应的四种方法ICR曲线

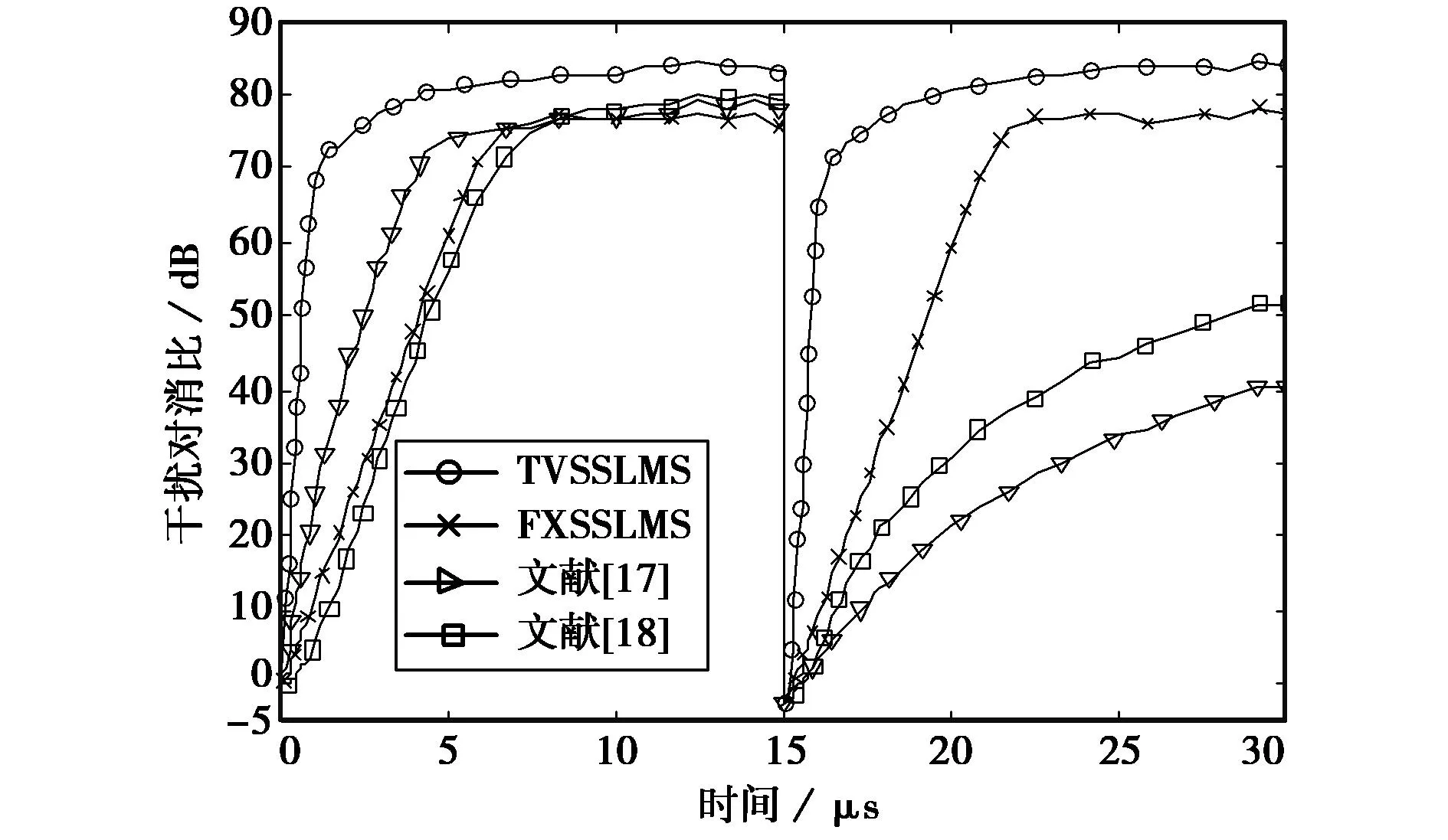
图7　参数2对应的四种方法ICR曲线

对于参数2,TVSSLMS方法最终的ICR比FXSSLMS对消方法提高了7dB以上,比文献[17]高出了约3.7dB,比文献[18]提高了近5dB.对于ICR达到60dB所需的收敛时间,文献[17]和[18]两种方法相对于参数1分别增加为5.40μs和3.65μs,TVSSLMS方法和定步长LMS法与参数1结果基本相等,故在此参数下收敛速度比已有方法提高了4倍以上.对比相位突变后的ICR曲线,表明该参数下TVSSLMS方法与另外三种相比具有更强的自适应跟踪能力.

另外,对比两种参数中本文算法的步长因子最小值,图6、7中收敛曲线变化趋势以及表2的最终ICR,可发现最终ICR将相差约2.2dB,同样验证了式(27)的正确性,同时步长因子最小值也影响收敛速度,与式(22)和(24)相对应.

由以上可知,文献[17]和[18]两种变步长LMS对消方法,在两种仿真参数下均低于TVSSLMS对消方法.这是因为两种方法的步长因子均受反馈误差信号控制,而本文的对消模型中反馈误差包含噪声和期望信号,且期望信号本身前后具有相关性,致使两种方法的步长因子不能足够小,最终达到的ICR偏低.而TVSSLMS对消方法克服了该不足,步长因子不受反馈误差信号本身相关性的影响,既能够达到高的ICR,又具有快的收敛速度.

表2　两种参数仿真结果对比

3.2　不同时延误差和时间步进的仿真对比

在3.1节仿真条件基础上,将仿真分析图2中时延估计误差τΔ和图3中时间步进TΔ对本文方法的影响.为更加贴近实际器件的性能[19],仿真设时间估计误差τΔ分别为0.062 5ns,0.25ns和0.5ns三种情况(步进TΔ=100ns),步进TΔ为50ns,150ns,300ns三种情况(时延误差为0),其仿真结果分别如图8和9所示.

由图8知,在步进间隔TΔ=100ns,三种时延估计误差τΔ最终的ICR分别为58.699 7dB,46.640 1dB和40.632 6dB.由表2可知τΔ=0时本文方法ICR为86.82dB,可见ICR随时延估计误差的增大下降明显,不过当估计误差达到0.062 5ns时仍能获得58dB以上的ICR,具有较高的实用性.

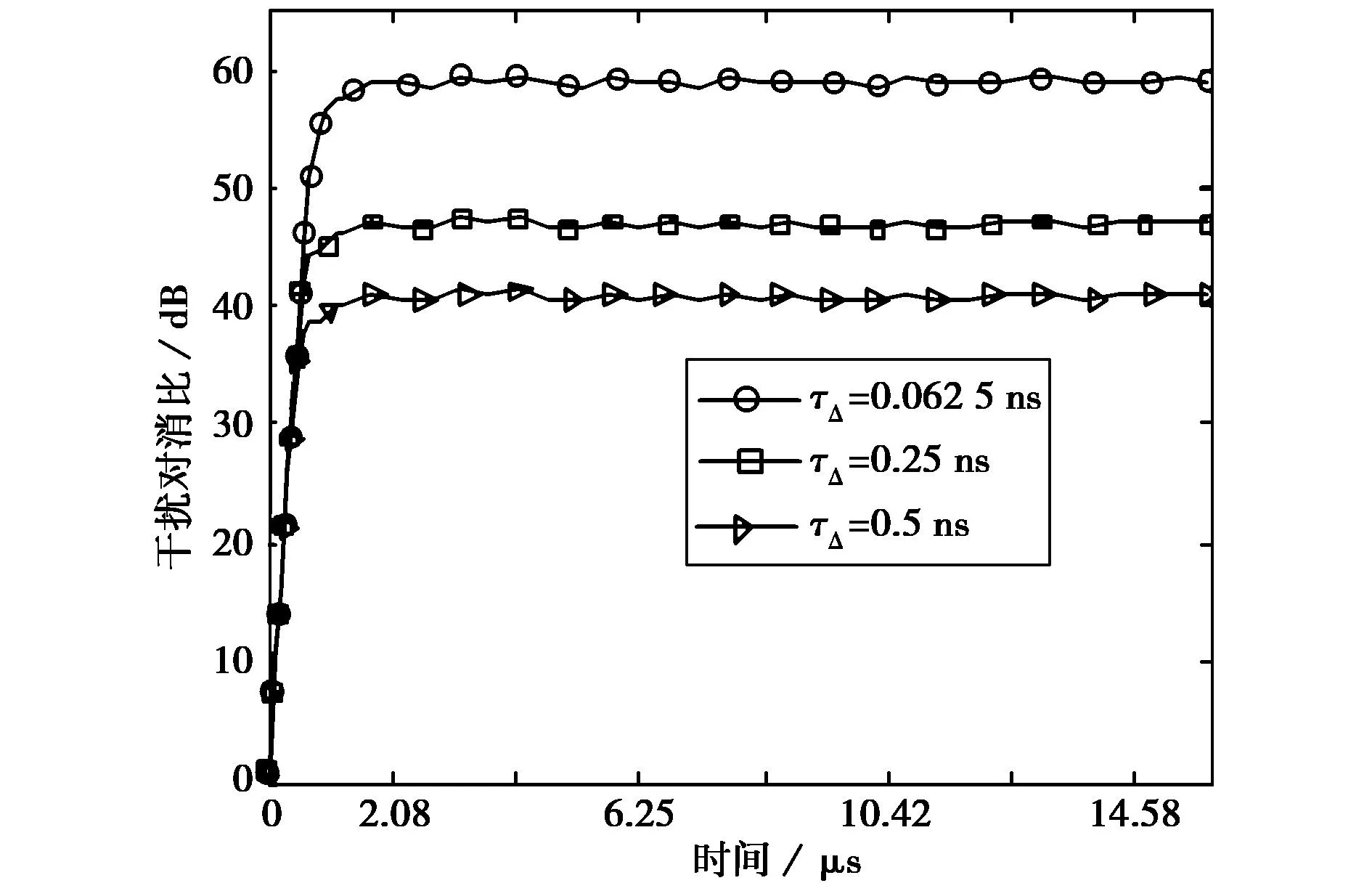
图8　不同时延误差对本文对消方法影响

图9　不同时间步进对本文对消方法影响

由图9可见,当TVSSLMS对消方法最小步长固定不变,不同步进间隔TΔ仅影响了其收敛时间,并未改变最终ICR.随着步进间隔的增大,TVSSLMS对消方法的收敛时间将增加,当时间步进TΔ=300ns时,ICR达到60dB所需收敛时间为1.69μs.可见,基于TVSSLMS对消方法在反馈控制环路时间步进为300ns,仍具有快的收敛速度,可满足工程实现要求.

4结论

针对CCFD射频域干扰消除问题,论文给出了基于时变步长LMS算法的干扰对消方法,通过时间因子控制算法的步长大小,既有效提高了对消方法的收敛速度,又能够保证获得高的干扰对消比.与已有变步长LMS对消方法相比,所提方法的最终ICR提高了约5dB,ICR达到60dB时所需的收敛时间缩短为已有方法的1/4.在贴近现有器件精度下,基于时变步长LMS的射频域干扰对消方法最终ICR仍能够达到近60dB.所以,论文提出的射频域干扰对消方法具有快的收敛速度和高的对消比,且便于射频域实现,具有较高的实际应用价值.不过,该方法暂时未考虑自干扰构建引入新的非线性信号消除问题,下一步仍需进行更为深入的研究.

参考文献

[1]DUARTEM,CHRISD,ASHUTOSHS.Experiment-drivencharacterizationoffull-duplexwirelessSystems[J].IEEETransactionsonCommunicationsonWirelessCommunications, 2012, 11(12): 4296-4307.

[2]DINESHB,EMILYM,SACHIN.FullDuplexRadios[C]//ProceedingsoftheACMSIGCOMM2013conferenceonSIGCOMM.ACM, 2013: 375-386.

[3]KNOXME.Singleantennafull-duplexcommunicationsusingacommoncarrier[C]//WirelessandMicrowaveTechnologyConference(WAMICON), 2012IEEE13thAnnual, 2012.

[4]BOZIDARR,DINANG,KEYP,etal.Rethinkingindoorwirelessmeshdesign:lowpower,lowfrequency,full-duplex[C]//WirelessMeshNetworks, 2010FifthIEEEWorkshopon, 2010: 1-6.

[5]CHOIJI,JAINM,KANNANS,etal.Achievingsinglechannel,full-duplexwirelesscommunication[C]//ProceedingsoftheSixteenthAnnualInternationalConferenceonMobileComputingandNetworking.ACM, 2010: 1-12.

[6]KORPID,ANTTILAL,SYRJALAV,etal.Widely-lineardigitalself-interferencecancellationindirect-conversionfull-duplextransceiver[J].IEEEJournalonSelectedAreasinCommunications, 2014, 32(9): 1674-1687.

[7]RIIHONENT,WICHMANR.Analoganddigitalself-interferencecancellationinfull-duplexMIMO-OFDMtransceiverswithlimitedresolutioninA/Dconversion[C]//2012ConferenceRecordoftheFortySixthAsilomarConferenceonSignals,SystemsandComputers(ASILOMAR).IEEE, 2012: 45-49.

[8]DUARTEM.Full-duplexWireless:Design,ImplementationandCharacterization[D].Houston:RiceUniversity, 2012.

[9]DEBAILLIEB,BROEKDJ,LAVINC,etal.Analog/RFsolutionsenablingcompactfull-duplexradios[J].IEEEJournalonSelectedAreasinCommunications, 2014, 32(9): 1662-1673.

[10]JAINM,CHOIJI,KIMT,etal.Practical,real-time,full-duplexwireless[C]//Proceedingsofthe17thAnnualInternationalConferenceonMobileComputingandNetworking.ACM, 2011: 301-312.

[11]CHOIYS,HOOMANSM.Simultaneoustransmissionandreception:algorithm,designandsystemlevelperformance[J].IEEETransactionsonCommunicationsonWirelessCommunications, 2013, 12(12): 5992-6010.

[12]LIWL,ZHAOZH,TANGJ,etal.Performanceanalysisandoptimaldesignoftheadaptiveinterferencecancellationsystem[J].IEEETransactionsonElectromagneticCompatibility, 2013, 55(6): 1068-1075.

[13]何昭君, 沈莹, 邵士海, 等. 自干扰幅度及相位误差对全双工系统的影响[J]. 电波科学学报. 2014, 29(5): 827-832.

HEZhaojun,SHENYing,SHAOShihai,etal.BERperformanceofco-timeandco-frequencyfull-duplexsystemwithphaseandamplitudecancellationerrors[J].ChineseJournalofRadioScience, 2014, 29(5): 827-832.(inChinese)

[14]徐强,全欣,潘文生,等. 同时同频全双工LTE射频自干扰抑制能力分析及实验验证[J]. 电子与信息学报, 2014, 36(3): 662-668.

XUQiang,QUANXin,PANWensheng,etal.AnalysisandexperimentalverificationofRFself-interferencecancelationforco-timeco-frequencyfull-duplexLTE[J].JournalofElectronics&InformationTechnology, 2014, 36(3): 662-668. (inChinese)

[15]HAYKINS. 郑宝玉,译.自适应滤波器原理[M].4版. 北京:电子工业出版社,2010: 206-212.

[16]ZHANGS,ZHANGJS.Newsteady-stateanalysisresultsofvariablestep-sizeLMSalgorithmwithdifferentnoisedistributions[J].IEEESignalProcessingLetters, 2014, 21(6): 653-657.

[17]TYSEERA,MAYYASK.Arobustvariablestep-sizeLMS-typealgorithm:analysisandsimulations[J].IEEETransactiononSignalProcessing, 1997, 45(3): 631-639.

[18]HUANGBY,XIAOYG,SUNJW,etal.Avariablestep-sizeFXLMSalgorithmfornarrowbandactivenoisecontrol[J].IEEETransactionsonAudio,SpeechandLanguageProcessing, 2013, 21(2): 301-312.

[19]HittiteMicrowave.BroadbandAnalogTimeDelaySMT,DC-24GHz[EB/OL][2015-01-09].http://www.hittite.com/products/view.html/view/HMC910LC4B. 2015.

刘建成 (1987-),男,河北人,在读博士研究生,研究方向为无线通信干扰抑制和通信信号自适应处理.

全厚德(1963-),男,辽宁人,博士,教授,博士生导师,研究方向为无线通信技术、指挥系统、通信设备性能测试.

赵宏志(1978-),男,河北人,博士,副教授,研究方向为无线信号处理及抗干扰技术.

孙慧贤 (1980-),男,内蒙古人,博士,讲师,研究方向为指挥控制系统抗干扰技术.

潘成康(1978-)，男，江苏人，博士，主要研究方向为第五代移动通信技术.

吴涛,令狐龙翔,吴振森,等．不同海域多波段小擦地角海面散射特性的影响因素分析[J]. 电波科学学报,2015,30(6):1078-1085. doi: 10.13443/j.cjors. 2014120901

WU Tao, LINGHU Longxiang, WU Zhensen, et al. Elements affecting low-grazing-angle electromagnetic scattering properties from ocean surface at multi-band in different sea area[J]. Chinese Journal of Radio Science,2015,30(6):1078-1085. (in Chinese). doi: 10.13443/j.cjors. 2014120901

RF interference cancellation based on time-varying

step-size least mean square algorithm

LIU Jiancheng1QUAN Houde1ZHAO Hongzhi2SUN Huixian1PAN Chengkang3

(1.OrdnanceEngineeringCollegeofPLA,Shijiazhuang050003,China; 2.NationalKey

LaboratoryofScienceandTechnologyonCommunications,UniversityofElectronicScience

andTechnologyofChina,Chengdu611731,China;3.ResearchInstitutionof

ChinaMobile,Beijing100053,China)

AbstractA new cancellation method based on time-varying step-size least mean square algorithm is proposed to compromise the convergence speed and cancellation ratio of radio frequency (RF) cancellation methods for co-frequency and co-time full duplex (CCFD) in this paper. This method is constructed on cancellation scheme with a composite of in-phase and quadrature signals, and the nonlinear characteristic of logistic function is utilized to vary step-size. Then the two attenuators are accurately fine-tuned by varying step-size and least mean square criterion to cancel the self-interference. Finally, we analyze the convergence and misadjustment steady-state error of this interference cancellation method in theory, and extract the closed expression of convergent cancellation ratio. Theory analysis and simulations verify that convergence time of proposedmethod is only a quarter of existing methods and lasted cancellation ratio is more 5 dB than existing methods.

Key wordsRF interference cancellation; least mean square algorithm; convergence speed; cancellation ratio

作者简介

收稿日期：2015-01-09

中图分类号TN911.72

文献标志码A

文章编号1005-0388(2015)06-1069-09