初中数学中“二次函数”的教学策略探微

◆江苏省扬州市广陵区北洲中学 朱彦雄

初中数学中“二次函数”的教学策略探微

◆江苏省扬州市广陵区北洲中学 朱彦雄

二次函数是初中数学教学的重要内容，在教学过程中，教师要转变教学观念，以学生为学习主体，在掌握基本概念的基础上分清不同数学知识的规律。文章提出，要采取数形结合的教学方法，让学生从生活中找实例进行探究，从而不断提高数学的学习能力。

初中数学；二次函数；教学策略

二次函数是初中数学的重点内容，在初中时期掌握好二次函数的知识，对今后学习和工作都有着极大的帮助。这一部分的数学知识需要较强的数学思维能力，学习难度较大，只有采用有效的教学方法，充分激发学生的学习兴趣，才能让学生从根本上掌握这部分知识。

一、改变教学观念，调动学生的积极性

教学观念是教师教学的先导，教学观念的正确与否决定了教师整体教学思路是否正确，能否让学生真正掌握知识。在传统数学教学中，学生只是知识的接受者，缺乏自己独立的思考。在新课改的要求下，教师要转变教学观念，将课堂主动权交给学生，改变原有的灌输式教学，以启发式的教学为主要方式，引导学生主动进行思考，不仅重视学生知识的接受程度，也关注学生学习能力是否提高。在教学的过程中，要尊重每个学生的学习个性，尊重差异，为每位学生打造适合他们学习的模式。对于二次函数这部分较难的知识，转变教学观念实施新式教学有利于学生认真对待学习，努力进行探究，也能培养学生养成良好的思考习惯。

除了教师的教学观念需要转变外，学生对学习的态度也是决定教学成败的重要因素。所以在设计二次函数的教学时，要能够抓住学生的兴趣点，使他们从学习中获得乐趣，才能将充足的热情投入到学习中来。数学本身是比较抽象的学科，为了使学生能够更加直观、具体地学习知识，教师在教学过程中就要合理运用多媒体技术，将图象和数字结合起来，让学生快速地理解相关内容。例如，在讲解y=ax2+bx+c的函数图象时，就可以利用多媒体技术，将不同的a，b，c的值进行比对，了解不同的系数对于函数式的影响。最主要的是将a，b，c等于0时的图象进行着重讲述，并让学生思考这些图象的特点是什么，有没有特殊的规律在里面。通过多媒体中十分形象的图象变换，学生就能很快理解这些不同系数下函数式的含义，并且能够牢固记忆，在以后解题的运用中能够轻车熟路。

二、明确基本概念，区分其他数学知识

数学概念是学习数学知识前必须要掌握的部分，但是在之后的应用中，很多学生会忘记基本概念，完全靠着自己的感觉做题，即使结果是正确的也不能解释出答题原理。所以在二次函数的教学中，教师要不断强调基本概念，让学生对基本概念烂熟于心，才能在解题的过程中正确运用。在讲解的过程中，教师可以列举一些实例来说明形似y= ax2+bx+c（a≠0）的函数是二次函数。另外，要让学生铭记：给出任意的x值都会产生相对应的y值，这就表明y是x的二次函数，这个关系式不是简单的一个等式，而是通过一个未知数来表示另一个未知数。因此，使学生在理解方程概念的基础上深入理解有关函数的概念。

在学习二次函数的时候，很多学生会发现这部分的知识和其他相关知识很相似，碰到问题的时候，无法确定到底需要运用哪些知识，就不能列出正确的式子求解。所以，教师在教学的过程中，要将类似的问题区分开，使抽象的问题具体化，使学生明确学习方向。例如，在教学过程中，二次函数的题目不仅是简单的二次函数，还会包含一元二次方程、一次函数、反比例函数等内容，学生很容易将这些内容混淆，所以教师要通过不同类型的具体题目进行讲解，帮助学生排除干扰因素，归纳出正确的解题思路。

三、培养学生的识图观察能力，运用数形结合进行教学

在学习二次函数的过程中，图象的作用是十分重要的，能够快速、准确地识图，对学生识别数学公式，快速、有效地解开题目有着重要的作用。教师要培养学生识图观察的能力，让学生在学习之后能够做到看到函数式就能想到对应的图象，在看到图象之后也能想到相应的关系式，运用数形结合更好地进行解题。在训练学生识图的时候，可以运用情景教学法让学生体会二次函数图象的含义，以及比较不同的函数抛物线各有怎样的特点。在这个过程中，要让学生去主动探索，激发他们主动学习的热情，同时锻炼动脑和动手的能力。

例如，在同一个直角坐标系中，画出y=2x2以及y=-2x2的图象，并比较这两个图象有哪些共同点，有哪些不同点。在解题的过程中，首先让学生画出这两个函数的图象，如图1：

图1

之后让学生进行思考并发言，找出它们的异同点。不难发现，二者的共同点是他们都是二次函数，都以y轴为对称轴，顶点都是坐标原点，图象都是抛物线。而二者的不同点也很容易进行比较，首先，y=2x2的图象的开口是向上的，顶点是抛物线的最低点，对称轴的左边，抛物线由左上向右下延伸，右边是由左下向右上延伸。y=-2x2的图象恰恰相反，它的开口是向下的，顶点是整个抛物线的最高点，对称轴的左边图象是由左下向右上延伸，而在对称轴的右边，图象是由左上向右下延伸的。这个例题的作用就是让学生先通过自己动手画出函数的图象，并通过自己的观察得到结论。掌握了这种最基本的函数图象之后，学生就能较容易地掌握比较复杂的函数图象，在遇到问题时，也能通过图象帮助解题。

四、结合生活实际，鼓励学生不断创新

学习数学知识的根本目的是要在日常生活中运用这些知识，尤其是类似二次函数这样的知识，在生活中有着极其广泛的运用，就更需要教师把二次函数融入到实际生活当中，使学生能够活学活用。用所学的知识解决实际问题，也能使学生学习的成就感提升，激发他们更深一步学习的热情，实现学以致用。

例如，在工程施工的过程中，经常需要挖出涵洞来配合工程，现有一处涵洞，形状是抛物线形，它的截面如图2所示，现在测量得水面的宽度为1.6米，涵洞的顶点O到水面的距离是2.4米，在如图所构建的直角坐标系内，试求出涵洞所在的抛物线的函数关系式。

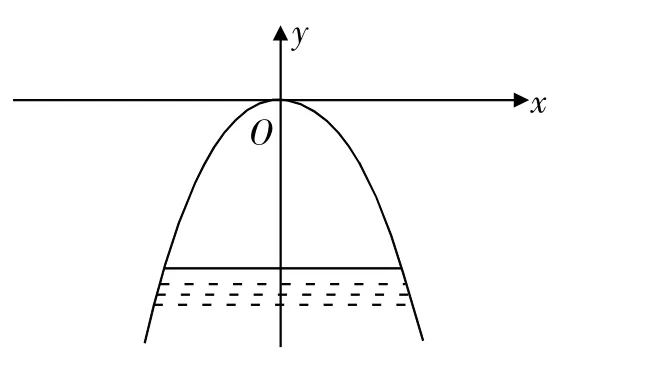
图2

通过这些实际问题，可以锻炼学生将文字转化为数学语言的能力，也能使学生将课堂的学习和实际生活联系到一起，增强数学学习的实效性，让学生爱上数学。

除了在教学过程中联系实际外，还应该培养学生在数学学习中的创新能力。数学不是死板的知识，通过不同知识的组合，能够产生新的解题方法和研究思路。所以在教学过程中，教师应该把学习的主体位置让给学生，认识到自己在教学过程中起到的只是辅助作用。在教学实践的过程中，可以让学生扮演老师的角色，为同学进行讲解，锻炼学生对知识的理解能力、语言的组织能力和表达能力，老师在旁边仔细聆听，记录学生存在的问题再反馈给学生，对学生的不足之处进行指导。这样的教学方式不仅能够加深学生对知识的理解，更能锻炼学生的学习能力。

二次函数是初中数学的重要教学内容，要使学生能够完全掌握这部分知识，就要让学生成为课堂的主人，充分调动学生的学习积极性，让每位学生都参与到对知识的探讨之中。在学习的过程中，不能急于求成，要从最基础的知识抓起，不断提高难度，在巩固旧识的基础上学习新知。

（编辑：杨 迪）

G633.6

A

1671-0568（2015）33-0085-02