双参数指数型分布最小和最大次序统计量矩的精确计算公式

刘 宣

(福州大学 阳光学院 基础部 福建 福州 350015)



双参数指数型分布最小和最大次序统计量矩的精确计算公式

刘 宣

(福州大学 阳光学院 基础部 福建 福州 350015)

讨论双参数指数型分布最小和最大次序统计量矩的计算，利用双参数指数型分布矩的递推关系及密度函数的特点获得了它的最小和最大次序统计量各阶矩以及各阶混合矩的精确计算公式．

双参数指数型分布； 次序统计量； 矩

0 引言

次序统计量是统计理论与应用中常用的一种统计量，有关其矩的计算问题是人们感兴趣的课题．然而，由于一般次序统计量分布的复杂性，使得其高阶矩计算十分困难，并不是任意总体的次序统计量的高阶矩都能获得精确简单的计算公式，但已有部分结果，如文献[1-4]．本文考虑了一个特殊的总体—双参数指数型分布总体次序统计量矩的计算问题，获得了它的最小和最大次序统计量高阶原点矩和混合矩的精确计算公式．

双参数指数型分布是可靠性工程中一种有用的失效分布，常用于描述伺服机构、车辆、电子产品等的寿命分布，具有重要的应用价值，它的密度函数和分布函数分别为[5]：

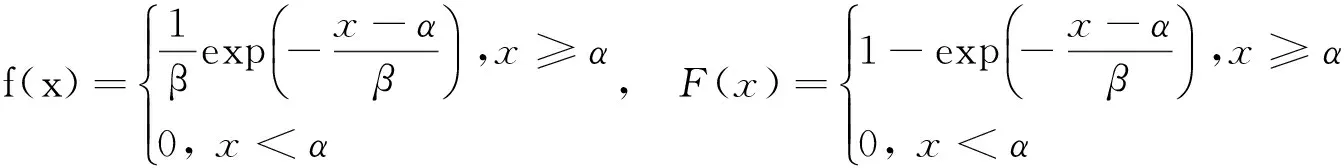
其中,α∈R称为门限参数，β∈R+称为尺度参数．

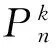
1 引理

引理1[5]若{Xn:1≤k≤n}是来自某总体的一个样本，该总体具有密度函数f(x)和分布函数F(x)，X(1),X(2),…,X(n)为其次序统计量，则

1) X(1)的密度函数为

f1(x)=n[1-F(x)]n-1f(x)；

2) X(n)的密度函数为

fn(x)=nFn-1(x)f(x)；

3) (X(1),X(n))的密度函数为

引理2若随机变量X服从门限参数为α、尺度参数为β的双参数指数型分布，则X的k阶原点矩为

证明由随机变量k阶原点矩的定义可知

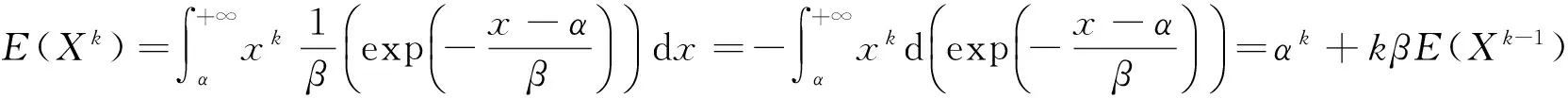
2 主要结论

定理1若{Xk:1≤k≤n}是来自参数为α∈R，β∈R+的双参数指数型分布总体的一个样本，X(1),X(n)为其最小和最大次序统计量，则

1) X(1)的密度函数为

2) X(n)的密度函数为

3) (X(1),X(n))的密度函数为

证明由引理1及双参数指数型分布的密度函数和分布函数立即可得此结论．

② 最大次序统计量已不服从双参数指数型分布，但其密度函数可看做不同双参数指数型分布密度函数的线性组合．

定理2若{Xk:1≤k≤n}是来自参数为α∈R，β∈R+的双参数指数型分布总体的一个样本，X(1),X(n)为其最小和最大次序统计量，则

1)

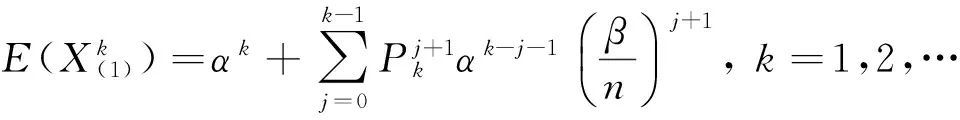
2)

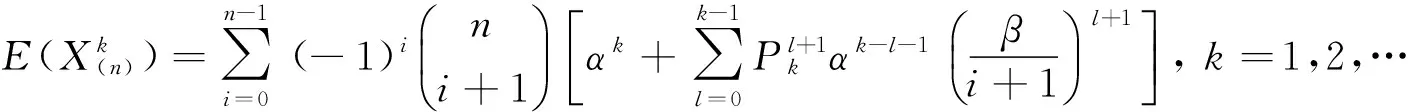
3)

证明1) 由定理1的注①及引理2可证．

2) 由定理1的2)及引理2可知

故结论(2)成立．

3) 由定理1的3)及引理2可得

注由上可知，E(X(1))≠E(X(n))，E(X(1)X(n))≠E(X(1))E(X(n))．因此，若{Xk:1≤k≤n}是来自参数为α∈R，β∈R+的双参数指数型分布总体的一个样本，X(1),X(2),…,X(n)为其顺序统计量，则X(1),X(2)-X(1),…,X(n)-X(n-1)既不独立也不同分布．

3 应用

定义1若{Xn:1≤k≤n}是来自某总体的一个样本，X(1),X(2),…,X(n)为其次序统计量，则称Rn=X(1)-X(n)为样本极差．

样本极差可以反映总体分布的变异范围和离散程度，在质量控制分析中有广泛应用．如对于某产品的某项指标，当生产处于稳定状态时，可通过设定置信水平得到这项指标取值的控制区间.在实际应用时通常每次都要计算样本均值与方差，计算较繁琐，且为了保证样本均值和方差计算的准确性，做检查时必须逐个检查样本观察值．若对检验结果有疑问则需要加大样本容量，一些计算又得重新进行.在高度自动化的现代工业生产条件下，这种做法对检验生产过程是否正常等及时作出判断是很不适应的[6]，而样本极差在一定程度上可以弥补上述缺陷，计算相对简捷，因此可用于质量控制，但这个过程通常需要求出样本极差的期望和方差．

假设根据以往的生产经验，某产品的某项指标X服从门限参数为α、尺度参数为β的双指数分布，{Xn:1≤k≤n}为抽取的样本，下面求出此样本极差的期望和方差．

由于样本极差的分布较复杂，因此不宜用此分布函数去求．直接利用本文定理2所得结论计算可得,

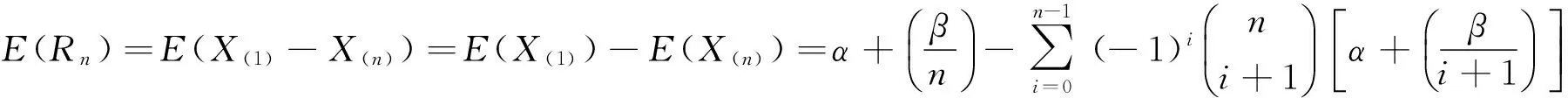
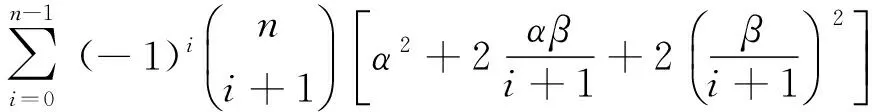
4 结论

综上，本文获得了双参数指数型分布总体最小和最大次序统计量各阶原点矩以及各阶混合矩的精确计算公式．从公式的形式上看没有积分运算，稍微复杂一点不过是有限项求和，用数学软件容易实现比较精确的计算结果，因此在质量分析中具有一定的应用价值． 当然，任意总体次序统计量矩的计算问题较复杂，有待进一步研究．

[1]ChildsA．HigherordermomentsoforderstatisticsfromINIDexponentialrandomvariables[J]．StatisticalPapers，2003，44(2)：151-167．

[2]ThomasPY，SamuelP．Recurrencerelationforthemomentsoforderstatisticsfromabetadistribution[J]．StatisticalPapers，2008，49(1)：139-146．

[3] 张金延．次序统计量矩的计算[J]．中国科学院研究生院学报，1990，7(1)：1-29．

[4]NadarajahS．Explicitexpressionsformomentsoforderstatistics[J]．Statistics&ProbabilityLetters，2008，78(2)：196-205．

[5] 茆诗松，王静龙，濮晓龙．高等数理统计[M]．2版.北京：高等教育出版社，2006．

[6] 张方仁．极差的概率分布和它在质量控制中的应用[J]．数学的实践与认识，1985，15(3)：4-14．

(责任编辑：王浩毅)

Precise Calculation Formula of the Minimum and Maximum Order Statistic Moments of Two-parameter Exponential Distribution

LIU Xuan

(FoundationDepartment,FuzhouUniversitySunshineCollege，Fuzhou350015，China)

The calculation of the minimum and maximum order statistic moments of two-parameter exponential distribution was discussed． The moments and mixed moments precise calculation formula of two-parameter exponential distribution were obtained by using the recursive relations of moments and the characteristics of the density function of two-parameter exponential distribution．

two-parameter exponential; order statistic; moment

2014-12-19

福建省教育厅资助项目，编号JB13262．

刘宣(1982-)，男，湖南耒阳人，讲师，硕士，主要从事随机过程研究， E-mail: liuxuanyg@163.com．

刘宣. 双参数指数型分布最小和最大次序统计量矩的精确计算公式[J].郑州大学学报：理学版，2015，47(2)：41-44.

O212．1

A

1671-6841(2015)02-0041-04

10.3969/j.issn.1671-6841.2015.02.009