关于Diophantine方程x3±1=2pqry2

管训贵

(泰州学院 数理学院 江苏 泰州 225300)



关于Diophantine方程x3±1=2pqry2

管训贵

(泰州学院 数理学院 江苏 泰州 225300)

设p,q,r为奇素数，p≡13 mod 24，q≡19 mod 24，(p/q)=-1.利用同余式、平方剩余、递归序列、Legendre符号的性质、Pell方程解的性质等证明了：(A) 若r≡5 mod 12，则方程G：x3-1=2pqry2仅有平凡解(x,y)=(1,0)；若r≡11 mod 12，则方程G最多有2组正整数解. (B) 若r≡11 mod 12，则方程H：x3+1=2pqry2仅有平凡解(x,y)=(-1,0)；若r≡5 mod 12且(pq/r)=-1，则方程H最多有2组正整数解.

Diophantine方程； 奇素数； 整数解； 递归序列； 同余式； 平方剩余； Legendre符号

0 引言

设D>0且不是平方数.熟知，方程

x3±1=Dy2

(1)

是一类基本而又重要的三次Diophantine方程，其整数解已有不少学者研究过[1-8].

本文就D含素因数2和一个6k-1形的素因数及两个互异的6k+1形的素因数的情形给出以下一般性的结果：

定理1设p,q,r为奇素数，p≡13 mod 24，q≡19 mod 24，(p/q)=-1.若r≡5 mod 12，则Diophantine方程

x3-1=2pqry2

(2)

仅有平凡解(x,y)=(1,0)；若r≡11 mod 12，则(2)最多有2组正整数解.

定理2设p,q,r为奇素数，p≡13 mod 24，q≡19 mod 24，(p/q)=-1.若r≡11 mod 12，则Diophantine方程

x3+1=2pqry2

(3)

仅有平凡解(x,y)=(-1,0)；若r≡5 mod 12且(pq/r)=-1，则(3)最多有2组正整数解.

1 引理

引理1若r≡5 mod 6为奇素数，则x2+x+1≢0 modr.

证明假定x2+x+1≡0 modr，则(2x+1)2≡-3 modr，即Legendre符号值(-3/r)=1，由此推出r≡1 mod 6，与r≡5 mod 6矛盾.证毕.

引理2设a,b,r为奇素数，则方程

x-1=2aru2;x2+x+1=bv2;y=uv;gcd(u,v)=1.

(4)

当a≡1 mod 12，b任取，(a/b)=-1；或r≡5 mod 12，a≡7 mod 12，b≡5,7 (mod 8)时无整数解.

证明将x-1=2aru2代入x2+x+1=bv2，得(4aru2+3)2+3=4bv2，两边取模a得，3≡bv2moda.若a≡1 mod 12，则Legendre符号值(3/a)=1，又Legendre符号值(bv2/a)=(b/a)=-1，矛盾，故此时方程(4)无整数解；由u2≡0,1,4(mod 8)知，x=2aru2+1≡1,2ar+1(mod 8)，因v为奇数，r≡5 mod 12，故b≡3,2a+3(mod 8)，若a≡7 mod 12，则b≡3,1(mod 8)，与b≡5,7(mod 8)矛盾，故此时方程(4)仍无整数解.

引理3[9]设p是一个奇素数，则Diophantine方程4x4-py2=1除p=3,x=y=1和p=7,x=2,y=3外，无其他的正整数解.

引理4[10]方程

x2-Dy4=1(D>0且不是平方数)

(5)

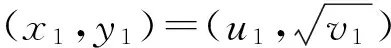
2 定理的证明

先证定理1.

证明因为奇素数r≡5 mod 6，根据引理1，x2+x+1≢0 modr，又gcd(x-1,x2+x+1)=1或3，且x2+x+1≢0 mod 2，故方程(2)给出以下8种可能的分解情形：

情形Ⅰx-1=2pqru2，x2+x+1=v2，y=uv，gcd(u,v)=1；

情形Ⅱx-1=2ru2，x2+x+1=pqv2，y=uv，gcd(u,v)=1；

情形Ⅲx-1=2pru2，x2+x+1=qv2，y=uv，gcd(u,v)=1；

情形Ⅳx-1=2qru2，x2+x+1=pv2，y=uv，gcd(u,v)=1；

情形Ⅴx-1=6pqru2，x2+x+1=3v2，y=3uv，gcd(u,v)=1；

情形Ⅵx-1=6ru2，x2+x+1=3pqv2，y=3uv，gcd(u,v)=1；

情形Ⅶx-1=6pru2，x2+x+1=3qv2，y=3uv，gcd(u,v)=1；

情形Ⅷx-1=6qru2，x2+x+1=3pv2，y=3uv，gcd(u,v)=1．

下面分别予以讨论．

情形Ⅰ时，解x2+x+1=v2，得x=0,-1，均不适合x-1=2pqru2，故该情形方程(2)无整数解．

情形Ⅱ时，由u2≡0,1,4(mod 8)知，x=2ru2+1≡1,2r+1(mod 8)，因v为奇数，故pq≡pqv2=x2+x+1≡3,(2r+1)2+2r+2≡3,2r+3(mod 8).若r≡5 mod 12，则pq≡3,5(mod 8)；若r≡11 mod 12，则pq≡1,3(mod 8).但由p≡13 mod 24，q≡19 mod 24知，pq≡7 mod 8，矛盾，故该情形方程(2)无整数解．

情形Ⅲ时，因p≡13 mod 24，故p≡1 mod 12，又(p/q)=-1，根据引理2知,该情形方程(2)无整数解．

情形Ⅳ时，因q≡19 mod 24，p≡13 mod 24，故q≡7 mod 12，p≡5 mod 8，根据引理2知,该情形方程(2)无整数解．

情形Ⅴ时，将x-1=6pqru2代入x2+x+1=3v2，整理得

(2v)2-3(4pqru2+1)2=1，

(6)

故方程(6)的一切整数解可表示为

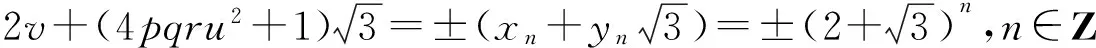
4pqru2=yn-1．

(7)

由(7)得yn≡1 mod 4．

容易验证下列各式成立：

xn+2=4xn+1-xn;x0=1;x1=2,

(8)

yn+2=4yn+1-yn;y0=0;y1=1,

(9)

x2n≡1,7(mod 8);x2m+1≡2 mod 4;y2m≡0 mod 4,

(10)

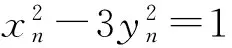
(11)

xn+1=2xn+3yn;yn+1=xn+2yn,

(12)

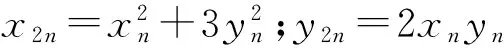
(13)

对递归序列(9)取模4，得周期为4的剩余类序列，且当n≡-1 mod 4时，有yn≡-1 mod 4；当n≡1 mod 4时，有yn≡1 mod 4，所以仅当n≡1 mod 4时式(7)才成立．

2pqru2=x2m+1y2m．

(14)

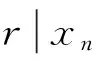
考虑到gcd(x2m+1,y2m)=gcd(2x2m+3y2m,y2m)=gcd(2x2m,y2m)=gcd(2,y2m)=2.由式(10)知，x2m+1≡2 mod 4，y2m≡0 mod 4，且x2m+1≢0 modr，所以(14)可分解为以下4种可能的情形：

情形Ax2m+1=2a2，y2m=4pqrb2，u=2ab，gcd(a,b)=1；

情形Bx2m+1=2pqa2，y2m=4rb2，u=2ab，gcd(a,b)=1；

情形Cx2m+1=2qa2，y2m=4prb2，u=2ab，gcd(a,b)=1；

情形Dx2m+1=2pa2，y2m=4qrb2，u=2ab，gcd(a,b)=1．

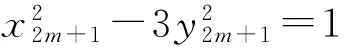
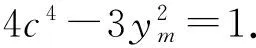
若情形C成立，则由x2m+1=2x2m+3y2m得2qa2=2x2m+12prb2，即qa2=x2m+6prb2.因a,b均为奇数，故q≡x2m-2pr(mod 8)，即x2m≡q+2pr(mod 8)，由式(10)知，x2m≡1,7(mod 8)，从而有q+2pr≡1,7(mod 8).当r≡5 mod 12，p≡13 mod 24，q≡19 mod 24时，q+2pr≡5 mod 8，矛盾.此时情形C不成立. 当r≡11 mod 12时，由y2m=4prb2得xmym=2prb2，又xm≢0 modr，ym≢2 mod 4,而gcd(xm,ym)=1，所以下列情形之一成立：

xm=2c2;ym=prd2;b=cd;gcd(c,d)=1,

(15)

xm=2pc2;ym=rd2;b=cd;gcd(c,d)=1．

(16)

若情形D成立，则由情形C的讨论知p+2qr≡1,7(mod 8)，当r≡5 mod 12，p≡13 mod 24，q≡19 mod 24时，q+2pr≡3 mod 8，矛盾.此时情形D不成立. 当r≡11 mod 12时，仿情形C的r≡11 mod 12的情况知，该情形方程也最多有1组正整数解.

情形Ⅵ时，仿情形Ⅱ的讨论知，该情形方程(2)无整数解．

情形Ⅶ时，将x-1=6pru2代入x2+x+1=3qv2，得3(4pru2+1)2+1=4qv2，两边取模p得，1≡qv2modp，但Legendre符号值(q/p)=(p/q)=-1，故该情形方程(2)无整数解．

情形Ⅷ时，仿情形Ⅶ的证明,再根据Legendre符号值(p/q)=-1可得方程(2)无整数解．

综上所述，定理1成立．

类似可证定理2成立.

[1] 柯召，孙琦．关于丢番图方程x3±1=Dy2[J]．中国科学，1981,24(12)：1453-1457.

[2] 柯召，孙琦．关于丢番图方程x3±1=3Dy2[J]．四川大学学报：自然科学版，1981,18(2)：1-5.

[3] 杜先存，管训贵，万飞．关于不定方程x3-1=3pqy2的整数解[J]．郑州大学学报：理学版，2014,46(3)：44-47.

[4] 黄寿生．关于指数Diophantine方程x3-1=2py2[J]．数学研究与评论，2007, 27(3)：664-666.

[5] 罗明，黄勇庆．关于不定方程x3-1=26y2[J]．西南大学学报：自然科学版，2007,29(6)：5-7.

[6] 杜先存，管训贵，杨慧章．关于不定方程x3+1=91y2[J]．内蒙古师范大学学报：自然科学汉文版，2013，42(4)：397-399.

[7] 杜先存，万飞，杨慧章．关于丢番图方程x3±1=1 267y2的整数解[J]．数学的实践与认识，2013，43(15)：288-292.

[8] 管训贵，杜先存．关于Diophantine方程x3±1=pqy2[J]．安徽大学学报：自然科学版，2014，38(1)：29-35．

[9] 曹珍富．丢番图方程引论[M]．哈尔滨：哈尔滨工业大学出版社，1989：20-69．

[10]Walsh P G. A note on a theorem of Ljunggren and the Diophantine equationx2-kxy2+y4=1,4[J]．Arch Math Basel,1999,73(2):119-125.

(责任编辑：王海科)

On the Diophantine Equationx3±1=2pqry2

GUAN Xun-gui

(SchoolofMathematicsandPhysics,TaizhouUniversity,Taizhou225300,China)

Letp,q,rbe odd primes withp≡13 mod 24,q≡19 mod 24, (p/q)=-1. By using congruence, quadratic residue, recursive sequence，some properties of Legendre symbol and the solutions to Pell equation, the following theorem was proved: (A) ifr≡5 mod 12, then the equation G:x3-1=2pqry2only has trivial solution (x,y)=(1,0); ifr≡11 mod 12, then the equation G have at most two positive integer solutions (x,y). (B) ifr≡11 mod 12, then the equation H:x3+1=2pqry2only has trivial solution (x,y)=(-1,0); ifr≡5 mod 12 and (pq/r)=-1,then the equation H has at most two positive integer solutions (x,y).

Diophantine equation; odd prime; integer solution; recursive sequence; congruence; quadratic remainder； Legendre symbol

2015-01-19

江苏省教育科学“十二五”规划课题资助项目，编号D201301083；泰州学院重点课题资助项目，编号TZXY2014ZDKT007；云南省教育厅科研项目，编号2014Y462.

管训贵(1963-)，男，江苏兴化人，副教授，主要从事初等数论研究,E-mail:tzszgxg@126.com.

管训贵.关于Diophantine方程x3±1=2pqry2[J]. 郑州大学学报：理学版，2015,47(2)：49-52.

O156

A

1671-6841(2015)02-0049-04

10.3969/j.issn.1671-6841.2015.02.011