基于经典风险模型的最优分红和最优注资策略研究

王永茂， 祁晓玉， 贠小青

(1.燕山大学 理学院 河北 秦皇岛 066004； 2.燕山大学 里仁学院 河北 秦皇岛 066004)



基于经典风险模型的最优分红和最优注资策略研究

王永茂1， 祁晓玉1， 贠小青2

(1.燕山大学 理学院 河北 秦皇岛 066004； 2.燕山大学 里仁学院 河北 秦皇岛 066004)

基于经典风险模型，对有限分红率下公司分红和注资的最优策略进行了深入研究，以便实现公司风险最小化或者股东净收益最大化的目的.首先根据保险公司的盈余过程推导了值函数V(x)的具体表达式，证明了值函数V(x)具有的某些性质，然后建立V(x)满足的HJB方程，通过对方程的研究得到保险公司最优分红和最优注资策略，并给出了最优注资上限和最优注资下限.最后对公司面临破产风险时是否选择注资以及注资量大小进行了探讨.

经典风险模型； 分红策略； 注资策略； HJB方程

0 引言

随着保险市场的高速发展，策略由分红开始逐步拓展到注资、再保险等领域.公司一般通过控制某些组合策略来满足预定的目标函数，从而得到最优的分红策略和注资策略，使公司的破产风险达到最小，或者使股东的利益达到最大.在经典风险模型下，文[1-2]认为随机控制问题很难找到清晰解，只能在阂值策略中寻求最优解.文[3]研究了资产注入过程的最优控制问题，文[4]对保险效用最大化理论进行了分析，文[5]给出了最优分红值的估计方法，文[6]对二项风险模型进行了研究，文[7]进一步研究了分红控制过程的最优停止问题.

本文基于经典风险模型，对有限分红率下公司分红和注资的最优策略进行了研究.

1 模型建立

设t时刻，保险公司盈余表示为

其中，x∈R为初始准备金，c>0为保费收入率，{Ui,i≥1}是一列正的且相互独立同分布的实际变量序列，表示第i次索赔的大小，分布函数为F(x)，{Nt,t≥0}为索赔计数过程，是一个参数为λ>0的Possion过程，{Ui,i≥1}和{Nt,t≥0}相互独立.假设EUi=μ<∞且F(x)连续.{Xt}在空间(Ω，F，{Ft}t≥0，P)上，Ex和Px代表初值为x的期望和概率.

用{Dt}和{Zt}表示截止到t时刻的累积分红和累积注资，在原模型的基础上，本文引入策略π={(Dt,Zt)}:

1) {Dt}是右连续的具有左极限的增的适应过程，满足D0-=0；

2) {Zt}是左连续的具有右极限的增的适应过程，满足Z0=0.

则新的盈余过程可以表示为

目标函数是最大化股东的折现分红与折现注资二者之差的期望值，即股东的净收益.因此，定义π对应的值函数为

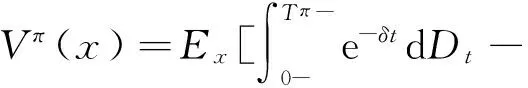
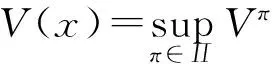
2 值函数V(x)的性质

定理1如果定义注资策略为

那么对于x∈R+，在任意可能的分红策略下，值函数都有下界-φλμ/δ.

证明在定理1定义的注资策略假设下，公司破产的时刻为∞.股东可能承担一切索赔，如果不考虑分红，这时的值函数达到最小.第k个索赔的到达时刻Tk服从Γ(λ,k)分布，则

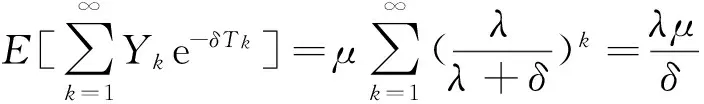
所以值函数有下界-φλμ/δ.

定理2V(x)在(-∞，+∞)上是增的Lipschitz连续的函数，并且

证明V(x)是增函数是显然的.当x<0时，若定义策略π：Zt=Ut=0，则V(x)≥Vπ(x)=0.因为V(x)是增函数，所以V(x)≥0，x∈R.若Zt=0，Ut=u0,则

(1)

由定理1，则

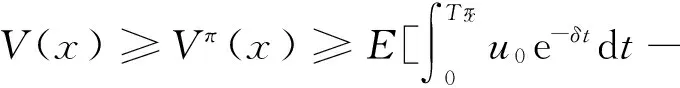
当x≥0时，令h>0充分小，定义

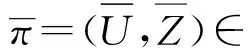
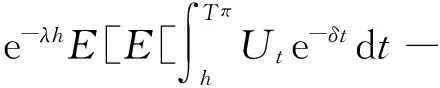
因此

根据V(x)的有界性，

0≤V(x+ch)-V(x)≤V(x+ch)(1-e-(λ+δ)h)≤

V(x+ch)(λ+δ)h≤u0δ-1(λ+δ)h.

当x<0时，股东注资h后，应用最优策略，则

V(x)≥V(x+h)-φh，

即V(x+h)-V(x)≤φh,由此可证明V(x)在(-∞,+∞)上的Lipschitz连续性.

3 HJB方程和最优策略

c为保费收入率，u表示分红率，δ,φ分别表示折现因子和罚金因子，由文[8]以及V(x)满足的动态规划原理,

可以得到V(x)在[0,∞]上满足的Hamilton-Jacobi-Bellman方程为

(2)

首先，由于u(1-V′(x))关于u是线性的，最大化u(1-V′(x))的u*为

若V(x)在[0,∞]是凹的，那么存在最优分红限b=inf{x:V′(x)≤1}满足

并且存在边界a0=sup{x,V′(x)≥φ}.若盈余小于a0，根据z*，股东会采取如下策略：

1) 若赤字大于z*，股东选择拒绝注资，公司破产；

2) 若赤字小于z*，如果注资，就必须让盈余过程恢复a0.若a0<0，注资不会使公司摆脱破产.

综上考虑，本文定义注资上限为a=a0∨0.

4 结论

由于经典风险模型具有索赔不确定性，索赔很大时很可能会产生赤字，因此每一次注资都相当于投资，投资能不能得到合理的回报，就要股东进行判断，选择出最佳的注资策略. 用b表示最优分红限，若值函数V(x)在[0,∞]是凹的，那么对于股东来说，最优策略是公司盈余在(0，b)上，不采取分红和注资.若超出了b，公司就要以最大分红率u0对股东进行分红.公司发生赤字时，如果赤字小于z*，股东应选择注资至0点，使公司继续经营，而如果赤字超过z*，就无需注资，公司选择破产.

[1] Bäuerle N. Approximation of optimal reinsurance and dividend payout policies[J]. Mathematical Finance, 2004, 14(15): 99-113.

[2] Schmidli H. Stochastic Control in Insurance[M]. London: Springer, 2008.

[3] Eisenberg J, Schmidli H. Optimal control of capital injections by reinsurance in a diffusion approximation[J]. Blätter der DGVFM, 2009, 30(1): 1-13.

[4] 吕会茹，王永茂，管巍，等.基于效用最大化理论关于保险人监管成本的分析[J].郑州大学学报：理学版，2011，45(1): 42-45.

[5] Xu Huai, Tang Ling. Approximations of the optimal dividends barrier in classical risk model[J]. Mathematica Applicate, 2011, 24(3): 512-518.

[6] 刘超，王永茂，颜玲，等.带干扰的多险种二项风险模型的破产概率[J].郑州大学学报：理学版，2012，44(1): 46-49.

[7] 李岩，刘国新.经典风险模型分红控制过程的最优停止问题[J].应用数学学报,2010, 33(6): 1121-1132.

[8] Schmidli H, Scheer N. Optimal dividend strategies in a Cramer-Lundberg model with capital injections and administratin costs[D]. Germany: University of Cologne，2011.

(责任编辑：王海科)

Optimal Dividend and Capital Injection Strategy in Classical Risk Model

WANG Yong-mao1， QI Xiao-yu1， YUN Xiao-qing2

(1.DepartmentofScience,YanshanUniversity,Qinhuangdao066004,China;2.CollegeofLiren,YanshanUniversity,Qinhuangdao066004,China)

Based on the classical risk model, the optimal dividend and injection were studied to minimize the risks for the company or maximize the shareholder’s profit when the dividend was restricted. Firstly, the surplus process of insurance company was explored, and the value functionV(x) was presented. Secondly, some properties of the value functionV(x) were examined, then the HJB equations were established. And the optimal dividend and capital injection strategies were found. At the same time, the capital injection boundary was put forward. Finally, whether to inject and the amount of injection were discussed when facing the risk of bankruptcy.

classical risk model; dividend strategy; capital injection strategy; HJB equation

2015-01-13

王永茂(1958-)，男，河北阜城人，教授，主要从事保险风险分析、金融数学研究，E-mail:mrymw@ysu.edu.cn；通讯作者：祁晓玉(1988-)，女，河北石家庄人，硕士研究生，主要从事寿险精算研究，E-mail:qxysjz@sina.com.

王永茂，祁晓玉，贠小青. 基于经典风险模型的最优分红和最优注资策略研究[J].郑州大学学报：理学版，2015,47(2)：37-40.

F842.62

A

1671-6841(2015)02-0037-04

10.3969/j.issn.1671-6841.2015.02.008