Banach空间中一类奇异积分边值问题解的存在性

汪子莲， 丁 珂

(1.兰州工业学院 基础学科部 甘肃 兰州 410075;2.伊利诺伊大学香槟分校 数学学院 美国 诺伊州 香槟 450001)



Banach空间中一类奇异积分边值问题解的存在性

汪子莲1， 丁 珂2

(1.兰州工业学院 基础学科部 甘肃 兰州 410075;2.伊利诺伊大学香槟分校 数学学院 美国 诺伊州 香槟 450001)

运用Sadovskii不动点定理讨论了Banach空间中一类二阶奇异积分边值问题解的存在性，获得了此类问题解存在的充分性条件.

积分边值问题； Sadovskii不动点定理； 非紧性测度； 存在性

0 引言

带有积分边界条件的常微分方程边值问题产生于应用数学及物理学的不同领域.热传导、化学工程等领域中的许多模型都可归为带有积分边界条件的微分[1-2].

带有积分边界条件的边值问题是一类十分有趣且重要的研究课题，其包含两点、三点、多点等多种类型的边值问题，且以这些边值问题为特例[3-7].实数空间中积分边值问题解的存在性被许多学者研究过.但是，迄今为止，对Banach空间中带有积分边界条件的边值问题的研究却极少.为此，本文将运用Sadovskii不动点定理研究Banach空间中一类带有积分边界条件的二阶非线性常微分方程边值问题解的存在性.

文[8]研究了二阶三点边值问题

(1)

解的存在性，其中η∈(0,1)，f为一个连续函数.

受文[8]的启发，本文考察积分边值问题

(2)

或者

(3)

解的存在性，其中f∈C(I×E×E,E),I=[0,1],θ是Banach空间(E,‖·‖)中的零元素，g∈L1[0,1]且非负，h∈C((0,1),[0,+∞))，在t=0和t=1处有奇性.

注1本文将文[8]的结果推广到积分边值问题，并且考虑了h在t=0及t=1处奇异的情形.

注2当g≡0,h≡1且非线性项f不含一阶导项时，边值问题(2)、(3)就退化为文[9]研究的问题.

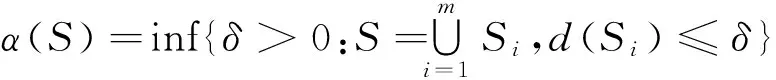
定义2[10]设E1,E2是实Banach空间，D⊂E,设A:D→E2有界连续.

(ⅰ)如果存在常数k≥0，使得对任意有界集S⊂D,都满足α(A(S))≤kα(S),则称A是D上的k-集压缩映象.特别地，当k<1时的k-集压缩映象称为严格集压缩映象.

(ⅱ)如果对任意非相对紧的有界集S⊂D都满足α(A(S))<α(S),则称A是D上的凝聚映象.

显然，若A是一个严格集压缩映象，则A是凝聚映象.

引理1[10]若H⊂C[I,E]有界且等度连续，则α(H(t))于I连续且

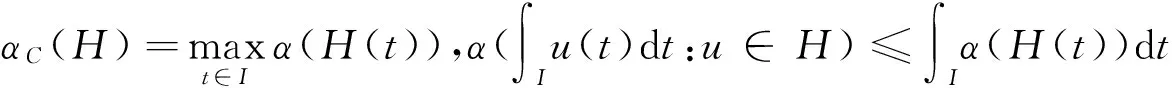
其中αC(·),α(·)分别表示H⊂C[I,E]及H(t)⊂E的非紧性测度.

引理2[11]设E是实Banach空间，D⊂E为有界凸闭集，若算子A:D→D是凝聚映象，则A于D中有一个不动点.

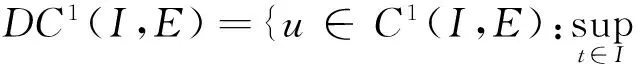
显然，C1(I,E)⊂C(I,E),DC1(I,E)⊂FC(I,E).本文的工作空间为DC1(I,E).记空间E,C(I,E),FC(I,E),DC1(I,E)中的有界集的非紧性测度分别为αE(·),αC(·),αF(·),αD(·).

1 预备知识

为了建立边值问题(2)在DC1(I,E)中解的存在性，本节给出如下假设：

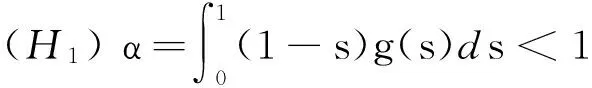
(H2) 存在非负连续函数，a,b,c∈C[0,1]，使得

‖f(t,x,y)‖≤a(t)‖x‖+b(t)‖y‖+c(t),∀t∈I,x,y∈E.

(H3) 对∀r>0,[a,b]⊂I,f(t,x,y)于[a,b]×BE(0,r)×BE(0,r)上一致连续，其中BE(0,r)={u∈E:‖u‖≤r}.

(H4) 存在l1,l2∈L1[0,1]，使得对∀t∈[0,1]及任意有界集D1,D2∈E有

引理3[12]若(H1)成立，则边值问题(2)存在唯一解，

(4)

其中,

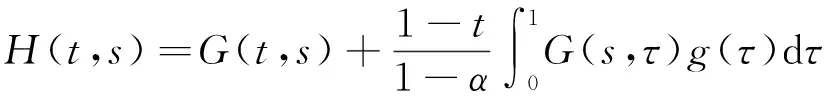
(5)

(6)

对于∀u∈DC1(I,E)，定义算子A,

(7)

引理4若(H1)～(H3)成立，且条件

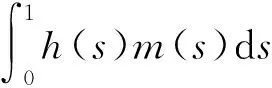
证明由式(7)，(H2),(H5)可知，对∀u∈DC1(I,E),

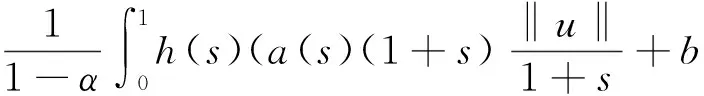
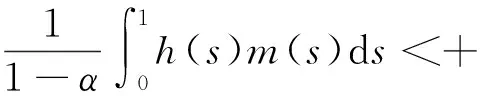
(8)

由式(7)，(H2),(H5)可知

经简单计算可知

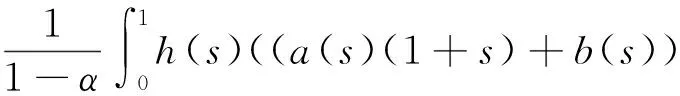
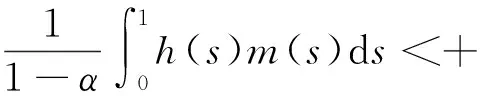
(9)

因此，算子A有定义.

由式(8)，(9)可知，对∀u∈DC1(I,E)都有Au∈DC1(I,E)，所以A于DC1(I,E)有界.

下证算子A于DC1(I,E)连续.

令{un}⊂DC1(I,E),u0∈DC1(I,E),且‖un-u0‖D→0(n→∞).于是存在R>0,使得‖un‖D≤R(n≥1)且‖u0‖D≤R.类似于文[12]，定义hn,

则hn于[0，1]连续，并且，对∀t∈[0,1],hn(t)≤h(t).

定义算子An，

(10)

显然，对∀u∈DC1(I,E)，有Anu∈DC1(I,E),且An连续，事实上，

由条件(H3)知，对∀s∈[0,1],∃N1>0,对∀n≥N1,有

(11)

所以

‖(Anun)(t)/(1+t)-(Anu)(t)/(1+t)‖≤(1/(1+t))·(ε/3)<ε/3.

(12)

同时，对∀ε>0,∀t∈[0,1]及n≥N1有

‖(Anun)′(t)-(Anu)′(t)‖≤ε/3.

(13)

由(12)，(13)可知An:DC1(I,E)→DC1(I,E)连续.

由积分的绝对连续性及式(7),(10),(H2),(H5)可知

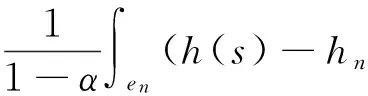
因此，对∀ε>0,∀t∈I,∃N2>0,对∀n≥N2有

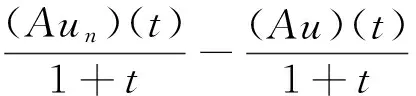
(14)

同理‖(Aun)′(t)-(Au)′(t)‖<ε.

于是，A:DC1(I,E)→DC1(I,E)连续.证毕.

引理5假设(H2)成立，V⊂DC1(I,E)为有界集.则(AV)(t)/(1+t)及(AV)′(t)等度连续.

证明仅需证下列结论成立：

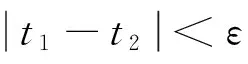
‖(Au)(t2)/(1+t2)-(Au)(t1)/(1+t1)‖<ε.

(15)

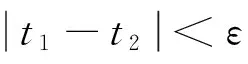
‖(Au)′(t2)-(Au)′(t1)‖<ε.

(16)

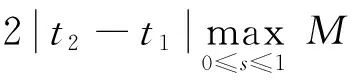
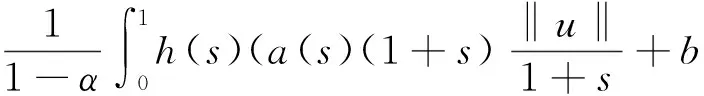
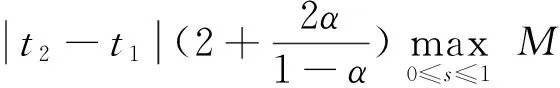
由(H2)可知:

(ⅰ) ‖f(s,u(s),u′(s))‖≤((1+s)a(s)+b(s))‖u‖D+c(s);

(ⅱ) a,b,c∈C[0,1]为非负函数，则于[0,1]有界.假设a(t)≤M1,b(t)≤M2,c(t)≤M3.

对∀t∈[0,1]，令M*=max{M1,M2,M3},由于V有界于DC1(I,E)，所以存在M0>0,使得‖u‖D≤M0,所以，对∀u∈V有

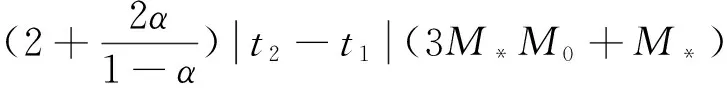
(17)

若t1≥t2,同理可证(AV)(t)/(1+t)于[0,1]等度连续.类似的可证(AV)′(t)于[0,1]等度连续.证毕.

与文献[6]中引理2.5的证明完全类似，可得下面的引理6.

引理6若(H2)成立，V⊂DC1(I,E)为有界子集，则

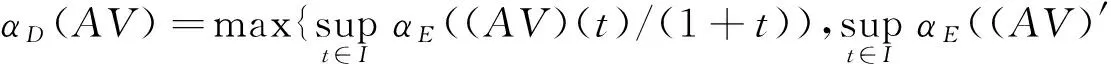
2 边值问题(2)解的存在性

定理1假设(H1)～(H5)成立，则边值问题(2)在DC1(I,E)中至少有一个解.

证明仅需证算子A于DC1(I,E)中有不动点.令

下证A(B)⊂B.

事实上，对∀u∈B，由(7)可知

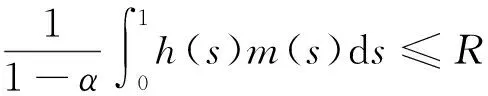
同理可知‖(Au)′(t)‖≤R，于是，由引理4可知A(B)⊂B.

由引理4可知A:Ω→Ω为连续有界算子.下证αD(AV)≤lαD(V),V⊂Ω,其中

事实上，由引理6可知，仅需证

成立即可.

由(H3)及Ω的定义可知{f(s,u(s),u′(s)):u∈V}于[0,1]等度连续.

由(H4)及引理1可知

由t的任意性知

(18)

同理可证

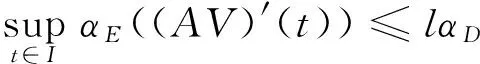
(19)

结合引理6及(18)，(19)可知A:Ω→Ω为严格集压缩算子.显然A是凝聚的.由引理2可知,A于Ω中至少有一个不动点，故边值问题(2)于DC1(I,E)中至少有一个解.证毕.

3 边值问题(2)，(3)解的存在性

现在，考虑边值问题(2)，(3)，由于方法完全类似于第2部分，所以省略本节主要定理的证明.为方便起见，给出如下假设：

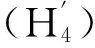
αE(f(t,D1,D2))≤l1(t)αE(D1)+l2(t)αE(D2),

首先，类似于引理3的讨论可知,边值问题(2)，(3)等价于积分方程

(20)

其中,

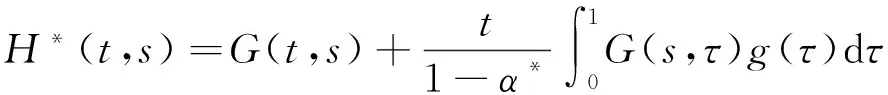
(21)

G(t,s)如(6)定义.

定义算子

(22)

显然，边值问题(2)，(3)有解当且仅当此解是算子A*的不动点.通过与第2部分类似的讨论，有如下结果：

引理8假设(H2)成立，V⊂DC1(I,E)为有界集，则(A*V)(t)/(1+t)及(A*V)′(t)等度连续.

引理9若(H2)成立，V⊂DC1(I,E)为有界集，则

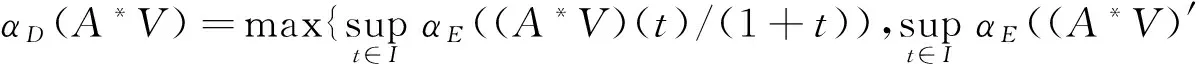
下面给出一个例子来说明结果的正确性.

(23)

定理3无穷维积分边值问题(23)至少有一个解.

取a(t)=l1(t)=t3,b(t)=l2(t)=t3(1+t),c(t)≡0,则容易验证假设条件(H1)～(H5)成立，因此由定理1可知结论成立.证毕.

[1]GallardoJM.Secondorderdifferentialoperaterswithintegralboundaryandgenerationofanalyticsemi-groups[J].RockyMountainJMath,2000,30(4):1265-1292.

[2]KaraKostasGL,TsamatosPC.MultiplepositivesolutionsofsomeFredholmintegralequationsarisefromnonlocalboundaryvalueproblems[J].ElectronJDifferentialEquations,2002(30):1-17.

[3]MaRuyun.Positivesolutionsforanonlinearthree-pointboundaryvalueproblem[J].ElectronJDifferentialEquations,1999(34):1-8.

[4]LiuBing.Positivesolutionsofanonlinearfour-pointboundaryvalueproblemsinBanachspaces[J].JMathAnalAppl,2005,305(1):253-276.

[5]ChenShihua,HuJia,ChenLi,etal.Existenceresultsforn-pointboundaryvalueproblemofsecondorderordinarydifferentialequation[J].JComputApplMath,2005,180(2):425-432.

[6] 梁秋燕.Banach空间分数阶微分方程边值问题解的存在性[J].郑州大学学报：理学版，2013，45(3)：32-36.

[7] 孟宪瑞，曹有好，佟玉霞.奇异Sturm-Liouville边值问题的谱理论[J].郑州大学学报：理学版，2013，45(1)：34-37.

[8]ChenHaibo,LiPeiluan.Existenceofsolutionsofthree-pointboundaryvalueproblemsinBanachspaces[J].MathematicalandComputersModelling,2009,49(3/4):780-788.

[9]GuoDajun,LakshmikanthamV.Multiplesolutionsoftwo-pointboundaryvalueproblemsofordinarydifferentialequationinBanachspaces[J].JMathAnalAppl,1988,129(1):211-222.

[10]GuoDajun,LakshmikanthamV,LiuXinzhi.NonlinearIntegralEquationsinAbstractSpaces[M].Dordrecht:KluwerAcademicPublishers,1996:21-56.

[11]SadovskiiBN.Afixedpointprinciple[J].FunctionalAnalAppl,1967,1(2):151-153.

[12]FengMeiqiang,JiDehong,GeWeigao.PositivesolutionsforaclassofboundaryvalueproblemwithintegralboundaryconditionsinBanachspaces[J].JComputApplMath,2008,222(2):351-363.

(责任编辑：王海科)

Existence of Solutions to a Singular Integral Boundary Value Problem in Banach Spaces

WANG Zi-lian1, DING Ke2

(1.CollegeofBasicCourses,LanzhouPolytechnicCollege,Lanzhou730050,China;2.CollegeofMathematics,UniversityofIllinoisatUrbana-Champaign,Champaign61820,USA)

The existence of solutions for a class of singular second order integral boundary value problems in Banach spaces was discussed by using the Sadovskii fixed point theorem, the sufficient condition for the existence of solutions to such classes of problems was obtained.

integral boundary value problem; Sadovskii fixed point theorem; measure of noncompactness; existence

2014-12-23

汪子莲(1964-)，女，甘肃临夏人，教授，主要从事常微分方程边值问题研究，E-mail:lanyu9986@126.com.

汪子莲，丁珂.Banach空间中一类奇异积分边值问题解的存在性[J].郑州大学学报：理学版，2015，47(02)：13-19.

O175.8

A

1671-6841(2015)02-0013-07

10.3969/j.issn.1671-6841.2015.02.003