通过对比进行学习：多重样例变异性与先前知识的作用*

郭建鹏 杨凌燕

(1厦门大学教育研究院, 厦门 361005) (2美国爱荷华大学教育学院, 爱荷华 52242)

1 问题提出

“样例学习”一直都是教育心理学研究的一个主要课题, 尤其在数学和科学领域得到了许多关注(Atkinson, Derry, Renkl, & Wortham, 2000)。大多数样例学习研究表明, 多重样例的学习效果要好于单个样例, 而且应该并排对比多重样例而不是依次学习每个样例(Alfieri, Nokes-Malach, & Schunn, 2013;Gentner, 2010; Holyoak, 2012; Star et al., 2015)。这是因为通过对比某个概念或原理的多重样例有助于发现类推物之间共同的、深层的结构特征(如对比心脏和水泵), 发展辨别性知识, 促进推理性编码和图式抽象, 并改善日后的迁移和问题解决(Namy & Clepper, 2010; Oakes & Ribar, 2005;Schwartz & Martin, 2004)。Gentner (2005)指出, “对比是一种基本的学习过程, 能够促进深层的联系性学习以及理论性解释的发展” (p.251)。优秀教师善于在数学教学中使用对比来深化学生的认识(Lampert & Cobb, 2003)。很多国家的数学改革也都大力提倡通过样例对比进行教学(e.g., Australian Education Ministers, 2006; National Council of Teachers of Mathematics, 2000)。美国教育部更是将其当做提高学生数学问题解决能力最好的方法之一(Star et al., 2015)。

然而, 并不是所有的样例对比都同样有效(Gick & Paterson, 1992; Quilici & Mayer, 1996;Rittle-Johnson, Star, & Durkin, 2009; 杨凌燕, 郭建鹏, 2014)。对比的有效性主要受到多重样例变异性和学生先前知识的影响, 但是已有研究对于这些影响并未得出一致的结论。首先, 研究者还不明确多重样例之间多大程度的相似或相异才能促进学习(Renkl, Stark, Gruber, & Mandl, 1998; Rittle-Johnson& Star, 2009)。样例一般被分为表面(无关)特征和结构(相关)特征(Gick & Holyoak, 1983; Holyoak &Koh, 1987; Paas & van Merriënboer, 1994; Reed,1989; Ross, 1997)。根据 Holyoak 和 Koh (1987)的定义, 表面特征与学习目标无关, 如名称、对象、数字、表面概貌等; 结构特征与学习目标相关, 如数学法则、原理、解法等(Quilici & Mayer, 1996; Ross& Kilbane, 1997)。比如, 一个苹果是水果这个概念的一个样例。苹果的形状、大小和颜色是这个苹果的表面特征, 而可食用性则是这个苹果的结构特征。样例变异性是指多重样例之间在表面特征和结构特征上的相异或相似程度。关于多重样例表面和结构特征之间的相异度应该如何, 研究者有不同的发现。一方面有不少研究者认为具有不同表面特征的正例能够帮助学生注意到结构特征(而不是依赖于表面特征), 促进基于结构的图式建构并形成对概念(Hammer, Bar-Hillel, Hertz, Weinshall, &Hochstein, 2008; Merrill & Tennyson, 1978; Ranzijn,1991)或 者 原 理 (Paas & van Merriënboer, 1994;Quilici & Mayer, 1996; Rittle-Johnson & Star, 2009;宁宁, 喻平, 2010)较为准确的理解。如果学习表面特征类似的样例, 学生可能会把表面特征认为是相关特征, 从而影响图式建构和未来的问题解决(Quilici & Mayer, 1996; Reed, 1989)。另一方面也有研究得出了相反的结论, 认为表面类似的样例会帮助学生注意到深层的结构共性并建构图式; 高变异的样例反而会让样例的结构特征更难以被发现(Namy & Clepper, 2010; Richland, Holyoak, &Stigler, 2004; Ross & Kennedy, 1990)。还有研究发现结构特征变异的多重样例比表面特征变异更有利于学习(Curry, 2004; van Dooren, de Bock, Hessels,Janssens, & Verschaffel, 2004; 张奇, 赵弘, 2008)。

其次, 学生先前知识对样例对比学习的影响也不明确。主要存在以下几种相互矛盾的结论：(1)先前知识低的学生无法受益于样例对比, 尤其是复杂不熟悉的样例(Holmqvist, Gustavsson, & Wernberg,2007; Schwartz & Bransford, 1998); (2)先前知识高的学生应该对比学习高变异样例, 而先前知识低的学生应该对比学习低变异样例(Große & Renkl,2006, 2007; 刑强, 莫雷, 2005); (3)先前知识高的学生可以对比学习任何样例, 而先前知识低的学生只能对比学习高变异样例(Quilici & Mayer, 1996); (4)学生的先前知识与样例变异性之间不存在交互作用(Renkl et al., 1998)。可以说, 多重样例应该如何变异？应该对比样例的什么特征？适用于什么学生？等等这些问题尚未得到解决(Guo, Pang, Yang,& Ding, 2012; Rittle-Johnson et al., 2009)。

此外, 已有研究大多数是实验室研究, 很少基于真实课堂环境, 以学龄学生为对象, 探讨多重样例对比在数学学习中的作用(Rittle-Johnson & Star,2007, 2009; Star & Rittle-Johnson, 2009)。为此,Rittle-Johnson等人进行了系列课堂研究, 探讨多重样例变异性和学生先前知识在学习解一元一次方程中的作用。Rittle-Johnson和Star (2007, 2009)指出学习解方程具有两个关键特征(见表 1)：问题类型和解法, 并比较了三种样例变异类型的学习效果：(1)对比相同方程类型的不同解法; (2)对比不同方程类型的相同解法; 以及(3)依次学习每种解法,但没有进行对比。他们发现第一种样例的学习效果最好。Rittle-Johnson等人(2009)进一步探讨学生关于解法的先前知识是否会影响对比学习的有效性。结果表明, 先前知识较高的学生更能受益于对比上述第一种变异类型的多重样例, 而先前知识较低的学生更适合学习其他变异类型的样例。

在 Rittle-Johnson等人的研究中, 学生只是对比相同方程类型的不同解法或者对比不同方程类型的相同解法; 只有解法或方程的问题类型单独发生变化。由于解法和问题类型都是学习解方程的关键特征, 因此有必要进一步研究这两个特征的变化在学习解一元一次方程中的作用。Guo, Yang和Ding (2014)拓展了该研究, 他们设计了四种变异类型的样例：(1)先对比类型和解法的单独变异, 最后对比两者的同时变异; (2)只对比解法的单独变异,然后对比两者的同时变异; (3)只对比类型的单独变异, 然后对比两者的同时变异; 以及(4)先对比类型的单独变异再对比解法的单独变异, 但没有对比两者的同时变异。263名初一下学期学生通过三个阶段对比学习各自的样例。结果表明, 对于先前知识低的学生, 后三种变异类型的样例学习效果都显著好于第一种。对于先前知识高的学生, 四种变异类型的样例没有显著差别。Guo等人(2014)对研究结果的解释是, 学生在对比两个关键特征的同时变异之前, 需要足够的时间和机会去单独审辨这两个关键特征。否则当他们面对太多变异的时候就容易混淆, 无法审辨出关键特征, 从而影响学习结果。

Guo等人(2014)的解释是否正确需要进一步实证研究的验证。也就是, 如果在教学干预中给学生提供较为充分的样例学习机会以及教学支持, 确保学生在单独变异阶段能够充分审辨出每个关键特征,最后再让学生经验两个关键特征的同时变异, 这种方法是否更有利于学习？Guo等人(2014)研究的另一个不足之处在于, 被试在参加实验之前已经学过一元一次方程的常规解法。因此学生的先前知识较高,研究结果也可能会受到教师先前教学方式的影响。

针对这些不足, 本研究在Guo等人(2014)研究中四种样例变异类型的基础上, 增加了样例对比的数量与教学解释, 以确保学生能够充分审辨出每个关键特征。而且选取尚未正式学过该内容的初一上学期学生为被试, 从而更为可信地考察样例不同类型的变异在学习解一元一次方程中的作用。研究表明, 在样例学习中提供教学支持对于学习具有正面的作用(Richey & Nokes-Malach, 2013; Wittwer &Renkl, 2010)。尤其是对于初学者而言, 教学解释能够减轻样例对比时产生的认知负荷, 帮助他们注意到对比的关键特征和重要信息, 并深化样例对比所获得的知识。Wittwer和Renkl (2008)在分析了已有关于教学解释的研究后发现, 有效的教学解释需要基于学生的先前知识, 聚焦于原理或概念性信息,并且能够促进学生主动建构或应用知识。根据这些原则, 本研究在多重样例对比中设计了相应的教学解释以帮助学生对比审辨出关键特征。我们预期增加教学支持会影响Guo等人(2014)研究中四种样例变异类型的有效性。本研究的第一个问题是：先对比类型和解法的单独变异再对比两者的同时变异,这种变异类型是否比其他三种变异类型更能促进学生学习？相应的实验假设是：由于学生在对比两个关键特征的同时变异之前已经能够单独审辨出每个关键特征, 因此“先单独变异再同时变异”这种变异类型的学习效果要好于其他三种类型。本研究的第二个问题是：四种变异类型不同的教学效果是否受到学生先前知识的影响？相应的实验假设是：具有不同先前知识的学生由于审辨到不同的关键特征, 因此在四种变异类型上的学习效果也不同。

2 方法

2.1 被试

本研究的被试为厦门市一所普通中学的260名初一学生, 该中学的教学质量在全市处于中上水平。学生来自 6个班, 平均年龄 13.7岁(范围11.6～15.7岁)。被试中有5名学生没有参加前测, 4名学生没有参加后测, 因此最后的结果分析中没有纳入这9名学生的数据。学生在参加实验之前已经学过乘法分配律、化简等知识, 但还没有学过一元一次方程的解法。

2.2 实验设计

实验采取前测–干预–后测的设计。前后测用来测量学生在解一元一次方程上的程序性知识、变通性知识和概念性知识。为了探讨样例不同变异类型和学生先前知识对学习解方程的影响, 采用4(变异类型)×2(先前知识)二因素被试间实验设计。我们设计了4种变异类型的多重样例：学生通过对比不同变异的样例学习解方程, 他们(1)先对比类型和解法的单独变异再对比两者的同时变异(类型_解法_类型+解法), (2)先对比解法的单独变异再对比类型和解法的同时变异(解法_解法_类型+解法), (3)先对比类型的单独变异再对比类型和解法的同时变异(类型_类型_类型+解法), 或者(4)对比类型和解法的单独变异但没有对比两者的同时变异(类型_解法_类型/解法)。根据在前测中是否使用简便方法解方程, 把学生被分为简便方法组和无简便方法组。简便方法组的学生对解法这个关键特征的审辨要好于无简便方法组的学生。实验以学生在解一元一次方程上的程序性知识、变通性知识、概念性知识和整体表现作为因变量。

通过比较类型_解法_类型+解法与解法_解法_类型+解法两个实验条件的学习效果, 可以了解问题类型单独变异的作用; 通过比较类型_解法_类型+解法与类型_类型_类型+解法两个实验条件的学习效果, 可以了解解法单独变异的作用; 通过比较类型_解法_类型+解法与类型_解法_类型/解法两个实验条件的学习效果, 可以了解问题类型与解法同时变异的作用。

学生被随机分到四组进行学习：类型_解法_类型+解法组(n = 63)、解法_解法_解法+类型组(n =62)、类型_类型_类型+解法组(n = 63)、或类型_解法_类型/解法组(n = 63)。学习阶段包括3天3节课的时间, 学生接受教师的讲授, 学习各自的样例组合材料, 回答材料的问题并完成练习题。

2.3 实验材料

2.3.1 学习内容

本实验选取解一元一次方程为学习内容。根据Rittle-Johnson和Guo等人的研究(Guo et al., 2014;Rittle-Johnson & Star, 2009), 学习解一元一次方程有两个关键特征：问题类型和解法。如表1所示, 一元一次方程有三种问题类型(值), 每种方程都可以用两种方法(值)解答。常规的方法是先去括号再求解, 这是最常见的解方程的方法。简便的方法是把诸如(x+3)的式子看成是一个复合变量进行运算再求解。与常规方法相比, 简便方法由于所用的步骤和运算更少, 因此更为有效和容易。

Rittle-Johnson等人(2009)发现, 只有 20%的初一和初二年级学生能够正确使用常规方法解方程,4%尝试过使用简便方法, 41%的学生在前测中从未使用代数的方法解方程。即使教师教过, 也只有20%的题目是使用简便方法解答的。为了完全掌握解方程, 学生需要同时审辨问题类型和解法这两个关键特征。也就是他们必须理解有三种类型的方程,每种方程都可以使用两种方法进行解答。

表1 解方程的两个关键特征和值

2.3.2 学习材料

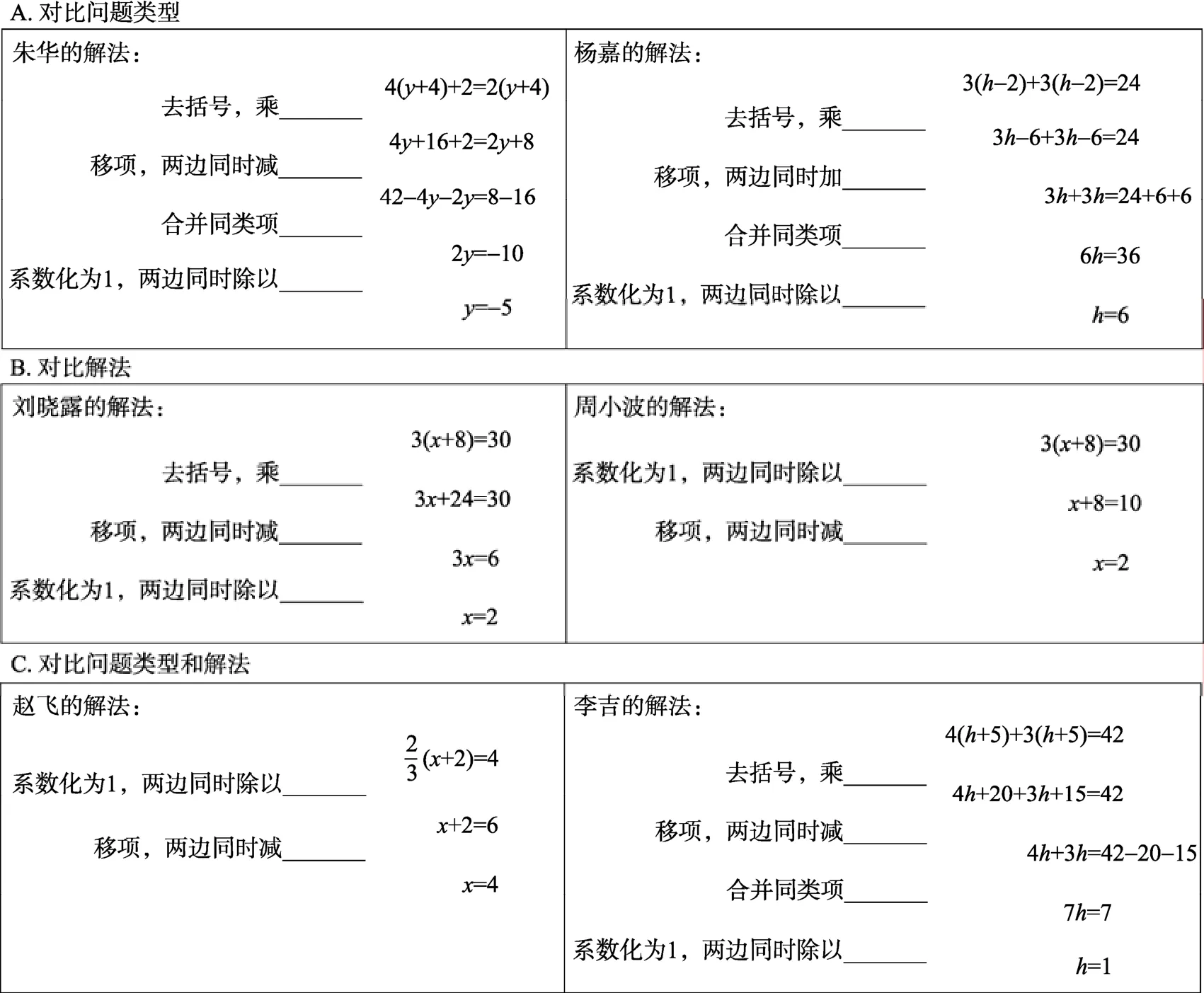
图1 三种变异类型的对比

本实验设计了4种不同类型的样例组：对比类型、对比解法、对比类型和解法、对比类型或解法。这四组之间的主要区别在于样例之间的配对。如图1和表 2所示, 在对比类型组中, 每对样例包含的两个方程问题类型不同, 但是解法相同; 问题类型这个关键特征发生变化而解法这个关键特征保持不变。在对比解法组中, 每对样例包括的两个方程问题类型相同, 但是解法不同(常规和简便); 解法这个关键特征发生变化, 而类型这个关键特征保持不变。在对比类型和解法组中, 每对样例包括的两个方程问题类型不同、解法也不同; 类型和解法这两个关键特征同时发生变化。在对比类型或解法组中, 有 3对方程配对(6个样例)与对比类型组相似,具有相同解法但不同类型, 另外3对方程配对(6个样例)与对比解法组相似, 具有相同类型但不同解法; 类型和解法这两个关键特征都是单独变化而非同时变化。因此, 图1只举例说明前三种变异类型。

除了样例的配对方式不同之外, 每组样例都尽可能保持相似。每种样例组都包括12个样例(3种类型的方程, 每种 4个样例)。一半使用常规解法,一半样例使用简便解法。

实验的四种条件由不同的样例组构成(见表3)。实验条件一包括一个对比类型组, 一个对比解法组,以及一个对比类型和解法组, 简称类型_解法_类型+解法; 实验条件二包括两个对比解法组以及一个对比类型和解法组, 简称解法_解法_类型+解法;实验条件三包括两个对比类型组以及一个对比类型和解法组, 简称类型_类型_类型+解法; 实验条件四包括一个对比类型组, 一个对比解法组, 以及一个对比类型或解法组, 简称类型_解法_类型/解法。

表2 四种类型样例组的比较

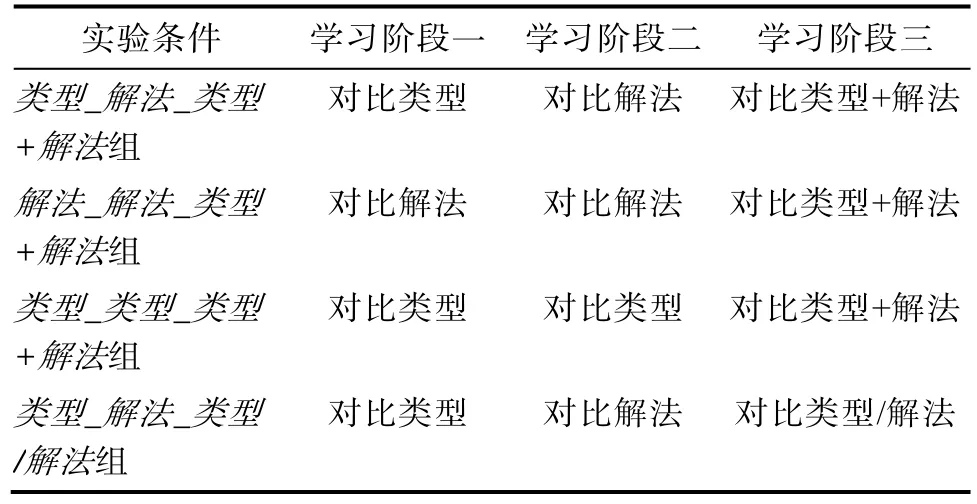
表3 四种实验条件的比较

学生通过三个阶段学习各自的材料。因此, 类型_解法_类型+解法组的学生首先对比不同类型但相同解法的方程, 然后对比相同类型但不同解法的方程, 最后对比不同类型和不同解法的方程; 他们首先对比两个关键特征的单独变异(类型和解法),然后对比两个特征的同时变异。解法_解法_类型+解法组的学生在前两个学习阶段对比相同类型但不同解法的方程, 最后对比不同类型和不同解法的方程; 他们首先对比解法这个关键特征的单独变异,然后对比两个特征的同时变异, 他们没有对比类型这个关键特征的单独变异。类型_类型_类型+解法组的学生在前两个学习阶段对比不同类型但相同解法的方程, 最后对比不同类型和不同解法的方程;他们首先对比类型这个关键特征的单独变异, 然后对比两个特征的同时变异, 他们没有对比解法这个关键特征的单独变异。类型_解法_类型/解法组的学生在前两个学习阶段对比类型和解法这两个关键特征的单独变异; 在第三个学习阶段, 他们没有对比两个关键特征的同时变异, 而是对比与前两个阶段类似的方程(对比类型或对比解法)。

与Guo等人(2014)的研究不同, 本研究中的四组学生在第三个阶段对比学习了 12个样例, 样例数量为Guo等人(2014)研究的两倍, 从而增加了前三组学生对比类型和解法同时变异的机会以及第四组学生对比类型和解法单独变异的机会。所有学生在每个学习阶段都对比学习 12个样例, 三个阶段共学习 36个样例。除了样例的配对方式不同之外, 实验条件之间的其他方面尽量保持一致。在第三个学习阶段的最后, 学生被要求使用两种不同的方法解答四道练习题。最后一页提供答案让学生检查自己的理解是否正确。

2.3.3 测试材料

前后测材料是纸笔测验的形式, 用来测试学生在解方程上的程序性知识(procedural knowledge)、变通性知识(flexibility knowledge)和概念性知识(conceptual knowledge)。这三类知识代表了三种重要的数学能力(Hiebert, 1986; Kilpatrick, Swafford,& Findell, 2001; Rittle-Johnson & Star, 2009;Verschaffel, Luwel, Torbeyns, & van Dooren, 2009)。程序性知识体现为通过多个步骤解决问题的能力;变通性知识体现为使用不同的方法解决问题以及识别、解释不同方法优劣的能力; 概念性知识是指对数学知识的整体性和功能性的掌握, 体现为识别和解释相关概念的能力。这三类知识也分别对应了Alexander对领域知识的三种分类(Alexander,Schallert, & Hare, 1991)。其中, 概念性知识是关于“是什么” (knowing what)的陈述性知识, 程序性知识是关于“如何做” (knowing how)的过程性知识,变通性知识是关于“何时何地做” (knowing when and where)的条件性知识。

前后测题目相同, 共19道题目, 样题如表4所示。为了把研究结果与 Rittle-Johnson等人(Rittle-Johnson & Star, 2007, 2009; Rittle-Johnson et al.,2009)和Guo等人(2014)的研究进行对比, 我们采用了Guo等人(2014)的测试材料。程序性知识包括7道题目, 测试学生解决熟悉、近迁移和远迁移问题的能力。熟悉的问题与干预材料中的样例具有相同的问题类型。近迁移的问题在括号里面增加了变量以及新的运算符号。远迁移的问题要求使用方程知识来解答实际问题。变通性知识通过三种方式测量：(1)用两种方法解答某个方程(2题), (2)判断某个问题的第一步解法是否合适(2题), (3)判断非常规解法的正确性与有效性(2题)。概念性知识测量学生关于等式、同类项和复合变量的言语及非言语性知识, 共6道题目。

2.4 实验程序

实验包括5天5节课的时间。第1天为前测阶段, 测试学生对解一元一次方程的先前知识。组织被试安静地坐在自己的座位上, 实验期间被试不许交流, 有问题举手提问。指导语是：“请同学们做一套关于一元一次方程解法的卷子。大家还没有学过,所以不会做也很正常, 只是想了解大家学习之前掌握到了什么程度。大家只要尽力答题就可以了, 请大家把自己所想的都写下来。”被试拿到测试题后即可作答, 35 min答题时间结束后交卷。最后教师用 15 min讲解四道整式的化简和去括号, 实验中的教师都是本研究的助理。

前测结束一周之后, 学生被随机分到四组进行学习, 学习阶段共包括3天3节课时间。第2天的学习阶段包括45 min, 教师先用15 min简单介绍实验、带领学生一起解答3道整式和方程并解释解题步骤。指导语是：“同学们, 今天我们要来学习一元一次方程的解法。由于整式的内容我们还没有学习,所以现在我们先用几分钟的时间来学习一些基本的知识, 这些对等下要学习的一元一次方程的解法是很重要的。”然后学生用剩下的30 min学习材料,时间还剩10min结束的时候, 教师会提醒学生。学习结束后上交材料。第3天和第4天的学习遵循与第2天同样的方式。在第4天的最后, 教师用8 min简单总结并解释：(1)解方程有一种以上的方法, (2)只要方程的两边保持相等, 任何解法都可以, (3)有些解法比其他解法更容易、更好。

不同于Guo等人(2014)的研究, 本研究在3天的学习阶段中(第 2～4天)为学生提供了更多的教学解释。在学生对比学习样例之前, 教师通过整式运算向学生解释如何去括号、移项、合并同类项、把系数化为 1等基本知识, 并告诉学生解方程最后要得出“字母 = 常数”的形式, 这个字母可能是 x、y或其他字母。教师依次介绍三种类型的方程以及含有分数的方程。教师提醒学生解方程可能不止有一种方法, 要想想用什么方法比较简单且不容易犯错, 解题过程要保持等式两边始终相等。在教学解释中, 教师基于学生先前的学习经验, 介绍相关的原理和概念性知识,并注意引导学生主动分析、总结归纳、建构知识。

第5天为后测阶段, 时间为45 min。在前后测中, 教师都会简单介绍测试题, 向学生解释需要完成的任务。教师告诉学生答题时要解释他们的答案,并尽可能把想到的都写下来。学生的答案不会让他们的老师和学校看到。测试结束前 10 min提醒学生。为了保证实验的可信性, 教师严格按照规定进行介绍和监考, 作者只是在必要的时候为教师提供指导和帮助, 并进行观察。

2.5 评分标准

如表4所示, 程序性知识的7道题目根据答案正确与否进行评分。另外, 根据前测中学生在程序性知识和变通性知识的“一题两解”中是否使用简便方法, 把学生分成简便方法组和无简便方法组。变通性知识和概念性知识的评分标准见表4。评分由两名独立的评分者分别完成, 两人评分不同的题目则通过讨论达成一致。

2.6 数据分析

为了探讨实验条件和先前知识之间的交互效应, 我们对学生的整体表现以及三类测试结果都进行了二因素协方差分析(ANCOVA)。把学生在前测中是否使用简便方法和实验条件作为组间变量, 学生的前测分数和数学能力(基于学生的期中数学考试分数)作为协变量控制先前知识的差异。如果交互效应显著, 则进行简单效应分析来进一步探讨实验条件的影响。首先对比类型_解法_类型+解法组和解法_解法_类型+解法组, 然后对比类型_解法_类型+解法组和类型_类型_类型+解法组, 最后对比类型_解法_类型+解法组和类型_解法_类型/解法组。

3 结果

3.1 先前知识

表5总结了学生在全部测试题目上的前后测表现。可以看出, 学生在解一元一次方程上具有一定的先前知识。有些学生甚至在某些题目上得到满分。然而, 大多数学生的理解都比较片面。只有不到1%的程序性知识题目使用简便方法解答。47.8%的学生在前测中至少使用一次简便方法解题, 并被划分为简便方法组; 其他学生在前测中从未使用简便方法, 被划分为无简便方法组。无简便方法组的学生在变通性知识题目上平均得 5.74分(满分 24分), 在概念性知识题目上平均得 1.74分(满分 7分)。表明他们还没有审辨出解法这个关键特征, 无法把(x+1)之类的表达式看成是一个复合变量, 并使用简便方法来解题。即使是简便方法组的学生,虽然他们尝试使用复合变量的简便方法解方程, 但他们的先前知识也不高; 在变通性知识题目上平均得10.03分, 在概念性知识题目上平均得2.85分。

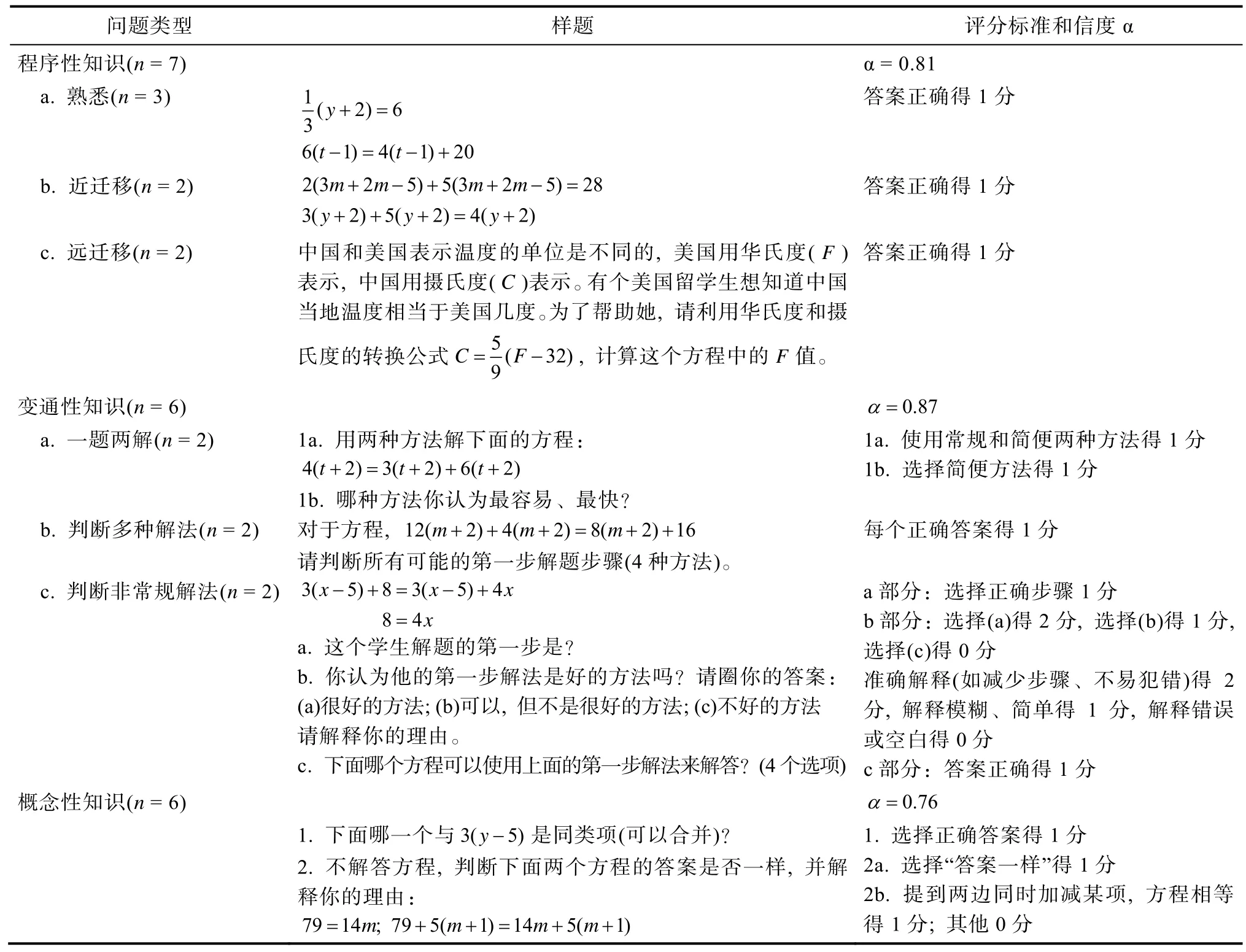
表4 程序性知识、变通性知识和概念性知识的前后测样题与评分标准

程序性知识与变通性知识和概念性知识显著相关, r (251) = 0.44以及r (251) = 0.36, ps < 0.001;变通性知识与概念性知识显著相关, r (251) = 0.64,p < 0.001。学生在全部测试题中的后测分数都显著高于前测分数(ps < 0.01), 表明所有学生通过学习在程序性知识、变通性知识和概念性知识上都有了明显的进步。前测使用简便方法的学生各类前测分数都显著高于前测没有使用简便方法的学生(ps <0.001)。不同实验组在前测程序性知识、变通性知识和概念性知识上都不存在显著差异(ps > 0.05)。

3.2 实验条件(类型_解法_类型+解法组与解法_解法_类型+解法组)与先前知识的影响

3.2.1 整体表现

如图 2a所示, 实验条件(类型_解法_类型+解法组与解法_解法_类型+解法组)和前测是否使用简便方法之间存在显著的交互作用, F(1, 117) = 8.56,MSE = 32.42, p < 0.005, η= 0.07。实验条件和前测是否使用简便方法的主效应都不显著(ps > 0.05)。我们进一步进行简单效应分析发现, 对于前测没有使用简便方法的学生, 类型_解法_类型+解法组显著好于解法_解法_类型+解法组, F(1, 117) = 3.98,MSE = 32.42, p < 0.05, η= 0.03。相反对于前测使用简便方法的学生, 解法_解法_类型+解法组则显著好于类型_解法_类型+解法组, F(1, 117) = 4.61,MSE = 32.42, p < 0.05, η= 0.04。

3.2.2 程序性知识

如图 2b所示, 实验条件和前测是否使用简便方法之间的交互效应不显著(p = 0.18)。实验条件和前测是否使用简便方法的主效应也都不显著(ps >0.05)。这表明两种实验条件对学习程序性知识的影响并没有差别, 也没有受到先前知识的作用。

3.2.3 变通性知识

如图 2c所示, 实验条件和前测是否使用简便方法之间存在着显著的交互作用, F(1, 117) =6.53, MSE = 18.58, p < 0.05, η= 0.05。实验条件和前测是否使用简便方法的主效应都不显著(ps >0.05)。简单效应分析显示, 对于前测没有使用简便方法的学生, 两种实验条件的效果没有显著差别(p =0.13)。但是对于前测使用简便方法的学生, 解法_解法_类型+解法组要显著好于类型_解法_类型+解法组, F(1, 117) = 4.26, MSE = 18.58, p < 0.05, η= 0.04。

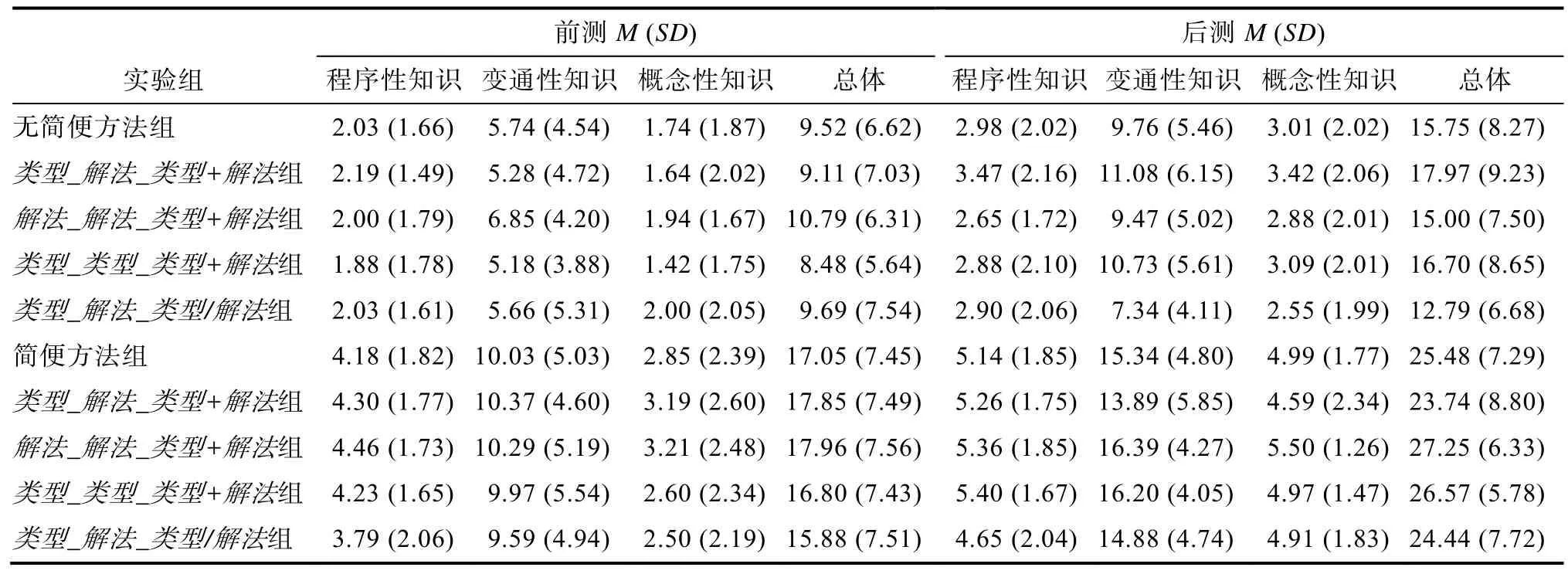
表5 学生在各类测试上的前后测分数(实验条件×前测是否使用简便方法)

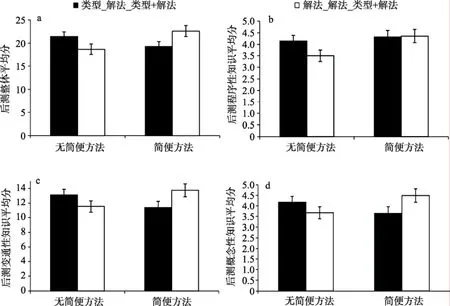
图 2 实验条件与前测是否使用简便方法在后测整体表现(a)、程序性知识(b)、变通性知识(c)和概念性知识(d)上的交互。模型的协变量包括前测程序性知识、变通性知识、概念性知识和数学能力。误差线为标准误。

3.2.4 概念性知识

最后是学生的概念性知识。如图2d所示, 实验条件和前测是否使用简便方法之间存在着显著的交互作用, F(1, 117) = 5.86, MSE = 2.40, p < 0.05, η= 0.05。实验条件和前测是否使用简便方法的主效应都不显著(ps > 0.05)。简单效应分析表明, 对于前测没有使用简便方法的学生, 两种实验条件的效果不存在显著差别(p = 0.18)。但是对于前测使用简便方法的学生, 解法_解法_类型+解法组要显著好于类型_解法_类型+解法组, F(1, 117) = 4.18, MSE =2.40, p < 0.05, η= 0.03。

3.3 实验条件(类型_解法_类型+解法组与类型_类型_类型+解法组)与先前知识的影响

如图3所示, 实验条件(类型_解法_类型+解法组与类型_类型_类型+解法组)和前测是否使用简便方法的交互效应在各类测试结果上(包括学生的整体表现、程序性知识、变通性知识和概念性知识)都不显著, 实验条件和前测是否使用简便方法的主效应也都不显著(ps > 0.05)。这表明两种实验条件对学习解一元一次方程的影响并没有差别, 而且也没有受到先前知识的作用。

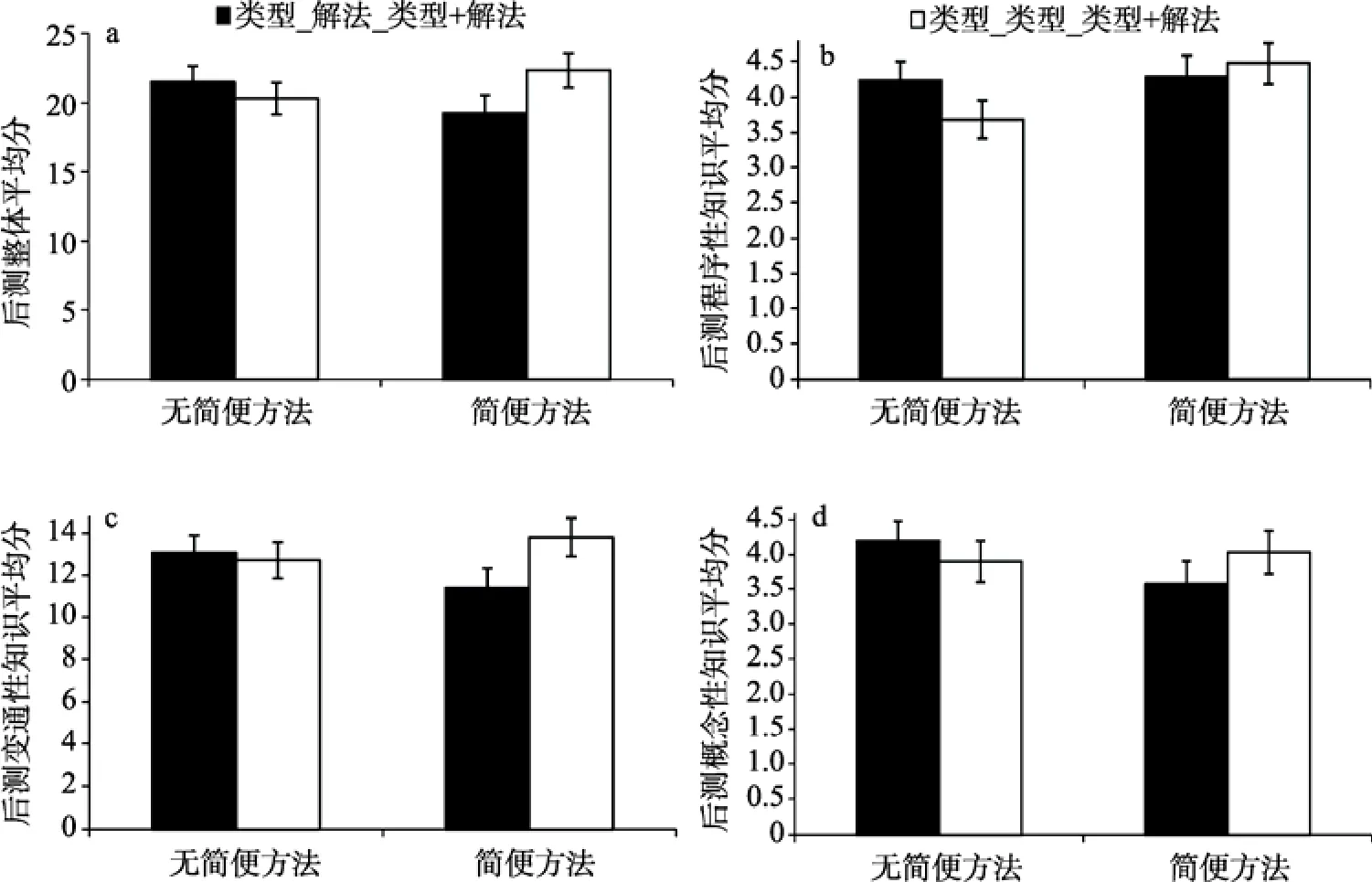
图 3 实验条件与前测是否使用简便方法在后测整体表现(a)、程序性知识(b)、变通性知识(c)和概念性知识(d)上的交互。模型的协变量包括前测程序性知识、变通性知识、概念性知识和数学能力。误差线为标准误。

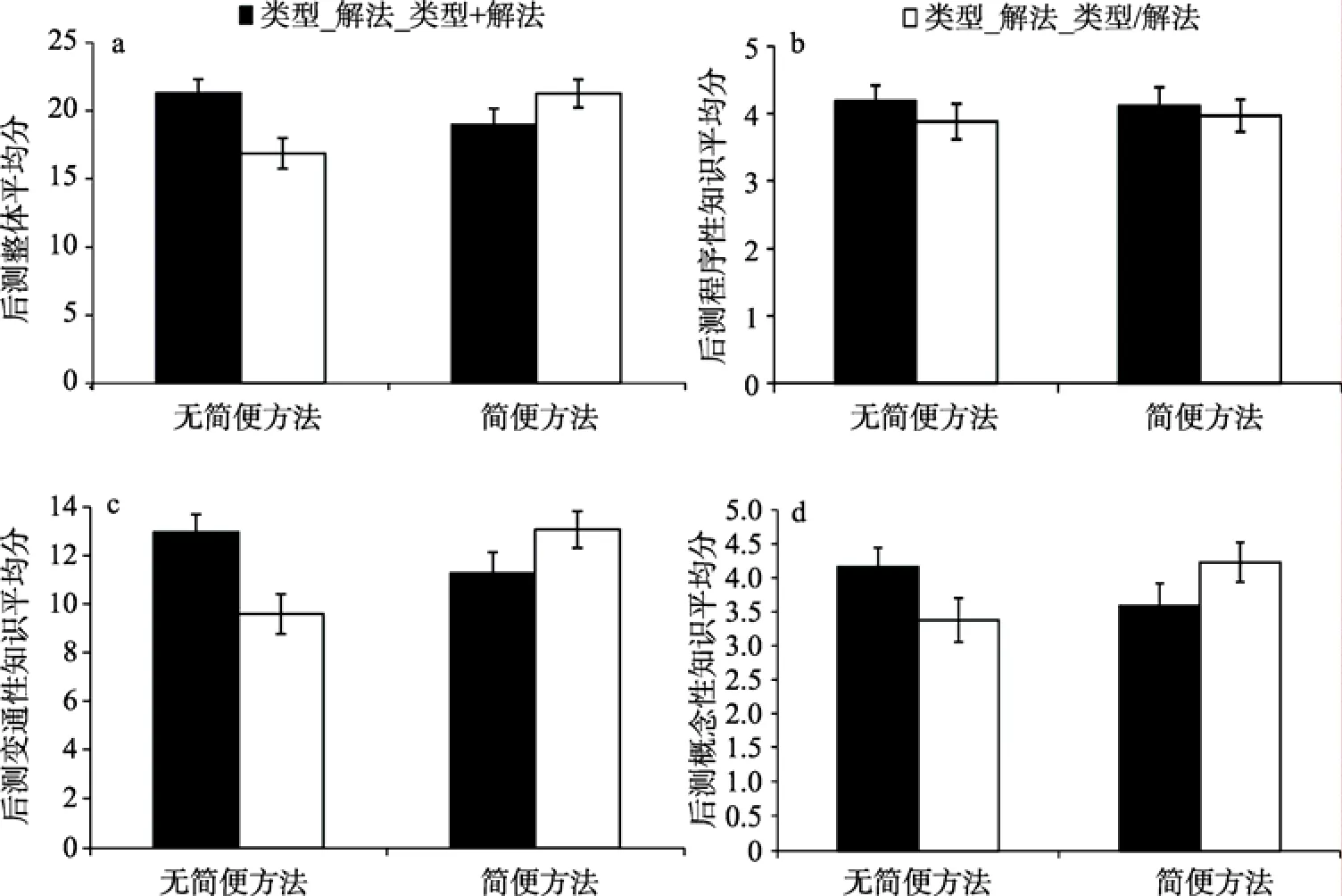
图 4 实验条件与前测是否使用简便方法在后测整体表现(a)、程序性知识(b)、变通性知识(c)和概念性知识(d)上的交互。模型的协变量包括前测程序性知识、变通性知识、概念性知识和数学能力。误差线为标准误。

3.4 实验条件(类型_解法_类型+解法组与类型_解法_类型/解法组)与先前知识的影响

3.4.1 整体表现

如图 4a所示, 实验条件(类型_解法_类型+解法组与类型_解法_类型/解法组)和前测是否使用简便方法之间存在着显著的交互作用, F(1, 118) =10.53, MSE = 32.96, p < 0.005, η= 0.08。实验条件和前测是否使用简便方法的主效应都不显著(ps >0.05)。简单效应分析发现, 对于前测没有使用简便方法的学生, 类型_解法_类型+解法组要显著好于类型_解法_类型/解法组, F(1, 118) = 9.52, MSE = 32.96,p < 0.005, η= 0.02。对于前测使用简便方法的学生,两种实验条件没有显著的差别(p = 0.13)。

3.4.2 程序性知识

如图 4b所示, 实验条件和前测是否使用简便方法之间交互效应不显著(p = 0.75)。实验条件和前测是否使用简便方法的主效应也都不显著(ps >0.05)。这表明两种实验条件对学习程序性知识的影响并没有差别, 也没有受到先前知识的作用。

3.4.3 变通性知识

如图 4c所示, 实验条件和前测是否使用简便方法之间存在着显著的交互作用, F(1, 118) = 11.58,MSE = 17.58, p = 0.001, η= 0.09。实验条件和前测是否使用简便方法的主效应都不显著(ps > 0.05)。简单效应分析显示, 对于前测没有使用简便方法的学生, 类型_解法_类型+解法组要显著好于类型_解法_类型/解法组, F(1, 118) = 10.21, MSE = 17.58,p < 0.01, η= 0.08。对于前测使用简便方法的学生,两种实验条件没有显著的差别(p = 0.10)。

3.4.4 概念性知识

如图 4d所示, 实验条件和前测是否使用简便方法之间存在着显著的交互作用，F(1, 118) = 5.88,MSE = 2.65, p < 0.05, η= 0.05。实验条件和前测是否使用简便方法的主效应都不显著(ps > 0.05)。简单效应分析发现, 对于前测没有使用简便方法的学生, 类型_解法_类型+解法组的学习效果好于类型_解法_类型/解法组, 差异达到边际性显著, F(1,118) = 3.65, MSE = 2.65, p = 0.059, η= 0.03。对于前测使用简便方法的学生, 两种实验条件之间不存在显著差异(p = 0.13)。

4 讨论

4.1 主要研究结果

与本研究的假设一致, 实验结果表明多重样例不同的变异类型对学生学习解一元一次方程的作用受到学生先前知识的影响。尤其是在增加教学支持的情况下, 样例变异类型的有效性相比先前研究发生了变化。总的来说, 有以下几点发现。

第一, 对于前测没有使用简便方法的学生来说,类型_解法_类型+解法要好于其他方法, 尤其是其在促进变通性知识和概念性知识的发展上要显著好于类型_解法_类型/解法组。表明对问题类型和解法这两个关键特征先单独变异再同时变异能够促进这些学生更好地审辨这两个特征, 获得更多的变通性知识和概念性知识, 在方程解法的选择上更具灵活性, 对方程思想的理解更为深入。如果样例设计中没有同时变化这两个特征, 则会影响学生对于方程解法的运用及理解。“先单独再同时”变异类型的有效性与Pang和Marton (2005)、Ki (2007)以及Guo和Pang (2011)等研究的结论一致。单独变异能够帮助学生审辨出每个关键特征, 不会被太多变异所混淆, 是同时变异的基础; 同时变异则会帮助学生形成对知识的全面理解, 是单独变异的发展和深化。

第二, 对于前测使用简便方法的学生来说, 解法_解法_类型+解法在促进变通性知识和概念性知识的发展上要显著好于类型_解法_类型+解法组。这可能是因为一方面这些学生已经较好地掌握了问题类型这个特征, 另一方面虽然他们在前测中尝试使用过简便方法解题, 但是较低的前测分数(见表5)显示他们对简便方法也并不熟悉。解法_解法_类型+解法组由于提供了较多的机会让学生对比解法的单独变异, 因此能够帮助他们更好地审辨解法这个关键特征。另外, Rittle-Johnson等人(2009)指出, 学生只有在熟悉常规解法的前提下才能受益于对比解法的多重样例, 通过对比熟悉(常规解法)和不熟悉(简便解法)的两种解法来认识解法这个特征。前测使用简便方法的学生对常规解法的掌握要显著好于前测没有使用简便方法的学生(p < 0.05),因此他们也就更能受益于对比解法的样例。

第三, 与变通性知识和概念性知识不同, 实验条件与先前知识在程序性知识的学习上并不存在显著的交互效应和主效应。表明不同的实验条件在促进学生学习程序性知识上效果类似。Rittle-Johnson和Star (2009)也发现, 对比问题类型和对比解法在提高学生的程序性知识上效果没有显著差别。这可能是因为程序性知识体现为学生解方程的正确率。学生既可以使用常规方法也可以使用简便方法答题。一般的样例对比至少能够帮助学生掌握并使用常规方法解方程, 因此不同实验条件的效果没有显著差别。不同实验条件的差别主要体现在多种解法尤其是简便解法的使用和理解, 即解方程的变通性知识和概念性知识。

4.2 对比相关研究结果

本研究还发现, 在增加样例对比数量和教学解释的情况下, 样例变异类型的有效性及其与先前知识的交互作用表现出与Guo等人(2014)研究不同的特点：对于前测没有使用简便方法的学生, 类型_解法_类型+解法比其他方法更能促进学生的变通性知识; 而对于前测使用简便方法的学生, 类型_解法_类型+解法的学习效果则相反。Guo等人(2014)发现, 对于前测没有使用简便方法的学生, 类型_解法_类型+解法在促进变通性知识学习上效果最差; 而对于前测使用简便方法的学生, 不同实验条件的学习效果则类似。

上述不一致的结论可以从两个研究两点不同的设计进行解释。首先是两个研究在教学支持上的不同。Guo等人(2014)指出, 类型_解法_类型+解法的前两个学习阶段可能没有提供足够的机会让学生单独审辨类型和解法这两个关键特征。因此在第三个阶段同时变化两个特征时, 无简便方法组的学生会被太多变异混淆而无法审辨出关键特征, 导致类型_解法_类型+解法的学习效果不如其他方法。为了解决这个问题, 本研究在学生学习阶段增加了样例对比的数量以及教师的教学解释, 帮助学生在对比样例之前熟悉去括号、移项、合并同类项、化简等相关知识, 引导学生主动建构解方程的知识。较为充分的教学支持尤其能够帮助先前知识较低的学生在对比学习类型_解法_类型+解法时, 能够首先单独审辨出问题类型和解法这两个关键特征,并最后受益于第三个阶段的同时变异。这表明适当的教学解释对于发挥样例对比的有效性是必要的,能够降低对比时产生的认知负荷, 帮助学生把有限的认知资源集中于对比样例的关键特征上。

其次是两个研究在被试先前学习经验上的不同。在Guo等人(2014)的研究中, 学生参加实验之前虽然还没有学过一元一次方程的简便解法, 但已经在学校学过常规解法。参与本研究的学生则还未学过方程的常规解法和简便解法。这就会导致一方面, Guo等人(2014)的研究结果可能会受到教师先前教学方法的影响, 而本研究的结果则较能反映不同实验条件的学习效果。另一方面, 两个研究被试在解方程上不同的先前知识也会影响实验条件的效果。数据分析结果显示, 本研究被试对于常规解法和简便解法的掌握和熟悉程度都低于 Guo等人(2014)研究的被试。虽然学生也根据前测表现被分为无简便方法组和简便方法组, 但两组学生的先前知识与Guo等人(2014)的两组学生不同。比如本研究中无简便方法组的学生前测变通性知识平均得分5.74分, 简便方法组的学生前测变通性知识平均得分 10.03分。而在 Guo等人(2014)的研究中, 无简便方法组的学生前测变通性知识平均得分 8.14分, 简便方法组的学生前测变通性知识平均得分13.24分。在概念性知识上, Guo等人(2014)研究中无简便方法组的学生甚至高于本研究简便方法组的学生。具有不同先前知识的被试对于关键特征的审辨不同, 因此对样例不同变异类型的学习效果也就不同。未来研究应进一步探讨教学解释与样例变异类型在促进不同先前知识学生学习上的作用。

4.3 如何有效进行多重样例对比？

虽然多重样例研究表明对比在学习中的重要作用, 但是关于“怎么对比”的问题却没有得出一致的结论(Guo et al., 2012)。本研究考察了单独变异和同时变异在对比学习中的作用。结果表明, 在多重样例设计中, 需要创造机会让学生首先单独对比学习的关键特征, 最后再让学生同时对比全部关键特征。Schwartz等人(Bransford & Schwartz, 1999;Schwartz & Bransford, 1998; Schwartz & Martin,2004)指出, 多重样例对比学习的有效性在于能够帮助学生发展出辨别性知识。通过样例对比学生能够注意到区别样例的特定特征和属性并形成辨别性知识结构, 这成为了他们日后学习的基础。变易理论(variation theory) (详见Marton & Booth, 1997;Pang & Marton, 2005)进一步指出, 学习是一种审辨的过程, 审辨就需要经验变异。当事物某个方面的特征变化而其他特征保持不变时, 这个变化的特征就会被审辨出来。单独变异是指只有一个关键特征的值变化, 其他关键特征保持不变; 同时变异是指多个关键特征的值同时发生变化。单独变异和同时变异为系统设计多重样例的变异性提供了一种方法。在确定了学生学习的关键特征之后, 首先单独变异每个关键特征, 让学生通过对比分别审辨出每个关键特征。最后再同时变异全部关键特征, 让学生通过体验关键特征的同时变化来达到全面的审辨学习。如果学生没有单独审辨出每个关键特征就直接对比全部关键特征的变化, 他们就容易迷失于太多的变异中; 相反如果学生只是单独对比每个关键特征的变异而没有经验全部关键特征的同时变化, 他们对所学知识的理解就不够深刻和全面。

单独变异和同时变异的作用也可以从认知负荷理论得到解释。根据认知负荷理论, 高变异的多重样例由于存在较多的要素关系从而产生比低变异样例更高的内在认知负荷(intrinsic cognitive load),学生在对比这些高变异样例的时候很容易出现认知超负荷从而无法有效完成对比(Sweller, 2010)。如果学生在对比高变异样例之前首先通过单独对比分别审辨出每个关键特征, 那么当他们对比全部关键特征的同时变异时, 工作记忆就不会负荷过重从而影响学习。先单独变异再同时变异的方法一方面能够降低学生样例学习时的外在认知负荷(extraneous cognitive load), 帮助他们使用较少的认知资源就能够审辨出学习的关键特征; 另一方面也能够提高样例学习时的相关认知负荷(germane cognitive load),促进学生积极主动地进行对比和图式构建。Sweller(2010)指出, 在保证认知总负荷不超过学生工作记忆容量的前提下, 应该尽可能地增加内在认知负荷和样例的变异性; 但是如果学生的工作记忆出现超负荷就应该降低样例的变异性, 减少内在认知负荷。先单独变异再同时变异的方法能够在增加内在认知负荷的同时把学生的工作记忆负荷控制在合理的范围, 从而提高了对比的有效性。此外, 本研究在学生对比多重样例中适当增加了相应的教学解释,帮助学生注意并审辨样例的关键特征, 思考、理解样例之间的异同及其体现的原理, 在降低学习外在认知负荷的同时, 提高了相关的认知负荷。

特别是对于先前知识较低的学生来说, 在对比关键特征同时变异之前首先单独审辨出每个关键特征, 并且辅以一定的教学解释, 能够有效地降低他们对比样例时的认知负荷, 减轻工作记忆的负担,从而通过多重样例对比完成图式的建构。如果多重样例对比超出学生工作记忆的容量, 就会影响对比的有效性。相反, 对于先前知识较高的学生而言,他们比低先前知识的学生审辨出更多的关键特征,具备更多的认知资源。对于低先前知识学生超负荷的样例对比材料和设计方法对于高先前知识的学生反而可能是合适的, 不会超出他们的工作记忆容量; 他们能够集中认知资源对比审辨学习的关键特征。而对于低先前知识学生有效的样例对比对于高先前知识的学生则可能是无效的、冗余的, 甚至是有害的, 迫使他们对比已经审辨出来的关键特征,加重了外在认知负荷并减少了相关认知负荷, 从而产生教学效果的逆反, 出现专长反转效应(expertise reverse effect) (Kalyuga & Renkl, 2010)。

4.4 本研究的教学实践价值及启示

本研究的结果为教师在教学中设计多重样例帮助学生学习提供了指导。虽然在教学中使用多重样例进行对比是常见的教学策略, 但是大多数教师在样例对比教学的使用上都存在着问题, 往往只能从自身主观的教学经验出发设计样例, 无法发挥出样例对比教学的最佳效果(Chazan & Ball, 1999; Richland et al., 2004; Richland, Zur, & Holyoak, 2007)。

根据本研究结果, 教师教学时首先要确定学生学习的关键特征。关键特征是指那些学生还没有掌握的、对他们理解重要的特征。教师可以使用前测、访谈、备课交流、文献综述等方法来了解学生的先前知识并确定他们学习的关键特征。虽然要找到学生的关键特征并不容易, 但是有效教学必须基于这些关键特征来进行设计。

一方面, 教学如果没有提供充分的机会让学生对比学习关键特征, 低先前知识的学生可能会出现学习困难。在本研究中, 解法_解法_类型+解法、类型_类型_类型+解法、类型_解法_类型/解法三种方法由于缺少关键特征的单独变异或同时变异, 导致学生的学习结果不如类型_解法_类型+解法组。另一方面, 教学如果关注了非关键特征就会减少高先前知识学生对比学习的机会, 从而导致低效的教学。比如高先前知识的学生由于已经掌握了类型和解法这两个关键特征, 那么基于这两个特征设计的教学方法就无法取得很好的效果。

总而言之, 如果没有考虑个体学生在关键特征上的差异, 教学的有效性就难以实现。这与传统教育心理学关于个人特质与实验条件的交互作用研究(aptitude-treatment interaction, ATI)以及近期关于专长反转效应的研究相一致。根据这些研究, 教学方法与学生的个人特质之间存在着交互效应, 对一部分学生有效的教学方法对另一部分学生可能是无效的, 甚至反转为有害的(Kalyuga, 2007; Kalyuga& Renkl, 2010; Tobias, 1989)。然而这些研究并没有明确说明学生的何种特质会显著影响教学成效。本研究结果表明, 对比作为一种重要的教学方法, 其有效性会受到学生特质的影响; 而学生的先前知识尤其是他们对关键特征的审辨是影响教学成效的一种重要的个人特质。

确定学生学习的关键特征之后, 为了帮助学生审辨这些关键特征, 应该对这些特征首先单独变异,然后再同时变异。“先单独再同时”的变异类型能够系统控制多重样例的变异性, 帮助学生一方面能够循序渐进地识别、掌握每个关键特征, 另一方面能够形成对知识的全面理解。本研究中的类型_解法_类型+解法组就是首先单独变异类型和解法这两个关键特征, 然后再同时变异这两个特征来帮助学生学习方程的解法。缺少单独变异会使得同时变异超出学生的理解范畴; 而缺少同时变异则会使得单独变异停留在较浅的水平, 无法达到全面理解。

4.5 本研究的不足与未来研究展望

虽然本研究定义了学习解方程的两个关键特征：问题类型和解法。但是在前后测设计中我们主要考察学生对于解法这个关键特征的掌握和熟悉程度, 并没有针对问题类型专门设计题目。因此一方面我们无法了解学生关于方程问题类型的掌握程度, 另一方面也会导致对比解法的样例组更有利于学生的后测表现。未来研究应该进一步设计相应的题目考察学生关于问题类型的掌握程度, 以更好地探讨对比类型样例组的学习效果。此外, 本研究虽然探讨了4种变异类型的有效性, 但是还存在其他变异类型需要加以研究。比如只比较解法的单独变异、或者只比较类型的单独变异。对多种变异类型的有效性进行探讨能够帮助我们进一步了解应该如何设计多重样例变异性。

本研究在前后测中采用相同的题目以了解学生的进步情况, 为了控制可能出现的练习效应, 本研究的后测安排在前测完成后 11天才进行, 所有学生都接受同样的前后测, 并且在结果分析中把学生的前测分数作为协变量以平衡不同实验组先前知识的差异。未来研究可以探讨使用不同的前后测题目, 并加入间隔时间更长的延迟后测, 以消除练习效应产生的实验误差对研究结论的影响。本研究中学生虽然通过学习都获得了明显的进步, 但是学生的后测平均分并不是很高, 表明学生并没有很好地掌握方程的解法。这可能是因为学生主要通过样例对比自学, 导致本研究中各种变异类型的教学效果差别不是十分明显。我们认为, 在样例对比中增加教学支持能够进一步体现各种变异类型对学习的不同影响。但是由于教学支持并不是本研究实验的自变量, 因此本文没有进一步讨论教学支持对学习解方程的影响, 及其与变异类型和先前知识之间可能存在的交互作用。未来研究可以把教学支持(如教学解释)作为自变量深入探讨教学支持的作用。

5 结论

(1)设计多重样例变异性时需要首先单独变异每个关键特征, 最后再同时变异全部关键特征。确保学生在单独审辨出每个关键特征的基础上经验全部关键特征的同时变化。

(2)设计多重样例时, 需要提供充分的教学支持来帮助学生对比审辨学习的关键特征。

(3)具有不同先前知识的学生学习的关键特征不同, 多重样例的变异性要依据学生不同的关键特征进行设计。

Alexander, P. A., Schallert, D. L., & Hare, V. C. (1991).Coming to terms: How researchers in learning and literacy talk about knowledge. Review of Educational Research, 61,315–343.

Alfieri, L., Nokes-Malach, T. J., & Schunn, C. D. (2013).Learning through case comparisons: A meta-analytic review. Educational Psychologist, 48, 87–113.

Atkinson, R. K., Derry, S. J., Renkl, A., & Wortham, D.(2000). Learning from examples: Instructional principles from the worked examples research. Review of Educational Research, 70, 181–214.

Australian Education Ministers. (2006). Statements of learning for mathematics. Carlton South Vic, Australia: Curriculum Corporations.

Bransford, J. D., & Schwartz, D. L. (1999). Rethinking transfer: A simple proposal with multiple implications. In A. Iran-Nejad & P. D. Pearson (Eds.), Review of research in education (pp. 61–101). Washington, DC: American Educational Research Association.

Chazan, D., & Ball, D. (1999). Beyond being told not to tell.For the Learning of Mathematics, 19, 2–10.

Curry, L. A. (2004). The effects of self-explanations of correct and incorrect solutions on algebra problem-solving performance. In K. Forbus, D. Gentner, & T. Regier (Eds.),Proceedings of the 26th annual conference of the cognitive science society (p. 1548). Mahwah, NJ: Erlbaum.

Gentner, D. (2005). The development of relational category knowledge. In D. H. Rakison & L. Gershkoff-Stowe (Eds.),Building object categories in developmental time (pp.245–275). Mahwah, NH: Erlbaum.

Gentner, D. (2010). Bootstrapping the mind: Analogical processes and symbol systems. Cognitive Science, 34, 752–775.

Gick, M. L., & Holyoak, K. J. (1983). Schema induction and analogical transfer. Cognitive Psychology, 15, 1–38.

Gick, M. L., & Paterson, K. (1992). Do contrasting examples facilitate schema acquisition and analogical transfer?Canadian Journal of Psychology, 46, 539–550.

Große, C. S., & Renkl, A. (2006). Effects of multiple solution methods in mathematics learning. Learning and Instruction,16, 122–138.

Große, C. S., & Renkl, A. (2007). Finding and fixing errors in worked examples: Can this foster learning outcomes?Learning and Instruction, 17, 612–634.

Guo, J. P., & Pang, M. F. (2011). Learning a mathematical concept from comparing examples: The importance of variation and prior knowledge. European Journal of Psychology of Education, 26, 495–525.

Guo, J. P., Pang, M. F., Yang, L. Y., & Ding, Y. (2012)Learning from comparing multiple examples: On the dilemma of “similar” or “different”. Educational Psychology Review, 24, 251–269.

Guo, J. P., Yang, L. Y., & Ding, Y. (2014). Effects of example variability and prior knowledge in how students learn to solve equations. European Journal of Psychology of Education, 29, 21–42.

Hammer, R., Bar-Hillel, A., Hertz, T., Weinshall, D., &Hochstein, S. (2008). Comparison processes in category learning: From theory to behavior. Brain Research, 1225,102–118.

Hiebert, J. (1986). Conceptual and procedural knowledge: The case of mathematics. Hillsdale, NJ: Erlbaum.

Holmqvist, M., Gustavsson, L., & Wernberg, A. (2007).Generative learning: Learning beyond the learning situation.Educational Action Research, 15, 181–208.

Holyoak, K. J. (2012). Analogy and relational reasoning. In K.J. Holyoak & R. G. Morrison (Eds.), The Oxford handbook of thinking and reasoning (pp. 234–259). New York:Oxford University Press.

Holyoak, K. J., & Koh, K. (1987). Surface and structural similarity in analogical transfer. Memory & Cognition, 15,332–340.

Kalyuga, S. (2007). Expertise reversal effect and its implications for learner-tailored instruction. Educational Psychology Review, 19, 509–539.

Kalyuga, S., & Renkl, A. (2010). Expertise reversal effect and its instructional implications: Introduction to the special issue. Instructional Science, 38, 209–215.

Ki, W. W. (2007). The enigma of Cantonese tones: How intonation language speakers can be assisted to discern them (Unpublished doctorial dissertation). University of Hong Kong.

Kilpatrick, J., Swafford, J. O., & Findell, B. (Eds.). (2001).Adding it up: Helping children learn mathematics.Washington, DC: National Academy Press.

Lampert, M., & Cobb, P. (2003). Communication and language.In J. Kilpatrick, W. G. Martin & D. Schifter (Eds.), A research companion to principles and standards for school mathematics (pp. 237–249). Reston, VA: National Council of Teachers of Mathematics.

Marton, F., & Booth, S. (1997). Learning and awareness.Mahwah, NJ: Lawrence Erlbaum Associates.

Merrill, M. D., & Tennyson, R. D. (1978). Concept classification and classification errors as a function of relationships between examples and nonexamples. Improving Human Performance Quarterly, 7, 351–364.

Namy, L. L., & Clepper, L. E. (2010). The differing roles of comparison and contrast in children’s categorization.Journal of Experimental Child Psychology, 107, 291–305.

National Council of Teachers of Mathematics. (2000).Principles and standards for school mathematics. Reston,VA: National Council of Teachers of Mathematics.

Ning, N., & Yu, P. (2010). Effects of multiple varied mathematical examples on transfer. Journal of Mathematics Education, 19, 50–52.

[宁宁, 喻平. (2010). 多重变异性数学样例对迁移影响的初步研究. 数学教育学报, 19, 50–52.]

Oakes, L. M., & Ribar, R. J. (2005). A comparison of infants’categorization in paired and successive presentation familiarization tasks. Infancy, 7, 85–98.

Paas, F. G. W. C., & van Merriënboer, J. J. G. (1994).Variability of worked examples and transfer of geometrical problem-solving skills: A cognitive-load approach. Journal of Educational Psychology, 86, 122–133.

Pang, M. F., & Marton, F. (2005). Learning theory as teaching resource: Enhancing students’ understanding of economic concepts. Instructional Science, 33, 159–191.

Quilici, J. L., & Mayer, R. E. (1996). Role of examples in how students learn to categorize statistics word problems.Journal of Educational Psychology, 88, 144–161.

Ranzijn, F. J. A. (1991). The number of video examples and the dispersion of examples as instructional design variables in teaching concepts. The Journal of Experimental Education,59, 320–330.

Reed, S. K. (1989). Constraints on the abstraction of solutions.Journal of Educational Psychology, 81, 532–540.

Renkl, A., Stark, R., Gruber, H., & Mandl, H. (1998). Learning from worked-out examples: The effects of example variability and elicited self-explanations. Contemporary Educational Psychology, 23, 90–108.

Richey, J. E., & Nokes-Malach, T. J. (2013). How much is too much? Learning and motivation effects of adding instructional explanations to worked examples. Learning and Instruction, 25, 104–124.

Richland, L. E., Holyoak, K. J., & Stigler, J. W. (2004).Analogy use in eighth-grade mathematics classrooms.Cognition and Instruction, 22, 37–60.

Richland, L. E., Zur, O., & Holyoak, K. J. (2007). Cognitive supports for analogies in the mathematics classroom.Science, 316, 1128–1129.

Rittle-Johnson, B., & Star, J. R. (2007). Does comparing solution methods facilitate conceptual and procedural knowledge? An experimental study on learning to solve equations. Journal of Educational Psychology, 99, 561–574.

Rittle-Johnson, B., & Star, J. R. (2009). Compared with what?The effects of different comparisons on conceptual knowledge and procedural flexibility for equation solving.Journal of Educational Psychology, 101, 529–544.

Rittle-Johnson, B., Star, J. R., & Durkin, K. (2009). The importance of prior knowledge when comparing examples:Influences on conceptual and procedural knowledge of equation solving. Journal of Educational Psychology, 101,836–852.

Ross, B. H. (1997). The use of categories affects classification.Journal of Memory and Language, 37, 240–267.

Ross, B. H., & Kennedy, P. T. (1990). Generalizing from the use of earlier examples in problem solving. Journal of Experimental Psychology: Learning, Memory, and Cognition,16, 42–55.

Ross, B. H., & Kilbane, M. C. (1997). Effects of principle explanation and superficial similarity on analogical mapping in problem solving. Journal of Experimental Psychology: Learning, Memory, and Cognition, 23, 427–440.

Schwartz, D. L., & Bransford, J. D. (1998). A time for telling.Cognition and Instruction, 16, 475–522.

Schwartz, D. L., & Martin, T. (2004). Inventing to prepare for future learning: The hidden efficiency of encouraging original student production in statistics instruction. Cognition and Instruction, 22, 129–184.

Star, J. R., Pollack, C., Durkin, K., Rittle-Johnson, B., Lynch,K., Newton, K., & Gogolen, C. (2015). Learning from comparison in algebra. Contemporary Educational Psychology,40, 41–54.

Star, J. R., & Rittle-Johnson, B. (2009). It pays to compare: An experimental study on computational estimation. Journal of Experimental Child Psychology, 102, 408–426.

Sweller, J. (2010). Element interactivity and intrinsic, extraneous,and germane cognitive load. Educational Psychology Review,22, 123–138.

Tobias, S. (1989). Another look at research on the adaptation of instruction to students’ characteristics. Educational Psychologist, 24, 213–227.

van Dooren, W., de Bock, D., Hessels, A., Janssens, D., &Verschaffel, L. (2004). Remedying secondary school students’illusion of linearity: A teaching experiment aiming at conceptual change. Learning and Instruction, 14, 485–501.Verschaffel, L., Luwel, K., Torbeyns, J., & van Dooren, W.(2009). Conceptualizing, investigating, and enhancing adaptive expertise in elementary mathematics education.European Journal of Psychology of Education, 24,335–359.

Wittwer, J., & Renkl, A. (2008). Why instructional explanations often do not work: A framework for understanding the effectiveness of instructional explanations. Educational Psychologist, 43, 49–64.

Wittwer, J., & Renkl, A. (2010). How effective are instructional explanations in example-based learning? A meta-analytic review. Educational Psychology Review, 22, 393–409.

Xing, Q., & Mo, L. (2005). The effect of variability and encoding of multiple-examples on transfer. Journal of Psychological Science, 28, 1382–1387.

[刑强, 莫雷. (2005). 多重样例的变异性和编码对迁移影响的实验研究. 心理科学, 28, 1382–1387.]

Yang, L. Y., & Guo, J. P. (2014). The role of variability and prior knowledge in learning from comparing multiple examples. Journal of Psychological Science, 37, 668–677.

[杨凌燕, 郭建鹏. (2014). 多重样例变异性与先前知识对样例学习效果的影响述评. 心理科学, 37, 668–677.]

Zhang, Q., & Zhao, H. (2008). Transfer effects of learning through two varied worked examples on word-problem solving. Acta Psychologica Sinica, 40, 409–417.

[张奇, 赵弘. (2008). 算术应用题二重变异样例学习的迁移效果. 心理学报, 40, 409–417.]