基于属性掌握概率的认知诊断计算机化自适应测验选题策略*

2015-02-06罗照盛喻晓锋高椿雷李喻骏彭亚风王王钰彤

心理学报 2015年5期

罗照盛喻晓锋,2 高椿雷李喻骏彭亚风王睿王钰彤

(1江西师范大学心理学院,南昌 330022) (2亳州师范高等专科学校,亳州 236800)

1 引言

相对于传统的测验形式,计算机化自适应测验(Computerized Adaptive Test,CAT)由于有更高的测试效率和更好的测验精度而受到广泛关注(Barrada,Olea,Ponsoda,&Abad,2008;Chang &Ying,1999;Chang,Qian,&Ying,2001;程小杨,丁树良,严深海,朱隆尹,2011;刘珍,丁树良,林海菁,2008)。与其它测验形式相比,认知诊断(Cognitive Diagnosis,CD)测验最大的优势在于它能提供被试在测验领域上的知识诊断报告,这个诊断报告包含了更加丰富的评价信息,可以对被试的进一步学习、教师开展针对性教学等提供帮助(Leighton&Gierl,2007;Rupp,Templin,&Henson,2010)。

认知诊断计算机化自适应测验(Cognitive Diagnostic Computerized Adaptive Testing,CD-CAT)(Cheng,2009a,2009b;McGlohen&Chang,2008;Xu,Chang,&Douglas,2003)建立在传统CAT(指没有诊断功能的CAT)的基础之上,同时赋予传统CAT新的功效—认知诊断,它是将认知诊断的基本理论、方法与计算机自适应测验相结合的产物。CD-CAT结合了CAT和CD的优点,它一方面可以对被试的知识状态进行诊断;另一方面在诊断过程中可以有针对性、“量体裁衣”式的选择项目让被试作答,从而有利于提高测验效率和测量精度(Cheng,2009a)。根据Wang (2013)的描述,CD-CAT是结合了CD和CAT二者的优点的一种测验,其中CD的目的是根据被试的知识掌握情况对被试分类,找到被试的优势和弱点,而 CAT的算法则使这一过程尽可能更高效的实现。

在传统 CAT研究中,选题策略是一个重要的组成部分,每次都是基于被试的当前能力估计值,根据某种信息测度(比如Fisher最大信息量)来选择下一个要施测的项目,从而达到采用较少的项目估计被试的能力也能达到预先设定的精度(Chang &Ying,1996)。

关于CD-CAT的选题策略,已有的研究主要有5种：一是基于 KL信息量的选题策略(KL),即根据被试的当前属性掌握模式估计值,每次从题库或剩余题库中选择KL信息量最大的项目施测(Cheng,2009a)。二是基于香农熵的选题策略(SHE),根据被试的当前属性掌握模式估计值,每次从题库或剩余题库中选择香农熵最小的项目施测(Tatsuoka,2002,Xu et al.,2003)。三是基于后验概率加权的KL信息量的选题策略(PWKL),相对于 KL信息量选题策略,PWKL给KL信息量增加了不同的权重,权重是属性掌握模式的后验概率(Cheng,2009a)。四是基于后验概率和属性掌握模式距离加权的KL信息量的选题策略(HKL),相对于PWKL选题策略,HKL选题策略的区别在于权重不同,HKL选题策略同时考虑后验概率和属性掌握模式间的相似性来对KL信息量加权(Cheng,2008,2009a)。有关这4种选题策略的详细计算方式,请参考 Cheng (2008,2009a),并且Cheng对这4种选题策略之间的关系进行了阐述和说明。根据Cheng研究结果,这4种选题策略的模式分类准确率最高的是 HKL,并且 PWKL与HKL的模式分类准确率很接近。第五种是基于互信息(Mutual Information)的选题策略(MI,Wang,2013),Wang研究了短测验下,比较 MI与 KL,PWKL,SHE等策略的表现,模拟研究结果表明：对被试的属性掌握模式准确率上,在 Wang的实验条件下,MI在多数情况下略占优。

已有的 CD-CAT选题策略基本是基于被试属性掌握模式的当前估计值,并结合某种信息测度,比如 KL信息量,香农熵或互信息等,从题库或剩余题库中选择某个项目来施测。属性掌握模式估计值通常是通过截断点转换(比如将属性掌握概率与0.5比较,大于0.5则认为被试掌握了某属性,否则不掌握)或者是取最大期望后验概率(Maximum A Posterior,MAP)对应的属性掌握模式而得到(Huebner &Wang,2011)。然而,在自适应测验初期,由于对被试水平的诊断信息较少,此时的属性掌握模式估计值可能存在较大偏差,如果采用的选题策略仅仅基于当前的属性掌握模式和作答,会不利于估计被试的属性掌握模式,进而影响到整个CD-CAT的测验效度和测验精度(涂冬波,蔡艳,戴海崎,2013)。涂冬波等(2013)研究了在初始阶段选择包含“可达矩阵”的项目让被试作答,模拟实验结果表明,初始阶段的选题对被试的属性掌握模式的估计是有影响的。根据被试属性掌握概率和人为给出的截断点赋以被试的知识状态,比如截断点为0.5,则两个知识状态某一个分量(属性掌握概率)为0.01和0.49的,都评判为该属性没有掌握,但是两者的差异是明显的。因此,被试属性掌握概率(Attribute Mastery Probability,AMP)可以更直接地反映被试的当前水平,还未发现基于被试属性掌握概率的选题策略的研究(即在测试过程中,使用属性掌握概率变化加权的选题策略)。也正是基于这种考虑,本研究基于被试的属性掌握概率,提出两种新的选题策略,并与已有的CD-CAT下的选题策略进行比较。

2 基于属性掌握概率的选题策略

在介绍新的选题策略之前,首先对涉及到的概念和符号进行说明。

2.1 相关的概念

属性掌握概率：它是一个由0到1之间的数,被试在测验各属性上的掌握概率就构成了属性掌握概率向量,每个元素对应了被试对该位置上的属性的掌握概率。比如：某被试的属性掌握概率向量为[0.21,0.68,0.85],表明该被试掌握测验中三个属性的概率分别是0.21、0.68和0.85。

属性掌握模式(或称知识状态)：它是一个由 0和1组成的二值向量,其中向量中的0表示被试对该位置对应的属性没有掌握,1表示掌握。比如：某被试的属性掌握模式为[0,1,1],表明测验考察了三个属性,该被试掌握了第2和第3个属性,未掌握第1个属性。属性掌握模式通常是通过属性掌握概率转换得到的,比如采用 0.5为截断点,属性掌握概率为[0.21,0.68,0.85]的被试的属性掌握模式为[0,1,1]。

属性掌握概率变化加权：属性掌握概率变化是指被试在作答某个项目前后其属性掌握概率的差异,分为三种情况：单个属性掌握概率变化、最不确定属性掌握概率变化和属性掌握概率之和的变化。比如被试在作答某项目之前的属性掌握概率为[0.21,0.68,0.85],作答之后其属性掌握概率变为[0.61,0.75,0.91]。单个属性掌握概率变化是作答前后指3个属性的掌握概率变化值,分别为0.40、0.07和0.06,其中第1个属性的掌握概率变化最大;最不确定属性掌握概率是指与0.5最接近的属性掌握概率,比如[0.21,0.68,0.85]中与0.5最接近属性第2个属性,其掌握概率是0.68,在作答之后变为0.75,需要注意的是,这里所说的“最不确定”只是一个相对的概念,它是以概率 0.5作为参照;属性掌握概率之和变化是指作答某项目前后3个属性的掌握概率之和变化的绝对值,作答之前的属性掌握概率之和为0.21+0.68+0.85=1.74,作答之后为0.61+0.75+0.91=2.27,则变化值为 0.53 (可以由|2.27-1.74|=0.53得到)。将属性掌握概率的变化(包括上面的三种情况)值作为选题时的一个权重即为属性掌握概率变化加权。

2.2 相关的符号

2.3 基于属性掌握概率的选题策略

在认知诊断测验中,期望后验估计(Expect A Posterior,EAP)方法常常被用来计算被试在每个属性上的掌握概率(即被试在属性上的边际掌握概率),进一步将被试对属性的掌握概率与 0.5相比较,当属性掌握概率大于 0.5时,即认为被试掌握了该属性,否则认为被试没有掌握该属性 (Huebner &Wang,2011)。基于属性掌握概率的选题策略是从属性掌握概率出发,对属性掌握概率不作 0、1转换,选择对被试属性掌握概率影响最大的项目作为下一个施测的项目。这样做的原因有两个：第一是因为在测验初期,对被试的属性掌握概率估计存在较大的偏差,随着测验的进行,这个属性掌握概率估计值会逐渐趋近其真值,我们希望新的选题策略能使测验加快这个过程,因此选择能使被试的属性掌握概率改变最大的项目作为下一个施测的项目;第二是由于被试的属性掌握模式是通过将属性掌握概率与截断点(通常取 0.5)进行比较,然后转换得到的,但是当一个属性的掌握概率与0.5非常接近,比如0.501或0.499,其实此时测验对该属性的状态“非常不确定”的。模拟实验表明,基于单个属性掌握概率变化最大、基于最不确定属性的掌握概率变化最大的策略表现不佳,因此这里仅考虑研究基于属性掌握概率之和变化最大的策略(即选择作答某项目前后,被试对各属性的掌握概率之和变化最大的项目)的表现。

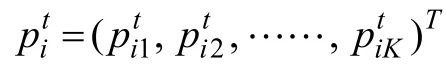
2.3.1 基于后验概率和属性掌握概率变化加权的KL选题策略

记后验概率和属性掌握概率变化加权的KL选题策略为 PPWKL (Posterior Probability Weighted Kullback–Leibler)。PWKL选题策略是基于后验概率加权的KL信息量,这里的PPWKL是在PWKL的基础上,增加了属性掌握概率的变化值这一权重,即基于后验概率和属性掌握概率变化加权的KL信息量。PPWKL指标的计算方式为

该选题策略可以表示为：

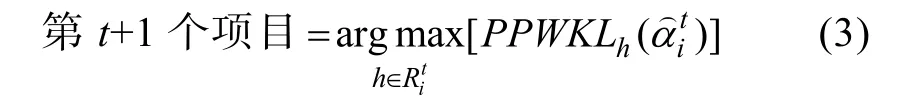
2.3.2 基于后验概率、属性掌握概率变化和属性掌握模式距离加权的KL选题策略

记后验概率、属性掌握概率变化和属性掌握模式距离加权的 KL选题策略为 PHKL(Posterior HybridKullback–Leibler)。与 PPWKL 不同,这里的PHKL是在HKL的基础上,增加了属性掌握概率之和的变化值这一权重,即基于后验概率、属性掌握概率变化和属性掌握模式距离加权的KL信息量。PHKL指标的计算方式为

该选题策略可以表示为：

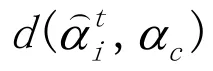
3 模拟研究1

3.1 研究设计

为了考察基于属性掌握概率的选题策略的表现,考虑基于 DINA模型,模拟定长和变长的CD-CAT测验。已有的研究中,CD-CAT的测验长度经常取12到24这个范围(陈平等,2011;涂冬波等,2013;Wang,2013)。本研究中,对于定长的CD-CAT测验,测验长度采用16。对于变长的CD-CAT测验,终止规则由测验长度和属性掌握模式后验概率确定,只要二者之一达到预先设定的值即终止测验。Hsu,Wang和Chen (2013)研究了变长CD-CAT下,属性掌握模式后验概率取不同值对测验长度、测验精度的影响,Hsu等的结果表明,对于高风险和低风险的测验,属性掌握模式后验概率分别应取不低于0.9和不高于0.8。考虑的测验长度(每位被试测验的最大长度)也是 16,属性掌握模式后验概率最大值固定为0.8(Hsu et al.,2013;Tatsuoka,2002),即测验长度达到最大值或者属性掌握模式后验概率达到最大值时结束测验。

目前多数的CD-CAT研究是基于4-8个属性进行的,其中 6个居多(Cheng,2009a,2010;Wang,Chang,&Huebner,2011;Xu et al.,2003),这里模拟的题库考虑6个属性。

题库中各项目的属性向量和项目参数,被试属性掌握模式的模拟按如下方式进行：

(1) 题库中的项目数固定为200,各项目按0.2的概率考察每个属性,并且保证每个项目至少考察1个属性,最多考察3个属性(Henson,2004);

(2) 项目参数

和

都采用均匀分布,取值区间为[0.05,0.25];

(3) 因为在实际的测验情境下,所考察的属性之间可能存在相关。为了比较不同情况下,各策略的表现,分别考虑属性间独立和属性间存在相关的情况。对于属性间相互独立的情况,假设被试掌握每个属性的概率服从参数为 0.5的 Bernoulli分布,随机生成被试的属性掌握情况。对于属性间存在相关的情况,这里分别取0.2,0.35,0.5,0.6,0.7,0.8共6种情况的相关,比如 0.2表示所有属性之间存在0.2左右(表示属性间的相关接近 0.2,可能不一定刚好是 0.2)的相关,其它相关的含义与此相同。模拟属性间的相关可以通过HO-DINA模型的高阶参数来控制,可以模拟被试总体对掌握的各属性之间存在不同大小的相关,具体可以参考Wang,Chang和 Douglas (2012)。这样一来,就存在属性间相互独立,属性之间存在较低的相关(相关系数为 0.2和0.35),中等程度的相关(相关系数为0.5和0.6)和较高的相关(相关系数为0.7和0.8)共7种情况。

一共模拟1000名被试,200个项目,有7种被试总体(指属性之间独立和存在不同的相关)。基于各选题策略模拟 CD-CAT。每种选题策略重复 20次,结果取平均值,所有的模拟程序采用Java语言编制。

3.2 CD-CAT测验施测过程

CD-CAT按如下过程进行模拟：(1)随机生成被试的属性掌握模式;(2)按采用的选题策略,选择下一个要施测的项目;(3)模拟被试作答;(4)采用EAP方法估计被试的属性掌握概率(de la Torre,2009)。对于涉及到KL信息量的选题策略,还需估计被试的属性掌握模式,Huebner和Wang (2011)的研究表明,采用MAP方法估计被试的属性掌握模式更好,因此,这里采用 MAP方法估计被试的属性掌握模式;(5)转到步骤(2),直到满足测验终止规则。当所有的被试完成测验后,计算相应的评价指标。

3.3 评价指标

为了能全面地比较不同选题策略之间的差异,综合考虑各评价指标下不同选题策略的表现,采用统一量纲再加权求和的方法,具体做法是：对值越大越好的指标,将该评价指标上的最大值做分母,把各选题策略在该指标上的值做分子,求两者的比值;对值越小越好的指标,则将评价指标上的最小值作为分子,把各选题策略在该指标上的值作为分母,求两者的比值。统一量纲后,对某选题策略的10个评价指标比值分别赋加权系数。加权求和值最大的,则该选题策略在各个方面的综合效果最好;反之则最差(陈德枝,2004;刘珍等,2008;)。本文中所采用的10个评价指标中有2个(PMR,MMR)是评价测验的估计精度,余下的8个是评价测验题库使用相关的指标,因此,为了使两类指标(评价知识状态准确性的指标和评价题库使用均匀性的指标)在统一量纲中占有相同的比重,加权系数的设置方式为：PMR和MMR指标的权重设置为4,其余指标的权重设置为 1,这样可以保证两类指标占有相同的比重。这里举一个例子说明,比如表1中,对于 PHKL的统一量纲的指标计算方式为：4×0.961/0.961+4×0.992/0.992+1×16/16+1×92.118/9 3.357+1×0.540/0.546+1×1+1×0.967/0.972+1×1+1×9 8/100+1×22/25=15.83,其中对 PMR和 MMR来说是值越大越好,计算时是将各策略对应的指标作为分子,所有PMR和MMR中最大的值作为分母,并且乘上对应的权重;其它指标是越小越好,计算时是将各策略对应的指标作为分母,所有对应指标中最小值作为分子,并且乘上相应的权重,最后对所有指标按统一量纲后求和,得到评价各策略的综合评价指标。

3.4 实验结果

3.4.1 属性之间独立时的结果

表1和表2分别对应了定长和变长CD-CAT测验下各评价指标的值,并且表1和表2中的最后一列分别对应了定长和变长 CD-CAT测验下各选题策略的综合评价指标。

表1 各选题策略的分类准确率和题库使用均匀性(定长,属性独立)

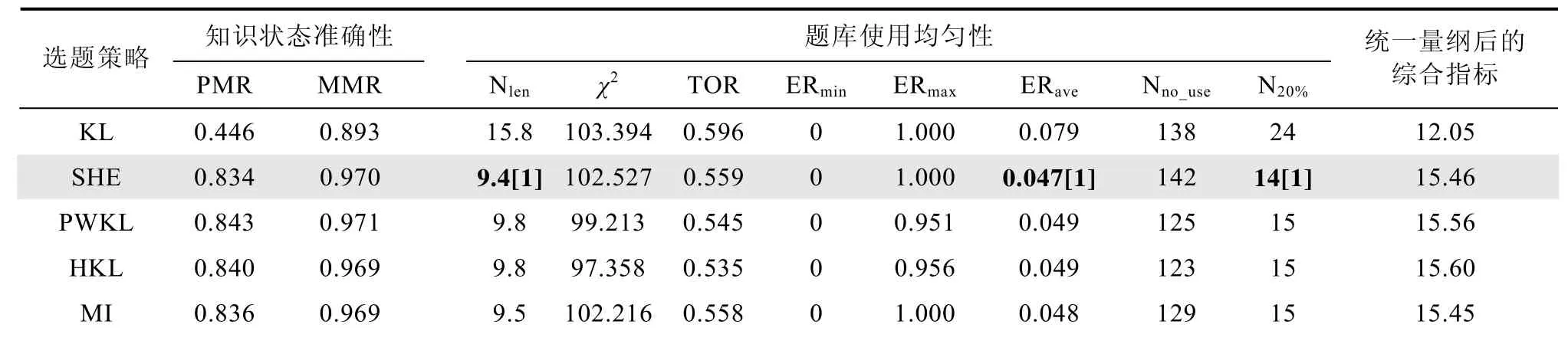
表2 各选题策略的分类准确率和题库使用均匀性(变长,属性独立)

PPWKL 0.840 0.969 9.8 94.621 0.522 0 0.948 0.049 121 16 15.61

根据表1和表2,在测验长度为16的定长CDCAT下,如果考察测验的精度,则 PHKL,MI和PPWKL的表现较好,分别排名前三位。如果综合测验精度和题库的使用均匀性指标,则 PPWKL,PHKL和MI表现略好。在变长(最大测验长度为16,最大后验概率为0.8)的CD-CAT下,PHKL,PWKL,PPWKL和HKL的测验对被试的知识状态估计精度较好,PHKL和PPWKL在题库使用均匀性的表现占优。

总的来说,在属性独立情况下,无论是定长,还是变长的 CD-CAT,考虑了属性掌握概率的选题策略在保证测验精度不损失或损失较小的情况下,在题库使用均匀性上的表现都更好,这些都可以从表1和表2可以很明显的看出来。

3.4.2 属性之间存在相关时的结果

表3和表4对应了属性之间存在较低的相关,定长和变长CD-CAT测验各评价指标的值。

从表3可以看出,在属性之间存在低相关,长度为 16的定长 CD-CAT下,单从测验精度来看,PHKL和SHE略占优势,其中PHKL选题策略的测验精度最好,排在2,3,4位的分别是SHE,MI和PPWKL,它们与PHKL选题策略与PMR指标分别相差 1%,1.5%和 1.5%;但是如果考察题库的使用均匀性指标,PHKL选题策略最好,有4项指标(分别是

,TOR,ER,N)排名第一,1项指标(N)排名第二,剩下的三项指标(N,ER和ER)都相同。综合测验精度和题库的使用均匀性来看,PHKL的表现较好,这一点从统一量纲后的综合指标也能看出。综合指标排在前三位的分别是PHKL、PPWKL和HKL。属性间存在中等相关和较高相关时的详细结果请参考附录二。PHKL在属性之间存在中等相关,长度为 16的定长 CD-CAT下有 6项指标排名第1(分别是 PMR,MMR,

,TOR,ER,N)。从测验精度来说,PHKL和MI很接近,分别排在前2位,但是PHKL在题库使用均匀性上有很大优势,附录二表6中的综合指标也表明PHKL策略的综合表现更好。当属性之间存在高相关,长度为 16的定长CD-CAT下,在测验精度指标上,MI策略最好(其PMR和MMR指标都排第1),但是从题库使用上来看,PHKL策略更好(

,TOR,ER,N指标都排在第1位),详细结果请参考附录二中的表7。综合来看,PHKL策略略占优。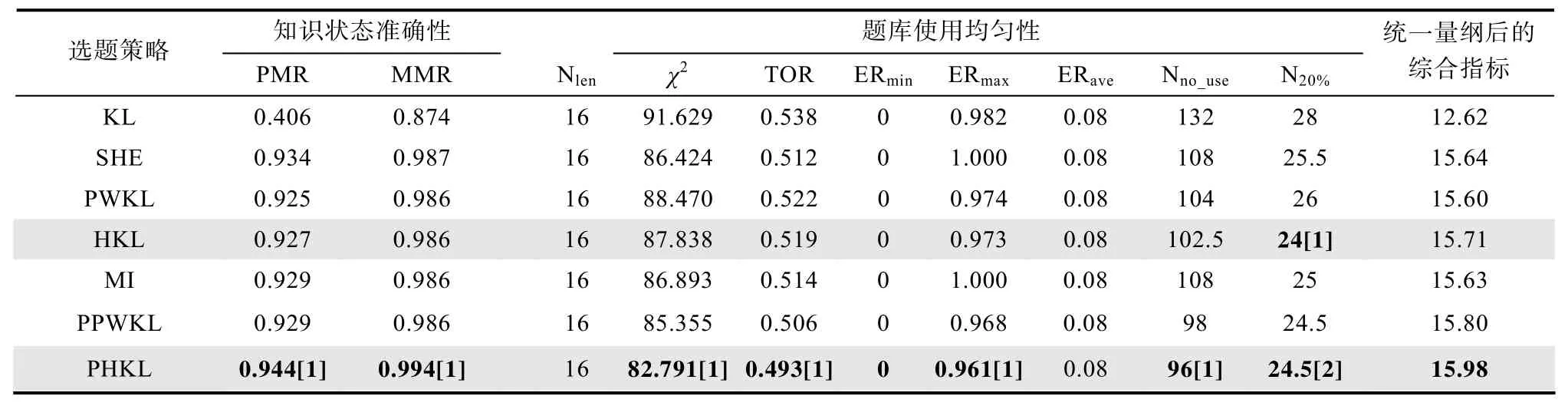

表3 各选题策略的分类准确率和题库使用均匀性(定长,低相关)

表4 各选题策略的分类准确率和题库使用均匀性(变长,低相关)

表4的结果来看,在属性间存较低相关,最大测验长度为16,后验属性掌握模式概率为0.8的变长CD-CAT下,单从测验精度来看,PHKL、PWKL和SHE的表现较好,分别处于第1、2和3位。综合来看,PHKL,PPWKL和MI选题策略的总体表现较好,分别有4,3和3项指标排名第一,PHKL的综合指标表现最好,这说明在考虑了被试的属性掌握概率变化之后,在保证测验精度的同时,对题库使用的均匀性控制上也有了改善。

属性间存在中等相关和较高相关时也有类似的结论,详细结果请参考附录三中的表8和表9。

总体来说,在变长 CD-CAT下,考虑了属性掌握概率的选题策略 PHKL,在测验精度和题库使用均匀性指标上表现都较好,无论是属性之间存在较低相关、中等相关或是较高相关的情况,PHKL的综合指标都排在第1位。

4 模拟研究2

认知诊断测验可能会用于日常分项诊断中,比如单元测验、随堂诊断测验等,此时,题目量可能会比较少。为了考察不同题量情形下各种选题策略的表现,选取PWKL、HKL、MI、PPWKL和PHKL五个选题策略。考虑属性之间相互独立、存在相关时,它们在短测验下的表现。所有的数据模拟方式与研究1相同,不同的是本研究中考察的是长度分别为4、6、8和10的定长测验,即模拟4种短测验,考察这5种选题策略的表现。所采用的评价指标与研究1相同。表5列出了属性独立时,4种选题策略在4种定长的短测验中的表现。

从表5的结果可以看出,在属性相互独立时,所列出的所有短测验(也可以看作是长测验的测验初期)中,大部分情况下,PHKL的各项指标都是最好的。从统一量纲后的综合指标来看,PHKL几乎总是优于其它几种策略,只有在测验长度为 10时,PPWKL综合指标指第 1位。总的来说,考虑了属性掌握概率的选题策略 PHKL和 PPWKL,在综合测验精度和题库使用均匀性指标后略占优势。

当属性之间存在较低、中等和较高相关时,各选题策略在短测验中的表现,请参考附录4中的表10,11和12。从表10,11和12可以看出,PHKL和MI两中策略的测验精度几乎总是排在前两位,在长度为4和6的测验中,PHKL占优,在长度为8和10的测验中,MI占优,并且当属性之间的相关达到中等以上时,MI在测验精度上的优势比属性之间存在低相关时略大;在大多数情况下,PHKL和PPWKL在题库使用均匀性上的表现总是排在前 2位。综合来看,PHKL大多数情况下,综合指标都是排在第1位。

表5 三种选题策略的分类准确率和题库使用均匀性(短测验,属性独立)

PPWKL 0.804 0.958 99.320 0.546 0 0.955 0.050 133 15 15.903 MI 0.806 0.959 106.431 0.582 0 1.000 0.050 151 16 15.566

5 小结与讨论

通过对基于属性掌握概率的2种选题策略与5种已有的CD-CAT下的选题策略的比较研究发现：在属性之间是独立的定长和变长的CD-CAT中,考虑了属性掌握概率的PHKL和PPWKL选题策略在测验精度和题库的利用率上的综合表现优于其它选题策略;当属性之间存在较低、中等和较高相关时,在定长和变长的CD-CAT中,PHKL和PPWKL在保证测验精度的同时,对题库使用的均匀性控制上也有了改善,它们的综合指标排在前 2位;当属性之间存在较低、中等和较高相关的短测验中,在测验长度为4和6时,PHKL的测验精度更好,当测验长度达到8和10时,MI的测验精度更好,这说明PHKL策略更适合在测验初期使用;PHKL和PPWKL策略的一大优点是在不损失或较少损失测验精度的条件下,能改善题库的使用均匀性。

在测验初期,因为关于被试属性掌握状态的信息较少,采用基于属性掌握模式的选题策略可能不利于对被试的知识状态的估计,因为这人为增加了误差。特别是在测验长度较短时,从表10,11和12中的结果很清楚地说明了这一点,基于属性掌握概率的PHKL和PPWKL,以及基于互信息的MI的测验精度分别排在前3位。PHKL和PPWKL选题策略在选题时考虑了属性掌握模式的后验概率和被试的属性掌握概率的变化情况,选题时一方面考虑被试的总体分布情况,另一方面也考虑了所选择的项目对于被试属性掌握概率的影响,越能改变被试属性掌握概率的项目越容易被选到,这样在测验长度较短时就有利于估计被试的属性掌握模式。

基于属性掌握概率的选题策略与基于属性掌握模式的选题策略的不同之处在于前者考虑了被试的属性掌握概率变化情况,而后者只考虑被试的属性掌握模式估计值。被试的属性掌握概率是在区间0到1之间的连续值,被试作答每个题之后,都会引起其属性掌握概率的变化,因此,在选题时将这个变化考虑进去比仅考虑属性掌握模式的变化更精细,特别是在测验长度较短的测验中,因为此时被试的属性掌握模式估计并不准确,此时需要结合更多有用的信息来选题(这一点类似于CAT中的全局信息量选题,可参考Chang和Ying (1996)),有利于提高测验的估计精度,并且考虑了被试的属性掌握概率之后,会对题库的使用均匀性有改善。

在本研究中没有考虑属性之间可能存在的层级关系(hierarchical relationship,可参见 Leighton,Gierl,&Hunka,2004),但在实际的测验中,属性之间有可能会存在层级关系。当属性之间存在层级关系时,特别是很多实际测验中都涉及到的层级关系,PHKL,PPWKL,PWKL,HKL和MI等策略的表现会是什么样的,这需要进一步的深入研究。并且,在实际的应用中,需要根据测验的目的进行综合权衡,选择合适的选题策略。

题库总体利用率较低是所涉及的各种选题策略都存在的问题,这一点从陈平等(2011)的研究结果中也可以得到验证。就本研究来说,在变长CD-CAT测验下,未使用的项目数大多都大于110,也就是说,题库中有超过一半以上的项目都没有被使用到,只是使用了不到一半的项目,这充分反映了这里所使用的选题策略在题库的利用率上的表现还有待进一步提高。

Barrada,J.R.,Olea,J.,Ponsoda,V.,&Abad,F.J.(2008).Incorporating randomness in the Fisher information for improving item-exposure control in CATs.

British Journal of Mathematical and Statistical Psychology,61

,493–513.Chang,H.H.,Qian,J.H.,&Ying,Z.L.(2001).A-stratified multistage computerized adaptive testing with b blocking.

Applied Psychological Measurement,25

(4),333–341.Chang,H.H.,&Ying,Z.L.(1996).A global information approach to computerized adaptive testing.

Applied Psychological Measurement,20

(3),213–229.Chang,H.H.,&Ying,Z.L.(1999).A-stratified multistage computerized adaptive testing.

Applied Psychological Measurement,23

(3),211–222.Chen,P.,Li,Z.,&Xin,T.(2011).A note on the uniformity of item bank usage in cognitive diagnostic computerized adaptive testing.

Studies of Psychology and Behavior,9

(2),125–132.[陈平,李珍,辛涛.(2011).认知诊断计算机化自适应测验的题库使用均匀性初探.

心理与行为研究,9

(2),125–132.]Chen,D.Z.(2004).

Comparison study of item selection strategies of computerized adaptive testing with the Samejima Graded Response Model

(Unpublished Master’s thesis).Jiangxi Normal University.[陈德枝.(2004).

Samejima等级反应模型下CAT选题策略比较研究

(硕士学位论文).江西师范大学.]Cheng,X.Y.,Ding,S.L.,Yan,S.H.,&Zhu,L.Y.(2011).New item selection criteria of computerized adaptive testing with exposure-control factor.

Acta Psychologica Sinica,43

(2),203–212.[程小杨,丁树良,严深海,朱隆尹.(2011).引入曝光因子的计算机化自适应测验选题策略.

心理学报,43

(2),203–212.]Cheng,Y.(2008).

Computerized adaptive testing:new development and applications

(Unpublished doctoral dissertation).University of Illinois at Urbana-Champaign.Cheng,Y.(2009a).When cognitive diagnosis meets computerized adaptive testing:CD-CAT.

Psychometrika,74

(4),619–632.Cheng,Y.(2009b).

Computerized adaptive testing for cognitive diagnosis

.Paper presented at the 2009 GMAC Conference on Computerized Adaptive Testing.Cheng,Y.(2010).Improving cognitive diagnostic computerized adaptive testing by balancing attribute coverge:The modified maximum global discrimination index method.

Educational and Psychological Measurement,70

(6),902–913.de la Torre,J.(2009).DINA model and parameter estimation:A didactic.

Journal of Educational and Behavioral Statistics,34

(1),115–130.Henson,R.A.(2004).

Test discrimination and test construction for cognitive diagnostic models

(Unpublished doctoral dissertation).University of Illinois at Urbana-Champaign

Hsu,C.L.,Wang,W.C.,&Chen,S.Y.(2013).Variable-length computerized adaptive testing based on cognitive diagnosis models.

Applied Psychological Measurement,37

(7),563–582.Huebner,A.,&Wang,C.(2011).A note on comparing examinee classification methods for cognitive diagnosis models.

Educational and Psychological Measurement,71

(2),407–419.Leighton,J.P.,&Gierl,M.J.(2007).

Cognitive diagnostic assessment for education:Theory and applications

.New York:Cambridge University Press.Leighton,J.P.,Gierl,M.J.,&Hunka,S.M.(2004).The attribute hierarchy method for cognitive assessment:A variation on Tatsuoka's rule-space approach.

Journal of Educational Measurement,41

(3),205–237.Liu,Z.,Ding,S.L.,&Lin,H.J.(2008).Item selection strategies for computerized adaptive testing with the generalized partial credit model.

Acta Psychologica Sinica,40

(5),618–625.[刘珍,丁树良,林海菁.(2008).基于GPCM的计算机自适应测验选题策略比较.

心理学报,40

(5),618–625.]McGlohen,M.,&Chang,H.H.(2008).Combining computer adaptive testing technology with cognitively diagnostic assessment.

Behavior Research Methods,40

(3),808–821.Rupp,A.A.,Templin,J.,&Henson,R.(2010).

Diagnostic measurement:Theory,methods and applications

.New York:Guilford.Tatsuoka,C.(2002).Data analytic methods for latent parially ordered classification models.

Journal of the Royal Statistical Society:Series C (Applied Statistics),51

(3),337–350.Tu,D.B.,Cai,Y.,&Dai,H.Q.(2013).Item selection strategies and initial items selection methods of CD-CAT.